Гашков С.Б. Современная элементарная алгебра в задачах и решениях
Подождите немного. Документ загружается.


§ 4.19. Построения циркулем и линейкой 311
Введем понятие сложности построения циркулем и линейкой. Допу
-
стим, что на плоскости дано некоторое множество точек, прямых и окруж
-
ностей, которое обозначим M
0
.
Определение 118. Назовем построением циркулем и линейкой
при заданном M
0
любую последовательность множеств M
0
, M
1
, ..., M
L
,
начинающуюся с M
0
и такую, что каждое следующее множество M
i+1
получается из предыдущего множества M
i
добавлением либо некоторой
прямой, проходящей через какие
-
то две точки из множества M
i
, либо
окружности с центром в какой
-
то из точек множества M
i
и радиусом,
равным длине некоторого отрезка с концами в точках из M
i
, а также
всех точек пересечения добавленной линии со всеми линиями из множе
-
ства M
i
. Число L назовем сложностью этого построения. Сложностью
построения множества M точек, отрезков, окружностей и прямых при
заданном M
0
назовем минимальную сложность такого построения M
0
,
M
1
, .. ., M
L
, для которого множество M
L
содержит все прямые и окруж
-
ности из M, все точки из M и концы всех отрезков из M.
Аналогично определяется сложность построения одним циркулем.
Следующие несколько задач принадлежат итальянскому математику
Маскерони *.
Задачи Маскерони
1. Дана единичная окружность с диаметром и отрезок длины x, x < 1.
Постройте на этом диаметре отрезок длины x
2
одним циркулем со слож
-
ностью 2.
2. Решите предыдущую задачу со сложностью 3, если диаметр задан
только одним своим концом, а не начерчен целиком.
3. Дана единичная окружность и отрезок длины x > 1 c началом в ее
центре. Постройте отрезок длины x
−1
одним циркулем со сложностью 2.
Постройте отрезок длины x
−1
одним циркулем со сложностью 3, если
отрезок длины x задан только своими концами, а не начерчен целиком.
4. Даны отрезки с длинами a, b, c, где b, c < 2a. Постройте одним
циркулем со сложностью 3 отрезок длины x такой, что a : b = c : x.
5. Даны единичная окружность, отрезок длины c < 2 с началом в ее
центре и еще отрезок длины b < 1. Постройте одним циркулем со слож
-
ностью 2 отрезок длины bc.
6. Постройте одним циркулем со сложностью 3 одновременно отрезки
длины 2 и 3, лежащие на одной прямой с данным единичным отрезком.
* Л. Маскерони (Lorenzo Mascheroni, 1750
–
1800). Свою книгу
«
Геометрия циркуля
»
он
посвятил Наполеону.

312 Глава IV. Алгебраические уравнения
7. Поделите пополам отрезок одним циркулем:
а) со сложностью 4, если дана прямая, на которой лежит отрезок,
б) со сложностью 5, если дан только сам отрезок,
в) со сложностью 6, если даны только его концы.
8. Поделите на три равные части отрезок одним циркулем:
а) со сложностью 5, если дана прямая, на которой лежит отрезок,
б) со сложностью 8, если дан только сам отрезок,
в) со сложностью 11, если даны только его концы.
9. Разделите циркулем и линейкой отрезок пополам со сложностью 3
и на четыре равные части со сложностью 6.
10. Разделите циркулем и линейкой отрезок на шесть равных частей
со сложностью 8.
11. Проведите через точку вне прямой параллельную ей прямую
со сложностью 3.
12. На сторонах угла отложены от его вершины отрезки длины a, b и 1
(два из них
––
на одной стороне, а один
––
на другой). Постройте со слож
-
ностью 3 отрезок длины ab на одной из сторон угла.
Следующий цикл задач принадлежит датскому математику Мору *.
Задачи Мора
1. Постройте со сложностью 5 одним циркулем одновременно отрезки
длины
√
a
2
−b
2
, 2
√
a
2
−b
2
, 2b, 3b,
√
3b, если отрезки a и b, a > b, за
-
даны.
2. Постройте со сложностью 5 одним циркулем одновременно отрезки
длины
√
2a,
√
3a,
√
8a, 2a, 3a, если отрезок длины a задан.
3. Постройте со сложностью 11 одним циркулем одновременно от
-
резки длины
√
a
2
+ b
2
, 2
√
a
2
+ b
2
,
√
a
2
−b
2
, 2
√
a
2
−b
2
,
√
2a,
√
3a,
√
8a,
2a, 3a, 2b, 3b,
√
3b, если отрезки a и b, a > b, заданы.
4. Постройте со сложностью 15 одним циркулем одновременно от
-
резки длины a + b, a −b, ab
/
√
a
2
+ b
2
,
√
a
2
+ b
2
, 2
√
a
2
+ b
2
,
√
a
2
−b
2
,
2
√
a
2
−b
2
,
√
2a,
√
3a,
√
8a, 2a, 3a, 2b, 3b,
√
3b, если отрезки a и b, a > b,
заданы.
5. Если отрезки длины a и b заданы на одной прямой, то отрезок
длины a + b можно построить одним циркулем со сложностью 2.
6. Даны отрезки длины 1 и a < 1 с общим концом, вложенные один
в другой. Постройте со сложностью 7 одним циркулем отрезок длины
√
a.
* Г. Мор (George Mohr, 1640
–
1697). В написанной им книге
«
Датский Евклид
»
он
на столетие раньше Маскерони доказал возможность проведения всех геометрических по
-
строений одним лишь циркулем.
§ 4.20. Теорема Абеля
––
Руффини 313
В случае a > 1 подобное построение можно осуществить со сложно
-
стью 9.
7
∗∗
. Докажите теорему Мора
––
Маскерони о построениях одним цир
-
кулем: любое построение, выполнимое циркулем и линейкой, может быть
выполнено и одним циркулем.
§ 4.20. Теорема Абеля
––
Руффини
Теорема 119. Общее уравнение степени выше пятой неразре-
шимо в радикалах, т. е. не существует формулы, выражающей его
корни через коэффициенты, в которой бы кроме четырех арифме-
тических операций использовалось бы только извлечение комплекс-
ных корней произвольных степеней.
Д о к а з а т е л ь с т в о. Прежде всего заметим, что теорему доста
-
точно доказать для общего уравнения пятой степени. В самом деле,
если бы имелась общая формула для решения уравнения n
-
й степени,
то она бы давала решение в радикалах и для уравнения:
x
n
+ a
n−1
x
n−1
+ a
n−2
x
n−2
+ a
n−3
x
n−3
+ a
n−4
x
n−4
+ a
n−5
x
n−5
= 0.
Предположим, что общее уравнение пятой степени
x
5
+ a
4
x
4
+ a
3
x
3
+ a
2
x
4
+ a
1
x + a
0
= 0
имеет решение в радикалах. Для того чтобы дать удобную для наших
целей переформулировку, введем понятие радикального расширения
K
n
√
a
поля K (a ∈K).
Обозначим через K
n
√
a
множество всех выражений вида f
n
√
a
,
где f
––
рациональная функция с коэффициентами из поля K, а элемент
n
√
a удовлетворяет соотношению
n
√
a
n
= a.
Если поле K
––
поле всех рациональных функций, то с элементом
n
√
a
поля K(
n
√
a) тоже можно связать некоторую функцию. Однако строгое
обоснование этого приводит к понятию римановой поверхности, которое
не является элементарным. Мы будем выбирать одно значение корня
n
√
a
и не вдаваться в технические детали. Отметим, что формула, доставля
-
ющая решения уравнения, лежит в поле функций, которое получается
радикальными расширениями из поля рациональных функций.
Рассмотрим некоторые примеры.
Для общего уравнения второй степени x
2
+ a
1
x + a
0
= 0 формула для
решений лежит в поле K
√
a
2
1
−4a
0
, которое совпадает с полем всех
рациональных функций от переменных x
1
и x
2
, для которых x
1
+ x
2
= −a
1
,
x
1
x
2
= a
0
.

314 Глава IV. Алгебраические уравнения
В общем случае, формула для решения уравнения n
-
й степени достав
-
ляла бы последовательность радикальных расширений, которая бы начи
-
налась с поля K
0
= C(a
0
, a
1
, . . ., a
4
) всех рациональных функций, а закан
-
чивалась бы полем всех рациональных функций K
n
= C(x
1
, x
2
, x
3
, x
4
, x
5
)
или некоторым его расширением.
K
0
⊂K
1
⊂K
2
⊂... ⊂K
n
.
При этом поле K
0
выделялось бы в K
n
как множество всех симмет
-
рических рациональных функций, т. к. по теореме Виета a
i
= −σ
i
(x
1
, x
2
,
x
3
, x
4
, x
5
), 0 6 i 6 4, а всякая симметрическая рациональная функция
выражается через элементарные симметрические функции как рацио
-
нальная дробь от них.
Интересен вопрос: можем ли мы прийти к некоторому расширению
поля C(x
1
, x
2
, x
3
, x
4
, x
5
) при последовательном радикальном расширении
поля K
0
по формулам, выражающим x
i
через a
0
, ..., a
4
? Ответ на этот
вопрос отрицательный. Мы дадим здесь только эскиз доказательства.
Рассмотрим вначале пример расширения, соответствующего формулам
Кардано. Пусть дано общее уравнение третьей степени
x
3
+ a
2
x
2
+ a
1
x + a
0
= 0.
Замена переменных x →x + a
2
/
3 приводит его к виду x
3
+ ax + b = 0.
Тогда резольвенты Лагранжа ρ
1
=x
1
+εx
2
+ε
2
x
3
и ρ
2
= x
1
+ ε
2
x
2
+ εx
3
,
где ε = −
1
2
+
√
3
2
i, удовлетворяют условиям:
ρ
1
·ρ
2
= x
2
1
+ x
2
2
+ x
2
3
−x
1
x
2
−x
2
x
3
−x
3
x
1
=
= (x
1
+ x
2
+ x
3
)
2
−3(x
1
x
2
+ x
2
x
3
+ x
3
x
1
) = −3a,
ρ
3
1
+ ρ
3
2
= (ρ
1
+ ρ
2
) [(ρ
1
+ ρ
2
)
2
−3ρ
1
ρ
2
] = 3x
1
[9x
2
1
+ 9a] =
= 27(x
3
1
+ ax
1
) = −27b,
ρ
3
1
−ρ
3
2
= (ρ
1
−ρ
2
)(ρ
2
1
+ρ
1
ρ
2
+ρ
2
2
) =
=
√
3(x
2
−x
3
)(x
2
1
+ε
2
x
2
2
+εx
2
3
+x
2
1
+εx
2
2
+ε
2
x
2
3
+2εx
1
x
2
+ε
2
x
1
x
3
+
+2x
2
x
3
+2ε
2
x
1
x
2
+2εx
1
x
3
+2x
2
x
3
+x
2
1
+x
2
2
+x
2
3
−x
1
x
2
−x
2
x
3
−x
3
x
1
) =
=i
√
3(x
2
−x
3
)(3x
2
1
−3x
1
x
2
−3x
1
x
3
+3x
2
x
3
) =
= i
√
27(x
1
−x
3
)(x
2
−x
3
)(x
1
−x
2
).
Поэтому
(ρ
3
1
−ρ
3
2
)
2
= −27(x
1
−x
2
)
2
(x
2
−x
3
)
2
(x
3
−x
1
)
2
= 27(4a
3
+ 27b
2
).
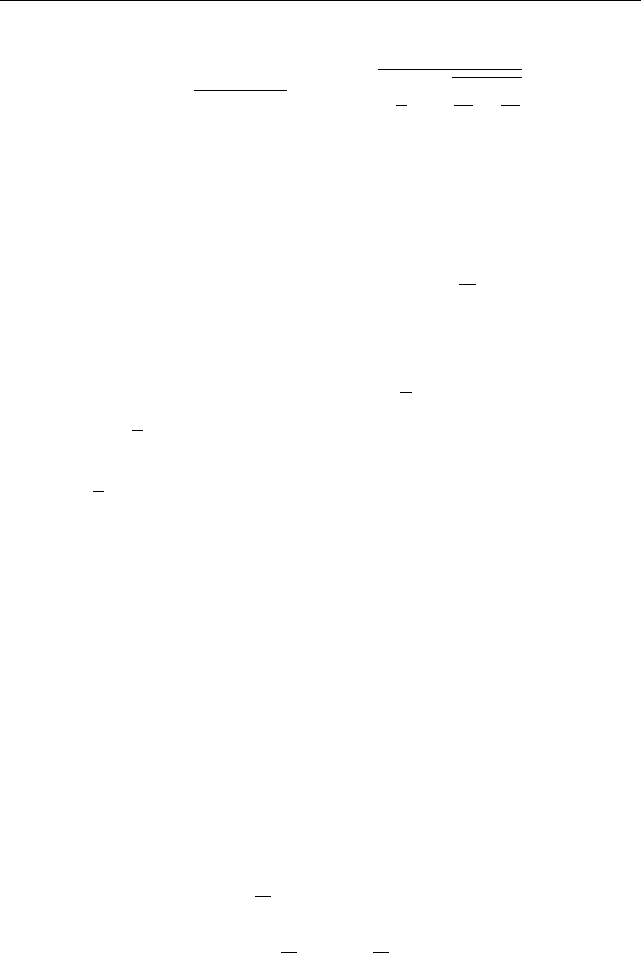
§ 4.20. Теорема Абеля
––
Руффини 315
Значит, можно выбрать следующую цепочку радикальных расши
-
рений:
K
0
⊂K
0
p
4a
3
+ 27b
2
⊂K
0
3
s
−
b
2
+
r
a
3
27
+
b
2
4
!
.
Заметим, что последнее поле совпадает с полем C(x
1
, x
2
, x
3
).
Аналогично можно поступить и с уравнением четвертой степени.
Пусть удалось проделать аналогичные выкладки и для общего урав
-
нения пятой степени, и имеется цепочка радикальных расширений:
C(a
0
, a
1
, a
2
, a
3
, a
4
) = K
0
⊂K
1
⊂... ⊂K
n
= C(x
1
, x
2
, x
3
, x
4
, x
5
).
Лемма 30. Справедливо равенство K
1
= K
0
√
D
, где
D = (x
1
−x
2
)
2
(x
1
−x
3
)
2
... (x
4
−x
5
)
2
––
дискриминант уравнения пятой степени.
Д о к а з а т е л ь с т в о. Пусть K
1
= K
0
r
√
a
и a ∈K
0
, r > 2 и
r
√
a = f(x
1
, x
2
, x
3
, x
4
, x
5
) ∈C(x
1
, x
2
, x
3
, x
4
, x
5
).
Тогда для всякой перестановки α ∈S
5
имеет место равенство αf = ε
α
f,
где ε
α
∈
r
√
a, а αf
––
функция f с переставленными в соответствии с пе
-
рестановкой α переменными.
Действительно, (α f)
r
= α(f
r
) = αa = a = f
r
, так как a ∈C(σ
0
, σ
1
, ...
... , σ
4
) (мы воспользовались свойством перестановки переменных
α(h
1
·h
2
) = αh
1
·αh
2
). Кроме того, для любой функции h выполняет
-
ся свойство αβ (h) = α(βh), из которого вытекает тождество ε
αβ
= ε
α
·ε
β
для α, β ∈S
5
и тождеств
αβ (h) = ε
αβ
h, α(βh) = α(ε
β
h) = ε
β
(αh) = ε
β
·ε
α
h.
Как известно, всякую перестановку можно представить в виде ком
-
позиции транспозиций. Заметим, что ε
(i j)
= ±1, так как (i j) · (i j)
––
тожде
-
ственная перестановка.
Легко видеть, что для любых двух перестановок (i
′
j
′
) и (ij) вы
-
полняется тождество (i
′
j
′
) = (ii
′
)(jj
′
)(ij)(j j
′
)(ii
′
). Отсюда имеем, что
ε
(i j)
= ε
(i
′
j
′
)
. Поэтому, если расширение нетривиальное, то ε
(i j)
= −1 для
всех транспозиций (ij) ∈S
5
. Значит, ε
α
совпадает со знаком ε(α) пере
-
становки α для всех α ∈S
5
.
Рассмотрим многочлен
√
D =
Q
i< j
(x
i
−x
j
). Выполняется тождество
α
√
D = ε(α)
√
D
для α ∈S
5
.

316 Глава IV. Алгебраические уравнения
Заметим, что
α
f
√
D
=
αf
α
√
D
=
ε(α) f
ε(α)
√
D
=
f
√
D
.
Поэтому
¯
f =
f
√
D
∈C(σ
0
, σ
1
, σ
2
, σ
3
, σ
4
),
значит, K
0
(f) = K
0
¯
f
√
D
= K
0
√
D
.
Далее понадобится еще
Лемма 31. Поле
K
1
= K
0
√
D
⊂C(x
1
, x
2
, ..., x
5
)
совпадает с множеством всех рациональных функций, не изменя-
ющихся при четных перестановках переменных.
Д о к а з а т е л ь с т в о. Проверим, что рациональная функция f
не изменяется при четных перестановках переменных тогда и только
тогда, когда она представляется в виде суммы симметрической функции
f
1
и антисимметрической функции f
2
(т. е. такой, что αf = ε(α) f для
α ∈S
5
). В одну сторону это очевидно.
Докажем обратное утверждение. В самом деле,
f =
1
2
(f + (12) f) +
1
2
(f − (12) f), f
1
=
1
2
(f + (12) f), f
2
=
1
2
(f − (12) f).
Проверим симметричность f
1
, т. е. равенство αf
1
= f
1
. Если α
––
чет
-
ная, то αf
1
=
1
2
(αf + α(12) f) =
1
2
(f + (12)(12)α(12) f), но перестановка
(12)α(12)
––
четная, значит, (12)α(12) f = f, откуда α f
1
=
1
2
(f + (12) f) = f
1
.
Аналогично проверяем равенство αf
2
= f
2
:
αf
2
=
1
2
(αf −α(12) f) =
1
2
f −
1
2
((12) (12)α(12) f) =
1
2
(f − (12) f) = f
2
.
Если перестановка α
––
нечетная, то
αf
1
=
1
2
(αf + α(12) f) =
1
2
((12) (12)αf + α(12) f) =
1
2
((12) f + f) = f
1
,
т. к. перестановки (12)α и α(12)
––
четные. Кроме того,
αf
2
=
1
2
(αf −α(12) f) =
1
2
((12) (12)αf −α(12) f) = −f
2
.
Поэтому, если f
––
рациональная функция, не меняющаяся при четных
перестановках, то f = f
1
+ f
2
, где f
1
––
симметрическая, а f
2
––
антисим
-
метрическая функция.
§ 4.20. Теорема Абеля
––
Руффини 317
Если f
2
––
антисимметрическая функция, то f
2
=
f
2
√
D
√
D =
¯
f
2
√
D,
где
¯
f
2
––
симметрическая функция. Поэтому f = f
1
+
¯
f
2
√
D, где f
1
и
¯
f
2
––
симметрические функции, и f ∈ K
0
√
D
= K
1
.
Обратно, если f ∈K
0
√
D
= K
1
, то f = f
1
+ f
2
√
D, где f
1
и f
2
––
сим
-
метрические функции, значит, f не меняется при четных переста
-
новках.
Нужны будут еще две леммы о перестановках.
Лемма 32. Любая четная перестановка разлагается в произве-
дение тройных циклов.
Д о к а з а т е л ь с т в о. Разложим четную перестановку в произве
-
дения четного числа транспозиций, разобьем это произведение на пары,
а пары заменим на тройные циклы согласно тождеству
(i, j) (i
′
, j
′
) = (i ji
′
)(ji
′
j
′
).
Лемма 33. Если перестановка (i
1
, ..., i
5
) разложима, то справед-
ливо тождество
(i
1
, i
2
, i
3
) = (i
4
, i
3
, i
1
)(i
1
, i
5
)(i
2
, i
4
)(i
3
, i
4
)(i
1
, i
5
)(i
1
, i
3
, i
4
).
Д о к а з а т е л ь с т в о. Для доказательства достаточно проверить,
что под действием произведения перестановок элементы передвигаются
следующим образом:
i
1
→i
3
→i
4
→i
2
, i
2
→i
4
→i
3
,
i
3
→i
4
→i
3
→i
1
, i
4
→i
1
→i
5
→i
1
→i
4
.
Закончим доказательство теоремы. Пусть K
2
= K
1
r
√
a
, a ∈ K
1
,
r > 2, и
r
√
a = f(x
1
, x
2
, x
3
, x
4
, x
5
) ∈C(x
1
, x
2
, x
3
, x
4
, x
5
).
Тогда для всякой перестановки α ∈S
5
имеет место равенство αf = ε
α
f,
где ε
α
∈
r
√
a.
Заметим, что если {ij} ∩{i
′
j
′
} = ∅, то ε
(i j) (i
′
j
′
)
= ±1, так как
[(ij) (i
′
j
′
)]
2
––
тождественная перестановка.
Применяя лемму 33 и учитывая, что
ε
(i
4
,i
3
,i
1
)
·ε
(i
1
,i
3
,i
4
)
= ε
(i
4
,i
3
,i
1
)
·ε
(i
4
,i
3
,i
1
)
−1
+ 1,
имеем
ε
(i
1
,i
2
,i
3
)
= ε
(i
4
,i
3
,i
1
)
ε
(i
1
,i
3
,i
4
)
ε
(i
1
,i
5
) (i
2
,i
4
)
ε
(i
3
,i
4
) (i
1
,i
5
)
,
откуда ε
(i
1
i
2
i
3
)
= ±1.
Однако (i
1
i
2
i
3
)
3
––
тождественная перестановка, значит, ε
3
(i
1
i
2
i
3
)
= ±1.
Поэтому ε
(i
1
,i
2
,i
3
)
= 1.

318 Глава IV. Алгебраические уравнения
Из леммы 32 теперь следует, что ε
α
= 1 для всякой четной переста
-
новки α.
Из леммы 31 тогда следует, что K
2
= K
1
r
√
a
= K
1
(f), f ∈K
1
, откуда
K
2
= K
1
. Повторяя эти рассуждения, получаем, что
K
1
= K
2
= K
3
= ... = K
n
.
Однако, согласно лемме 31, поле K
1
есть множество рациональных
функций от (x
1
, x
2
, x
3
, x
4
, x
5
), не меняющихся при четных перестановках
переменных, следовательно, оно не совпадает с полем всех рациональных
функций C(x
1
, x
2
, x
3
, x
4
, x
5
). Значит, искомая цепочка расширений невоз
-
можна.
Задачи и упражнения к § 4.20
1. Решите уравнение x
5
−5ax
3
+ 5a
2
x + a
5
+ 1 = 0.
2. С помощью замены переменных x = u + v решите подобно куби
-
ческому уравнению уравнение x
5
−5ax
3
+ 5a
2
x −2b = 0.
Приложение. Образцы контрольных работ
разных лет, экзаменационных вопросов
и задач
Контрольная работа 1
1. Разложите на множители (с действительными коэффициентами) (i) x
4
+9; (ii) x
4
+25.
2. Докажите, что числа (i)
√
2 +
√
3; (ii)
√
3 +
√
5
––
иррациональны.
3. Решите уравнения:
(i) x
4
−4x
3
−2x
2
+ 12x + 8 = 0; (ii) x
4
−10x
3
+ 4x
2
+ 8 = 0.
4. Докажите неравенства:
(i)
1
2
3
4
5
6
.. .
2n −1
2n
<
1
√
2n
; (ii)
1
2
3
4
5
6
. . .
2n −1
2n
>
1
2
√
n
.
Контрольная работа 2
1. Найдите суммы: (i)
n
X
k=1
k(3k + 1); (ii)
n
X
k=1
(k
2
+ 2k −1).
2. С помощью алгоритма Евклида найдите НОД чисел a и b и представьте его в виде
au + bv, где u и v
––
целые: (i) a = 24, b = 30; (ii) a = 36, b = 20.
3. Найдите число и сумму всех натуральных делителей у чисел (i) 2772; (ii) 5940.
4. Вычислите значение функции Эйлера от чисел (i) 65; (i) 72.
5. В разложениях (i) (x + 1
/
x)
12
; (ii) (x
/
3 −3
/
x)
12
найдите коэффициент при (i) x
8
;
(ii) x
4
.
6. Найдите суммы: (i) C
0
n
+ C
2
n
+ . . . + C
2k
n
+ . . .; (ii) 1 −C
1
n
+ C
2
n
−C
3
n
+ . . .
Контрольная работа 3
1. Найдите порядок подстановки π и определите ее знак:
(i) π =
“
12345
24513
”
; (ii) π =
“
123456
345612
”
.
2. В произвольной группе G определена новая операция
[f, g] = f
−1
g
−1
fg.
Докажите тождества: (i) [f, g]
−1
= [g, f], (ii) fg [g, f] = fg.
3. Решите уравнения:
(i) x
4
−5x
2
−2x + 3 = 0; (ii) x
4
−5x
2
+ 2x + 3 = 0.
4. Докажите для любых неотрицательных a и b неравенства:
(i) a
3
+ b
3
> ab(a + b); (ii) (a
3
+ b
3
) (a + b) > (a
2
+ b
2
)
2
.
5. Докажите, что уравнение x
3
−3x + 1 = 0 имеет три корня, и найдите сумму их
(i) квадратов; (ii) кубов, а также уравнение, одним из корней которого является (i) сум
-
ма; (ii) произведение двух корней исходного уравнения.

320 Приложение
6. Вычислите
(i)
n
X
k=1
kC
k
n
; (ii)
n
X
k=1
(n −k)C
k
n
.
7. Найдите группу самосовмещений многочлена при перестановках переменных
(xz + yt)
2
+ (xy − zt)
2
и разложите его на множители.
8. Первенство интерната по футболу проводилось настолько нерегулярно, что в конце
семестра выяснилось, что все команды сыграли разное число матчей. Докажите, что какие
-
то команды успели сыграть между собой более одного раза.
Вопросы к экзамену в 10
-
х классах (1999 год)
1. Индукция и примеры ее применения. Формулы суммирования арифметической и гео
-
метрической прогрессий.
2. Числа Фибоначчи. Формула Бине.
3. Рекуррентные последовательности второго порядка.
4. Простые числа. Бесконечность множества простых чисел. Наибольший общий де
-
литель и наименьшее общее кратное.
5. Алгоритм Евклида. Линейное представление наибольшего общего делителя. Леммы
о делимости.
6. Основная теорема арифметики.
7. Перестановки и размещения.
8. Перестановки с повторениями.
9. Биномиальная теорема. Треугольник Паскаля. Тождество Паскаля.
10. Биномиальная и полиномиальная теоремы.
11. Сочетания с повторениями.
12. Определение комплексных чисел. Операции над ними. Геометрическая интерпре
-
тация комплексных чисел.
13. Многочлены и операции над ними. Деление с остатком.
14. Схема Горнера. Теорема Безу. Теорема о числе корней у уравнений произвольной
степени.
15. Производные и кратные корни.
16. Теорема Виета для уравнений произвольной степени.
17. Алгоритм Евклида для многочленов. Линейное представление наибольшего общего
делителя. Леммы о делимости многочленов. Понятие неприводимого многочлена.
18. Однозначность разложения на множители многочленов над полем рациональных
чисел.
19. Операция сопряжения и свойства комплексных корней многочленов с действитель
-
ными коэффициентами.
20. Разложение на множители многочленов над полями действительных и комплексных
чисел.
21. Умножение и деление комплексных чисел в тригонометрической форме. Теоремы
сложения для синуса и косинуса.
22. Формулы Муавра и Эйлера. Формулы для синусов, косинусов и тангенсов крат
-
ных дуг.
23. Извлечение корней n
-
й степени из комплексных чисел. Геометрическая интерпре
-
тация.
24. Алгебраический метод извлечения квадратных корней из комплексных чисел. Ре
-
шение квадратных уравнений в поле комплексных чисел.
25. Группа корней n
-
й степени из единицы. Первообразные корни. Функция Эйлера
и ее мультипликативное свойство. Формула Эйлера.
