Гаркушенко В.И. Лекции по ТАУ
Подождите немного. Документ загружается.

131
числе, входными сигналами, которое с течением времени для устойчивой сис-
темы затухает, т.е. стремится к нулю. Установившееся движение зависит толь-
ко от вида входного воздействия. Оценка качества процессов или движения
САР проводится для переходного и установившегося движения.
Показатели качества регулирования делятся на прямые и косвенные пока-
затели качества.
2. Прямые показатели качества.
В инженерной практике наибольшее распространение получили показа-
тели качества для переходной характеристики выхода системы – реакции выхо-
да системы
( )
y t
на ступенчатое входное воздействие
0
( ) 1( )
g t g t
,
0
g const
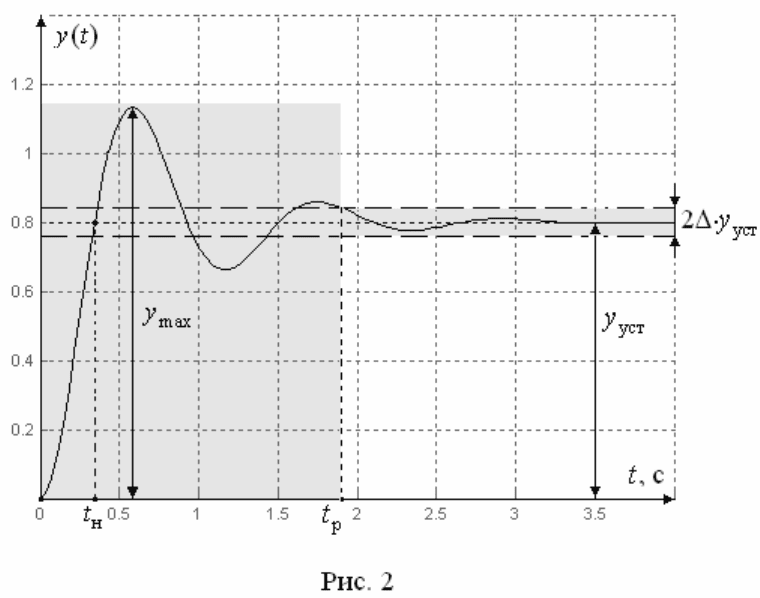
при отсутствии возмущения и нулевых начальных условиях (рис. 2).
Здесь определяются следующие прямые показатели качества:
для установившегося движения
1установившаяся ошибка
уст 0 ос уст
g y
;
для переходного движения
2время регулирования
p
t
– минимальное время, по истечении которого
132
выходная координата
( )
y t
входит в трубку величиной
уст
2
y
и не покидает
ее, т.е. выполняется условие
уст уст
| ( ) |
y t y y
для
p
t t
(обычно
0,05
);
3перерегулирование
, которое определятся по формуле
max уст
уст
100
y y
y
%. (1)
4) время нарастания
н
t
– минимальное время, при котором
н уст
( )
y t y
.
5) число колебаний
( )
y t
на интервале времени
p
0
t t
.
Наилучшим считается процесс с наименьшими значениями указанных по-
казателей качества или принадлежащий заданной закрашенной области рис.2.
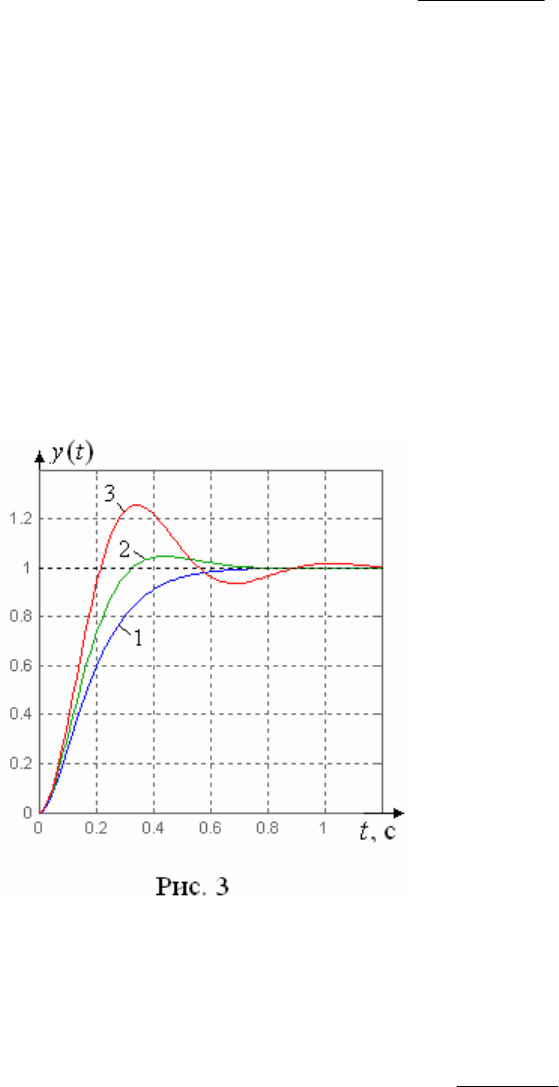
Переходные движения, вызванные ступенчатыми входными воздейст-
виями, принято делить на три группы (рис. 3): 1-монотонные, 2-апериодические
и 3-колебательные.
У монотонных процессов первая производная
( )
y t
не меняет знак, у апериодических знак
производной меняется не более одного раза, а
у колебательных производная
( )
y t
меняет
знак периодически.
Установившаяся ошибка устойчивой
системы может быть найдена по теореме о
конечном значении оригинала
уст
0
lim ( ) lim ( )
t p
t pE p
, (2)
если известно, что существует предел
уст
lim ( )
t
t const
. Здесь изображение
ошибки по Лапласу
( )
E p
для системы рис. 1 определяется по формуле
1
( ) ( )
1 ( )
E p G p
W p
,
где
1 2 ос
( ) ( ) ( ) ( )
W p W p W p W p
– передаточная функция разомкнутой системы.
а) Для входного сигнала
0
( ) 1( )
g t g t
, соответственно
0
( ) /
G p g p
. Тогда

133
получим изображение ошибки
0
1
( )
1 ( )
g
E p
W p p
.
Полагая
(0) / 0
m n
W b a k
, где
k
– коэффициент усиления разомкну-
той системы, найдем
0
уст ст
0
lim ( )
1
p
g
p p
k
. (3)
Значение ошибки
ст
называется статической ошибкой. Система, у которой
статическая ошибка не равна нулю, называется статической по отношению к
заданному входному воздействию. Система, у которой статистическая ошибка
равна нулю, называются астатической.
Таким образом, установившаяся ошибка согласно выражению (3) зависит
от коэффициента передачи разомкнутой системы
k
, т.е. чем больше его значе-
ние, тем меньше установившаяся ошибка.
Астатизм системы обусловлен наличием в разомкнутой системе интегри-
рующих звеньев, т.е. ее передаточная функция может быть представлена в ви-
де:
раз
( )
( )
( )
v
v
m p
W p
p d p
,
где
,...
2
,
1
v
– порядок астатизма, полином
( )
v
d p
не имеет нулевых корней.
Действительно, в этом случае при постоянном входном воздействии по-
лучим
0
уст
0
( )
lim 0
( ) ( )
v
v
v
p
v
p d p g
p
p
p d p m p
.
б) Если входное воздействие является линейно нарастающей функцией
времени
1
( )
g t g t
, соответственно
2
1
( ) /
G p g p
, и степень астатизма
1
v
астатизм первого порядка), то
1 1 1
уст ск
2
0
1
( )
lim
( ) ( )
p
pd p g g
p
pd p m p k
p
, (5)
134
где
1
(0)/ (0) 0
k m d
,
ск
– называется скоростной ошибкой.
Для системы с астатизмом второго порядка (
2
v
) в этом случае устано-
вившаяся ошибка, очевидно, равна нулю.
При наличии возмущения
( )
f t
установившаяся ошибка определяется
аналогично и равна сумме установившихся ошибок от входа
( )
g t
и возмущения
( )
f t
, найденных отдельно.
2. Косвенные показатели качества.
При расчетах САР прямые показатели качества оцениваются с помощью
косвенных показателей, которые делятся на алгебраические, частотные и инте-
гральные показатели.
1. Алгебраические показатели качества позволяют судить о качестве
переходного процесса по коэффициентам или корням характеристического
уравнения.
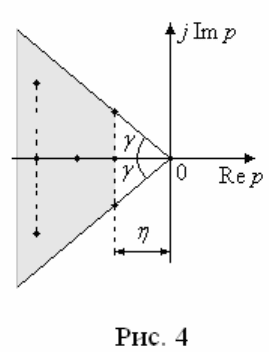
Рассмотрим корневые показатели качества, связанные с распределением
левых корней на комплексной плоскости (рис. 4). Здесь используют степень
устойчивости и колебательности.
а) Степенью устойчивости
называется
расстояние от мнимой оси до ближайшего левого корня.
Степень устойчивости характеризует быстродействие
системы.
Это связано с тем, что быстрота затухания переходного
процесса в значительной мере определяется
вещественной частью корня, наиболее близко располо-
женного к мнимой оси. При этом справедлива оценка
для времени регулирования
p
3 5/
t
.
Если ближайшим к мнимой оси является вещественный корень, то ему
соответствует апериодическая составляющая переходного процесса
1
t
e c
(апе-
риодическая степень устойчивости).
Пример 1. Рассмотрим систему первого порядка
135
( ) ( ) 1( )
y t ay t k t
,
для которой найдем решение
( )
y t
. Изображение выхода в преобразованиях Ла-
пласа при нулевом начальном условии
(0) 0
y
имеет вид
1 1
( )
( )
k k
Y p
p a p a p p a
,
которому соответствует оригинал
( ) 1( )
at
k
y t t e
a
.
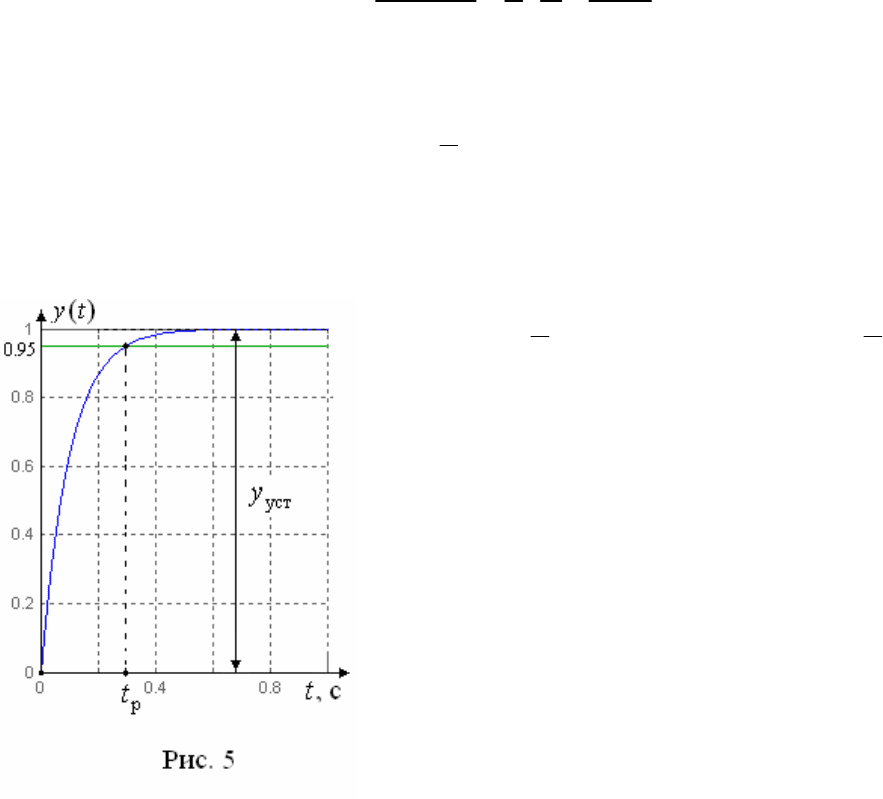
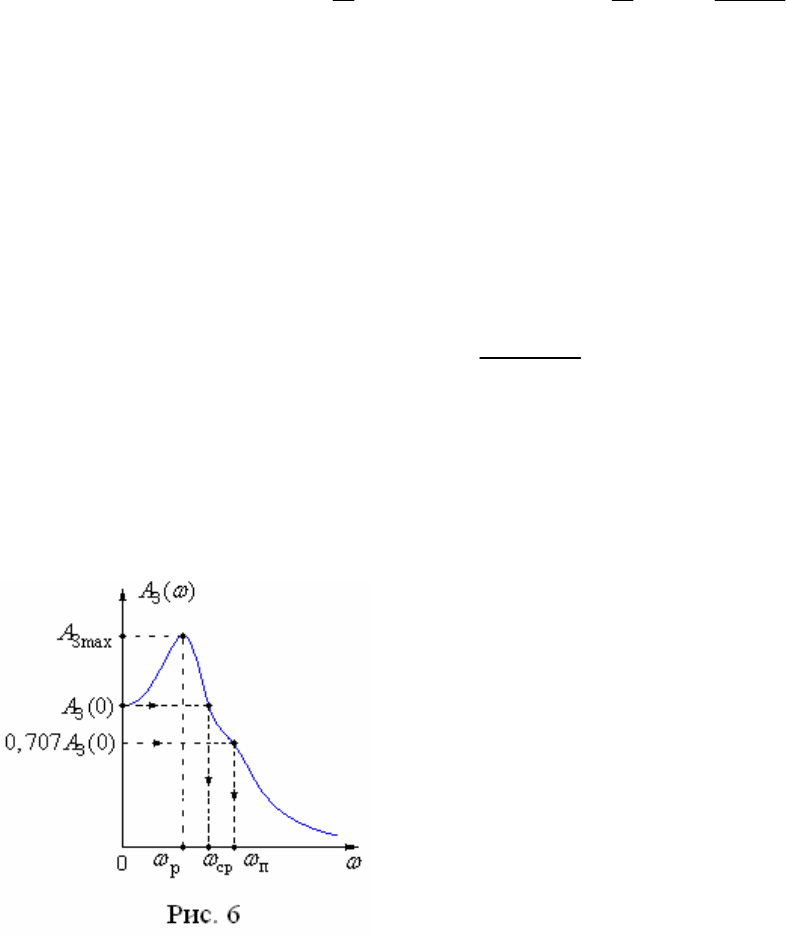
Реакция выхода системы
( )
y t
при
10
a k
представлена на рис. 5, из
которого следует, что время регулирования определяется из уравнения
p
p уст
1 1
( ) 1 0,95 0,95
at
y t e y
a a
.
Отсюда найдем
p
0,05
at
e
или
p
ln0,05/ 3/
t a a
. Поскольку
a
, то для
системы первого порядка справедлива оценка
p
3/
t
. Здесь на рис. 5 время регулирования
p
0,3
t
с.
Если же ближайшей к мнимой оси
окажется пара комплексно-сопряженных корней
1,2
p j
, то доминирующая составляющая
переходного процесса
( sin cos )
t
e A t B t
является колебательной (колеба-
тельная степень устойчивости).
Для определения степени устойчивости по характеристическому уравне-
нию системы
( ) 0
d p
проведем замену
p p
. Тогда получим характери-
стическое уравнение
( , ) 0
d p
, коэффициенты которого зависят от неизвест-
ного параметра
. С помощью критерия Гурвица можно найти область устой-
чивости по параметру
0
, верхняя граница которого определяет значение
степени устойчивости системы, поскольку при корнях уравнения
( , ) 0
d p
,
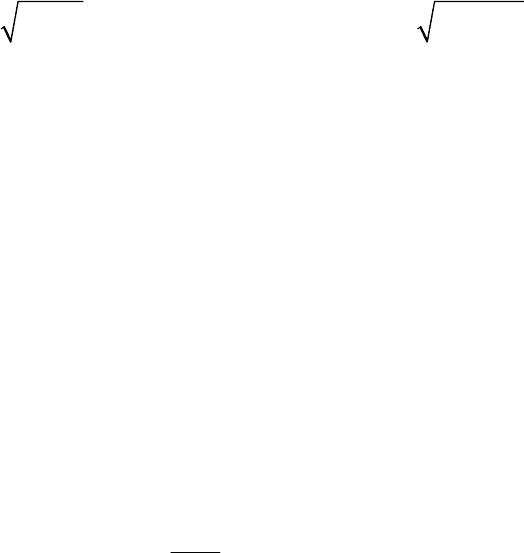
136
расположенных на мнимой оси, корни уравнения
( ) 0
d p
имеют степень ус-
тойчивости
.
в) При наличии комплексно-сопряженных корней используется степень
колебательности, которая характеризует быстроту затухания колебаний за ка-
ждый период и определяется величиной
tg
, где
– наименьший угол сектора,
которому принадлежат левые корни на комплексной плоскости (рис. 4).
Действительно, для пары комплексно-сопряженных корней
1,2
p j
,
0
,
0
, которым соответствует равенство
/
tg
, составляющую ре-
шения можно представить в виде
( sin cos )
t
e A t B t
с периодом колебаний
к
2 /
T
. Тогда через один период амплитуда
t
e
уменьшится до величины
( 2 / ) 2 /
t t
e e e
, т.е. чем больше величина
/
, тем слабее будет за-
тухание колебаний для данной составляющей переходного процесса.
Отметим, что комплексно-сопряженным корням
1,2
p j
соответ-
ствует полином
2 2
2 1
T p T p
при
0 1
, для которого справедливы равен-
ства
/
T
,
2
1 /
T
. Тогда получим
2
/ 1/ 1
, т.е. степень ко-
лебательности зависит от коэффициента демпфирования
.
2. Частотные показатели качества позволяют судить о качестве пере-
ходного процесса по частотным характеристикам замкнутой и разомкнутой
системы. Основанием для этого служит связь весовой характеристики системы
с ее частотной характеристикой, построенной по передаточной функции или
экспериментально.
Действительно, если известна передаточная функция системы (замкнутой
или разомкнутой)
( )
W p
, то согласно обратному преобразованию Лапласа весо-
вую функцию можно найти по формуле
1
( ) ( )
2
j
pt
j
w t W p e dp
j
, (6)
где путь интегрирования в комплексной плоскости
p
выбирается правее полю-

137
сов изображения
( )
W p
, при которых оно обращается в бесконечность. Для ус-
тойчивых систем полюса передаточной функции
( )
W p
лежат в левой полу-
плоскости, поэтому в формуле (6) можно положить
0
и
p j
. Учитывая,
что при замене переменной
p j
изменяются пределы интегрирования
j
j
p j
в формуле (6), получим формулу обратного преобразования Фу-
рье:
1
( ) ( )
2
j t
w t W j e d
,
(7)
где АФЧХ
( )
W j
называется изображение Фурье весовой функции
( )
w t
для
значений
0
t
. При этом
( ) 0
w t
, т.е. справедливо выражение
1
0 ( )
2
j t
W j e d
. (8)
Суммируя выражения (7) и (8) получим
0
0
0
0
0
1 1
( ) ( ) ( )cos
2
1
( )cos ( )cos
1
( )cos ( )cos
1
( ) ( ) cos .
j t j t
w t W j e e d W j td
W j td W j td
W j td W j td
W j W j td
.
С учетом равенства
( ) ( ) ( )
W j P jQ
найдем
0
2
( ) ( )cos
w t P td
.
(9)
Для определения переходной функции проинтегрируем выражение (9) по
времени:
138
0 0 0 0
2 2 sin
( ) ( ) ( ) cos ( )
t t
t
h t w d P tdtd P d
. (10)
Тем самым, зная вещественную частотную характеристику
( )
P
, можно
построить переходную характеристику
( )
h t
одним из способов приближенного
вычисления интеграла (10), приведенного в [1]. При этом характер переходного
процесса зависит от вида частотной характеристики
( )
P
.
а) Для замкнутой системы с передаточной функцией
З
( )
( )
1 ( )
W p
W p
W p
где
( )
W p
– передаточная функция разомкнутой системы строится амплитудно-
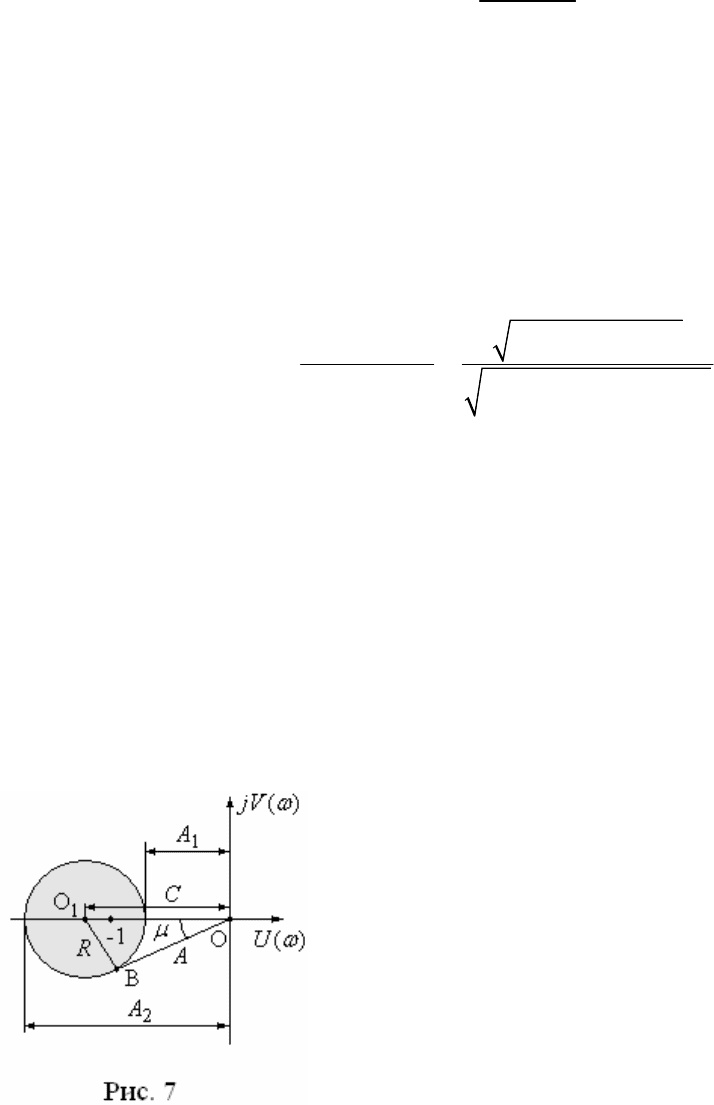
частотная характеристика
З З
( ) | ( )|
A W j
(рис. 6). Здесь
p
– резонансная
частота, при которой
З
( )
A
достигает максимального значения
max
З
A ;
п
–
частота, при которой
З п З
( ) 0,707 (0)
A A
, оп-
ределяет полосу пропускания системы
п
(0, )
.
Полоса пропускания не должна быть слишком
широкой, иначе система будет воспроизводить
высокочастотные помехи. Частота среза
ср
,
при которой
З ср
( ) 1
A
, косвенно характеризу-
ет время регулирования
p ср
(1 2) 2 /
t
, т.е.
чем больше частота среза
ср
, тем меньше длительность переходного процесса.
Физически это связано с тем, что чем более высокие частоты пропускает систе-
ма, тем менее она инерционна в своих реакциях на входные воздействия.
Другой оценкой качества переходного процесса является показатель ко-
лебательности
max З
/ (0)
З
M A A
, величина которого характеризует склонность
системы к колебаниям. Чем выше значение
M
, тем менее качественна система
при прочих равных условиях.
При проектировании линейных САР принято задаваться значениями
1,1 1,7
M
. При этом значениям
1,1 1,3
M
соответствует очень хорошее
139
демпфирование, значениям
1,3 1,5
M
– хорошее демпфирование, значениям
1,5 1,7
M
– удовлетворительное демпфирование переходного процесса.
Обеспечение малых значений показатель колебательности
1 1,1
M
тре-
бует применения более сложных и дорогостоящих корректирующих средств и
ведет к неоправданному усложнению системы.
Для астатической САР
З
(0) 1
A
, для статической САР
З
(0)
(0)
1 (0)
W
A
W
и при
(0) 1
W
значение
З
(0) 1
A
. Поэтому в дальнейшем будем полагать
max
З
M A
. Физически это означает, что в установившемся режиме выход сис-
темы равен входному постоянному сигналу.
По известной АФЧХ разомкнутой системы
( ) ( ) ( )
W j U jV
можно
найти значение
M
с помощью выражения
2 2
2
2
( ) ( )
| ( )|
|1 ( )|
1 ( ) ( )
U V
W j
M
W j
U V
.
Отсюда получим
2
2 2 2 2
( ) ( ) 1 ( ) ( )
U V U V M
или
2
2 2
( ) ( )
U C V R
, (6)
где
2 2
/( 1)
C M M
,
2
/( 1)
R M M
.
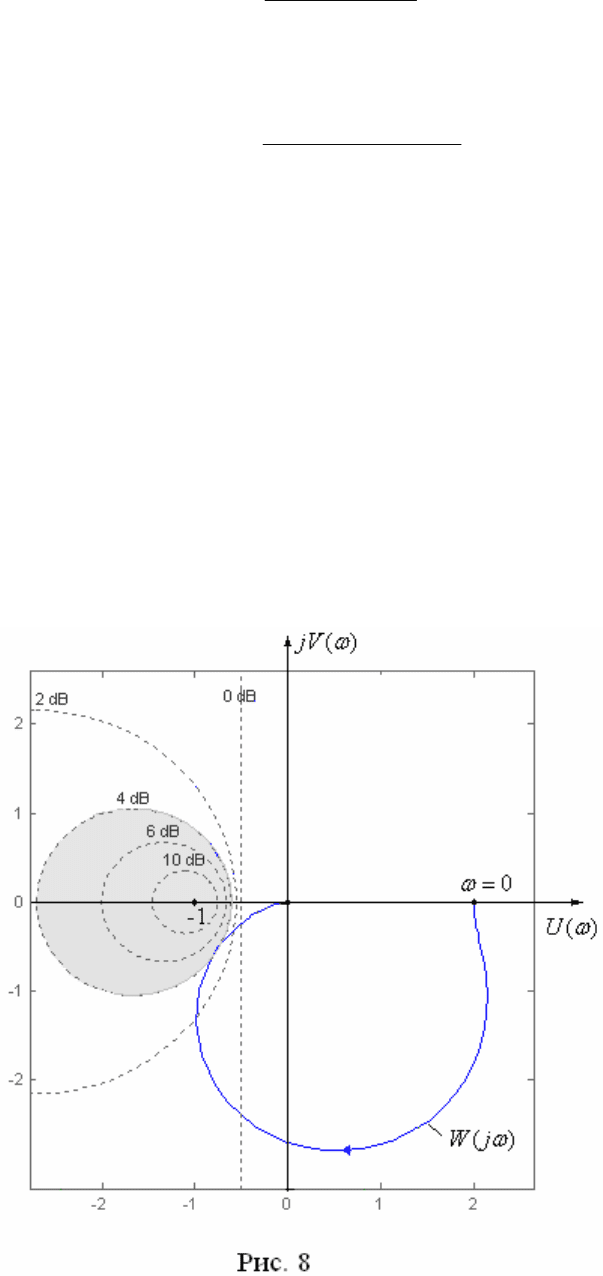
Задавая различные значения
M
по формуле (6) можно построить семей-
ство окружностей со смещенным центром
C
и ра-
диусом
R
на комплексной плоскости (рис. 7). Здесь
угол
является запасом устойчивости по фазе для
той системы, у которой АФЧХ
( )
W j
касается ок-
ружности
const
M
в точке
B
. Величину
можно
определить из треугольника
1
OBO
с учетом теоремы
косинусов
140
2 2 2
2 cos
R A C AC
,
откуда
2 2 2
cos
2
A C R
AC
.
С учетом выражений для
C
,
R
получим
2 2 2
2
( 1)
arccos
2
M A M
AM
. (7)
Из рис. 7 следует, что зависимость (7) существует только для модулей
A
,
лежащих в пределах
1 2
A A A
, где
1
/( 1)
A M M
,
2
/( 1)
A M M
,
1
M
.
Вне этих пределов запас по фазе может быть любым, так как в этом случае ко-
нец вектора не может попасть в запретную область.
После построения АФЧХ разомкнутой системы
( )
W j
показатель коле-
бательности
M
определяется по точке касания к одной из окружностей.
На рис. 8 представлена АФЧХ и окружности (6), на которых для удобства
вместо значений
M
указаны значения
20lg
M
. Здесь значению
20lg 4
M
дБ
