Гаркушенко В.И. Лекции по ТАУ
Подождите немного. Документ загружается.

121
Если АФЧХ разомкнутой системы не имеет переходов вещественной по-
луоси
( , 1)
, то сумма переходов равна нулю.
2. Логарифмический аналог критерия Найквиста.
Установим связь переходов для АФЧХ с переходами для ЛАХ и ЛФХ.
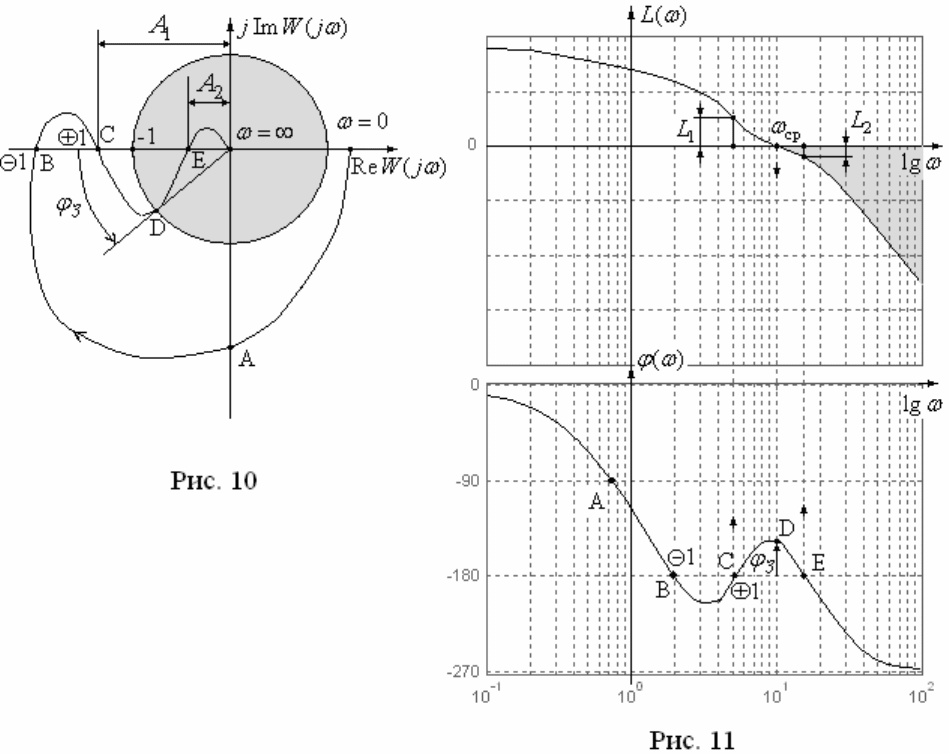
Для этого рассмотрим рис. 10 и рис. 11, на которых отмечены характерные
точки. На рис. 10 и рис. 11 отрицательному переходу соответствует убывание, а
положительному возрастание значения
( )
.
Если АФЧХ разомкнутой системы, представленной на рис. 10, зеркально
отобразить относительно вещественной оси, то ЛФХ на рис. 11 также зеркально
отобразиться относительно оси частот, а ЛАХ при этом останется прежней. Для
такой разомкнутой системы условие устойчивости по критерию Найквиста не
изменится. В этом случае ЛФХ будет пересекать ось
.
Таким образом, переходам АФЧХ вещественной полуоси
( , 1)
на
рис.10 соответствует область положительных значений
( )
L
, для которых

122
| ( )| 1
W j
, и значение
( ) ; 3 ; 5 ;
. Область, в которой
| ( )| 1
W j
или
( ) 20lg| ( )| 0
L W j
(на рисунках закрашена) не влияет на устойчивость
замкнутой системы. Значение частоты
ср
, при которой
ср
| ( )| 1
W j
или
ср
( ) 1
L
называется частотой среза. В общем случае может существовать не-
сколько частот среза, т.е. несколько участков положительных значений ЛАХ.
С помощью переходов критерий Найквиста можно сформулировать так:
Для устойчивости замкнутой системы с единичной отрицательной об-
ратной связью необходимо и достаточно, чтобы в области частот, где
( ) 0
L
, сумма переходов с учетом знаков ЛФХ разомкнутой системы через
линии
( ) ; 3 ; 5 ;
равнялась
/2
m
, где
m
– число правых корней
характеристического уравнения разомкнутой системы.
3. Запасы устойчивости.
Запасы устойчивости – это величины, которые количественно характери-
зуют удаление устойчивой системы от границы ее устойчивости. На комплекс-
ной плоскости для левых корней характеристического уравнения запасом ус-
тойчивости можно считать наименьшее расстояние корня до мнимой оси. Запа-
сом устойчивости замкнутой системы можно считать удаление АФЧХ разомк-
нутой системы от точки
( 1, 0)
j
.
Действительно, если АФЧХ разомкнутой системы
( )
W j
при
0
0
проходит через точку
( 1, 0)
j
, то замкнутая система имеет пару чисто мнимых
корней. Это следует из условия
0
( ) 1
W j
, которому соответствует уравне-
ние
0
0
0
( )
1 ( ) 0
( )
D j
W j
d j
,
где характеристическое уравнение замкнутой системы
0
( ) 0
D j
должно име-
ть пару чисто мнимых корней
1,2 0
p j
.
Если АФЧХ разомкнутой системы
( )
W j
при
0
начинается из точки
( 1, 0)
j
, то замкнутая система имеет нулевой корень.
Таким образом, при выполнении устойчивости замкнутой системы АФЧХ

123
разомкнутой системы не должна проходить вблизи точки
( 1, 0)
j
. Удаление от
этой точки характеризуется запасами по амплитуде
1
A
,
2
A
(рис. 10) или
1 1
20lg
L A
,
2 2
|20lg |
L A
(рис. 11), запасами по фазе
З
, равные ближайшим
углам между вещественной полуосью
( , 0]
и лучам, проходящим через нача-
ло координат и соответствующую точку
ср
( )
W j
.
4. Устойчивость систем с запаздыванием.
Система с запаздыванием имеет передаточную функцию разомкнутой
системы, содержащую звено чистого запаздывания
p
e
:
0
( ) ( )
p
W p W p e
, (3)
где
0
( ) ( )/ ( )
W p m p d p
– физически реализуемая передаточная функция. По-
скольку характеристическое уравнение замкнутой системы
( ) ( ) ( ) 0
p
D p d p m p e
(4)
не является алгебраическим полиномом, то критерий Гурвица здесь не приме-
ним. Кроме того, функция
2 2
1 /2! ( 1) / !
p N N
e p p N
являет-
ся бесконечным рядом степени
p
, т.е. уравнение (4) имеет бесчисленное мно-
жество корней. Поэтому критерий Михайлова также не применим. Однако от-
ветить на вопрос об устойчивости корней характеристического уравнения (4)
можно с помощью критерия Найквиста. Для этого вместо передаточной функ-
ции (3) будем использовать приближенную передаточную функцию
0
( )
( ) ( )
( )( 1)
p p
N
m p
W p W p e e
d p p
, (5)
где
– сколь угодно малое,
N
сколь угодно большое целое число. Очевидно,
что при
0
передаточная функция
( ) ( )
W p W p
. Также отметим, что при
0
согласно критерию Найквиста устойчивость замкнутой системы не зави-
сит от сколь угодно малой постоянной времени
.
Передаточной функции (5) соответствует функция
( )( 1) ( )
( ) 1 ( )
( )( 1)
N p
N
d p p m p e
F p W p
d p p
,
124
у которой при
N
порядок полиномов числителя и знаменателя можно счи-
тать одинаковыми. Тогда согласно критерию Найквиста для устойчивости
замкнутой системы необходимо и достаточно, чтобы приращение аргумента
функции
( )
F j
при изменении
0
было равно
2 /2
m
раз, где
m
–
число правых корней характеристического уравнения
( )( 1) 0
N
d p p
или
уравнения
( ) 0
d p
. При
0
функция
( ) ( )
F j F j
и условие устойчиво-
сти сохраняется, т.е. совпадает с условием устойчивости системы без запазды-
вания. Поэтому для исследования устойчивости замкнутой системы с переда-
точной функцией разомкнутой системы (3) необходимо построить ее АФЧХ и
применить критерий Найквиста.
Выражение АФЧХ имеет вид:
0
( ( ) )
0 0
( ) ( ) | ( )|
j
j
W j W j e W j e
. (6)
Из формулы (6) следует, что при наличии запаздывания вектор
0
( )
W j
поворачивается на угол
, не меняя своей длины, что приводит к повороту
АФЧХ по часовой стрелке. Если без учета запаздывания замкнутая система ус-
тойчива и на частоте среза
ср
имеет запас устойчивости по фазе
З
, то систе-
ма с запаздыванием выходит на границу колебательной устойчивости при неко-
тором критическом значении
кр
, если
ср кр
З
, т.е. при
кр ср
/
З
.
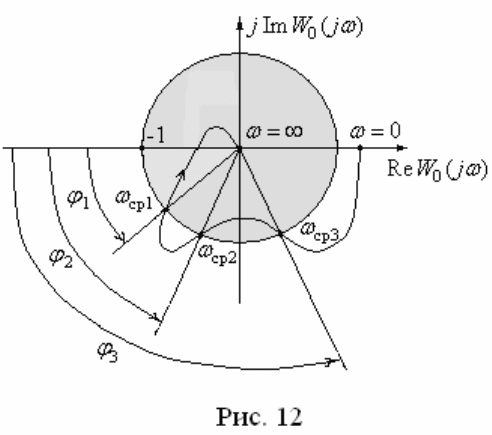
Для АФЧХ
0
( )
W j
, представленной на рис. 12, найдем критические
125
значения времени запаздывания по формуле
кр ср
/
i i i
,
1,3
i
. Тогда со-
гласно критерию Найквиста для
0
m
замкнутая система будет устойчивой при
кр1
0
,
кр2 кр3
и неустойчивой при
кр1 кр2
.
5. Интервальный критерий Найквиста.
В качестве обобщения критерия Найквиста рассмотрим систему, у кото-
рой физически реализуемая передаточная функция разомкнутой системы имеет
вид
1 2
( ) ( ) ( )
W p W p W p
, (7)
где
1
( )
W p
– известная физически реализуемая передаточная функция,
2
( )
W p
–
передаточная функция, зависящая от некоторых параметров, за счет выбора ко-
торых она может принимать значение
2
( ) 1
W p
. Передаточную функцию
2
( )
W p
также можно считать обратной связью, для охватываемой передаточной
функции
1
( )
W p
. Найдем условия устойчивости замкнутой системы.
При выполнении условия
1 2
( ) ( ) 1
W j W j
или
1 2
( ) 1/ ( )
W j W j
замкнутая система имеет корни характеристического уравнения
p j
, распо-
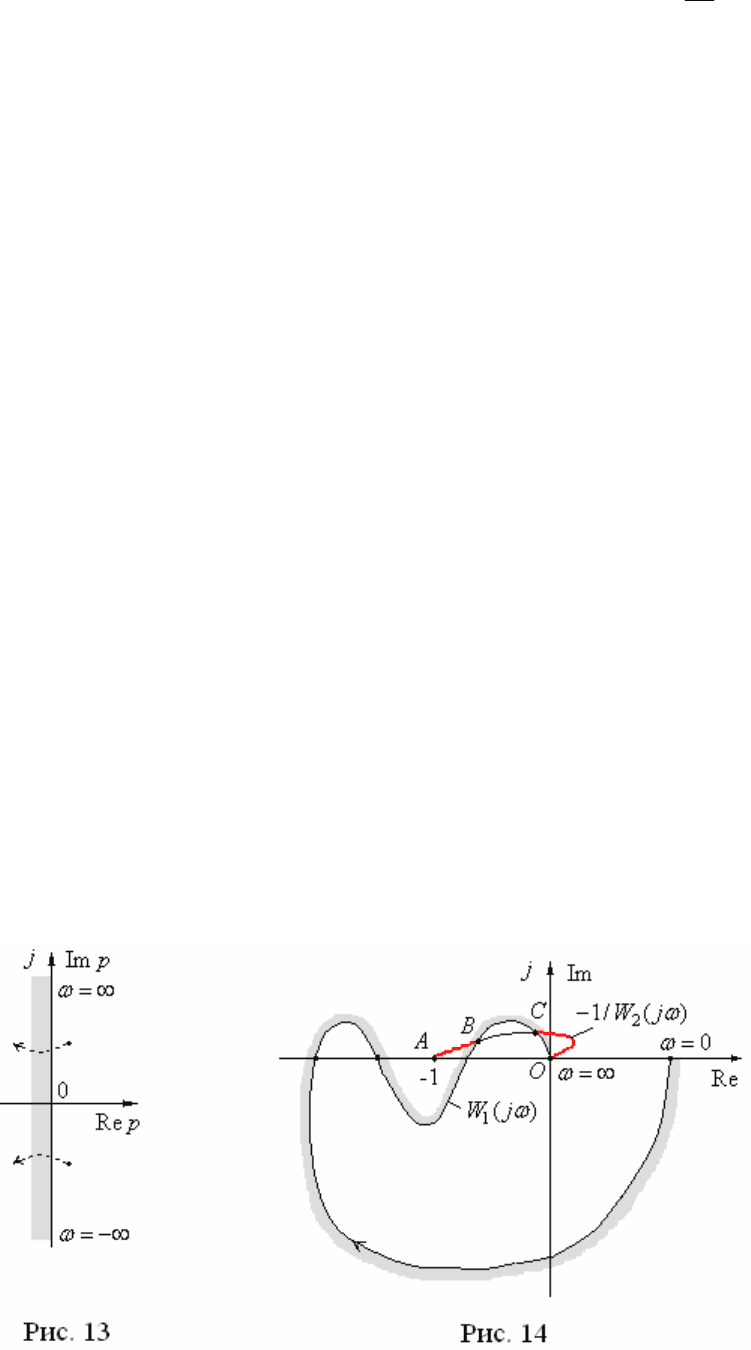
ложенные на мнимой оси. Заштрихуем мнимую ось
p j
плоскости корней
(рис. 13) и ее отображение АФЧХ
1
( )
W j
на другой комплексной плоскости
так, чтобы при возрастании частоты
от
до
эта штриховка была слева.
Учитывая симметричность АФЧХ
1
( )
W j
относительно вещественной оси,
126
можно рассматривать годограф
1
( )
W j
, построенный при изменении
от
0
до
(рис. 14). При этом точки
p
в левой (правой) полуплоскости преобразуются
в точки, лежащие слева (справа) от АФЧХ
1
( )
W j
.
Пусть при некоторых значениях параметров выполняется условие
2
( ) 1
W p
. Тогда разомкнутая система согласно формуле (2) имеет с учетом
знака
( )/2
N m l
охватов точки
( 1, 0)
j
, где
m
количество правых полюсов
передаточной функции
1
( )
W p
,
l
количество правых корней характеристиче-
ского уравнения замкнутой системы:
1
1 ( ) 0
W p
. Отсюда следует, что замк-
нутая система имеет
2
l m N
правых корней характеристического уравнения.
При измененных параметрах передаточной функции
2
( )
W p
построим
АФЧХ
2
1/ ( )
W j
и найдем точки пересечения с АФЧХ
1
( )
W j
(на рис. 14
точки
B
и
C
). Если пересечение осуществляется с незаштрихованной (с за-
штрихованной) стороны, то число правых корней замкнутой системы с переда-
точной функцией (7) уменьшается (увеличивается): на один в точках пересече-
ния
1
( 0)
W j
и
1
( )
W j
; на два в точке пересечения
1
( )
W j
при
0
(рис. 13).
При этом участкам АФЧХ
2
1/ ( )
W j
, для которых суммарное уменьшение
правых корней равно
l
, соответствуют значения параметров передаточной
функции
2
( )
W p
, обеспечивающих устойчивость замкнутой системы.
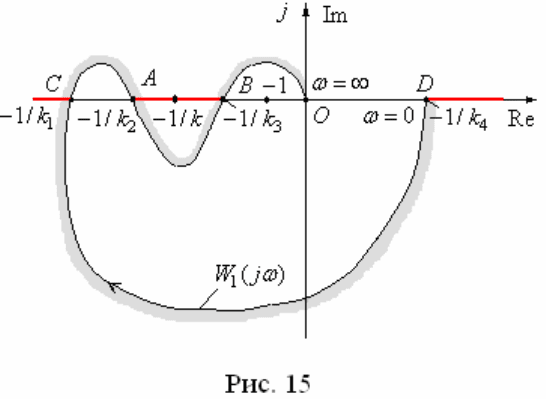
Рассмотрим также частный случай, когда
2
( )
W p k
. Пусть АФЧХ
1
( )
W j
имеет вид рис. 15 и значение
0
m
.
127
При
1
k
число охватов точки
( 1, 0)
j
равно
1
N
, поэтому замкнутая
система неустойчивая и имеет
0 2( 1) 2
l
правых корня.
При уменьшении коэффициента
k
точка
1/
k
пересекает АФЧХ
1
( )
W j
в точке
B
с незаштрихованной стороны при
0
. Следовательно, два правых
корня характеристического уравнения
1 ( ) 0
W p
переходят в левую полу-
плоскость.
При дальнейшем уменьшении коэффициента
k
пересечение происходит
в точке
A
с заштрихованной стороны при
0
и, следовательно, два левых
корня переходят в правую полуплоскость. Затем вновь после пересечения в
точке
C
два правых корня переходят в левую полуплоскость.
При увеличении коэффициента
k
и изменении его скачком от
до
точка
1/
k
пересекает АФЧХ
1
( )
W j
в точке
O
с незаштрихованной стороны
при
. Следовательно, один корень переходит в левую полуплоскость. При
дальнейшем увеличении коэффициента
k
пересечение происходит в точке
D
с
незаштрихованной стороны при
0
, т.е. еще один корень переходит в левую
полуплоскость.
Тем самым, область устойчивости замкнутой системы по коэффициенту
k
определяется интервалами
4
0
k k
,
1
0
k k
,
2 3
k k k
, лежащими со
стороны штриховки.
С учетом сказанного можно сформулировать интервальный критерий ус-
тойчивости Найквиста.
Для устойчивости замкнутой системы с отрицательной обратной связью
2
( )
W p
необходимо и достаточно, чтобы параметры передаточной функции
2
( )
W p
соответствовали интервалам АФЧХ
2
1/ ( )
W j
со стороны внешней
штриховки АФЧХ
1
( )
W j
, при переходе на которые из точки
( 1, 0)
j
сум-
марное уменьшение правых корней равнялось
l
, где
l
– число правых кор-
ней характеристического уравнения замкнутой системы при
2
( ) 1
W p
.
Отметим, что если замкнутая система неустойчивая при любом коэффи-
128
циенте усиления, то такая система называется структурно неустойчивой. На
рис. 6 приведен пример структурно неустойчивой системы.
Пример 1. Для передаточной функции разомкнутой системы
1 2
( )
( 1)( 1)
k
W p
p T p T p
(9)
найти условие устойчивости замкнутой системы по параметру
2
0
T
для задан-
ных значений
3
k
,
1
1
T
с.
Передаточную функцию
( )
W p
представим в виде произведения (7), где
1
1
( )
( 1)
k
W p
p T p
,
2
2
1
( )
1
W p
T p
.
Тогда в уравнении (7) будем иметь
1
2
( )
k
W j
j
,
2 2
1/ ( ) 1
W j jT
.
Обозначая
2
x
T
, построим график функции
1
jx
правой части при
изменении
x
от
0
до
. Изменяя
от
0
до
, построим график функции
1
( )
W j
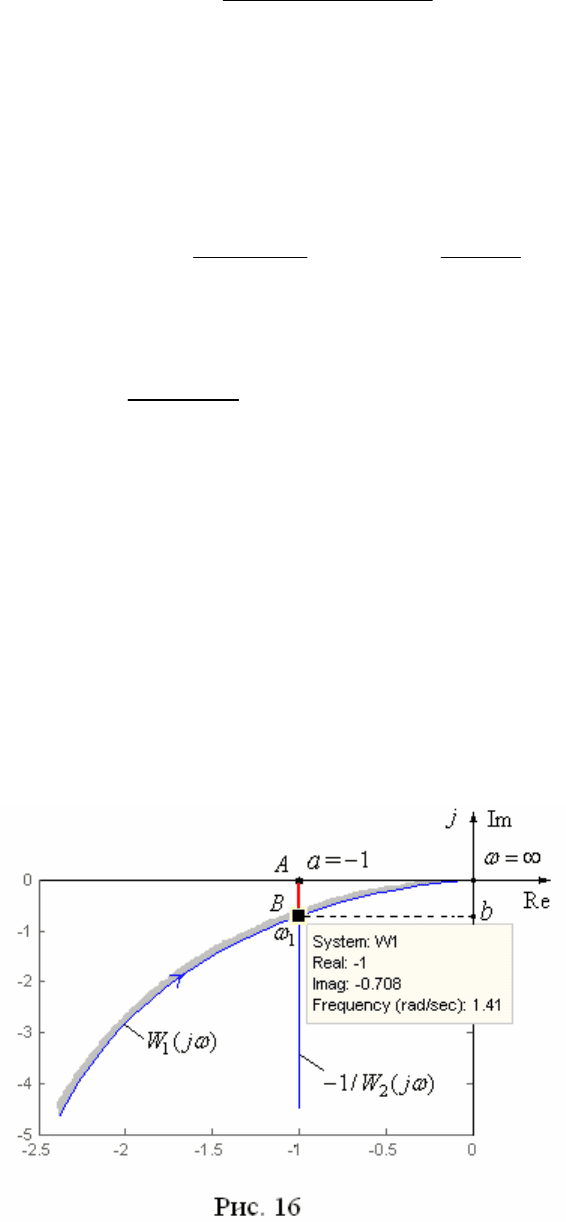
левой части. На рис. 16 приведены указанные графики, построенные с
помощью Script-файла:
k=3;T1=1;W1=tf([k],[T1 1 0]);
nyquist(W1,{0.5,25});hold on
x=0:0.1:25; W2=-1-i*x; u=real(W2); v=imag(W2);plot(u,v)
129
По АФЧХ
1
( )
W j
найдем частоту
1
1,41
рад/с, при которой происхо-
дит пересечение графиков.
Поскольку замкнутая система при
2
( ) 1
W p
устойчивая, то значение
0
l
. Поэтому область устойчивости определяется интервалом
AB
, располо-
женным со стороны штриховки. Полагая
11
( )
W j a jb
, где
1
a
,
0,708
b
, потребуем выполнения неравенства
2 1
T b
, при котором интер-
вал
AB
располагается со стороны штриховки. Отсюда найдем
2 1
/ 0,5
T b
.
Сравним полученный результат с критерием Гурвица, согласно которому
условие устойчивости замкнутой системы с передаточной функцией (9) имеет
вид:
2 1 1
/( 1) 0,5
T T T k
.
Таким образом, интервальный критерий Найквиста в отличие от обычно-
го критерия позволяет определять области устойчивости по параметрам систе-
мы.
Вопросы для самопроверки
1. В чем отличие критерия Найквиста от критерия Михайлова?
2. В каком диапазоне частот требуется строить АФЧХ разомкнутой системы
для определения устойчивости замкнутой системы?
3. В каком случае замкнутая система находится на границе устойчивости?
4. Какой смысл имеет частота среза?
5. Как применяется критерий Найквиста для разомкнутой системы, имеющей
корни на мнимой оси?
6. В чем заключается правило переходов Цыпкина?
7. Как определяются запасы устойчивости по АФЧХ разомкнутой системы?
8. Как влияет чистое запаздывание на устойчивость замкнутой системы?
9. Какая система называется структурно неустойчивой?
130
ЛЕКЦИЯ 11
Качество процессов автоматического регулирования. Прямые показатели качества.
Косвенные показатели качества: алгебраические, частотные, интегральные.
1. Качество процессов автоматического регулирования.
Для работоспособности системы помимо требования устойчивости
предъявляются определенные требования к качеству процессов автоматическо-
го регулирования. Под качеством САР понимается совокупность требований к
процессу регулирования для выбранной выходной координаты.
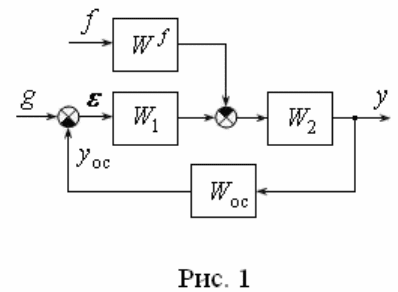
Рассмотрим обобщенную структурную схему, представленную на рис. 1.
Здесь выходной сигнал
( )
y t
повторяет вид входного сигнала
( )
g t
при
действии ограниченного возмущения
( )
f t
таким образом, чтобы ошибка
ос
( ) ( ) ( )
t g t y t
была ограниченной. Если, например,
ос ос
( )
W p k
, то
ос
( ) ( ) ( )
t g t k y t
и, следовательно, скорость выходного сигнала
( )
y t
при
lim ( ) 0
t
t
не совпадает со скоростью входного сигнала
( )
g t
. Если
ос
( ) 1
W p
,
то выход
( )
y t
отслеживает вход
( )
g t
.
При произвольных входных сигналах
( )
g t
,
( )
f t
качество САР удобно
оценивать по ошибке
ос
( ) ( ) ( )
t g t y t
. Если входные сигналы
( )
g t
,
( )
f t
по-
стоянные, то можно оценивать качество САР по выходу
( )
y t
.
Движение
( )
t
или
( )
y t
содержит переходное и установившееся движе-
ние. Переходное движение зависит от начальных условий, вызванных, в том
