Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics
Подождите немного. Документ загружается.


8 Sign-Invariants and Exact Solutions 403
yields the following parabolic PDE:
˜
P[v] ≡ v
t
−
˜ϕ(v)v
xx
+ (av + b)(v
x
)
2
+
˜
f (v)
= 0, with (8.84)
˜
H[v] = v
t
−
(av + b)(v
x
)
2
+
˜
M(v)
. (8.85)
Denoting for convenience
G(v) =
˜
f (v)−
˜
M(v)
˜ϕ(v)
, (8.86)
equations (8.76) and (8.77) are translated into
˜
M
− (av + b)G
− 5aG = 0, (8.87)
G
˜
M − G
˜
M
+ 2(av + b)G
2
= 0, (8.88)
respectively. The last ODE (8.88) can be integrated to give
˜
M(v) = 2P(v)G(v), (8.89)
where P(v) is a quadratic polynomial
P(v) =
1
2
av
2
+ bv + c. (8.90)
Substituting (8.90) into (8.87) yields the following linear hypergeometric ODE for
the function G in (8.86):
(av
2
+ 2bv + 2c)G
+ 3(av + b)G
− 3aG = 0, (8.91)
which plays a key role in the further construction of sign and zero-invariants for
our parabolic problem. We call (8.91) the generating equation, since actually, by
formulae (8.86) and (8.83), it generates the coefficients in the parabolic PDE (8.80)
and operator (8.81). In particular, (8.84) and (8.85) imply the following result.
Proposition 8.20
Under the given notation, the sign-invariant of
(8.84)
is
˜
H
∗
[v] = v
xx
+ G(v), (8.92)
where
G
is an arbitrary solution of the ODE
(8.91)
.
Unfortunately (8.91) cannot be solved explicitly in general. Below we use its par-
ticular solutions.
8.4.2 Exact solutions
Since, by Proposition 8.20, operator (8.92) is a zero-invariant of (8.84) with G satis-
fying (8.91), it is seen that, for an arbitrary solution v(x, t) of (8.84),
v
xx
+ G(v) = 0forx ∈ IR , t > 0, (8.93)
if the same is valid for t = 0. Of course, operator (8.85) is also a zero-invariant, i.e.,
in view of (8.86) and (8.89),
v
t
= P
(v)(v
x
)
2
+ 2P(v)G(v) for t > 0. (8.94)
Then(8.93)and (8.94) yield exactsolutionsofthe PDE (8.84).Let a givensolution
G(v) of (8.91) be well-defined in a neighborhoodof v = 1. Set
Y (v) =
v
1
G(η) dη.
© 2007 by Taylor & Francis Group, LLC
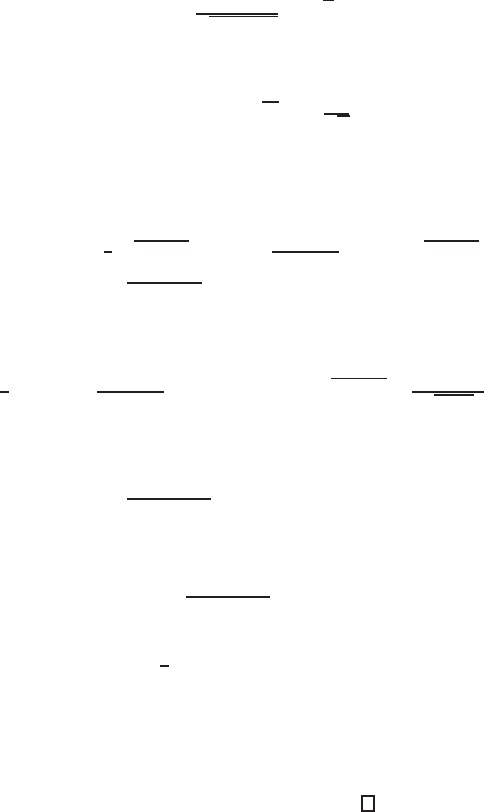
404 Exact Solutions and Invariant Subspaces
It follows from (8.91) that Y solves the linear ODE
B[Y ] ≡ 2PY
+ 3P
Y
− 3P
Y
= 0. (8.95)
Multiplying (8.93) by v
x
, and integrating over (0, x) yields
(v
x
)
2
= 2[B(t) − Y (v)], (8.96)
where B(t) is a smooth function to be determined later.
Theorem 8.21
Let
G
be a solution of
(8.91)
such that
Y (v)
exists. Then the quasi-
linear equation
(8.84)
admits the explicit solution
v(x , t)
given by
v(x ,t)
1
dz
√
B(t )−Y (z)
=
√
2 x + C(t), (8.97)
where the functions
B(t)
and
C(t)
satisfy the dynamical system
B
= 4aB
2
+ α
1
B + α
2
,
C
= α
3
√
B + α
4
1
√
B
,
(8.98)
α
1
= 4P(1)G
(1) + 2P
(1)G(1), α
2
= 2P(1)G
2
(1),
α
3
= 2P
(1), α
4
= 2P(1)G(1).
Proof. Integrating (8.96) again yields (8.97). Differentiating (8.97) with respect to t
and x implies
v
t
=
1
2
√
S(t,v)B
(t)
v
1
dz
[S(t,z)]
3/2
+ C
(t)
√
S(t,v),
v
x
=
√
2[S(t,v), where S(t,v) = B(t) − Y (v).
(8.99)
Plugging (8.96) and (8.99) into (8.94), we obtain the identity with respect to v and t,
which are treated here as the independent variables,
1
2
B
(t)
v
1
dz
[S(t,z)]
3/2
+ C
(t) ≡ 2P
(v)
S(t,v)+
2P(v)G(v)
√
S(t,v)
. (8.100)
Setting v = 1 yields the second ODE in (8.98). Then, differentiating (8.100) with
respect to v, and multiplying by S
3/2
gives
B
(t)−2PG
2
2S
= 2P
S + 2PG
+ P
G. (8.101)
It follows from the first ODE (8.98) that (8.101) is valid identically for v = 1.
Differentiating (8.101) again and using equation (8.91) yields
B
(t)−2PG
2
2S
v
= 2P
G.
Finally, the identity holds,
2aB
2
−
1
2
B
+ J
1
[v]B + J
2
[v] ≡ 0, where (8.102)
J
1
[v] = 2PY
+ P
Y
− 4P
Y, and
J
2
[v] =−2PYY
+ P(Y
)
2
− PYY
+ 2P
Y
2
.
It is easy to see that, by (8.95), J
1
= B[Y ] = 0andJ
2
=−Y B[Y ] = 0. Hence,
J
1
and J
2
are constants, J
1
[v] ≡ J
1
(1) and J
2
[v] ≡ J
2
(1). Then (8.102) is exactly
equation (8.98) for B(t). This completes the proof.
We next describe solutions, corresponding to some particular G satisfying (8.91).
© 2007 by Taylor & Francis Group, LLC

8 Sign-Invariants and Exact Solutions 405
Example 8.22 (Quasilinear parabolic PDEs)Foranyfixed a, b∈ IR , the hyper-
geometric equation (8.91) has the linear solution
G(v)= P
(v)= av+ b.
Then (8.93) has the form
v
xx
+ av+ b= 0forx∈ IR, t > 0. (8.103)
Let a > 0. Integrating (8.103) yields
v(x, t)=−
b
a
+ C
1
(t) cos(λx)+ C
2
(t) sin(λx), (8.104)
whereλ=
√
a. Substituting (8.104) into the Hamilton–Jacobi PDE (8.94),
v
t
=(av+ b)
(v
x
)
2
+(av
2
+ 2bv+ 2c)
,
we derive the following cubic DS for the coefficients{C
1
, C
2
}:
C
1
= [a
2
(C
2
1
+ C
2
2
)+ 2ac]C
1
,
C
2
= [a
2
(C
2
1
+ C
2
2
)+ 2ac]C
2
,
(8.105)
possessing blow-up solutions. This determines exact solutions (8.104) of the follow-
ing quasilinear heat equation (cf. (8.84)):
v
t
= D[v] ≡˜ϕ(v)v
xx
+ (av + b)(v
x
)
2
+(av + b)
˜ϕ(v) + av
2
+ 2bv + 2c
,
(8.106)
where ˜ϕ(v) ≡ ϕ(E(v)) ≥ 0 is arbitrary. For solutions u(x, t) = E(v(x , t)),where
E is given by (8.82), there occurs the PDE
u
t
= ϕ(u)u
xx
+ [aE
−1
(u) + b]
×
ϕ(u) + a(E
−1
(u))
2
+ 2bE
−1
(u) + 2c
E
(E
−1
(u)),
which can easily be rewritten in the divergent form (8.1).
Example 8.23 (Semilinear heat equations) Consider
u
t
= u
xx
+
α R(u)+β
R
(u)
, (8.107)
where R(u) satisfies the following nonlinear ODE:
R
= exp
−
aR
2
2
− bR − c
. (8.108)
The SI is
H[u] = u
t
− (aR + b)R
(u
x
)
2
−
α R(u)+β
R
(u)
, (8.109)
which is also a zero-invariant of (8.107). To calculate the corresponding solutions,
we set u = E(v) in (8.107), where E(v) = R
−1
(v),toderive
v
t
= F[v] ≡ v
xx
+ (av + b)(v
x
)
2
+ αv + β. (8.110)
Obviously, operator F admits the 2D subspace of linear functions W
2
= L{1, x}.
Hence, the solutions of (8.110) are
v(x , t) = C
1
(t) + C
2
(t)x ∈ W
2
,
© 2007 by Taylor & Francis Group, LLC

406 Exact Solutions and Invariant Subspaces
C
1
= aC
1
C
2
2
+ bC
2
2
+ αC
1
+ β,
C
2
= aC
3
2
+ αC
2
,
where the DS can be integrated. Adding the term −v
xxxx
to the right-hand side of
(8.110) gives a fourth-orderparabolic PDE, which admits the same explicit solutions
but, of course, makes the SI (8.109) nonexistent.
Example 8.24 Setting ˜ϕ(u) ≡ 1, b = 0 in (8.106) yields
u
t
= u
xx
+
a
2
R
3
(u)+a(2c+1)R(u)
R
(u)
,
where R(u) is given by (8.108) with a = 0andb = 0. It admits the SI
H[u] = u
t
− aRR
(u
x
)
2
−
a
2
R
3
+2acR
R
.
In order to find explicit solutions, setting u = R
−1
(v) gives
v
t
= F
1
[v] ≡ v
xx
+ av(v
x
)
2
+ a
2
v
3
+ a(2c + 1)v. (8.111)
Assume that a > 0, and set λ =
√
a.OperatorF
1
of this PDE admits the 1D
subspace W
1
= L{cos(λx)}. Thus, setting v(x, t) = C(t) cos(λx ) ∈ W
1
yields
C
= a
2
C
3
+ 2acC.
If a < 0, the subspace is W
1
= L{cosh(λx)}, with λ =
√
|a|.
As we have shown in Chapter 1, operator F
1
in (8.111) admits a more general 2D
subspace
W
2
= L{cos(λx), sin(λx)}, (8.112)
that does not give new exact solutions of (8.111) because of its translational invari-
ance with respect to x . For higher-order evolution PDEs, e.g., for the hyperbolic one
v
tt
= F
1
[v], (8.113)
using subspace (8.112) yields new solutions via
v(x , t) = C
1
(t) cos(λx) + C
2
(t) sin(λx ) ∈ W
2
,
C
1
= [a
2
(C
2
1
+ C
2
2
) + 2ac]C
1
,
C
2
= [a
2
(C
2
1
+ C
2
2
) + 2ac]C
2
.
Example 8.25 (Fourth-order KS-type equation) There are easy extensions to
higher-order PDEs (the SIs are lost). For instance, the fourth-order semilinear KS-
type equation with cubic nonlinearities
v
t
=−v
xxxx
+ α
v(v
x
)
2
+ v
3
+ βv
admits the explicit solution
v(x , t) = C(t) cos x, with C
= αC
3
+ (β − 1)C.
Example 8.26 (KdV-type equation) Thethird-orderPDEwiththe same cubicnon-
linearities
v
t
= v
xxx
+ α
v(v
x
)
2
+ v
3
+ βv
© 2007 by Taylor & Francis Group, LLC
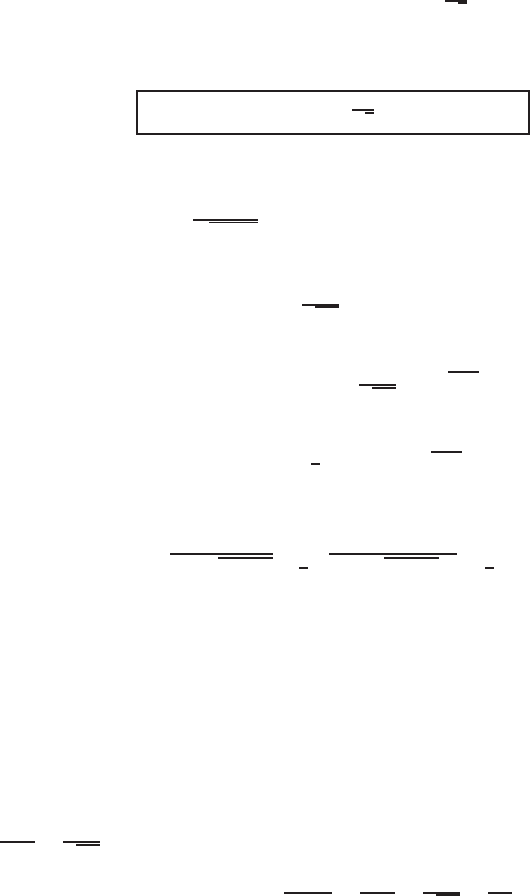
8 Sign-Invariants and Exact Solutions 407
has the periodic soliton-type solution
v(x , t) = C(t) cos(x −t), where C
= αC
3
+ βC.
Example 8.27 (Quasilinear heat equations) Let us return to SIs for the quasilinear
parabolic PDEs. In this example, we consider the generating equation (8.91) in the
case where a = c = 0andb = 1. Then,
2vG
+ 3G
= 0 ⇒ G(v) =
α
√
v
+ β, (8.114)
where α = 0andβ are free constants. It follows from (8.86), (8.89), and (8.114) that
the corresponding PDE (8.84) is
v
t
=˜ϕ(v)v
xx
+ (v
x
)
2
+
α
√
v
+ β
[ ˜ϕ(v) + 2v]. (8.115)
Exact solutions of (8.115) have been given in Theorem 8.21. The corresponding
original equation (8.73) for u = E(v) is now
u
t
= ϕ(u)u
xx
+
α
√
E
−1
(u)
+ β
ϕ(u) + 2E
−1
(u)
E
(E
−1
(u)). (8.116)
In the case where ˜ϕ = 1, setting v = ln u yields the semilinear heat equation
u
t
= u
xx
+ u
α
√
lnu
+ β
(1 + 2lnu), (8.117)
possessing the above solutions u = e
v
.Forα = 1andβ = 0, we find
u
t
= F
2
[u] ≡ u
xx
+ u
1
√
lnu
+ 2
√
lnu
, (8.118)
which admits the following SI:
H[u] = u
t
−
1
u
(u
x
)
2
− 2u
√
lnu. (8.119)
Since(8.119)is also a zero-invariantof (8.118),we obtainsolutionsu(x, t) = e
v(x ,t)
,
where v(x, t) solves the algebraic equation
t
t −
√
v(x , t) −
1
3
[t −
√
v(x , t) ]
3
=
1
2
x . (8.120)
For α = 0, (8.117) gives the well-known equation reduced to the PDE
u
t
= u
xx
+ u lnu,
possessing a 4D symmetry Lie algebra [10, p. 135]; see also Example 9.9 for more
details. For α = 0, (8.117) does not have any extra group symmetries.
Example 8.28 (On higher-order extensions) It is easy to derivehigher-ordermod-
els possessing precisely the same exact solutions, though some PDEs can be rather
artificial. The simple rules of construction are as follows. For instance, using the
zero-invariant (8.119) in the PDE (8.118) yields that, for exact solutions, u
xx
=
(u
x
)
2
u
−
u
√
lnu
, and, on differentiation,
u
xxx
= F
3
[u] ≡
2u
x
u
xx
u
−
(u
x
)
3
u
2
−
u
x
√
lnu
+
u
x
lnu
.
© 2007 by Taylor & Francis Group, LLC
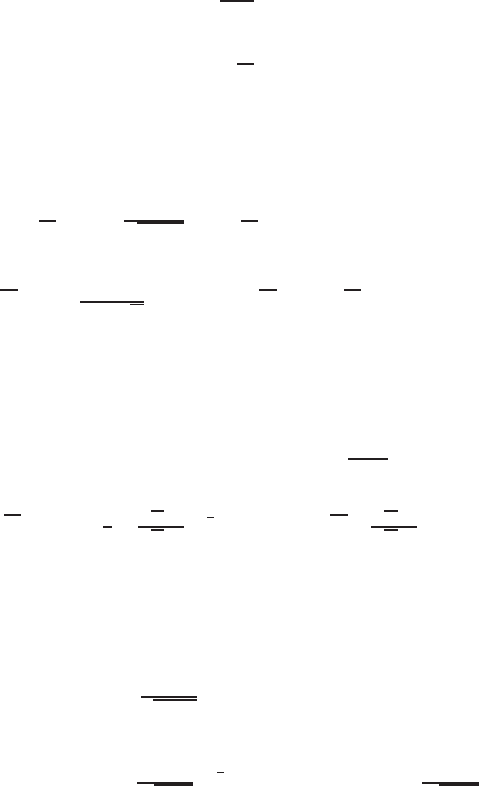
408 Exact Solutions and Invariant Subspaces
Obviously, the third-order PDE
u
t
= ψ(u, ...)(u
xxx
− F
3
[u]) + F
2
[u],
where ψ(u, ...) is an arbitrary function, admits the same solutions u = e
v
given by
(8.120). One can reconstruct other, less artificial versions of such PDEs. Similarly,
calculating u
xxxx
denoted again by F
3
[u] yields a fourth-order PDE, etc.
Example 8.29 (Quasilinear parabolic PDEs) We return to quasilinear heat equa-
tions and determine other exact solutions and SIs. Recall that function E given by
(8.78) (it transforms (8.116) into (8.73), and eventually into (8.1) with N = 1) is
determined from (8.79) and (8.82), so
E
=
E
ϕ(E)
. (8.121)
Consider first the coefficient
ϕ(u) =
1
2u
. (8.122)
Then (8.121) yields
E
= 2EE
, (8.123)
and there exist two possibilities.
(i) Take E(v) = tanv. Substituting E into (8.116) yields
u
t
=
1
2u
u
xx
+
α
√
tan
−1
u
+ β
1
2u
+ 2tan
−1
u
(1 + u
2
).
Here, setting u
2
= U, we arrive at
U
t
= (
√
U )
xx
+
α
tan
−1
√
U
+ β
1 + 4
√
U tan
−1
√
U
(1 + U), (8.124)
which has solutions
U(x , t) = tan
2
v(x , t),
where v(x, t) is given in Theorem 8.21. The equation (8.69) is (8.124), with α =
β = 1.
(ii) Take another solution of the ODE (8.123), E(v) =−
e
2v
+1
e
2v
−1
. Setting u
2
= U in
(8.116) yields
U
t
= (
√
U )
xx
+
α
1
2
ln
√
U −1
√
U +1
−
1
2
+ β
1 + 2
√
U ln
√
U −1
√
U +1
(U − 1),
which admits solutions U(x, t) = E
2
(v(x, t)).
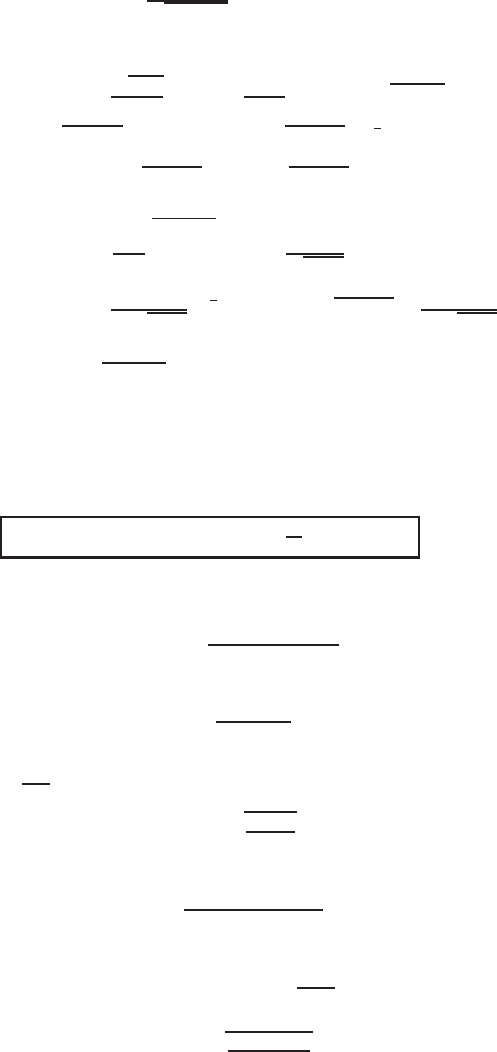
(iii) If we take, for instance,
ϕ(u) = cos
2
u, (8.125)
then (8.121) admits the solution E(v) = sin
−1
e
v
. Then (8.116) has the form
u
t
= cos
2
uu
xx
+
α
√
lnsinu
+ β
cos
2
u + 2lnsinu
tanu.
Setting tanu = U yields the quasilinear heat equation
U
t
=
tan
−1
U
xx
+
α
ln
U
√
1+U
2
−
1
2
+ β
1 + 2(1 +U
2
) ln
U
√
1+U
2
U,
© 2007 by Taylor & Francis Group, LLC
8 Sign-Invariants and Exact Solutions 409
which has the solution U(x, t) =
e
v(x,t)
√
1−e
2v(x,t)
, with v(x , t) given in Theorem 8.21.
It is easy to find other coefficients ϕ(u) such that (8.121) admits a simple function
E(v) determining solutions of the corresponding quasilinear equation (8.116).
(iv) For instance, for ϕ(u) =
√
1+u
2
u
, E(v) =
e
2v
−1
2e
v
,andU =
√
1 + u
2
,wefind
U
t
=
√
U
2
− 1
xx
+
α
ln
U +
√
U
2
− 1
−
1
2
+ β
×
U +2
√
U
2
− 1ln
U +
√
U
2
− 1
,
possessing the solution U(x , t) =
e
2v(x,t)
+1
2e
v(x,t)
.
(v) In the case where ϕ(u) =
1
cosu
, E(v) = 2sin
−1
e
v
√
1+e
2v
,andU = sin u,wehave
U
t
=
sin
−1
U
xx
+
α
ln
U
1+
√
1−U
2
−
1
2
+ β
1 + 2
√
1 − U
2
ln
U
1+
√
1−U
2
U
with the solution U(x , t) =
2e
v(x,t)
e
2v(x,t)
+1
.
Example 8.30 Consider now the last case a = 1andb = c = 0, so (8.91) is
v
2
G
+ 3vG
− 3G = 0,
with the general solution G(v) = αv + βv
−3
. From (8.86) and (8.89), we have, by
Theorem 8.21, that the parabolic equation (8.84),
v
t
=˜ϕ(v)v
xx
+ v(v
x
)
2
+ (αv +β
1
v
3
)[ ˜ϕ(v) + v
2
],
possesses such exact solutions. Setting v = R(u),whereR solves (8.108) (R is the
inverse function to E given by (8.79)), yields the quasilinear heat equation
u
t
= ϕ(u)u
xx
+
(α R
4
+β)(ϕ(u)+R
2
)
R
3
R
.
In the case where ϕ(u) ≡ 1, α = 0, and β = 1, this reduces to
u
t
= u
xx
+
1+R
2
(u)
R
3
(u)R
(u)
,
where R(u) is given by (8.108) with a = 1, b = c = 0, and the SI is H[u] =
u
t
− RR
(u
x
)
2
−
1
RR
. In particular, there exists the solution
R(u(x, t)) =
4t
2
−x
2
2t
.
If ϕ(u) ≡ 1andα = β = 1, we arrive at the PDE
u
t
= u
xx
+
(R
4
(u)+1)(1+R
2
(u))
R
3
(u)R
(u)
,
where R is given above, with the SI
H[u] = u
t
− RR
(u
x
)
2
−
R
4
+1
RR
and the solution
R(u(x, t)) =
sin4t +sin2x
cos4t
.
© 2007 by Taylor & Francis Group, LLC

410 Exact Solutions and Invariant Subspaces
In the particular quasilinear case of (8.122), setting u
2
= U yields
U
t
=
√
U
xx
+
(α R
4
+β)(1+2
√
UR
2
)
R
3
R
(here R = R(
√
U)), which admits solutions U (x, t) = E
2
(v(x, t)),wherev is given
in Theorem 8.21. In the case of (8.125), setting tanu = U gives
U
t
= (tan
−1
U)
xx
+
(α R
4
+β)[1+(1+U
2
)R
2
]
R
3
R
,
with R = R(tan
−1
U), and the solution is U(x , t) = tan E(v(x , t)).
8.5 General first-order Hamilton–Jacobi sign-invariants
In this section, we perform a more general and detailed analysis of first-order SIs for
the quasilinear heat equation
u
t
= ψ(u)u
xx
+ q(u) in IR × IR
+
, (8.126)
where ψ(u) ≥ 0andq(u) are given smooth functions. For convenience, let us per-
form a smooth transformation u = (v) to obtain the PDE
v
t
= ϕ(v)v
xx
+ m(v)(v
x
)
2
+ f (v), (8.127)
with ϕ(v) ≥ 0. We will deal with a more general (than in Section 8.4) quadratic
Hamilton–Jacobi operator of the form
H[v] = v
t
− H [v] ≡ v
t
−
m(v)(v
x
)
2
+ s(v)v
x
+ M(v)
, (8.128)
with three free coefficients m, s,andM. Without loss of generality, in (8.128),we set
the coefficient of (v
x
)
2
to be equal to m(v), which is the same function, as in (8.127).
In terms of the original solutions u(x , t), the SI has a similar form
˜
H[u] = u
t
−
h
2
(u)(u
x
)
2
+ h
1
(u)u
x
+ h
0
(u)
.
Our goal is to show that more general SIs (8.127) provide us with extra exact solu-
tions and yield other possibilities to derive estimates of solutions.
It is convenient to perform basic calculations for the new coefficients
g(v) =−
s(v)
ϕ(v)
and G(v) =
f (v)−M(v)
ϕ(v)
. (8.129)
As in the previous section, P(v) is the quadratic polynomial (8.90), P(v) =
1
2
av
2
+
bv + c. We next state the first main result on the existence of the SI.
Theorem 8.31
Operator
(8.128)
is a sign-invariant of the PDE
(8.127)
if the coeffi-
cients
g(v)
and
G(v)
satisfy the following system of ODEs:
2Pg
+ 3P
g
− 8P
g = 0, (8.130)
2PG
+ 3P
G
− 3P
G =
2
3
(Pg
2
)
, (8.131)
and other coefficients are given by
m = P
, s
=
2
3
(2P
g + Pg
),
and
M = 2PG. (8.132)
© 2007 by Taylor & Francis Group, LLC
8 Sign-Invariants and Exact Solutions 411
The linear ODEs (8.130) and (8.131) are of the hypergeometric type. The second
equation is non-homogeneous and its right-hand side depends on the solutions of
the first equation. Theses are the generating equations, which determine the class of
parabolic PDEs under consideration. As the next step, let us find the representation
of the corresponding exact solutions, since by Theorem 8.31, the operator (8.128) is
also a zero-invariant of (8.127), i.e.,
H[v] = 0forallt > 0, if H[v] = 0fort = 0.
For fixed constants B and C,letv = V (x ; B, C) be the solution of the Cauchy
problem for the ODE
v
xx
+ g(v)v
x
+ G(v) = 0forx > 0, with v(0) = B,v
(0) = C. (8.133)
We assume that this ODE is locally well-posed for arbitrary B, C ∈ IR . The equation
(8.133) is associated with the PDE (8.127) and with the corresponding Hamilton–
Jacobi equation
H[v] = 0, (8.134)
in the sense that, altogether, these three equations are linearly dependent. Clearly,
the stationary, time-independent equation (8.133) reduces to a first-order one and
sometimes can be integrated in quadratures. We will present such examples below.
The simpler case g = 0, for which (8.133) is always integrated in quadratures, was
studied in the previous section, where a different general structure of exact solutions
is derived. Finite-dimensional dynamics of exact solutions is as follows:
Theorem 8.32
Under hypotheses of Theorem
8.31
, the set of solutions
{v(x , t) =
V (x; B(t), C(t))}
via zero-invarianceof operator
(8.128)
is governed by the follow-
ing second-order dynamical system for coefficients
B(t)
and
C(t)
:
B
= P
(B)C
2
+ s(B)C + 2P(B)G(B),
C
= P
(B)C
3
+ [s
(B) − 2P
(B)g(B)]C
2
+[2P(B)G
(B) − s(B)g(B)]C − s(B)G(B).
(8.135)
The stationary equation (8.133) defines an evolutionary invariant set M of the
parabolic flow induced by (8.127), in the sense that
v(·, 0) ∈ M ⇒ v(·, t) ∈ M for t > 0.
The DS (8.135) is the parabolic PDE (8.127) restricted to the set M.
8.5.1 Proofs of main theorems
Proposition 8.33
Operator
(8.128)
is a sign-invariantof the equation
(8.127)
iff the
coefficients satisfy the system
m
= 0, (8.136)
I
1
(v) ≡ s
− 4m
g − g
m = 0, (8.137)
I
2
(v) ≡ M
− 2gs
− 5m
G − mG
+ 2mg
2
= 0, (8.138)
I
3
(v) ≡−3s
G + g
M + 4mgG = 0, (8.139)
© 2007 by Taylor & Francis Group, LLC

412 Exact Solutions and Invariant Subspaces
I
4
(v)≡−
M
G
+ 2m= 0. (8.140)
Proof. Set, as usual, J= H[v]. Differentiating this equality with respect to t,
J
t
=v
tt
−(H[v])
t
,
substituting the second derivativev
tt
from (8.127) differentiated in t, and evaluating
other lower-order ones,v
t
,v
tx
andv
txx
, we arrive at the parabolic PDE
J
t
= M[J]+ F, (8.141)
where M is a linear second-order operator that is elliptic in the parabolicity domain
of (8.127). By (8.136)–(8.140), the lower-order term is trivial,
F=ϕ
m
(v
x
)
4
+ I
1
(v
x
)
3
+ I
2
(v
x
)
2
+ I
3
v
x
+ I
4
G
2
≡ 0. (8.142)
Hence, J solves the homogeneous linear parabolic PDE
J
t
= M[J],
and the result follows from the MP. If F≡ 0 in (8.141), then obviously at least one
sign of (8.128) cannot be preserved with time on the corresponding set of solutions
(the proof is by direct constructing suitable initial data).
Remark 8.34 Consider the identity (8.142) as a fourth-order algebraic equation for
v
x
, meaning that the set{1,v
x
,(v
x
)
2
,(v
x
)
3
,(v
x
)
4
} is linearly dependent. Therefore,
there exists the representation v
x
= R(v) and, on integration, this kind of zero-
invariance gives
dv
R(v)
= x+ C(t).
Plugging into (8.127) gives the elementary ODE C
= constant, which leads to the
standard traveling wave solution v(x, t)=θ(x−λt). Therefore, in order to obtain
a nontrivial result in the proof, we must assume that all the five terms in (8.142) are
linearly independent and this gives the five ODEs (8.136)–(8.140).
Proof of Theorem 8.31. Equation(8.136)defines linear functions m(v) = av +b ≡
P
(v);cf.thefirst equation (8.132). It follows from (8.140) that
M
G
= 2
m(v) dv≡ 2P(v); (8.143)
cf. the third equation (8.132). Substituting M from (8.143) into (8.139) yields
3s
− 4P
g − 2Pg
= 0, (8.144)
and the second equation (8.132) follows. The system of ODEs (8.137), (8.144) gives
the first generating equation (8.130). Finally, the second one, (8.131), is the result of
substituting M from (8.143) and s
from (8.144) into (8.138).
Proof of Theorem 8 .32. Setting x = 0 in (8.134) and in v
xt
= (H [v])
x
, and using
(8.133), (8.132) yields the DS (8.135).
8.5.2 P(v) is linear polynomial: exact solutions
General structure of SIs. Here, we study the SIs in the linear case a = 0, where
the quadratic polynomial is P(v) = bv + c with b = 0. Set c = 0, corresponding
© 2007 by Taylor & Francis Group, LLC
