Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics
Подождите немного. Документ загружается.

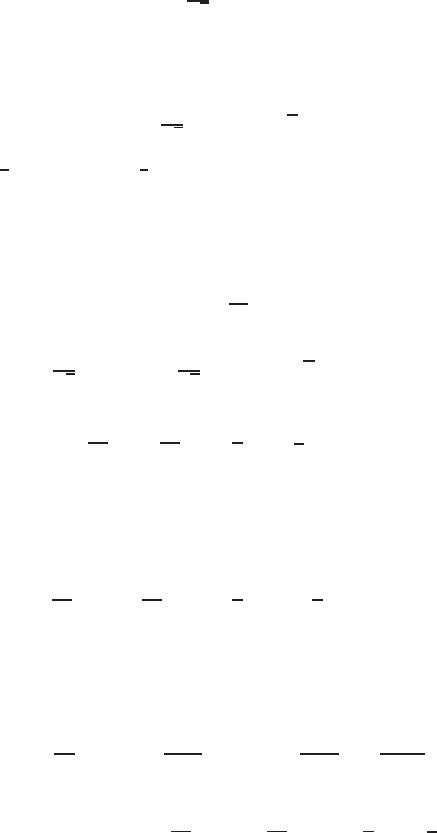
8 Sign-Invariants and Exact Solutions 413
to translation. Moreover, it follows from the generating ODEs (8.130) and (8.131)
that the constant b does not play any role in the analysis, so we set b = 1. Therefore,
consider (8.130) and (8.131) with the linear function
P(v) = v. (8.145)
The first equation (8.130) is then easily integrated:
g(v) = µ
1
√
v
+ ν(v>0), (8.146)
with arbitrary constants µ and ν.
Let us begin with a simpler case ν = 0 and consider the critical case ν = 0 later
on. Substituting (8.146) into the right-hand side of (8.131) yields
G(v) = α
1
√
v
+ β + K
1
√
v + K
2
v, (8.147)
where K
1
=
2
3
µν and K
2
=
2
9
ν
2
. Next, using the general solutions (8.146) and
(8.147) of the generating ODEs, we will study the structure of the evolutionary in-
variant set given by the stationary equation (8.133) and the DS (8.135).
Linearization of the stationary equation. This consists of a few steps.
(i) Set
v =
1
w
2
(8.148)
in the ODE
v
xx
+
µ
1
√
v
+ ν
v
x
+ α
1
√
v
+ β + K
1
√
v + K
2
v = 0 ⇒
ww
xx
− 3(w
x
)
2
+ (µw + ν)ww
x
−
K
2
2
w
2
−
K
1
2
w
3
−
β
2
w
4
−
α
2
w
5
= 0.
(8.149)
(ii) Set
w = z
x
, (8.150)
so that (8.149) reads
z
x
z
xxx
− 3(z
xx
)
2
+ (µz
x
+ ν)z
x
z
xx
−
K
2
2
(z
x
)
2
−
K
1
2
(z
x
)
3
−
β
2
(z
x
)
4
−
α
2
(z
x
)
5
= 0.
(8.151)
(iii) We now introduce the inverse function with respect to the space variable
x = (y, t) ≡ z
−1
(y, t), (8.152)
so that z((y, t), t) ≡ y,and
z
x
=
1
y
, z
xx
=−
yy
(
y
)
3
, z
xxx
=−
yyy
(
y
)
4
+ 3
(
yy
)
2
(
y
)
5
.
Plugging these derivatives into (8.151) yields
yyy
+ (µ + ν
y
)
yy
+
K
2
2
(
y
)
3
+
K
1
2
(
y
)
2
+
β
2
y
+
α
2
= 0.
(iv) Let
y
= V. (8.153)
© 2007 by Taylor & Francis Group, LLC

414 Exact Solutions and Invariant Subspaces
Then V solves
V
yy
+ (µ + νV )V
y
+
K
2
2
V
3
+
K
1
2
V
2
+
β
2
V +
α
2
= 0. (8.154)
(v) Finally, let us apply the transformation (used in hyperelliptic function theory
since the nineteenth century)
V = κ
ρ
y
ρ
(8.155)
to obtain an equation with cubic nonlinearities,
ρ
2
ρ
yyy
+ µρ
yy
+
β
2
ρ
y
+
α
2κ
ρ
+(νκ − 3)
ρρ
y
ρ
yy
+
1
9
(νκ − 6)(ρ
y
)
3
+
µ
3
ρ(ρ
y
)
2
= 0.
Therefore, choosing in (8.155)
κ =
3
ν
(8.156)
gives the linear ODE
ρ
yyy
+ µρ
yy
+
β
2
ρ
y
+
αν
6
ρ = 0. (8.157)
The characteristic equation is derived by substituting ρ = e
λy
,
λ
3
+ µλ
2
+
1
2
βλ +
1
6
αν = 0. (8.158)
At last, the general solution takes the form
ρ(y) = H
1
ρ
1
(y) + H
2
ρ
2
(y) + H
3
ρ
3
(y),
where ρ
1
, ρ
2
,andρ
3
are linearly independent solutions of the ODE (8.157). In view
of the representation (8.155) of the solution V ,wemaysetH
1
= 1. The trivial
choice H
1
= 0 leads to a significant simplification of the solution. We write the
general solution of (8.157) in the form of
ρ(y) = ρ
1
(y) + H
2
ρ
2
(y) + H
3
ρ
3
(y). (8.159)
Linearization of (8.127). Consider (8.128), where the coefficients are constructed
from (8.132) with the functions (8.145)–(8.147). This yields
m(v) = 1, s(v) = 2µ
√
v +
4
3
νv + K
3
, M(v) = 2v G(v),
where K
3
is a free constant. The rest of the coefficients of the quasilinear equation
(8.127) are obtained from (8.129),
ϕ(v) =−
s(v)
g(v)
=−
2µ
√
v+
4
3
νv+K
3
µ
√
v
+ν
and f (v) = [ϕ(v) + 2v]G(v). (8.160)
Substituting G(v) from (8.133) into (8.127)yields the PDE
v
t
=−2vv
xx
+ v
2
x
+
K
3
−
2
3
νv
v
x
, (8.161)
which is backward parabolic (recall that v>0 by (8.146)). We now apply transfor-
mations (i)–(v) to (8.161). The first one, (8.148), yields
w
t
=−2
1
w
2
w
x
x
+
K
3
w +
2ν
3w
x
. (8.162)
The properties of the famous quasilinear parabolic PDE,
w
t
=
1
w
2
w
x
x
,
© 2007 by Taylor & Francis Group, LLC

8 Sign-Invariants and Exact Solutions 415
have been known for a long time. In 1951, Storm [537] reduced it to the linear heat
equation by the transformation,(8.150) and (8.152).Moreover,the same can be done
for (8.162), [194] (the linear convection term K
3
w
x
is easily eliminated). See [128]
on more general approaches to linearizations of the PDEs. Let us present the corre-
sponding simple calculation for (8.162). Integrating it over (0, x) yields
∂
∂t
x
0
w(s, t)ds +
t
0
−
2w
x
w
2
+ K
3
w +
2ν
3w
(0,τ)dτ
=−
2w
x
w
2
+ K
3
w +
2
3
ν
w
.
Let z denote the function in the square brackets on the left-hand side, so that (8.150)
holds. In this case, z solves
z
t
=−
2z
xx
(z
x
)
2
+ K
3
z
x
+
2
3
ν
z
x
. (8.163)
Next, (8.152) with = (y, t)
hence, z
t
=−
t
y
reduces (8.163) to
t
=−2
yy
− K
3
−
2
3
ν(
y
)
2
.
It follows from (8.153) that V (y, t) =
y
(y, t) solves Burgers’ equation
V
t
=−2V
yy
−
4
3
νVV
y
. (8.164)
One can easily check that transformation (8.155) with coefficient (8.156) reduces
(8.164) to the heat equation
ρ
t
=−2ρ
yy
+ N
0
(t)ρ, (8.165)
with a function N
0
(t) to be determined via the consistency condition with (8.157).
Substituting the general solution (8.159) into (8.165) gives a linear DS for the
coefficient H
2
(t) and H
3
(t).
Example 8.35 Let α =−
6
ν
, β = 2andµ =−1 in (8.147). The characteristic
equation (8.158) has the form (λ −1)(λ
2
+1) = 0, which yields the general solution
ρ(y, t) = e
y
+ H
2
(t) cos y + H
3
(t) sin y. (8.166)
Plugging (8.166) into (8.165) implies N
0
(t) ≡ 2 and gives the linear DS
H
2
= 4H
2
,
H
3
= 4H
3
.
Therefore, from (8.155), we obtain the explicit solution of both (8.154) and (8.164)
V (y, t) =
3
ν
e
y
+e
4t
(−A sin y+B cos y)
e
y
+e
4t
(A cos y+B sin y)
,
where A and B are arbitrary constants, to be transformed by (iv)–(i) into the solution
of the corresponding PDE (8.127).
Example 8.36 Set now α = 0, β = 8, and µ =−5 in (8.147). In this case, from
(8.159),
ρ(y, t) = 1 + H
2
e
y
+ H
3
e
4y
,
and substituting into (8.165) yields N
0
= 0 and the solution
V (y, t) =
3
ν
Ae
y−2t
+4Be
4y−32t
1+Ae
y−2t
+Be
4y−32t
.
© 2007 by Taylor & Francis Group, LLC
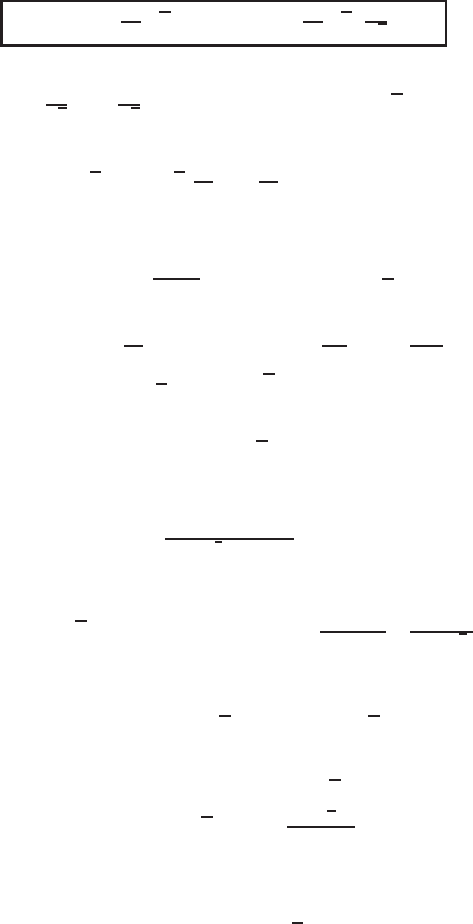
416 Exact Solutions and Invariant Subspaces
8.5.3 The linear critical case
Let ν = 0. Then the final transformation (8.155) with the coefficient (8.156) does
not make sense, and, as a result, the exact solutions are not of the exponential-
trigonometric soliton-type structure. Recall that (8.145)–(8.147) and (8.160) imply
SIs and exact solutions of the following quasilinear heat equation:
v
t
=−
2v +
K
3
µ
√
v
v
xx
+ (v
x
)
2
−
K
3
µ
√
v
α
√
v
+ β
. (8.167)
For ν = 0, integrating the stationary ODE yields
v
xx
+
µ
√
v
v
x
+
α
√
v
+ β = 0 ⇒ v
x
= (α +β
√
v)Y (v), (8.168)
with Y (v) to be determined. We then obtain the first-order ODE
√
v(α + β
√
v)
dY
dv
=−
1
2Y
(βY
2
+ 2µY + 2). (8.169)
There exist two cases:
(i) β = 0. Let
q
2
=
2β−µ
2
β
2
> 0, and set p =
µ
β
.
Integrating the ODE (8.169) yields
R(Y ) ≡
1
2β
ln[(Y + p)
2
+ q
2
] −
µ
qβ
2
tan
−1
Y +p
q
=−
1
β
ln(α +β
√
v) + E ≡ η(v),
where E = E(t) is the constant of integration. It then follows from (8.168) that
v
x
= (α +β
√
v)R
−1
(η(v)), (8.170)
and hence, solutions v = v(x , t) of (8.167) are given by the quadrature
v(x ,t)
0
dz
(α+β
√
z)R
−1
(η(z))
= x + H (t), (8.171)
with H = H (t) being yet a free function. Differentiating (8.171) in t yields
v
t
= (α + β
√
v)R
−1
(η)
H
(t) − E
(t)
v
0
1
R
−1
(η(z))
η
dz
(α+β
√
z)
. (8.172)
Plugging the derivatives(8.170) and (8.172)into the correspondingHamilton–Jacobi
PDE
v
t
= (v
x
)
2
+ (2µ
√
v + K
3
)v
x
+ 2α
√
v + 2βv,
yields the identity
H
(t) − E
(t)
v
0
(·) = (α + β
√
v)R
−1
(η(v))
+2µ
√
v + K
3
+
2
√
v
R
−1
(η(v))
,
(8.173)
where the integralon the left-hand side is the same as in (8.172). This identity should
hold for all t ∈ IR and v>0. Setting v = 0 in (8.173) yields the first ODE
H
(t) = α R
−1
E(t) −
1
β
lnα
+ K
3
. (8.174)
© 2007 by Taylor & Francis Group, LLC

8 Sign-Invariants and Exact Solutions 417
Without loss of generality, we are assuming that α>0. Otherwise, if α= 0, we
integrate in (8.171) from the limit 1. Differentiating (8.173) with respect to v, one
can check that this gives the identity if E
(t)= 1, which is the second ODE.
(ii)β= 0. This case is easier. Integrating (8.169) yields
v
x
=αR
−1
(η(v)),η(v)=−
1
α
√
v+ E(t), where
R(Y)=
1
2µ
Y−
1
µ
ln(µY+ 1)
and Y(v)=
1
α
v
x
.
Therefore, instead of (8.171), we obtain solutions of (8.167) in the form of
v(x,t)
0
dz
R
−1
(η(z))
= αx + H (t). (8.175)
In a similar fashion, the following DS is derived (cf. (8.174)):
H
(t) = α
2
R
−1
(E(t)) + αK
3
, where E
(t) = 1. (8.176)
Theorem 8.37
Under the given hypotheses, the exact solutions
(8.171)
or
(8.175)
of the PDE
(8.167)
are governed by the ODE
(8.174)
or
(8.176)
with
E(t) = t.
8.5.4 The degenerate case
1. We now consider the simplest case of the fully degenerate quadratic polynomial
(8.90), where a = b = 0, and
P(v) = c = 0.
Then P
= P
= 0andthefirst generating ODE (8.130) yields g
= 0, which gives
us g = dv + h, d = 0. Setting h = 0 by translation gives g(v) = dv. From (8.131),
we get G
(v) =
2
3
d
2
v, and hence,
G(v) =
1
9
d
2
v
3
+ K
1
v + K
2
, (8.177)
with arbitrary constants K
1
and K
2
. It then follows from (8.132) that
m(v) = 0, s(v) =
2
3
cdv + K , and M(v) = 2cG(v), (8.178)
where K is arbitrary. Finally, from (8.129), we derive the following class of quasi-
linear heat equations:
v
t
=−
1
dv
2
3
cdv + K
v
xx
+
1
dv
4
3
cdv − K
G(v), (8.179)
which admit the SI
H[v] = v
t
−
2
3
cdv + K
v
x
− 2cG(v).
2. The construction of exact solutions of (8.179) is also easier than in the previous
case. The corresponding stationary ODE
v
xx
+ dvv
x
+
1
9
d
2
v
3
+ K
1
v + K
2
= 0 (8.180)
is linearized by the transformation
v =
3
d
ρ
x
ρ
. (8.181)
© 2007 by Taylor & Francis Group, LLC

418 Exact Solutions and Invariant Subspaces
This yields the linear-third order ODE
ρ
xxx
+ K
1
ρ
x
+
1
3
dK
2
ρ = 0, (8.182)
which results in the linear representation (8.159) of the general solution.
3. Substituting G(v) (as given in (8.177)) from (8.180) into (8.179) yields the classi-
cal Burgers equation
v
t
=−2cv
xx
−
4
3
cdv − K
v
x
,
which, by (8.181), reduces to the linear heat equation with lower-order terms
ρ
t
=−2cρ
xx
+ Kρ
x
+ N
0
(t)ρ. (8.183)
The rest of the analysis of the consistent system (8.182), (8.183) is similar.
Example 8.38 Setting K
1
=−1andK
2
= 0 in (8.182) gives the solution
ρ = 1 + H
2
e
x
+ H
3
e
−x
of the linearized stationary ODE. Substituting into (8.183) yields N
0
= 0andthe
explicit solution of (8.179),
v(x , t) =
3
d
Ae
x+(K −2c)t
−Be
−x −(K +2c)t
1+Ae
x+(K −2c)t
+Be
−x −(K +2c)t
.
Example 8.39 Now let K
1
= 0anddK
2
=−3. Then,
ρ = e
x
+ e
−
x
2
H
2
sin
√
3x
2
+ H
3
cos
√
3x
2
.
Substituting into the heat equation (8.183) implies that N
0
= 2c − K , and that the
coefficients H
2
(t) and H
3
(t) solve the linear DS
H
2
= 3
c −
K
2
H
2
−
√
3
c +
K
2
H
3
,
H
3
=
√
3
c +
1
2
H
2
+ 3
c −
1
2
H
3
,
which is easily integrated.In particular,for K =−2c,wehavethesolutionof(8.179)
v =
3
2d
2e
x
+e
6ct−
x
2
[(A
√
3−B) cos
√
3x
2
−(B
√
3+A) sin
√
3x
2
]
e
x
+e
6ct−
x
2
(A sin
√
3x
2
+B cos
√
3x
2
)
.
8.5.5 P(v) is a quadratic polynomial
Finally, we study the most interesting case a = 0, where (8.90) is a quadratic poly-
nomial.
1. Single-term polynomial. Considerfirst the case of the single-termquadraticpoly-
nomial
P(v) =
1
2
av
2
, with a = 0(i.e.,b = c = 0). (8.184)
Then the generating equations (8.130) and (8.131) are solved explicitly,
g(v) = µv
2
+
ν
v
4
and G(v) =
α
v
3
+ βv +
1
16
µ
2
v
5
−
ν
2
v
7
, (8.185)
where G
0
(v) =
α
v
3
+ βv is the general solution of (8.131).
© 2007 by Taylor & Francis Group, LLC
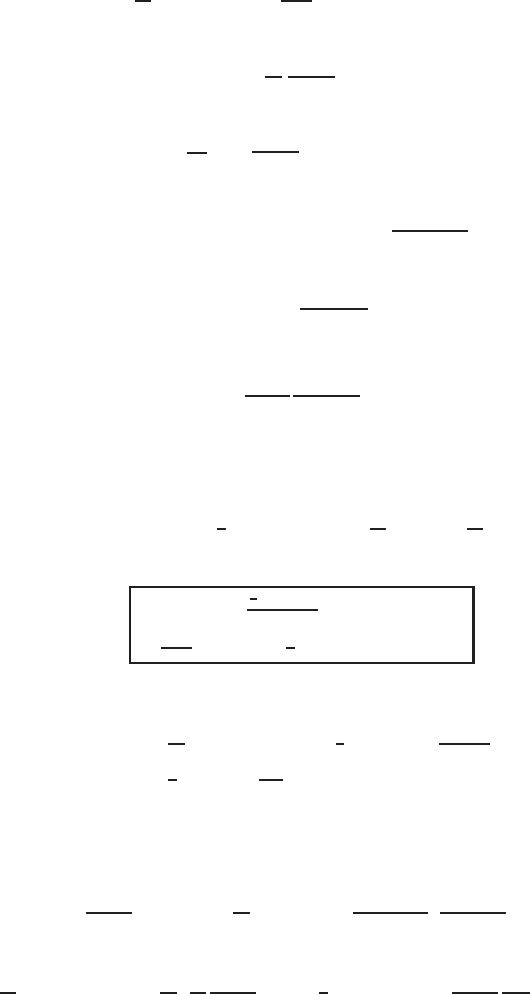
8 Sign-Invariants and Exact Solutions 419
Let us begin with the structure of exact solutions in the case where α = β = 0in
(8.185). The stationary ODE (8.133),
v
xx
+
1
v
4
(µv
6
+ ν)v
x
+
1
16v
7
(µv
6
− ν)(µv
6
+ ν) = 0,
can then be integrated in quadratures. Introducing the new function Y by
v
x
=
1
16
µv
6
−ν
v
3
Y (v), (8.186)
gives the first-order ODE
vY
dY
dv
=−
µv
6
+ν
µv
6
−ν
(Y + 4)(3Y + 4). (8.187)
Integrating yields
Y = R
−1
(η(v)), where η(v) =
v
2
(µv
6
−ν)
2/3
E, (8.188)
E is a free constant and R
−1
is the inverse function to
R(Y ) =
Y +4
(3Y +4)
1/3
. (8.189)
Integrating (8.186) with Y from (8.188) gives the following solutions v(x, t):
16
v(x ,t)
1
z
3
µz
6
−ν
dz
R
−1
(η(z))
= x + H. (8.190)
Here, E = E(t) and H = H (t) are some smooth functions to be determined by sub-
stituting (8.190) into the corresponding Hamilton–Jacobi PDE with the coefficients
calculated by (8.132),
H[v] ≡ v
t
−
av(v
x
)
2
+
1
2
aµv
4
+ K
v
x
+
a
16
µ
2
v
7
−
ν
2
v
5
= 0. (8.191)
Using (8.129), (8.184), and (8.185) yields the quasilinear heat equation
v
t
=−v
4
1
2
aµv
4
+K
µv
6
+ν
v
xx
+ av(v
x
)
2
+
1
16v
5
(µv
6
− ν)
1
2
aµv
6
+ aν − K v
2
.
(8.192)
Theorem 8.40
The parabolic PDE
(8.192)
admits the sign-invariant
(8.191)
and
solutions
(8.190)
, where the functions
E(t)
in
(8.188)
and
H (t)
satisfy the DS
H
=
1
16
a(µ − ν)g
E
(t) +
1
2
aµ + K +
a(µ+ν)
g
E
(t)
,
E
=
1
2
aµν E +
1
128
aE
4
,
(8.193)
where
g
E
(t) = R
−1
(E(t)(µ − ν)
−2/3
).
Proof. We follow the same lines, as in the linear critical case. Calculating derivative
v
t
from (8.190),
v
t
=
µv
6
−ν
v
3
R
−1
(η(v))
1
16
H
− E
v
1
z
5
(µz
6
−ν)
5/3
1
R
−1
(η(z))
η
dz
,
and substituting into (8.191), together with v
x
from (8.186), we derive the identity
1
16
H
− E
v
1
(·) =
1
16
a
16
µv
6
−ν
v
2
R
−1
+
1
2
aµv
4
+ K + a
µv
6
+ν
v
2
1
R
−1
. (8.194)
© 2007 by Taylor & Francis Group, LLC

420 Exact Solutions and Invariant Subspaces
Here, settingv= 1 yields the first ODE (8.193). Differentiating (8.194) with respect
tov and using (8.188) implies the following ODE:
vY
dY
dv
=−
2(2µv
6
+ν)Y
2
Y+
4(2µv
6
−
ν)
2µv
6
+ν
(Y+4)
(µv
6
−ν)Y
2
−
256γv
6
µv
6
+ν
+16(µv
6
+ν)
, with γ=−
E
2aE
. (8.195)
Let us compare ODEs (8.195) and (8.187), which must admit a common solution
given by (8.188) and (8.189). The right-hand sides of both equations (8.195) and
(8.187) coincide if Y= Y(v) solves the cubic algebraic equation
Y
3
+ 12Y
2
+
16+
64v
6
(4γ+µν)
(µv
6
−ν)
2
(3Y+ 4)= 0. (8.196)
On the other hand, expressions (8.188) and (8.189) can be written in the form of the
following cubic equation:
Y
3
+ 12Y
2
+
16−
E
3
v
6
(µv
6
−ν)
2
(3Y+ 4)= 0. (8.197)
The last coefficients of the term(3Y+ 4) of (8.196) and (8.197) coincide if 256γ=
−64µν− E
3
, from which comes the second ODE in (8.193).
2. A solution for general polynomial. Consider another solution of the generating
ODEs. We again assume that a= 0, and, by translation, take the quadratic polyno-
mial in the most general form
P(v)=
1
2
(av
2
+ 2c), (8.198)
where c= 0. Then the system (8.130), (8.131) has the general solution
g(v)=
1
4
(2av
2
+ c) and
G(v)=
1
64
(a
2
v
5
+ 2acv
3
)+αG
0
(v)+βv,
whereα andβ are arbitrary constants, and G
0
(v) denotes the second solution of the
homogeneous equation (8.131) such that G
0
(v) and v are linearly independent.
Let us restrict ourselves to the quadrature case
α = 0andβ =
3
256
c
2
.
Then, setting in the corresponding stationary equation (cf. (8.186))
v
x
=
1
192
(2av
3
+ 3cv)Y (v) (8.199)
yields the ODE
Y
dY
dv
=−
6av
2
+3c
2av
3
+3cv
(Y + 4)(Y + 12), so (8.200)
Y = R
−1
(η(v)), η(v) =
E
144
(2av
3
+ 3cv)
2
, R(Y ) =
Y +4
(Y +12)
3
. (8.201)
Integrating (8.199) yields the following solutions:
192
v(x ,t)
1
1
2az
3
+3cz
dz
R
−1
(η(z))
= x + H. (8.202)
The Hamilton–Jacobi PDE is now
H[v] ≡ v
t
−
av(v
x
)
2
+
1
4
(a
2
v
4
+ 2acv
2
+ K )v
x
+
1
256
(av
2
+ 2c)(4a
2
v
5
+ 8acv
3
+ 3c
2
v)
= 0.
(8.203)
© 2007 by Taylor & Francis Group, LLC
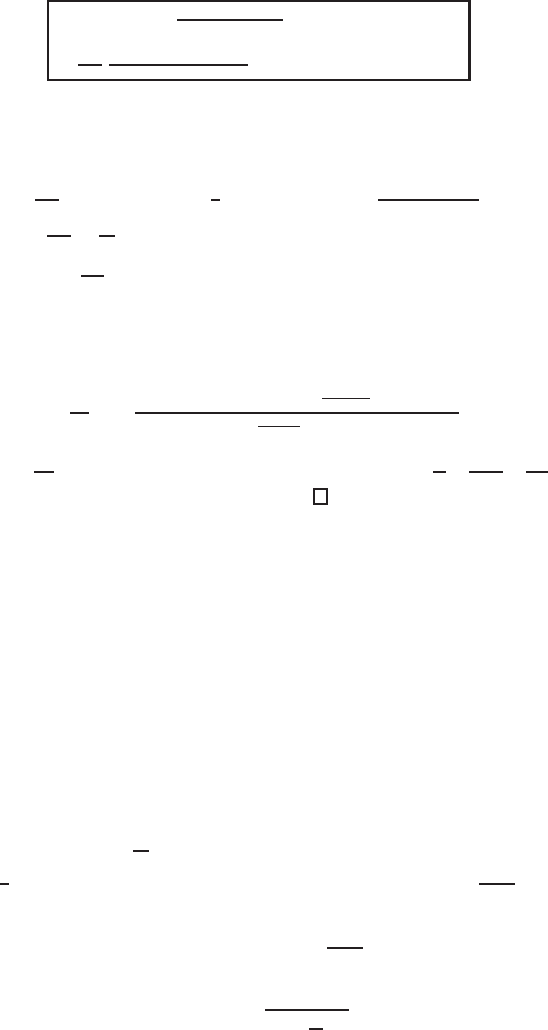
8 Sign-Invariants and Exact Solutions 421
The quasilinear heat equation takes the following (rather awkward) form:
v
t
=−
a
2
v
4
+2acv
2
+K
2av
2
+c
v
xx
+ av(v
x
)
2
+
1
256
a
2
v
4
+3acv
2
+2c
2
−K
2av
2
+c
(4a
2
v
5
+ 8acv
3
+ 3c
2
v),
(8.204)
where a, c,andK are arbitrary constants.
Theorem 8.41
PDE
(8.204)
admits the sign-invariant
(8.203)
and solutions
(8.202)
,
where the coefficients
E(t)
in
(8.201)
and
H (t)
satisfy the DS
H
=
a
192
(2a + 3c)g
E
(t) +
1
4
(a
2
+ 2ac + K ) +
3(a+2c)(2a+c)
4g
E
(t)
,
E
=−
a
128
−
3
64
c
3
E,
(8.205)
with
g
E
(t) = R
−1
(
1
144
E(t)(2a + 3c)
2
)
.
Proof. Calculating v
t
from (8.202), and substituting both derivatives v
x
and v
t
into
(8.203) (where setting v = 1 in the identity gives the first ODE (8.205)), after differ-
entiating in v, we obtain
Y
dY
dv
=−
2av(4av
2
+3c)Y
2
Y +12
4av
2
+5c
4av
2
+3c
(Y +12)
av
2
(2av
2
+3c)Y
2
+
12288γ
2av
2
+c
−144(av
2
+2c)(2av
2
+c)
,
where γ =−
E
2E
. It admits solution (8.201) satisfying (8.200) if
1
E
−
256γ
a
+
6c
3
a
= 0,
from which comes the second ODE in (8.205).
Due to Theorem 8.32, the DS (8.135) is always given explicitly in all the cases
(as well as in other cases of sets described by the stationary equation (8.133)).In the
case of (8.198), the corresponding solutions v(x, t), in general, do not have explicit
quadrature representation, excluding the cases considered.
8.5.6 Interpretation via invariant subspaces and sets
It is not often easy to interpret some of the obtained solutions by using the current
ideology of linear subspaces that are (partially) invariant under nonlinear operators.
As usual, such interpretations help to reconstruct extensions to higher-order PDEs,
avoiding technical manipulations.
Example 8.42 (Semilinear equation) Consider the simplest quasilinear case. Fix
a = 1 in (8.184) and set µ = ν = 0 in (8.185) ( i.e., g(v) ≡ 0) and α = 1,β= 0
in (8.185) (i.e., G(v) =
1
v
3
). Next, from (8.132), take m(v) = v, s(v) = 0, and
M(v) =
1
v
,andfinally find from (8.129) that ϕ(v) = 1and f (v) =
1+v
2
v
3
.Wethen
obtain the following semilinear heat equation:
v
t
= v
xx
+ v(v
x
)
2
+
1+v
2
v
3
(8.206)
that possesses the explicit solution of the typical self-similar form
v
∗
(x , t) =
2t −
1
2t
x
2
. (8.207)
© 2007 by Taylor & Francis Group, LLC

422 Exact Solutions and Invariant Subspaces
But (8.207) is not self-similar, in the sense that it cannot be constructedby symmetry
group analysis. In view of (8.207), we introduce V = v
2
, so that
V
t
= F
1
[V ] + F
2
[V ] ≡
V
xx
−
1
2V
(V
x
)
2
+
2
V
+
1
2
(V
x
)
2
+ 2
. (8.208)
The corresponding explicit solution is
V
∗
(x , t) ≡ (v
∗
)
2
= 2t −
1
2t
x
2
∈ W
2
= L{1, x
2
}, (8.209)
for all t > 0, where the 2D subspace W
2
is invariant under the second Hamilton–
Jacobi operator F
2
in (8.208), but not under the operator F
1
. Indeed, we have, for
V = C
1
+ C
2
x
2
∈ W
2
,
F
2
[V ] = 2 +2C
2
2
x
2
∈ W
2
and F
1
[V ] =
2(C
1
C
2
+1)
C
1
+C
2
x
2
.
We next introduce the following set on W
2
:
M =
V = C
1
+ C
2
x
2
: F
1
[V ] = 0, i.e., C
1
C
2
+ 1 = 0
,
which is invariant on W
2
under the full operator F
1
+ F
2
in (8.208). Substituting
V (x, t) = C
1
(t) + C
2
(t)x
2
, implies that (8.208) on M is the overdetermined DS,
which gives (8.209),
C
1
= 2,
C
2
= 2C
2
2
,
C
1
C
2
+ 1 = 0.
Example 8.43 (Higher-order PDEs)Asthefirst obvious extension, note that the
explicit solution (8.209) satisfies any of the PDEs of arbitrary order
V
t
= ψ(V , V
x
, V
xx
, ...)F
1
[V ] + F
2
[V ], (8.210)
with an arbitrary function ψ(·). For a more subtle example, consider the following
fourth-order parabolic PDE:
V
t
=
−V
xxxx
+
1
6V
(V
xx
)
2
−
24
V
+
1
6
(V
xx
)
2
+ 24
. (8.211)
Then, introducing a similar set, M ⊂ W
2
, and looking for solutions V
∗
(x , t) =
C
1
(t) + C
2
(t)x
4
on W
2
= L{1, x
4
} yields the consistent overdeterminedDS,
C
1
= 24,
C
2
= 24C
2
2
,
C
1
C
2
+ 1 = 0,
i.e., C
1
(t) = 24t and C
2
(t) =−
1
24t
, from which comes the solution of (8.211),
V
∗
(x , t) = 24t −
1
24t
x
4
.
Example 8.44 (Semilinear heat equation) Setting again a = 1andµ = ν = 0,
we now take α = β = 1, i.e., according to (8.185), G(v) = v +
1
v
3
. Then v and
V = v
2
solve the equations
v
t
= v
xx
+ v(v
x
)
2
+ (1 + v
2
)
v +
1
v
3
⇒
© 2007 by Taylor & Francis Group, LLC
