Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics

Подождите немного. Документ загружается.

7 Partially Invariant Subspaces and GSV 383

in the separation problem (7.190) will lead to g(x , t) containing extra linear terms

g(x, t) = b(t)



i=1

− ψ

(t))



i=K +1

(t)x

+ A(t). (7.210)

The principal calculations for deriving the corresponding ODE system (7.201), the

results, and formulae remain the same, with N replaced by K . Moreover, the ODEs

for extra coefﬁcients C

immediately imply that C

= 0foralli ≥ K +1. Therefore,

explicit solutions with functions (7.209) and (7.210) truly belong to IR

and this

representation cannot supply us with new solutions.

Remarks and comments on the literature

The current notion of invariant sets on linear subspaces W

(partial invariance) was introduced

in [239], where various applications to PDEs with quadratic and cubic operators can be found

(wehavereﬂected some of the applications in this chapter).

§7.1.Solutions (7.4) were obtained in [397], where the solution structure (7.25) was also

proposed for a nonlinear second-order parabolic PDE.

§7.2.Quasilinear KS-type models were considered in [570], where some usual compactons

(7.37) with p = 0, were constructed.

§7.3.We use a slightly different version of the GSV introduced in [238], some other results

are taken from [239]. By the transformation

v = c

equation (7.86) reduces to a PDE with cubic nonlinearities, to which Baker–Hirota transfor-

mations apply, [100, 329]. Solutions (7.87) of equation (7.86) were also obtained by another

approach based on evolutionary invariant sets, [317].

§7.5.We mainly follow [225]. Notice that the orbits of ODEs (7.143) satisfy the comparison

principle, so that, for all the PDEs under consideration, the ﬂows on sets M

are ordered

with respect to initial data. This is a natural property for the second-order parabolic equations

(in view of the Maximum Principle), but is rather surprising for higher-order PDEs, though

possibly it just reﬂects a simple geometric structure of these sets. The solution structure (7.139)

corresponds to the functional separation of variables; see Remarks to Section 8.4 for history

and references.

Further applications of evolutionary invariant sets to TFEs were given in [478], where the

extension of (7.132) in the form of the Bernoulli ODE

u + u

was used (note that almost all explicit solutions therein admit polynomial representation on

partially invariant subspaces); see also [479] for further extensions concerning sets (7.147).

There exist attempts to treat general sets

= G(x, t, u)

which often lead to complicated calculus; see [440] and Section 8.3 for parabolic equations.

Applications to the KdV-type equations

= u

xxx

+ ψ(u)u

(7.211)

and to more general quasilinear ones, can be found in [223]. For (7.211), the ODE for H is

H(HH



)



− 6HH



− 3(H



)

+ 9H



− 6 = 0, where ψ(u) = exp





H(z)



. (7.212)

384 Exact Solutions and Invariant Subspaces

It is curious that (7.212) admits two linear solutions, (i) H

(u) = u, i.e., the KdV equation,

= u

xxx

+ uu

, and (ii) H

(u) = 2u, corresponding to

= u

xxx

√

possessing the explicit blow-up solution

u(x, t) =

(−t)

Therefore, the KdV equation plays the role of a “limit” one (for u  1) in the family of PDEs

(7.211) admitting M

; see details in [223]. Let us point out another KdV-type equation

= u

xxx

+ lnuu

that admits explicit solutions

u(x, t ) = e

(t)+C

(t)x

on a simple linear subspace with





= C

+ C



= C

§7.6.Exact solutions (7.197) in IR

and IR

were constructed in [57] by the direct similarity

reduction (in IR

)

u(x, t) = ar f (θ), where (7.213)



= x

+ (x

− Vt)

θ = tan

−1

−Vt

The resulting ODE for f admits the explicit solution

f (θ) =

(1 −cos θ).

Similar solutions were constructed [58] for the fourth-order TFE

=−∇·(u

∇u) in IR

× IR

, (7.214)

but, in this case, the ODE for f in (7.213) cannot be solved explicitly for n = 3. This con-

ﬁrms the general conclusion that the solution structure (7.184) does not apply to higher-order

PDEs. Substituting this into (7.214) with n = 1(orn = 2) leads to the analysis on linear

subspaces of dimension larger than two that makes the PDE system more overdetermined and

the consistency much more suspicious.

The form of solutions (7.184), (7.186) was proposed by the authors of [501] (see earlier

references therein), where systems (7.187) and that for p =

were derived and partially ana-

lyzed (our more complete analysis is different). Exact solutions with the quadratic g(x, t) for

N = 2, m = 0 can be found in [502] (other solutions in IR

constructed therein for which

functions f and g are quadratic on 2D subspaces only, represent the same case). Some solu-

tions in the case of (7.208) were detected in [501] by a sophisticated computational approach;

as we have shown, other solutions there with quadratic forms in IR

for all dimensions K < N

are of the same nature and are not new.

Open problems

• In particular, some open problems are given in Sections 7.2, 7.4.4, 7.4.5, and

7.5.1.

CHAPTER 8

Sign-Invariants for Second-Order Parabolic

Equations and Exact Solutions

We underline a new important aspect of invariant subspaces for nonlinear operators. Our goal

is to show that, for second-order parabolic PDEs, proper families of exact solutions may deﬁne

the so-called sign-invariants (SIs) of parabolic ﬂows, which are nonlinear operators preserving

their signs, “

≥

” and “

≤

,” on evolution orbits. Vice versa, the known SIs may specify the cor-

responding exact solutions. We will mainly concentrate on the related backward problem: by

constructing sign-invariants describe subspaces or sets of the corresponding solutions. Many

SIs are generated by differential constraints, which thus preserve their signs. This is an impor-

tant (and not always well understood) feature of differential constraints for parabolic equations

obeying the Maximum Principle.

Our basic model is a quasilinear heat equation of the general form

= F[u] ≡∇·(k(u)∇u) + f (u) in IR

× IR

, (8.1)

where k(u) ≥ 0and f (u) are given smooth functions. We will consider the Cauchy

problem for (8.1) with given sufﬁciently smooth initial data u(x, 0) = u

(x ) in IR

and assume that there exists a unique sufﬁciently smooth solution u = u(x , t),at

least locally in time.

We say that the ﬁrst-order operator H[u] = H (x , u, ∇u, u

) is a sign-invariant

(SI) of the equation (8.1) if, for any solution u(x , t), the following holds:

(1) H[u(x, 0)] ≥ 0inIR

⇒ H[u(x, t)] ≥ 0inIR

for t > 0,

(2) H[u(x, 0)] ≤ 0inIR

⇒ H[u(x, t)] ≤ 0inIR

for t > 0,

i.e., both signs of H[u] are preserved in evolution. Such an evolution invariance of

signs is controlled by the Maximum Principle (MP). Since, by deﬁnition, any sign-

invariant H[u]isalsothezero-invariant, i.e.,

H[u(x, 0)] = 0inIR

⇒ H[u(x, t)] = 0inIR

for t > 0, (8.2)

this makes it possible to construct exact solutions of equations (8.1) if we know how

to integrate the ﬁrst-order PDE in (8.2). We will derive ﬁnite and, in some cases,

inﬁnite-dimensional sets of equations (8.1) possessing solutions that are expressed

in terms of dynamical systems or algebraic relations. It turns out that these solutions

often belong to some linear invariant subspaces or sets.

Using these connections with SIs, a number of higher-order PDEs admitting sim-

ilar subspaces and solutions will be found. In view of the lack of the MP, we then

lose the SI properties, but the rest of the analysis, including exact solutions, remains

valid.

386 Exact Solutions and Invariant Subspaces

8.1 Quasilinear models, deﬁnitions, and ﬁrst examples

Thus, in order to avoid posing suitable boundary conditions, which are not essential

in the present context, we consider the Cauchy problem with smooth initial data

u(x , 0) = u

(x ) in IR

, (8.3)

and assume that there exists a unique local-in-time solution u(x, t). According to

classical parabolic theory, this requires some extra hypotheses on the coefﬁcients of

(8.1) and on the class of initial functions u

8.1.1 On weak and proper solutions

We illustrate our main results by taking quasilinear heat equations (8.1), which are

widely used in applications in diffusion, combustion, and ﬁltration theory. Since we

are going to use the MP, let us be more speciﬁc about the nonlinear coefﬁcients

of the PDEs under consideration. The functions k(u) and f (u) are assumed to be

sufﬁciently smooth. For solvability of parabolic PDEs, we impose the parabolicity

condition

k(u) ≥ 0.

For k(u) ≡ 1, there occurs the semilinear heat equation

= F

[u] ≡ u + f (u) in IR

× IR

, (8.4)

where  is the Laplace operator in IR

. For smooth functions f (u), the Cauchy

problem for such equations admits a unique classical solution. Even for uniformly

parabolic equations, for non-Lipschitz or singular absorption terms, such as

f (u) =−u

, with the exponent p ∈ (−1, 1) (8.5)

(we have dealt with modelslike that before, especially for f (u) =−1forp = 0),the

nonnegative solutions may exhibit ﬁnite interfaces and need smooth approximations

as weak or maximal/minimal proper solutions. Furthermore, we do not hesitate to

consider degenerate PDEs (8.1) with k(0) = 0, e.g., the PME, where k(u) = u

with a ﬁxed exponent σ>0. For the PME, weak solutions u(x , t) of the Cauchy

problem can be compactly supported and are not smooth at the interfaces, where

u= 0, and the PDE is degenerate. See basics of PME theory in [245, Ch. 2]. In this

case, to justify manipulations with derivatives, we impose a conventionalassumption

that we actually deal with regular approximations of weak solutions. We assume that

the weak solution u(x , t) is determined as the limit of a sequence {u

} of smooth

solutions,

u(x , t) = lim u

(x , t) as n →∞.

Here, each solution u

(x , t) solves a regularizeduniformly parabolic PDE (8.1)with

the heat conduction coefﬁcient k(u) replaced by its strictly positive approximation

(u) satisfying k

(u) ≥

> 0forallu,andk

→ k as n →∞uniformly on

bounded u-intervals. For instance,

(u) =



(u) +

8 Sign-Invariants and Exact Solutions 387

For non-smooth absorption terms (8.5), the uniformly Lipschitz (analytic) approxi-

mation

(u) =



+ u



p−1

is also used. If necessary, initial data are replaced by bounded smoother truncations

(x ) → u

(x ) as n →∞uniformly on compact subsets.

The PDE for u

(x , t) is uniformly parabolic with smooth coefﬁcients, so u

(x , t)

is regular enough for our manipulations. The approximation (regularization) tech-

niques lie in the heart of modern theory of quasilinear singular parabolic PDEs of

arbitrary order; see references in [226, Sect. 6.2]

8.1.2 Maximum Principle and ﬁrst examples of sign-invariants

The MP is the cornerstone of classical theory of second order parabolic PDEs, as ex-

plained in many well-known books and monographs, [148, 164, 205, 472, 530]. The

MP and various order-preserving comparison techniques and results are associated

with the fact that the Laplacian u has deﬁnite signs “≥” or “≤” at an extremum in

x for C

smooth solutions u(x, t). For instance, as a typical simple application of the

MP for equations (8.1) and (8.4) with smooth coefﬁcients and f (0) = 0, we have

the comparison with the trivial solutions u = 0, i.e.,

(x ) ≥ 0 (≤ 0) in IR

⇒ u(x, t) ≥ 0 (≤ 0) in IR

for t > 0. (8.6)

This is the evolution invariance of the sign of the solutions u(x , t). On the other

hand, a slightly modiﬁed comparison implies that the monotonicity with time prop-

erty holds

(x , 0) ≥ 0 (≤ 0) in IR

⇒ u

(x , t) ≥ 0 (≤ 0) in IR

for t > 0. (8.7)

This is the invariance with time of the sign of the derivativeu

(in fact, this represents

a ﬁrst simpleSI). Bearingin mind necessaryhypotheseson the coefﬁcientsand initial

data, here the MP in the following form is used. Let a smoothfunction J (x , t) satisfy

a linear parabolic PDE

= M[J ] ≡ A J +B ·∇J +CJ in IR

× IR

, (8.8)

where A ≥ 0, B = (B

, ..., B

),andC are given bounded coefﬁcients, depending

on x, t, and possibly u (the dot “·” denotes the scalar product in IR

). Then,

J (x, 0) ≥ 0 (≤ 0) in IR

⇒ J (x, t) ≥ 0 (≤ 0) in IR

for t > 0.

As above, a rigorous proof uses suitable hypotheses on the coefﬁcients of (8.8) and

also on the behavior of J(x, t) as |x |→∞.

Therefore, property (8.6) follows immediately from the MP, since equations (8.1)

and (8.4) have been already written down in the form of (8.8) for the function J = u.

To show (8.7), one needs to differentiate the PDE with respect to t to obtain (8.8) for

J = u

, assuming, as usual, that the regularity of all the functions and coefﬁcients is

enough for such manipulations.For instance, differentiating (8.1) yields, for J = u

= k(u)J + 2∇k(u) ·∇J +[k(u) + f



(u)]J, (8.9)

388 Exact Solutions and Invariant Subspaces

which is precisely (8.8) with A = k(u), B = 2∇k(u),andC = k(u) + f



(u).

In addition,since the ﬁrst x

-derivative J = u

for anyi = 1, 2, ..., N satisﬁes the

same equation (8.9), the MP also implies the following space monotonicity property

(cf. (8.7)):

)

≥ 0 (≤ 0) in IR

⇒ u

(x , t) ≥ 0 (≤ 0) in IR

for t > 0.

This means the evolution invariance of the sign of u

. We next consider examples

of more complicated and practical SIs.

8.1.3 First-order sign-invariants

We turn to the general problem of ﬁnding ﬁrst-order SIs for a general fully nonlinear

parabolic PDE of the form

P[u] ≡ u

− L(x, u, ∇u,u) = 0inIR

× IR

, (8.10)

where L(x, u, p, q) is a given C

∞

-function satisfying the parabolicity condition



(x , u, p, q) ≥ 0inIR

× IR × IR

× IR . (8.11)

As above, consider the Cauchy problem for (8.10) with initial data (8.3). For conve-

nience, let us introduce the set of proper initial functions and solutions of (8.10),

={u

(x ) ∈ C

: ∃ a unique solution u(x , t) ∈ C

∞



={u ∈ C

: u(x , t) solves (8.10) with u

∈ ω

Consider a general nonlinear ﬁrst-order Hamilton–Jacobi operator of the form

H[u] ≡ H (x, u, ∇u, u

), (8.12)

where H (x, u, p, q) is a C

∞

-function. We will study the sign of H[u] on the evolu-

tion orbits from 

. Therefore, consider the reduced operator

[u] ≡ H (x, u, ∇u, L(x , u, ∇u,u)) in 

where u

is replaced by L(x, u, ∇u,u) via (8.10). This gives the following sets:

H,P



v(x ) ∈ C

: H

[v] ≥ 0inIR



∩ ω

, (8.13)

−

H,P



v(x ) ∈ C

: H

[v] ≤ 0inIR



∩ ω

. (8.14)

Deﬁnition 8.1 The ﬁrst-order operator (8.12) is said to be a sign-invariant of the

equation (8.10) if both signs of H are preserved with time,

∀u

∈ S

H,P

−

H,P

) ⇒ u(·, t) ∈ S

H,P

−

H,P

) for t > 0. (8.15)

If the sign of the operator (8.12) on evolution orbits {u(x , t), t > 0}, i.e., the

inequality

[u(x , t)] ≥ 0 (or ≤ 0) in IR

for t > 0,

is known, integrating it yields estimates for solutions of the nonlinear parabolic PDE

(8.10). Very often such estimates are an important part of general parabolic theory,

8 Sign-Invariants and Exact Solutions 389

where the structural properties of possible operators H[u] play a key role. In sub-

sequent sections, we present special approaches to ﬁnding nontrivial pairs of the

operators {P , H} such that (8.15) holds.

8.1.4 Sign-invariants, zero-invariants, exact solution, and differential constraints

Using (8.13) and (8.14), it is natural to introduce the set

H,P

= S

H,P

∩ S

−

H,P



v(x ) ∈ C

∞

: H

[v] = 0inIR



∩ ω

It follows from (8.15) that any SI (8.12) also becomes a zero-invariant of (8.10),

in the sense that the set S

H,P

is evolutionary invariant under the ﬂow generated by

(8.10), i.e.,

∀u

∈ S

H,P

⇒ u(·, t) ∈ S

H,P

for t > 0.

This implies that the parabolic equation (8.10) restricted to the invariant set S

H,P

equivalent to the Hamilton–Jacobi equation

H (x, u, ∇u, u

) = 0, with u(·, t) ∈ S

H,P

for t > 0. (8.16)

It is easier to solve the ﬁrst-order equation (8.16) than the second-order parabolic

PDE (8.10), and, in some cases, this can be done explicitly. In several cases, such

exact solutions can be treated from the point of view of linear ﬁnite-dimensional

subspaces that are (partially) invariant under certain nonlinear operators.

In terms of zero-invariants, (8.16) represents a differential constraint associated

with the nonlinear PDE (8.10). In general, the problem of determining differential

constraints (in our case, the function H (·)) is reduced to a complicated nonlinear

PDE for H (a compatibility condition), depending on the operator L. This problem

cannot be solved even in simpler particular cases. We ﬁnd several examples, show-

ing how to ﬁnd a ﬁrst-order differential constraint. In this analysis, we use some

known approaches via the MP coming from qualitative theory of nonlinear parabolic

PDEs. In particular, we essentially use results from the theory of blow-up solutions

of quasilinear heat equations, which was the origin of a number of new ideas and

techniques.

8.2 Sign-invariants of the form u

− ψ(u)

Let us apply such SIs to general fully nonlinear parabolic PDEs

P[u] ≡ u

− L(u, |∇u|,u) = 0inIR

× IR

, (8.17)

where L(u, p, q) issmoothand satisﬁes the parabolicityconditionlike (8.11).There-

fore, we may assume that there exists a smooth function +

(u, p, s) such that

L(u, p,+

(u, p, s)) ≡ s for (u, p, s) ∈ IR × IR

× IR . (8.18)

We will look for SIs of (8.17) of the form

H[u] ≡ u

− ψ(u), (8.19)

390 Exact Solutions and Invariant Subspaces

where ψ(u) is a smooth unknown function. Set

−1

(u, p) = +

(u, p,ψ(u)), (8.20)

and denote L

(u, p, q) =

∂ L

∂u

and L

(u, p, q) =

∂ L

∂p

, ..., where the argument q is

replaced by +

(u, p,ψ(u)).

Theorem 8.1

Operator

(8.19)

is a sign-invariantof the equation

(8.17)

satisﬁes

the following identity for

(u, p) ∈ IR × IR

F(u, p) = (L

− ψ



)ψ + L



p + L

(ψ



+ ψ



−1

) ≡ 0. (8.21)

Proof. Setting J = u

− ψ(u) yields, on differentiation,

= u

− ψ



. (8.22)

Calculating u

from (8.17) implies

= L

+ L

(∇u ·∇u

)

|∇u|

+ L

u

. (8.23)

Since u

= J + ψ(u), J solves a linear parabolic PDE of the form

= M[J ] +F, (8.24)

where M is an elliptic operator as in (8.8) with A = L

and coefﬁcients B and C

from (8.23). By the MP, it follows from (8.24) that (8.19) is an SI if (8.21) holds.

Assuming a one-sided partial differential inequality for F,say,

F(u, p) = (L

− ψ



)ψ + L



p + L

(ψ



+ ψ



−1

) ≥ 0, (8.25)

the MP guarantees that precisely the sign “≥” is only preserved for the operator

(8.19), i.e.,

− ψ(u) ≥ 0fort > 0inIR

, (8.26)

provided that the same inequality holds for the initial data at t = 0. In classical

parabolic theory, such one-sided inequalities are typically associated with the bar-

rier techniques. Of course, if only a one-sided estimate is necessary, this essentially

widens the set of possible solutions {ψ} of the partial differential inequality (PDI)

(8.25) and gives other estimates by integrating the PDI (8.26). The one-sided ap-

proach is not associated with exact solutions, and will not be considered in this

text. One-sided estimates have a range of important applications in blow-up theory

of reaction-diffusion PDEs; different applications are described in [509, Ch. 7] and

[245, Ch. 10].

Let us return to the main identity (8.21) that is a nonlinear PDE for ψ,whichis

difﬁcult to analyze for general operators L in (8.17). Our study is now restricted to

the class of quasilinear heat equations.

8.2.1 Quasilinear heat equations and higher-order extensions

As the ﬁrst application of Theorem 8.1, consider quasilinear equations (8.1) for

which (8.21) reduces to a system of two ODEs.

8 Sign-invariants and Exact Solutions 391

Corollary 8.2 Operator (8.19) is a sign-invariant of equation (8.1) iff ψ(u) satisﬁes

the ODE system



(kψ)



= 0, k



− f



kψ





= 0. (8.27)

Proof. By (8.1), L(u, p, q) = kq + k



+ f, so that

−1

(ψ − f − k



), L

= 2k



p, L

= k,

and L





−



)



+ f



(ψ − f ).

(8.28)

Plugging (8.28) into (8.21) yields

F(u, p) = k



(kψ)







− f



kψ





Since the variables u and p are independent, identity (8.21) is valid, provided that

(8.27) holds.

The system of ODEs (8.27) for two unknowns {ψ, f } can be easily integrated.

This yields the following family of equations.

Example 8.3 (Invariant subspaces: blow-up)Letϕ(u) be an arbitrary smooth

function such that the inverse ϕ

−1

exists. Denote k(u) = ϕ



(u) ≥ 0. Solving (8.27)

gives the quasilinear heat equation

= ϕ(u) +

aϕ(u)+b



(u)

+ [aϕ(u) + b]c, (8.29)

where a

+ b

= 0. By (8.19), the PDE (8.29) admits the following SI:

H[u] ≡ u

−

aϕ(u)+b



(u)

≡ H (u, u

). (8.30)

The ordinary differential operator (8.30) is also a zero-invariant of the PDE (8.29).

This means that if, for a solution u(x , t),

H (u, u

) ≡ ϕ(u) + [aϕ(u) + b]c = 0inIR

for t = 0, (8.31)

then

H (u, u

) = 0inIR

for t > 0. (8.32)

Equation (8.32), (8.30) is integrated as a standard ODE (ϕ(u))



= aϕ(u) + b.This

yields the following exact solutions u(x, t) of (8.29).

(i) If a = 0, then

ϕ(u(x , t)) =

[ρ(x)e

− b], (8.33)

where ρ(x) is an arbitrary solution of the linear elliptic PDE

ρ +acρ = 0inIR

. (8.34)

(ii) If a = 0 (b = 0),then

ϕ(u(x , t)) = ρ(x) + bt, where ρ + bc = 0inIR

Besides such exact solutions, the SI (8.31) makes it possible to estimate more solu-

tions by using the inequality

−

aϕ(u)+b



(u)

≥ 0 (or ≤ 0) for t ≥ 0.

392 Exact Solutions and Invariant Subspaces

u(x , t)

−

−π

)

−

)

< t

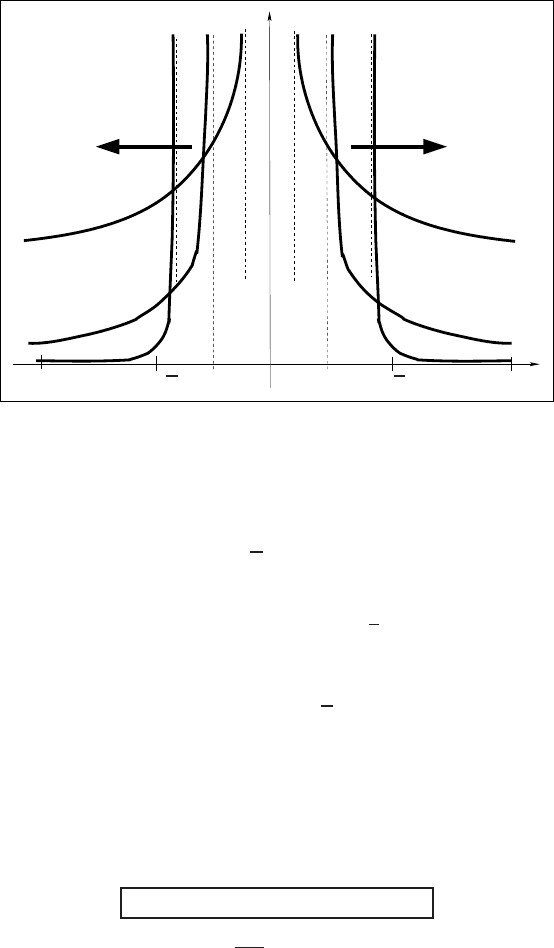
Figure 8.1 Stabilizing blow-up interfaces of the solution (8.36) of the PDE (8.35).

Blow-up interfaces. In the fast-diffusion case ϕ(u) =−u

−m

, m > 0, with a = b =

c = 1andN = 1, we obtain from (8.29) the 1D equation

=−(u

−m

)

(u − u

m+1

) + 1 − u

−m

. (8.35)

According to (8.33), taking ρ(x) = cosx yields the explicit 2π-periodic solution

u(x , t) = (1 − e

cosx)

−

, (8.36)

with blow-up interfaces propagatingas follows:

(t) =±cos

−1

−t

) →±(

)

∓

as t →∞.

Such unusual blow-up behavior is illustrated in Figure 8.1. The FBP with blow-

up interfaces and their dynamic equations are rigorously justiﬁed by the Sturmian

intersection comparison approach, [226, Ch. 7].

Invariant subspaces. It is easy to interpret these exact solutions in terms of invariant

subspaces. Consider the case a = 0. Using in (8.29) the Kirchhoff-type transforma-

tion v = aϕ(u) + b yields the following quasilinear equation:

= F[v] ≡ (v)(v +acv) + av, (8.37)

with the coefﬁcient (v) = ϕ



(ϕ

−1

(

v−b

)). Let us introduce the subspace

W ={ρ(x) : ρ solves (8.34)}. (8.38)

The existence of explicit solutions (8.33) is then a straightforward consequence of

the fact that W is invariant under F,i.e.,F[W ] ⊆ W, so this falls into the scope of

Chapters 1 and 2. Notice that dim W =∞if N > 1, and dimW = 2ifN = 1.