Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics
Подождите немного. Документ загружается.


7 Partially Invariant Subspaces and GSV 373
For α = 1, we have
u
2
k
− uk
= 0,
which yields the following hyperbolic equation:
u
tt
= F[u] ≡
a
1
+ a
2
u
2
u
x
x
+ µu
with the solution u(x, t) = C(t)x on the invariant subspace L{x} of F,where
C
= 2a
2
C
3
+ µC.
For α = 2, k satisfies
2u
2
k
+ uk
− k = 0,
giving the PDE
u
tt
= F[u] ≡
a
1
u +
a
2
√
u
u
x
x
+ 2µu
with exact solutions u(x , t) = C(t)x
2
,where
C
= 6a
1
C
2
+ 2µC.
In the case where
H (u) = 1,
we find k
− 3k
+ 2k = 0, and hence, the equation
u
tt
= F[u] ≡
a
1
e
u
+ a
2
e
2u
u
x
x
+ µ,
which admits the solution u(x, t) = ln x + D(t),where
D
= 2a
2
e
2D
+ µ.
Similarly, it is easy to consider other cases from (7.178). In the degenerate case
(7.179), where W = L{x, x
3
}, there occur two ODEs
2kHH
+ 3k
H
2
+ f
H − fH
= 0,
k
H +2k
H
= 0,
so taking H (u) = u yields the PDE
u
tt
=
a
2
−
a
1
u
u
x
x
− 2a
2
u ln u + a
1
+ a
3
u
possessing the solution u(x, t) = C(t)e
x
2
/2
,where
C
=−2a
2
C lnC + (a
2
+ a
3
)C.
7.6 A separation technique for the porous medium equation in IR
N
In this last section, we discuss a specific version of separation of variables. We deal
with the N-dimensional PME
v
t
= v
m
in IR
N
× IR
+
(v ≥ 0), (7.182)
© 2007 by Taylor & Francis Group, LLC

374 Exact Solutions and Invariant Subspaces
which, by the pressure transformation u =
m
m−1
v
m−1
, reduces to the quadratic form
u
t
= F
m
[u] ≡ (m − 1)uu +|∇u|
2
. (7.183)
The PME has m > 1, but the fast diffusion range m ∈ (0, 1) is also included, as well
as m = 0, corresponding to
v
t
= F
0
[v] ≡ ln v.
The pressure equation (7.183) with m = 0 is obtained by setting u =−
1
v
. Recall
also the PDE with the exponential nonlinearity
v
t
= e
v
,
which reduces to a similar quadratic pressure-like equation
u
t
= uu, where v = lnu.
According to Section 6.1, basic subspaces for the operator F
m
consist of either
linear, W
lin
= L{1, x
i
, i = 1, ..., N}, or quadratic functions, W
q
= L{1, x
i
x
j
}.On
each of the subspaces or on its sum, the PDE (7.183) reduces to finite-dimensional
DSs which can be integrated in quadratures (Section 6.1). We will use these sub-
spaces in what follows.
7.6.1 A separation problem
Let us look for solutions in the following form:
u(x , t) = [ f (x, t)]
p
+ g(x , t)(f > 0), (7.184)
where f and g aretwo unknownfunctionsfrom the abovespaces of linear orquadratic
functions, and p = 0, 1 is a parameter. Plugging into (7.183) yields a three-term ex-
pansion
f
p−1
p
− f
t
+ (m − 1)
gg +
1
p
f g
+ 2∇ f ·∇g
+(m − 1)(p −1)g
|∇ f |
2
f
+
−g
t
+ (m − 1)gg
+|∇g|
2
+ f
2p−1
p
(m − 1)f + (mp − m + 1)
|∇ f |
2
f
= 0.
(7.185)
This will be treated as a formal linear combination (with coefficients, depending on
x and t as parameters) of three vectors f
p−1
,1,and f
2p−1
. Assuming that
f (x, t), g(x, t) ∈ L{1, x
i
, x
i
x
j
} for all t ≥ 0 (7.186)
yields, in general, three PDEs on {f, g} if p =
1
2
,
−f
t
+ (m − 1)
gg +
1
p
f g
+ 2∇ f ·∇g
+(m − 1)( p −1)g
|∇ f |
2
f
= 0, −g
t
+ (m − 1)gg +|∇g|
2
= 0,
(m − 1) f +(mp − m + 1)
|∇ f |
2
f
= 0.
(7.187)
The case p =
1
2
(where f
2p−1
= 1) is special when the system contains two
© 2007 by Taylor & Francis Group, LLC
7 Partially Invariant Subspaces and GSV 375
equations,
− f
t
+ (m − 1)[gf + 2 f g] + 2∇ f ·∇g −
1
2
(m − 1)g
|∇ f |
2
f
= 0,
−g
t
+ (m − 1)gg +|∇g|
2
+
1
2
(m − 1) f +
1
2
(2 − m)
|∇ f |
2
f
= 0.
Roughly speaking, we are dealing with a kind of GSV on the set (a module) of
linear combinations W
2
= L{1,
√
f (x, t)}. In fact, we are already familiar with some
other representations of solutions, such as (7.184), given by extended fourth-order
polynomial subspaces studied in Section 6.2. By Proposition 6.24, for the operator
(7.183), such a subspace exists if
m =
N−2
N+2
.
In terms of representation (7.184), this gives the integer p = 2. The same p = 2
applies to the case m = 0, corresponding to the remarkable operator
F
rem
[u] = uu −|∇u|
2
in IR
2
. (7.188)
As was shown in Section 6.3, this admits subspaces of fourth-degree polynomials
and many others. It will be shown that p =
1
2
also makes sense for (7.188).
Nonlinear separation problem in the class of general quadratic forms. Consider
the most important and promising case of p =
1
2
, where (7.185) can be written in
the form of
1
− f
t
+ (m − 1)g f + 2(m − 1) f g + 2∇ f ·∇g
+
√
f
−2g
t
+ (m − 1) f + 2(m − 1)gg +2|∇g|
2
+ J = 0.
(7.189)
Here, J denotes two extra singular terms, which should satisfy the following prob-
lem of nonlinear separation (in other words, a “nonlinear eigenvalue problem”):
J ≡−(m − 1)g
|∇ f |
2
2 f
+ (2 − m)
|∇ f |
2
2
√
f
= λ
1
+ λ
2
√
f , (7.190)
where λ
1,2
are some constants or suitable functions.
Consider the problem (7.190) separately and independently of the PDE and its
symmetries. Let f = f (x) be a general quadratic form in IR
N
. Using an orthogonal
transformation, we reduce it to the diagonal form,
f =
a
i
x
2
i
.
Let us see if this can solve the eigenvalue problem (7.190). Thus
|∇ f |
2
= 4
a
2
i
x
2
i
,
so that, to resolve the singularities in the main first term in (7.190), there must exist
a constant a such that
a
2
i
= aa
i
for all i = 1, ..., N.
This gives two possibilities: either
Case (i): a
i
= 0forsomei,or
Case (ii): a
i
= a = 0foralli.
© 2007 by Taylor & Francis Group, LLC
376 Exact Solutions and Invariant Subspaces
We exclude case (i) that, as will be shown, leads to solutions belonging to lower-
dimensional subspaces in IR
N
, and corresponds to the same analysis in IR
K
with
some K < N,wherewetake
f = a
K
i=1
x
2
i
.
Case (ii) implies that f (x ) should be canonical, with the matrix being the multiple
of the identity one, i.e., aI. In this case,
|∇ f |
2
2 f
= 2a and
|∇ f |
2
2
√
f
= 2a
√
f , (7.191)
and this solves the separation problem (7.190).
Therefore, bearing in mind translations in x, we can take f (x, t) in the form of
f (x, t) = a(t)
(x
i
− ϕ
i
(t))
2
⇒ f = 2Na, (7.192)
and, in view of (7.191), we obtain from (7.189) the following system of PDEs:
f
t
= (m − 1)g f −2a(m − 1)g + 2(m − 1) f g +2∇ f ·∇g,
2g
t
= (m − 1) f +2a(2 − m) + 2(m − 1)gg +2|∇g|
2
.
(7.193)
The case where p =
1
2
for quadratic function f (x, t). Using formulae (7.191) and
(7.192) in the last equation in (7.187) yields another critical value of p,
2a
(m − 1)N + 2(mp − m + 1)
= 0,
i.e.,
p =
(m−1)(2−N )
2m
.
Hence, as for p =
1
2
, there occur two equations
f
t
= (m − 1)[gg + 2 f g] + 2∇ f ·∇g − 2a(m − 1)g,
g
t
= (m − 1)gg +|∇g|
2
+ a[(m − 1)N − m + 2].
This system is analyzed similarly to that for p =
1
2
, which we now begin to investi-
gate in detail.
7.6.2 Linear functions g(x , t)
Let us now return to p =
1
2
and consider the first simpler case, assuming that g ∈
W
lin
,i.e.,
g(x, t) = A(t) + C(t)x ≡ A(t) +
C
i
(t)x
i
.
Then g = 0, |∇g|
2
=|C|
2
, and system (7.193) takes a simpler form
a
(x
i
− ϕ
i
)
2
− 2a
ϕ
i
(x
i
− ϕ
i
)
= (m − 1)(N −1)2a
A +
C
i
x
i
+ 4a
C
i
(x
i
− ϕ
i
),
2
A
+
C
i
x
i
= 2a(N −2)(m − 1) + 2|C|
2
.
© 2007 by Taylor & Francis Group, LLC

7 Partially Invariant Subspaces and GSV 377
Equating the coefficients of monomials x
2
i
, x
i
, and 1 in both sides of the equations
yields the following system of ODEs:
a
= 0,
ϕ
=−βC,
ϕ · ϕ
= (β − 2)A − 2C · ϕ,
C
= 0,
A
= (β − 1)a +|C|
2
,
(7.194)
where β = 2 + (m − 1)(N − 1).Fromthefirst, fourth, and second ODEs,
a(t) ≡ a
0
, C(t) ≡ C
0
,ϕ(t) = Vt, with V =−βC
0
,
and the last equation gives
A(t) =
(β − 1)a
0
+|C
0
|
2
t. (7.195)
Finally, the third ODE in (7.194) implies that either
a
0
=|C
0
|
2
⇒ A(t) = β|C
0
|
2
t, (7.196)
or β = 1, i.e.,
m =
N−2
N−1
.
Assuming that m > 1, and denoting |V|
2
=
V
2
i
yields the solution
u(x , t) =
1
β
|V|
(x
i
− V
i
t)
2
−
V
i
x
i
−|V|
2
t
+
, (7.197)
where, as is usual for the PME, the positive part gives the weak solution with free
boundaries.This solutionis strictly positiveand, hence, is a smoothanalytic function
everywhere in IR
N
× IR
+
, except the unbounded segment of the straight line in IR
N
t
: x = Vs, with s ≥ t
(we are assuming that V
i
> 0), on which u = 0, and u(x , t) is Lipschitz continuous
in a neighborhood of the free boundary
t
. This interface has the cusp end-point
moving linearly with time,
x
cusp
(t) = Vt, (7.198)
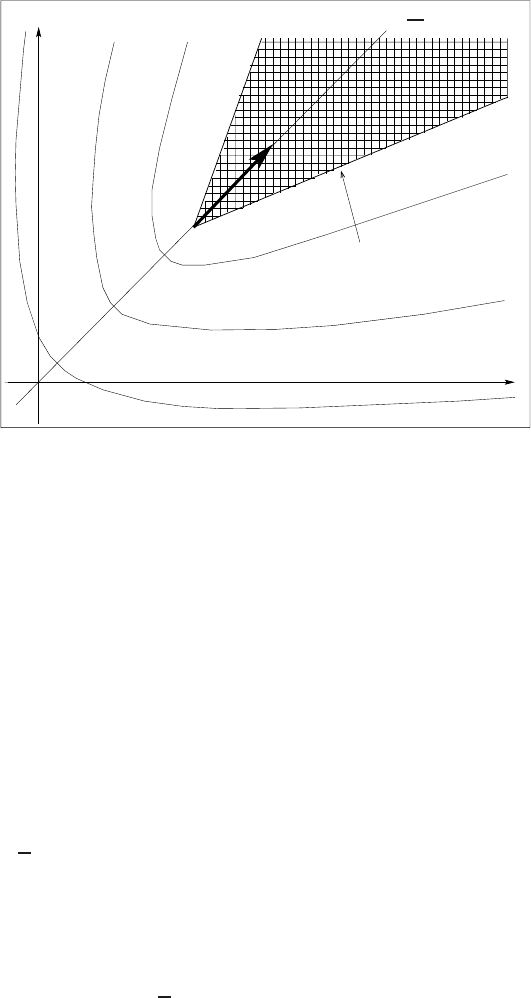
so the interface is not a smooth surface for all t > 0. In Figure 7.1 we present level
sets of this exact solution in IR
2
.
Let us next briefly consider two easy extensions of such solutions, exhibiting other
evolution properties.
Example 7.42 (Cusp localization) Consider the PME with a linear absorption,
v
t
= v
m
− v, m > 1. (7.199)
Then, setting v = e
−t
w yields
w
t
= e
−(m−1)t
w
m
.
Changing the time-variable
s =
1
m−1
1 − e
−(m−1)t
: IR
+
→
0,
1
m−1
© 2007 by Taylor & Francis Group, LLC

378 Exact Solutions and Invariant Subspaces
x
2
x
1
{u = 0}
x
2
=
V
2
V
1
x
1
Vt
t
0
Figure 7.1 The “razor blade” described by the explicit solution (7.197) in IR
2
.
returns us to the original PME
w
s
= w
m
that possesses the above explicit cusp solution (7.197). Hence, its spatial structure
remains the same, but the asymptotic behavior of this space-time pattern is different.
Since t =+∞corresponds to the finite s =
1
m−1
, it follows that
v(x , t) ≈ e
−t
w
x,
1
m−1
for t 1,
so, for the model (7.199), the cusp is localized and propagates through the finite
distance
1
m−1
|V| during the whole time of evolution t ∈ IR
+
.
Example 7.43 (Single point and conical singularities) Let us add a nonlinear re-
action or strong absorption term to the right-hand side of (7.182),
v
t
= v
m
+ µv
2−m
.
The pressure u will then solve the quadratic equation with an extra constant term,
u
t
= (m − 1)uu +|∇u|
2
+ µm.
Let us see how this affects explicit solutions with p =
1
2
. Solving the separation
problem(7.190),we thenaddan extrasingleterm into the second equationin (7.193),
so it has the form
2g
t
= (same terms) + 2µm.
This affects the last ODE in (7.194) only,
A
= (β − 1)a +|C|
2
+ µm.
© 2007 by Taylor & Francis Group, LLC
7 Partially Invariant Subspaces and GSV 379
Therefore, instead of (7.195),
A(t) =
(β − 1)a
0
+|C
0
|
2
+ µm
t,
so that the third ODE in (7.194) yields another relation between a
0
and C
0
,
a
0
=|C
0
|
2
−
µm
β−1
> 0.
Finally, this gives the same function A(t), as in (7.196).
Thus we obtain the explicit solution
u(x , t) =
1
β
|V|
2
− ε
0
(x
i
− V
i
t)
2
−
V
i
x
i
−|V|
2
t
+
, (7.200)
where
ε
0
=
µmβ
2
β−1
,
and we have to assume that |V|
2
>ε
0
. Though this solution looks similar to (7.197)
for the pure PME, it exhibits other evolution and interface properties.
Strong absorption: a single point singularity. Here, ε
0
< 0 in (7.200), so this ex-
plicit solution has the unique point of singularity x
cusp
(t) = Vt,atwhichu(Vt, t) =
0. As above, this cusp point moves linearly with time.
Reaction: a conical singularity. Here, ε
0
> 0, and hence,the supportof the solution
(7.200) is a conical surface K
t
in IR
N
composed of straight lines with the parametric
equations
x
i
− V
i
t = d
i
s,
where d ∈ IR
N
satisfies
|V|
2
− ε
0
|d|
2
=
V
i
V
j
d
i
d
j
.
K
t
has the vertex at the moving point (7.198). In IR
2
, the cone K
t
is the interior of
halves of two straight lines intersecting at x
cusp
(t) = Vt; see Figure 7.2.
7.6.3 Quadratic functions g(x, t)
Here, g is treatedas a general quadraticpolynomial.We havealready fixedthe canon-
ical structure of f in (7.192) that is necessary for resolving the separation problem
(7.190). From the first equation in (7.193), it is easy to see that the quadratic form of
g is then also diagonal and canonical. This reminds us of the well-known fact from
linear algebra saying that there exists an orthogonal transformation that simultane-
ously reduces a given quadratic form in IR
N
to the diagonal kind, and the second,
positive one, to the canonical kind.
Thus, take a general quadratic polynomial, which it is convenientto write down in
a form similar to (7.192),
g(x, t) = b(t)
(x
i
− ψ
i
(t))
2
+ A(t).
© 2007 by Taylor & Francis Group, LLC
380 Exact Solutions and Invariant Subspaces
x
2
x
1
{u = 0}
x
2
=
V
2
V
1
x
1
Vt
t
0
Figure 7.2 Moving triangular support described by the solution (7.200) of the PME with
source in IR
2
.
Substituting both expressions for f and g into (7.193) yields two equalities
−2a
(x
i
− ϕ
i
)ϕ
i
+ a
(x
i
− ϕ
i
)
2
= 2a(m − 1)(N −1)
b
(x
i
− ψ
i
)
2
+ A
+4(m − 1)Nab
(x
i
− ϕ
i
)
2
+ 8ab
(x
i
− ϕ
i
)(x
i
− ψ
i
),
−2b
(x
i
− ψ
i
)ψ
i
+ b
(x
i
− ψ
i
)
2
+ A
= (β − 1)a + 2b
2
(β + m − 1)
(x
i
− ψ
i
)
2
+ 2(m − 1)NAb.
Projecting both equations onto 1, x
i
,andx
2
i
respectively, we obtain the overdeter-
mined system
2aϕ · ϕ
+ a
|ϕ|
2
= 2a(m − 1)(N − 1)A
+2ab(m −1)(N − 1)a|ψ|
2
+ 4(m − 1)Nab|ϕ|
2
+ 8abϕ ·ψ,
ϕ
+
a
a
ϕ = 2b(m − 1)(N −1)ψ + 4(m − 1)Nbϕ + 4b(ϕ + ψ),
a
= 2[(m − 1)(N −1) + 2(β + m − 1)]ab,
2bψ · ψ
+ b
|ψ|
2
+ A
= (β − 1)a
+2b
2
(β + m − 1)|ψ|
2
+ 2(m − 1)NAb,
ψ
+
b
b
ψ = 2b(β + m − 1)ψ,
b
= 2b
2
(β + m − 1).
(7.201)
The last ODE is independentof the others, so we need to consider two cases:
© 2007 by Taylor & Francis Group, LLC
7 Partially Invariant Subspaces and GSV 381
Degenerate exponential case: β + m − 1 = 0. Assume that
β + m − 1 ≡ (m − 1)N +2 = 0,
i.e.,
m =
N−2
N
.
Then m ∈ (0, 1) for N ≥ 3andm = 0forN = 2, i.e., we deal with the fast
diffusion equation (7.182) rather than the PME for m > 1. The value m
∗
=
N−2
N
is
a well-known important critical exponent in the theory of the fast diffusion equation
(7.182). In particular, finite-time extinction of L
1
-solutions occurs precisely in the
range m ∈ (0, m
∗
), N ≥ 3, [37]. The critical m = m
∗
corresponds to the unusual
asymptotic behavior for t 1 in the Cauchy problem for (7.182); see [245, Ch. 6]
for further details concerning other critical issues of this exponent.
Then we take
b(t) ≡ b
0
= 0.
The third ODE in (7.201) implies that
a(t) = a
0
e
µt
, with µ = 2(m − 1)(N −1)b
0
=−
4(N−1)
N
b
0
.
The fifth equation reads ψ
= 0, so ψ = constant, and we set
ψ(t) ≡ 0 (7.202)
by translation. The second ODE gives
ϕ(t) = ϕ
0
e
νt
, with ν = 4[(m − 1)N +1]b
0
− µ =−
4
N
b
0
.
From the first equation in (7.201) we find
A(t) =−
N
4(N−1)
e
2νt
(µ + 2ν + 8b
0
)|ϕ
0
|
2
. (7.203)
The fourth ODE for A now has the form
A
=−4b
0
A −
N−2
N
a
0
e
µt
, (7.204)
and we want (7.203) to satisfy it. There are two possibilities.
Subcase I: N = 2, i.e., m = 0. Since −4b
0
= 2ν, (7.203) solves the ODE (7.204),
and the exact solution is obtained. This determines another invariant property of the
remarkable operator (7.188) in IR
2
besides those in Section 6.3.
Subcase II: N = 3, i.e., m =
1
3
.IfN = 2, we need
2ν = µ, or 2
−
4
N
b
0
=−
4(N−1)
N
b
0
,
which yields the only dimension
N = 3.
Substituting (7.203) into (7.204) yields the consistency condition
a
0
= 4b
2
0
|ϕ
0
|
2
.
The corresponding explicit solution of the PME (7.182) in IR
3
× IR
+
with m =
1
3
is
© 2007 by Taylor & Francis Group, LLC

382 Exact Solutions and Invariant Subspaces
as follows:
u(x , t) =
4b
0
|ϕ
0
|
2
e
−
8
3
b
0
t
x
i
− ϕ
i0
e
−
4
3
b
0
t
2
+b
0
|x|
2
−
1
2
b
0
|ϕ
0
|
2
e
−
8
3
b
0
t
.
Algebraic case: β + m − 1 = 0. The last equation in (7.201) yields
b(t) = c
0
t
−1
, where c
0
=−
1
2(β+m−1)
.
Similarly, from the fifth ODE, ψ
i
= 0, so (7.202) holds. The third equation yields
a(t) = a
0
t
ρ
1
, where ρ
1
=−
(m−1)(3N −1)+4
(m−1)N +2
.
We now use the second ODE of (7.201) to get that
ϕ
i
+ ρ
1
t
−1
ϕ
i
= 4[(m − 1)N +1]c
0
t
−1
ϕ
i
.
Integrating this linear first-order ODE gives
ϕ
i
(t) = ϕ
i0
t
ρ
2
, where ρ
2
=
(m−1)(N−1)+2
(m−1)N +2
.
Next, let us determine A from the first equation,
A(t) = ρ
3
|ϕ
0
|
2
t
2ρ
2
−1
, where ρ
3
=
1
2[(m−1)N+2]
. (7.205)
Finally, consider the fourth ODE that takes the form
A
= 2(m − 1)Nc
0
t
−1
A + [(m − 1)N −m + 2]a
0
t
ρ
1
, (7.206)
which is assumed to possess solution (7.205), i.e., on substitution,
(2ρ
2
− 1)ρ
3
|ϕ
0
|
2
t
2ρ
2
−2
= 2(m − 1)Nc
0
ρ
3
|ϕ
0
|
2
t
2ρ
2
−2
+ [(m − 1)N − m + 2]a
0
t
ρ
1
.
(7.207)
Subcase I: (m − 1)N −m + 2 = 0, i.e.,
m =
N−2
N−1
. (7.208)
Then (7.205) always solves (7.206).
Subcase II: (m − 1)N −m + 2 = 0. One needs
ρ
1
= 2ρ
2
− 2 ⇒ m =
3N−7
3(N−1)
,
as well as the following relation between constants that is obtained from (7.207):
a
0
=
3(N−1)
2(N−3)
2
|ϕ
0
|
2
(N ≥ 4).
In both subcases, the correspondingexplicit solutions of the PME (7.182) for m =
N−2
N−1
and m =
3N−7
3(N−1)
are given by
u(x , t) =
a
0
t
ρ
1
(x
i
− ϕ
i0
t
ρ
2
)
2
+
c
0
t
|x|
2
+ ρ
3
|ϕ
0
|
2
t
2ρ
2
−1
,
with the corresponding hypotheses on the parameters.
On solutions in IR
K
. Using a lower-dimensional quadratic form
f (x, t) = a(t)
K
i=1
(x
i
− ϕ
i
(t))
2
, with some K < N, (7.209)
© 2007 by Taylor & Francis Group, LLC
