Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics
Подождите немного. Документ загружается.

4 Korteweg-de Vries and Harry Dym Models 223
interface equation is obtained from (4.222) for any smooth solutions,
s
=−
1
u
x
u
t
= S[u] ≡−
3
4
(u
x
)
2
+
2
u
x
at x = s(t).
The governing interface equation for (4.223) is stationary, u
xx
=−2atx = s(t).
New HD-type models appear by adding other operators to the right-hand side,
preserving the invariant subspace. For instance, consider
v
t
= v
4
v
xxx
+ (v
3
)
xx
−
1
v
,
where setting v =
√
u yields the PDE with an extra quadratic operator,
u
t
= u
2
u
xxx
−
3
2
uu
x
u
xx
+
3
4
(u
x
)
3
+ 3
uu
xx
+
1
2
(u
x
)
2
− 2,
that preserves W
3
in (4.219). This has similar exact solutions and interfaces, and
exhibitstypicalsingularityphenomenaof extinction,quenching,and finite interfaces.
4.7.2 On the maximal regularity, oscillatory behavior, and the Cauchy problem
We use the TWs to check the maximal regularity for PDE (4.220),written nowin the
signed form for solutions of changing sign,
v
t
=|v|
4
v
xxx
−
v
|v|
2
. (4.226)
Substituting the TW solution v(x , t) = f (x − λt) yields
−λf
=|f |
4
f
−
f
| f |
2
for y > 0, f (0) = 0,
so that
f (y) =
√
y ϕ(s), where s = ln y, (4.227)
with the following ODE for the oscillatory component ϕ:
ϕ
−
3
2
ϕ
+
λ
|ϕ|
4
−
1
4
ϕ
+
3
8
ϕ +
λ
2|ϕ|
4
−
1
|ϕ|
6
ϕ = 0. (4.228)
For any λ ∈ IR , there exist constant solutions ±ϕ
0
,where
3ϕ
6
0
+ 4λϕ
2
0
− 8 = 0.
It is not difficult to show that these constant equilibria are unstable for both λ =±1.
Numerically, solutions of (4.228) are non-oscillatory and of constant sign (this is
associated with the strong singularity as ϕ → 0 of the coefficients in (4.228)).
The TW solutions(4.227) have the H¨older continuityexponent
1
2
attained at the in-
terface y = 0 which coincides with that given by the square root v =
√
u in (4.223).
These solutions are expected to exhibit the maximal regularity for PDE (4.226), so
(4.223) is assumed to correspond to the Cauchy problem. The non-changing sign
properties of ϕ(s) imply a possibility of constructing more general nonnegative so-
lutions of the Cauchy problem for PDE (4.220).
Let us briefly discuss a curious interface equation for the critical case n = 2,
v
t
= v
2
v
xxx
.
© 2007 by Taylor & Francis Group, LLC

224 Exact Solutions and Invariant Subspaces
We again use the TWs v(x, t) = f (x − λt) for deriving the interface equation, so
−λf
= f
2
f
,
and, on integration,
λ
f
= f
.
Hence, for λ<0, the behavior close to the interface at y = 0 is not oscillatory,
f (y) = y
2|λ||ln y|+... as y → 0
+
.
This asymptotic behavior can be used for deriving the dynamic interface equation,
as in Example 4.29. The formal analysis is easier, since the speed, λ, enters the first
expansion term; the proof is difficult and is an
OPEN PROBLEM.
4.7.3 On the fundamental solution
As usual, the existence of nonnegativesolutions does not mean positivity preserving
property in the Cauchy problem. For FBPs, the positivity can be enforced by free-
boundary conditions, as for the TFEs in Section 3.2.
Consider now the Cauchy problem for the signed HD-type equation (4.217) for
n ∈ (0, 1),
v
t
=|v|
n
v
xxx
in IR × IR
+
. (4.229)
We study finite propagation and oscillatory properties of its fundamental solution
b(x, t) = t
α
g(ξ), ξ =
x
t
β
, with α =−
1
3−2n
< 0,β=
1−n
3−2n
> 0, (4.230)
where g solves the following ODE problem:
A[g] ≡|g|
n
g
+ βg
ξ −αg = 0in IR ,
1
1−n
∞
−∞
|g|
−n
g dξ = 1. (4.231)
Solutions (4.230) are induced by the conservation law
d
dt
∞
−∞
|v|
−n
v dξ = 0, (4.232)
whichfollows from the PDE (4.229),providedthat the integralconverges.For n = 0,
(4.230) is the fundamental solution (4.138) of the operator in the linear PDE
v
t
= v
xxx
in IR × IR
+
. (4.233)
The normalization in (4.231)then becomes the standard condition of convergenceto
the δ-function as t → 0
+
,
∞
−∞
g dξ = 1.
By (4.139) (recall the reflection x → −x), the kernel g(ξ ) is oscillatory as ξ →+∞
and is not as ξ →−∞, with different asymptotics at these infinite interfaces.
We are going to detect similar oscillatory properties in the nonlinear case n ∈
0,
3
2
. The ODE (4.231) is integrated once by the conservation law, so
g
+
1
3−2n
|g|
−n
gξ = 0. (4.234)
Similar to solutions (4.74) of the signed K (2, 2) equation in Section 4.2.6, the fun-
© 2007 by Taylor & Francis Group, LLC
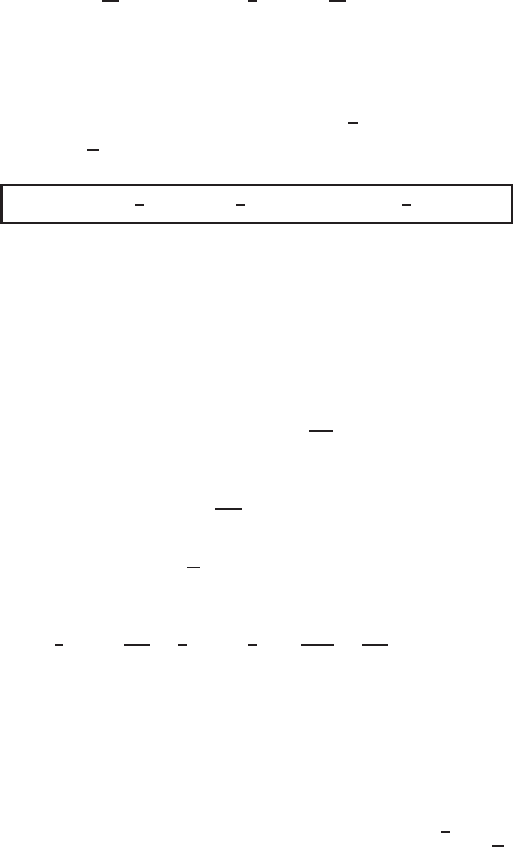
4 Korteweg-de Vries and Harry Dym Models 225
0 5 10 15 20 25
8
6
4
2
0
2
4
6
8
10
x 10
3
ξ
g(ξ)
n=1
n=0.5
n=0, Airy
Figure 4.22 Oscillations for ξ 1 of solutions of (4.234) with n = 0,
1
2
, and 1.
damental kernel g(ξ) is compactly supported on [ξ
0
, ∞), ξ
0
< 0, with positive ex-
pansion at the left-end interface,
g(ξ) =
n
2
|ξ
0
|
2(2−n)(3−2n)
1
n
(ξ − ξ
0
)
2
n
+ ... as ξ → ξ
+
0
.
The behavior as ξ →+∞is oscillatory and can be compared with that for the Airy
function in (4.139); see Figure 4.22.
4.7.4 Oscillatory solutions of higher-order Harry Dym-type equations
Similar phenomena take place for higher-order Harry Dym-type equations, such as
u
t
=|u|
n
u
xxxxx
.
For instance, introducing the oscillatory component into the TW-equation yields
−λf
=|f |
n
f
(5)
, f (y) = y
γ
ϕ(ln y) ⇒ P
5
[ϕ] =−λ
ϕ
+γϕ
|ϕ|
n
, (4.235)
where γ =
4
n
and the linear operator P
5
is as defined in Section 3.7, (3.157). There
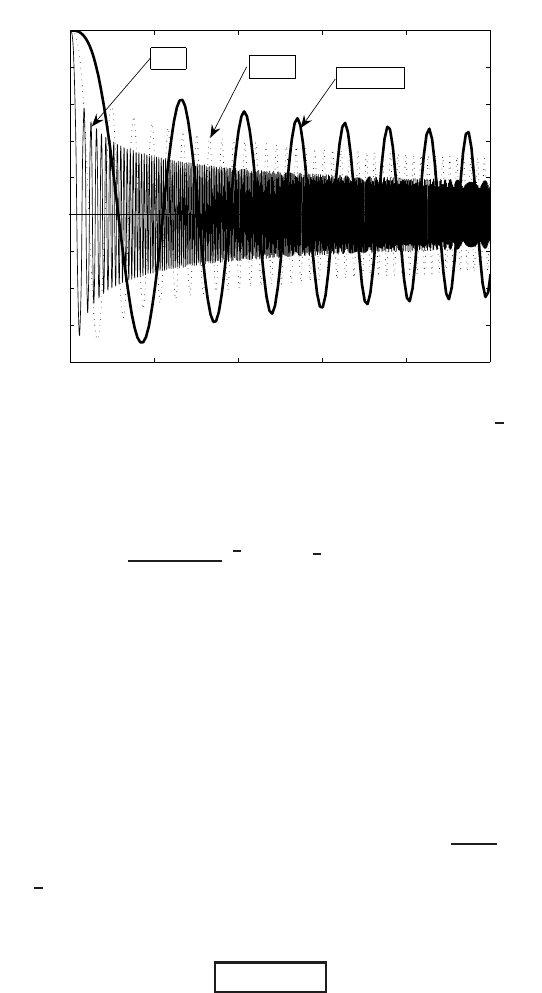
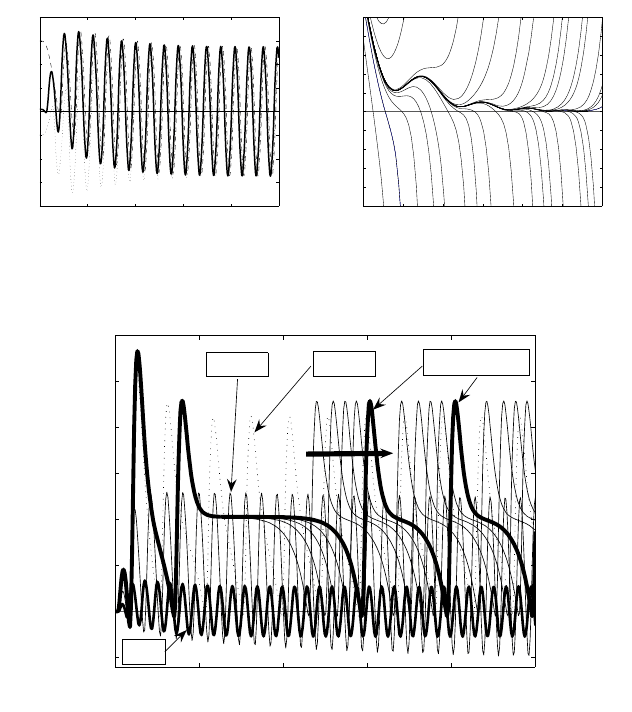
exists a stable periodic solution ϕ(s) for λ>0, at least for n ∈ (0, 1]; see Figure
4.23(a). We observed numerically the periodic behavior for all n ∈ (0, n
h
),where
n
h
= 1.08...
is a homoclinic bifurcationof periodic solutions,as shown in Figure 4.24. For λ<0,
a standard 1D shooting does not detect an unstable periodic solution. Figure 4.23(b)
shows a non-monotone separatrix behavior between flows of stabilization to two
constant equilibria ±ϕ
0
(this needs extra study).
© 2007 by Taylor & Francis Group, LLC
226 Exact Solutions and Invariant Subspaces
0 10 20 30 40 50
0.4
0.3
0.2
0.1
0
0.1
0.2
0.3
0.4
s
φ(s)
(a) n= 1,λ= 1
1.2 1.4 1.6 1.8 2 2.2 2.4
1
0.8
0.6
0.4
0.2
0
0.2
0.4
0.6
0.8
1
x 10
5
s
φ(s)
(b) n= 0.9, λ=−1
Figure 4.23 Solutions of (4.235) for n= 1, λ= 1 (a) and n= 0.9,λ=−1(b).
0 20 40 60 80 100
0.5
0
0.5
1
1.5
2
2.5
3
s
φ(s)
n=1.0830558
n=1
n=1.08
n=1.05
Figure 4.24 Deformation as n→ n
−
h
of periodic solutions of the ODE in (4.235) withλ= 1.
Cauchy data areϕ(0)= 10
−3
andϕ
(0)=ϕ
(4)
(0)= 0.
Remarks and comments on the literature
There are many excellent books on fundamental mathematical techniques and discoveries re-
lated to the KdV equation and other integrable PDEs; see e.g., Newell [436], Remoissenet
[487], and Ablowitz–Clarkson [2] for further references. We present below many classic and
recent references, including surveys on these subjects. Concerning other questions, which are
not directly related to integrability issues, such as existence, uniqueness, and regularity theory
for semilinear odd-order PDEs, these have been developed for at least forty years. We refer
to Lions [396, Ch. 3] for first results and key papers, and to Faminskii [179] for further ref-
erences. Semigroup approaches to the Cauchy problem for the KdV equation (4.1) were first
developed in papers by Kato and Faminskii–Kruzhkov in 1979 and 1980.
Soliton and KdV equation theory is one of most amazing scientific subjects relative to their
physical origin, applications, history, and discoveries during its mathematical development.
© 2007 by Taylor & Francis Group, LLC

4 Korteweg-de Vries and Harry Dym Models 227
The importance of solitary waves was emphasized by John Scott Russell’s experimental obser-
vations of waves in August of 1834 in the Union (Edinburgh–Glasgow) canal, [503]. Further
study were due to Airy (1845) [5] and Stokes (1847) [536]. See [511] and [2] for historical
details. The KdV equation (4.1) appeared in 1895, [354], though Boussinesq studied it earlier
in 1872 [75] and found the explicit cosh
−2
formula for its solitary-wave solution. The KdV
equation describes the evolution of weakly nonlinear and weakly dispersive waves in such
physical contexts as plasma physics, ion-acoustic waves, stratified internal and atmospheric
waves, etc. The term soliton is due to Zabusky and Kruskal [590], who, solving the KdV
equation numerically, made the discovery on the elasticity of interaction of its solutions. The
explicit form of N-soliton solutions for the KdV equation was obtained by the Baker–Hirota
bilinear method [22, 284]; see historical details in surveys in [2, 95, 250], in papers [3, 387]
and comments below. The integrable modified KdV (mKdV) equation
u
t
= u
xxx
+ 2u
2
u
x
,
is connected with the KdV equation (4.1) by the Miura transformation [426]
v = u
2
+
√
−3u
x
.
The history of various soliton-type solutions for the KdV and other integrable PDEs is
amazing. In 1903, Baker [22] derived the KdV hierarchy, including the fifth-order KdV equa-
tion
u
t
+ u
xxxxx
+ 30u
2
u
x
+ 20u
x
u
xx
+ 10uu
xxx
= 0inIR × IR ,
as well as the Kadomtsev–Petviashvili (KP) equation [308]
(u
t
+ 6uu
x
+ u
xxx
)
x
= u
yy
in IR
2
× IR .
The latter describes asymptotically weakly nonlinear and weakly dispersive long waves and is
obtained, in the weakly 2D limit, from the full water wave equations, where the surface ten-
sion is large. It also occurs for weak amplitude ion acoustic waves in an unmagnetized plasma.
Among Baker’s other results, there are the bilinear differential operator D (see (7.30)), maps
and transformations, which are referred to as Baker–Hirota transformations [20, p. 275], as-
sociated differential transformations (including, what we used to call, Cole–Hopf’s transfor-
mation), giving the bilinear form of the equations and hence explicit forms of hyperelliptic,
periodic multi-soliton solutions for a variety of integrable PDEs, etc.
†
Adetailedsurveyon
re-evaluation of the role of Baker’s hyperelliptic sigma function and other results in mod-
ern soliton theory is available in [415]; see also comments in [165] and [86] for a review of
the earlier part of Baker’s theory. Actually, Baker derived the key differential identity of the
hyperelliptic functions of arbitrary genus g (for odd, 2g+1, or even 2g+2, degree of the poly-
nomial f (x) of the corresponding hyperelliptic curve y
2
= f (x)) [22], which led to KdV
hierarchy and the KP equations of higher orders, but, explicitly, Baker presented these for the
genus g = 3 only. The curves of (2g+1) degree correspond to the KdV hierarchy, and the
ones of (2g+2) are associated with the KP equation. The list of PDEs for Baker’s ℘ function
also includes the Boussinesq equation; see [19]. In the 19th century, the development of the-
ory of hyperelliptic functions as generalizations of elliptic functions, as well as general alge-
braic and Abelian functions, was due to Weierstrass, Riemann, Abel, Klein, Jacobi, Poincar´e,
Burkhardt, Krazer, K¨onigsberger, Kovalevskaya, Hermite, Goursat, Appel, Tikhomandritskii,
†
“Surprisingly, even in the 19th century, there appeared most of the tools and objects in soliton theories,”
[417, p. 4322]. “It is not generally known that Baker solved a number of nonlinear integrable partial
differential equations... ,” [165].
© 2007 by Taylor & Francis Group, LLC
228 Exact Solutions and Invariant Subspaces
Brioschi, Frobenius, Stickelberger, Picard, Burnside, Kiepert, Bolza, and many other famous
mathematicians.
A direct relation of hyperelliptic functions to the KdV-type equations is seen from the defi-
nition of the classical Weierstrass ℘-function of genus g = 1, satisfying the ODE
(℘
(z))
2
= 4℘
3
(z) − g
2
℘(z) − g
3
, (4.236)
where the constants g
2,3
are called the invariants of ℘. One can derive from (4.236) other
ODEs for ℘, e.g.,
℘
(z) = 6℘
2
(z) −
1
2
g
2
and ℘
(z) = 12℘
(z)℘ (z),
where, after scaling, the latter is the stationary KdV equation. The first deep addition theorems
for such elliptic functions date back to 1849, [573].
Applications of Baker’s(orBaker–Akhiezer’s) functions for algebro-geometric, finite-gap
and elliptic solutions of fullydiscretized KP and 2D Toda equations are given in [357]. Several
facts from the modern finite-gap integration method of completely integrable PDEs, where
Baker–Akhiezer functions are key (see e.g., [35]), were discovered by Drach as early as 1918–
1919, [153, 154]. Drach also derived the stationary KdV hierarchy;
‡
see [35, p. 84], a detailed
survey in [250], and [311]. Earlier, in 1897, Drach was known for his general classification of
PDE systems by reducing these to a first or second-order systems in one independent variable.
The integrability of the associated linear spectral problem for the fundamental -function
−u = λ
goes back to Ermakov (1880) [170], and is equivalent to the integrability of Ermakov–Drach’s
equation
ψ
− (u + λ)ψ =−
µ
2
ψ
3
.
Concerning elliptic solutions of the stationary KdV hierarchy, or, equivalently, elliptic finite-
band potentials, q, for the linear Schr¨odinger operator L =
d
2
dx
2
+q(x), the famous finite-gap
example of the Lam´e potential
q(x) =−s(s + 1)℘ (x + ω
3
), s = 1, 2, ... ,
with fundamental half periods ω
1
∈ IR and ω
3
∈ iIR , found by Hermite and Halphen in the
1870s and 1880s, remained the only explicit potential for almost a century; see [35, p. 81,
p. 259], [250, Sect. 2.8], and [36, Sect. 4.2]. For another well-known example of integrable
PDEs, which can be solved in terms of linear problems with spectral parameters on an elliptic
curve, such as the Krichever–Novikov (KN) equation [356]
u
t
=
1
4
u
xxx
+
3[1−(u
xx
)
2
]
8u
x
−
3
2
℘(2u)(u
x
)
3
, (4.237)
related linear spectral problems for third-order operators were studied by Halphen in 1884,
[36, p. 302]. Particular degenerate cases of (4.237) are mapped to the Schwarzian KdV (SKdV)
equation
z
t
z
x
=
1
4
{z, x}≡
1
4
z
xxx
z
x
−
3
2
(z
xx
)
2
(z
x
)
2
,
with the Schwarzian derivative on the right-hand side. Notice that this equation is quadratic
‡
“It appears he was the first to make the explicit connection between completely integrable systems and
spectral theory,” [250, p. 288]. ”It is amazing that this remarkable work containing the constructions
rediscovered in connection with the study of the KdV equation by Dubrovin, Its, Matveev, Gel’fand,
Dikii is referred to very early in the modern literature,” [35, p. 85].
© 2007 by Taylor & Francis Group, LLC

4 Korteweg-de Vries and Harry Dym Models 229
(bilinear). Baker’s functions associated to the Lax equations, which determine the KP hierar-
chy of several variables, were studied in [377], where earlier references are given.
Exact solutions of the mKdV equation via Weierstrass σ and ℘-functions for the case of
genus one and via Baker’s hyperelliptic sigma functions for genus two were described in [417],
where hyperelliptic solutions for arbitrary genus were also constructed by using Weierstrass
al-function. Papers [86, 36] (here Kleinian functions are used as logarithmic derivatives of the
hyperelliptic σ -ones) and [415]–[417] contain detailed explanations concerning the signifi-
cance of hyperelliptic function theory from the nineteenth century, and especially of Baker’s
functions, for modern soliton theory. “...Miura transformation is a connection between the
worlds of ℘ and the al. I think that the researchers in the 19th century might have implicitly
already recognized these facts,” [417, p. 4332].
A detailed overview of elliptic algebro-geometric solutions of the KdV and Ablowitz–
Kaup–Newell–Segur (AKNS) hierarchies of integrable PDEs is available in [250], where spe-
cial attention is paid to classical Floquet, Hermite, and Picard theories. In particular, it was
emphasized there that the questions of stationary Lax equations [P, L] = 0oncommutingor-
dinary differential expressions (P, L) (the Lax pair) were raised by Floquet in 1879, and again
considered by Wallenberg in 1903 and Schur in 1905. The criterion for commutativity of dif-
ferential operators was established by Burchnall and Chaundy in the 1920s, and got further
development later, including the work by Baker in 1928, simplifying these results; see also
by H.F. Baker “Abelian Functions–Abel’s Theorem and the Allied Theory Including the The-
ory of the Theta Functions”, Cambridge, 1897... ,” [109, p. 112]. This book was republished
by Cambridge Univ. Press in 1995.
§4.1.Many exact solutions of various related nonlinear PDEs can be found by singularity
analysis; see [137]. Moving periodic soliton-like solutions (4.5) were introduced in [232, 217].
Exact solutions on invariant subspaces and sets for semilinear third-order PDEs are given in
[593]; see also [268] for a more recent work on the Lie point symmetries classification of the
KdV-type equations
u
t
= u
xxx
+ F(x, t, u, u
x
, u
xx
).
§4.2.Various families of quasilinear third-order KdV-type equations can be found in [128],
where further references concerning such PDEs and their exact solutions can be found. Higher-
order generalized KdV equations are of increasing interest; see e.g., the quintic KdV equation
in [296] and [583], where the seventh-order PDEs are studied. For the K(2, 2) equation (4.14),
the compacton solutions were constructed in [491]. More general B(m, k) equations
u
t
+ a(u
m
)
x
= µ(u
k
)
xxx
also admit simple semi-compacton solutions [498], as well as the Kq(m,ω)nonlinear disper-
sion equation (another nonlinear extension of the KdV) [491]
u
t
+ (u
m
)
x
+ [u
1−ω
(u
ω
u
x
)
x
]
x
= 0.
Setting m = 2andω =
1
2
yields a typical quadratic PDE
u
t
+ (u
2
)
x
+ uu
xxx
+ 2u
x
u
xx
= 0
possessing solutions on standard trigonometric-exponential subspaces. Combining the K (m, n)
and B(m, k) equations gives the dispersive-dissipativity entity DD(k, m, n) [493]
u
t
+ a(u
m
)
x
+ (u
n
)
xxx
= µ(u
k
)
xx
that can also admit solutions on invariant subspaces for some values of parameters.
© 2007 by Taylor & Francis Group, LLC
[109, p. 87]. “Theta solutions of the Sin-Gordon equation ... can be seen in Ch.11 of the book

230 Exact Solutions and Invariant Subspaces
Concerning the interface and approximation problems posed in Example 4.8 and others,
for a class of degenerate third-order PDEs, a detailed approach concerning ODE analytic ap-
proximations of various non-smooth patterns (e.g., compactons or peakons) was performed in
[388], establishing that some of these solutions can be approached by approximating analytic
profiles. Among other things, this analysis reveals that, for higher-order PDEs and ODEs, such
an approach can be practically intractable. Ideas of maximal regularity and homotopy families
of PDEs help to detect correct classes of solutions of the Cauchy problem. For higher-order
degenerate PDEs, such solutions are often of changing sign, which sometimes contradicts
physical meaning and motivations of the models, but is a non-avoidable feature. Various FBPs
can be dealt by von Mises transformations locally, near singularities, though the complexity
of computations and analysis increase dramatically with the order of PDEs involved.
Concerning the ε-regularization aspects of proper (weak) solutions in Section 4.2.4, note
that such difficulty occurs for semilinear higher-order parabolic PDEs with non-smooth coef-
ficients, e.g.,
u
t
=−u
xxxx
−|u|
p−1
u, where p ∈ (−1, 1). (4.238)
Since the strong absorption term −|u|
p−1
u is not Lipschitz continuous at u = 0forp < 1and
even singular or discontinuous for p ≤ 0, for construction of proper solutions, the following
analytic ε-regularization is natural [227]
|u|
p−1
u → (ε
2
+ u
2
)
p−1
2
u (ε > 0).
This gives the necessary smooth family {u
ε
(x, t )} of classical solutions. Equation (4.238)
admits compactly supported solutions of changing sign. For p ≤−1, the limit ε → 0 implies
nonexistence of a proper solution, which is actually u ≡ 0, meaning that the limit proper
semigroup is discontinuous at t = 0; see further examples in [226, Ch. 7 and 10].
§4.3.The Florin FBP for the heat equation in IR
N
(introduced by Florin in 1951) includes
the free-boundary conditions of the form
u = 0and
∂u
∂n
=−1;
see [190] and references in [226, Ch. 8]. The FBP setting for the fifth-order equation (4.76)
uses a second-order Florin-type condition. Third and higher odd-order evolution PDEs also
appear in the hierarchy of surface evolution equations [428, 82]
V
n
≡ N
t
= BD
l
s
κ,
where V
n
is the local normal velocity of the surface, κ is the curvature of the surface, and s is
the arclength. The case l = 3 governs long frontal waves in the quasigeostrophic approxima-
tion [471]. Concerning the relation between many integrable PDEs and the motion of curves
on the plane in the various Klein geometries, see [120] and references therein.
§4.4.There is a large amount of literature devoted to existence, uniqueness, and asymptotic
behavior for the KdV and KP-type equations; see [381, 69, 179]. Delicate structures of blow-
up similarity solutions of the mKdV equation (4.133) with m ≥ 4 are described in [70].
§4.5.This study will be continued in Section 6.7, where further references are given. Com-
pactons of the type (4.178) was first detected by Rosenau [494, p. 197].
§4.6.Equation (4.181) can be considered as an integrable modification of the PBBM equation
(4.201) (reduced to it by omitting the last two terms on the right-hand side). It was shown that
(4.181) admits solitary-wave solutions with compact support. On the other hand, (4.181) is
the nonlinear dispersive counterpart of the KdV equation (4.1) and forms the first member of
the bi-Hamiltonian hierarchy; see an explicit algorithm in [449] based on the bi-Hamiltonian
representation of the classically integrable systems.
© 2007 by Taylor & Francis Group, LLC

4 Korteweg-de Vries and Harry Dym Models 231
Equation (4.192) was originally obtained by Fuchssteiner [209] by the method of recur-
sion operators. As was first noticed by Fuchssteiner and Fokas in [212], it is a bi-Hamiltonian
generalization of the KdV equation with infinitely many conservation laws and is formally
integrable. It was subsequently derived via physical principles in [94], where its further new
remarkable properties were established (see details on the derivation of the FFCH equation as
a shallow water model in [306]). With the omission of the last two terms (formally, of higher
quadratic asymptotic order for small solutions), (4.192) turns into the PBBM equation (4.201)
which is not known to be integrable. This PDE also happens to be another (together with
(4.181)) first member of the bi-Hamiltonian hierarchy of the KdV equation [449]. A principal
feature of (4.192), observed first in [94], is that it admits soliton solutions with sharp corners.
The resulting solutions, consisting of a collection of peaked waves, were called multipeakons
in [94]. An algorithm for constructing solutions of the shallow water equation (4.192) by
the inverse scattering technique and a Liouville transformation using the link with the KdV
equation is explained in [96] (construction of N-soliton, cuspon, and soliton-cuspon solutions
leads to difficult algebraic equations that can be studied numerically, [184]). A full classifica-
tion of weak discontinuities (including various types of cuspons and stumpons) admitted by
the traveling wave solutions u(x, t) = ϕ(x −ct) of the FFCH equations is performed in [379].
Conservation laws are studied in [380].
Concerning uniqueness for PDEs, the most well-known example is the heat equation
u
t
= u
xx
,
where the famous Tikhonov–T¨aklind uniqueness class was obtained in the 1930s [552, 548].
Uniqueness of the solution of the Cauchy problem takes place in the class
{|u(x, t )|≤e
|x |h(|x|)
},
with any positive increasing function h(s) satisfying Osgood’s criterion
∞
ds
h(s)
=∞.
We refer to results and the literature in [443], where a detailed analysis of uniqueness classes
is performed for the second and higher-order parabolic PDEs and systems by energy estimates
based on Saint-Venant’s principle.
As far as singularity formation phenomena in integrable PDEs (e.g., formation and exis-
tence of soliton solutions with non-analytic singularities) are concerned, it seems that the first
example was proposed in [300] (see also [568]), where the following equation:
u
xt
+
u
xx
(1+(u
x
)
2
)
3/2
xx
= 0 (4.239)
was derived as a model of nonlinear transverse oscillations of elastic beams. Due to the
gradient-dependent nonlinearity, this equation can admit cuspons, i.e., weak solutions hav-
ing cusps, where u
x
=∞, which propagate with finite speed. In particular, it was shown in
[300] that there exist such traveling wave solutions
u(x, t) = g(η), with η = x ± λt,
where g solves a nonlinear ODE with the following behavior at the cusp at η = 0:
g(η) =
2
λ
− (
2
λ
)
1
4
√
|η|(1 + o(1)) as η → 0 (λ > 0).
These solutions are H¨older continuous with exponent
1
2
. We refer also to cusp structures re-
vealed by N-soliton solutions of (4.192), corresponding to completely integrable Hamilto-
nian ODEs, in [94, 6, 31] and [449]. This model and the singularity formation study answer
© 2007 by Taylor & Francis Group, LLC

232 Exact Solutions and Invariant Subspaces
Whitham’s suggestion [575] to find mathematical PDEs for shallow water waves that include
the wave breaking phenomena.
Analysis of the bi-Hamiltonian structure of the FFCH and Hunter–Saxton equations can be
found in [211, 335].
An advanced theory of local solvability of the FFCH equation can be found in [387] (the
regularization term εu
xxxxt
is used, local existence and blow-up in Sobolev spaces H
s
for
s >
3
2
, and some results for s ≤
3
2
), [134] and references in [136] (using Kato’s semigroup
approach to (4.198), local and global H
1
-theory, and uniqueness), [579] (parabolic regulariza-
tion εu
xx
in (4.198), global H
1
-theory for arbitrary data, with no uniqueness, recovering an
analogy of Oleinik’sentropy“E-condition” for shocks [441]), [364] (existence, uniqueness,
and blow-up for initial-boundary value problems). See details on the propagation of weak sin-
gularities in [135] and on the orbital stability of multipeakons in [136]. In general, the FFCH
(4.192) and similar PDEs belong to the class of the third-order quasilinear pseudo-KdV-type
equations and their “pseudo” nature, via the integralrepresentations with positive compact ker-
nels, such as in (4.198), ensures solvability and uniqueness (cf. the PBBM equation (4.201)
which has smoother solutions than the conservation law u
t
= uu
x
).
The PBBM equation, written in the form of
u
t
+ u
x
+6uu
x
− u
xxt
= 0
possesses a family of solitary wave solutions
u(x, t) =
2α
2
1−4α
2
sech
2
[α(x −λt )],
where λ =
1
1−4α
2
. The PDE is not integrable, so their interaction is not elastic.
Well-developed mathematical theory of the FFCH equation (4.192) shows that it is precisely
the PDE exhibiting all the desired properties of integrability, breaking of waves, and existence
of solitons. The simpler Whitham equation (1967) [575] with a linear non-local term
u
t
+uu
x
+
IR
k
0
(x − ξ)u
x
(ξ, t) dξ = 0,,
where the kernel is given by
k
0
(x) =
1
2π
tanξ
ξ
e
iξ x
dξ,
though admitting the effect of breaking of waves, does not have a soliton interaction of its
traveling waves; see references in [136]. The corresponding generalized PDE with the extra
fifth-order term u
xxxxx
is globally well-posed for any H
1
-data in the appropriate Bourgain
function space X
1
, [283]. Higher-dimensional versions of various shallow water equations,
further extensions, history, and references on more abstract frameworks are available in [290].
There exists another integrable PDE from the family (4.193), (4.194), the Degasperis–
Procesi equation
u
t
− u
xxt
=−4uu
x
+ 3u
x
u
xx
+ uu
xxx
;
see [145] and early references therein (no other integrable equations exist in this family, which
was introduced in [491]). On existence, uniqueness (of entropy weak solutions in L
1
∩ BV),
parabolic ε-regularization, Oleinik’s entropy estimate and generalized PDEs, see [131].
It is curious that the whole three-parameter family of such PDEs indicated in Proposition
4.44 admits the single peakon solution (4.196). Restricting our attention to the one-parameter
family of equations introduced in [145],
u
t
−u
xxt
= F
β
[u] ≡−(1 +β)uu
x
+ βu
x
u
xx
+ uu
xxx
, (4.240)
© 2007 by Taylor & Francis Group, LLC
