Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics

Подождите немного. Документ загружается.

4 Korteweg-de Vries and Harry Dym Models 233

there exist the multipeakon solutions (4.197), where, for β = 3, 2, the functions {q

, p

} are

not canonical variables, and the corresponding DS takes a similar form



˙q

∂ H

∂p

˙p

=−(β − 1)

∂ H

∂q

with the same “Hamiltonian” (4.200) (the canonical Hamiltonian form exists only in the spe-

cial cases β = 3 and 2). This example shows the principal fact that integrability is not a nec-

essary condition for the existence of countable families of N-solitons for arbitrary N, though,

clearly, for β = 3, 2, explicit formulae for {q

(t), p

(t)} can be found by inverse scattering

techniques that describe the peakon interactions more clearly and in greater detail.

The Fornberg–Whitham (FW) equation

− u

xxt

= uu

xxx

− uu

+ 3u

− u

that describes qualitative behavior of wave-breaking [574], contains the quadratic operator

from (4.240) with β = 3, so scaling x → 2x leads to

− 2u

xxt

= F

[u] −4u

. (4.241)

Looking for the 1-peakon solution

u(x, t) = C

(t)e

+ C

(t)e

−x

∈ W

andbearinginmindthatF

= 0onW

, we obtain linear ODEs for the coefﬁcients and the

general solution of (4.241) u(x, t ) = Ae

x−

+ Be

−(x−

, where A and B are arbitrary

constants. This gives the well-known 1-peakon pattern [195]

u(x, t) = Ae

−|x−

which, unlike the above tautological PDEs on W

,hastheﬁxed wave speed λ =

For the Hunter–Saxton equation (4.209), its reduction to a ﬁnite-dimensional completely

integrable Hamiltonian system with phase space, consisting of piecewise linear solutions

(4.210), was ﬁrst discussed in [295]; see also references given in [32]. Another more gen-

eral water wave equation takes the form [575]

+ η

xxx

+ 6ηη

+ ε(

xxxxx

+ 10ηη

xxx

+23η

− 6η

) = 0 (4.242)

(terms of the order O(ε

) are omitted), where y = η(x, t) denotes the position of the free

surface of a body of water, considered as an inviscid incompressible ﬂuid, lying above a hor-

izontal ﬂat bottom. This PDE is associated with the generalized FFCH equation (generalized

integrable KdV equation)

+ u

xxx

+ 6uu

−

ε(u

xxt

+ 2uu

xxx

+ 4u

) = 0, (4.243)

in the sense that the function

η = u +ε(

−

−1

is integration in x) solves (4.242); see [193] for other examples and related references

therein. The generalized SKdV equation (4.211) admits a wide range of moving blow-up and

soliton-like solutions, depending on two arbitrary functions [247].

Further references and some mathematics on the Green–Naghdi equations (4.212) can be

found in [386]. Concerning higher-order PDEs, we mention the Kawahara equation (1972)

+ uu

+ αu

− u

xxxxx

= 0

234 Exact Solutions and Invariant Subspaces

that describes propagation of long waves under ice cover in ﬁnite depth liquids and gravity

waves on liquid surfaces with surface tension. The Kawamoto equation [330]

= u

xxxxx

+ 5u

xxxx

+ 10u

xxx

has higher-degree algebraic terms, as well as Lax’s seventh-order KdV equation

+ [35u

+ 70(u

+ u(u

)

) + 7(2uu

xxxx

+ 3(u

)

+ 4u

xxx

) + u

xxxxxx

]

= 0,

and the seventh-order Sawada–Kotara equation

+ [63u

+ 63(2u

+ u(u

)

) + 21(uu

xxxx

+ (u

)

+ u

xxx

) + u

xxxxxx

]

= 0.

One and two-soliton solutions of the standard form, which can be also derived by Baker–

Hirota-type methods of the multi-parameter family of equations

u + r

xxx

)

= 0

(4.244)

were constructed in [595] by using a modiﬁcation of the dressing method that was originally

developed for application to completely integrable nonlinear PDEs.

In connection with solutions (4.216) in Example 4.55, notice that similar mixed subspaces

appear for the positon and negaton solutions of the KdV equation, u

+ 6uu

+ u

xxx

= 0,

which, in terms of the function v = 2(lnu)

for the bilinear representation, take the form

v(x, t ) = sin(px + p

t) − p(x + 3p

t) ∈ L{1, x, cos px, sin px},

v(x, t) = sinh(px − p

t) + p(x − 3p

t) ∈ L{1, x, cosh px, sinh px},

respectively, where p = 0. Positon solutions of the KdV equation (soliton-positon interaction)

have been recognized since the 1970s as solutions with inverse square singularities and slow

decay at inﬁnity. See ﬁrst results on rational solutions induced by polynomials obtained in

1978 by Ablowitz and Satsuma, Adler and Moser (see survey [407]) and Bordag and Matveev

[72]; [16] (one-positon solution was studied by a variant of the inverse scattering method), and

[418]. On two and higher-order positons, see [419, 407]. Negatons were obtained in [485].

Both types of solutions belong to the class of generalized Wronskian solutions of the bilinear

KdV equation (i.e., (0.31) of the Introduction) introduced in [204, 418]. This approach is a

generalization of the Wronskian representation of multi-solitons invented by Satsuma [515].

According to Matveev’s Wronskian formula, positons correspond to choosing eigenfunctions

with positive eigenvalues of the Schr¨odinger spectral problem. For the sine–Gordon equation

− u

= sinu,

positons were constructed by Beutler [60]. These solutions, belonging to a combination of

polynomial and trigonometric/exponential subspaces, exist for other integrable 1D and 2D

PDEs; see [125].

§4.7.Further references on the Dym hierarchy of integrable PDEs are available in [6] and

[30], where the acoustic scattering theory is developed.

Open problems

• These have been formulated throughout the chapter in Examples 4.3, 4.7, Section

4.2.2, Example 4.8, Sections 4.2.4 and 4.2.5,Examples 4.9, 4.28, 4.29, 4.31, Section

4.5, Examples 4.38, 4.41, 4.43, 4.45–4.48, 4.50–4.52, 4.56, and in Section 4.7.2.

CHAPTER 5

Quasilinear Wave and Boussinesq Models in

One Dimension. Systems of Nonlinear

Equations

This chapter completes the description of exact solutions on invariant subspaces of 1D non-

linear evolution equations. We consider quasilinear wave and Boussinesq models. In the last

section we study systems of evolution PDEs of various types.

5.1 Blow-up in nonlinear wave equations on invariant subspaces

5.1.1 Basic quasilinear wave models

We consider quasilinear PDEs which are second-order in the time variable, i.e., con-

tain the derivative u

. This class includes the well-known second and higher-order

PDEs of hyperbolic type, which provideus with interesting new examples of forma-

tion of evolution singularities. There are many applications of quasilinear hyperbolic

equations possessing exact and explicit solutions. We present a few of equations

below and include more referencesin the Remarks. In particular, Zabusky [589] pro-

posed to use the hyperbolic equation

= k(u

as a model for the dynamicsof nonlinear strings. In this context,it is worth mention-

ing the standard derivation of the vibrating string equation by Newton’s Second Law

for a homogeneous thin string. Under the assumption that Hook’s Law applies, this

yields, in the dimensionless form, the quasilinear PDE



√

1+(u

)



For small deviations from equilibrium, where (u

)

& 1, we arrive at the canonical

linear wave equation

= u

As another example, wave operators appear from equations for steady transonic

gas ﬂow (here t = y is the vertical coordinate)



= v

+ uu

= 0,

so, replacing u → −u, and excluding v yields the quadratic wave equation

= (uu

)

. (5.1)

236 Exact Solutions and Invariant Subspaces

It is of hyperbolictype in the positivity domain of the solution {u > 0}. More general

quasilinear wave models come from the 1D gas dynamics equations



+ (ρv)

= 0,

+ vv

= 0,

where the pressure p = p(ρ) is a given monotone increasing function of the density.

Introducing the stream function ψ(x, t) such that

ρ = ψ

,ρv=−ψ

and using the independent variables {ψ, t},whereu(ψ, t) =

,weﬁnd that u(ψ, t)

satisﬁes the hyperbolic PDE











In applications, we will study more general quasilinear wave equations, such as

= (ψ(u)u

)

+ (lower-order terms),

= (ψ(u

))

+ (lower-order terms),

with different types of coefﬁcients ψ(s), arising in nonlinear wave theory. Similar

to other evolution models, the hyperbolic PDEs can create evolution singularities,

exhibiting different asymptotic patterns.

5.1.2 Stability of blow-up on invariant subspaces

Example 5.1 (Blow-up, localization, stability) Let us begin with the following

quadratic wave equation with source (a force term):

= F[u] ≡ (uu

)

+ 2u

≡ uu

+ (u

)

+ 2u

, (5.2)

where F is a typical second-orderoperatorfrom Section 1.4. In the positivity domain

{(x, t) ∈ IR

: u > 0}, equation (5.2) is of hyperbolic type, where the Cauchy prob-

lem can be posed and, by the Cauchy–Kovalevskaya Theorem, there exists a unique

local analytic solution in some neighborhood of any point of strict hyperbolicity. On

the other hand, in the negativity domain, {(x, t) ∈ IR

: u < 0}, (5.2) is of elliptic

type, where a boundary-value problem is natural. In general, (5.2) is a quasilinear

elliptic-hyperbolic equation for which existence-uniquenesstheory is notwell devel-

oped.Exact solutions may help us to understandits singularities and main difﬁculties

of the analysis.

We begin by describing blow-up properties of solutions

u(x , t) = C

(t) + C

(t) cos x (5.3)

of (5.2), which belong to the subspace W

= L{1, cos x } that is invariant under the

quadratic operator F. The correspondingDS takes the form





= 2C

+ C



= 3C

(5.4)

Consider 1D invariant subspaces from W

. First of all, it is W

= L{1} on which

5 Quasilinear Wave and Boussinesq Models. Systems 237

u(t) = C

(t) is obtained from (5.3) for C

(t) ≡ 0, and the DS (5.4) reduces to



= 2C

. (5.5)

This is the simplestsolutionof the PDE, which does not depend on the space variable

x. Integrating (5.5) once via multiplying by C



yields that all the blow-up solutions

have the following behavior close to the blow-up time T :

(t) =

(T −t )

(1 + o(1)) as t → T

−

Other invariant subspaces appear in symmetric cases C

=±C

in (5.3) that give

= L



2cos

(

)



and W

−

= L



2sin

(

)



In both cases, setting C

=±C

in the DS (5.4) yields another ODE (cf. (5.5))



= 3C

⇒ C

(t) =

(T −t)

(1 + o(1)) as t → T

−

Choosing the explicit solution C

(t) = 2(T −t)

−2

leads to the 2π-periodic separate

variables similarity solution of the PDE on W

(x , t) =

(T −t )

4cos

(

Next, noting that u

, t) ≡ 0 at points x

= (2k + 1)π , we take the one-hump

(x , t) =



(T −t)

4cos

(

) for |x |≤π,

0for|x| >π,

(5.6)

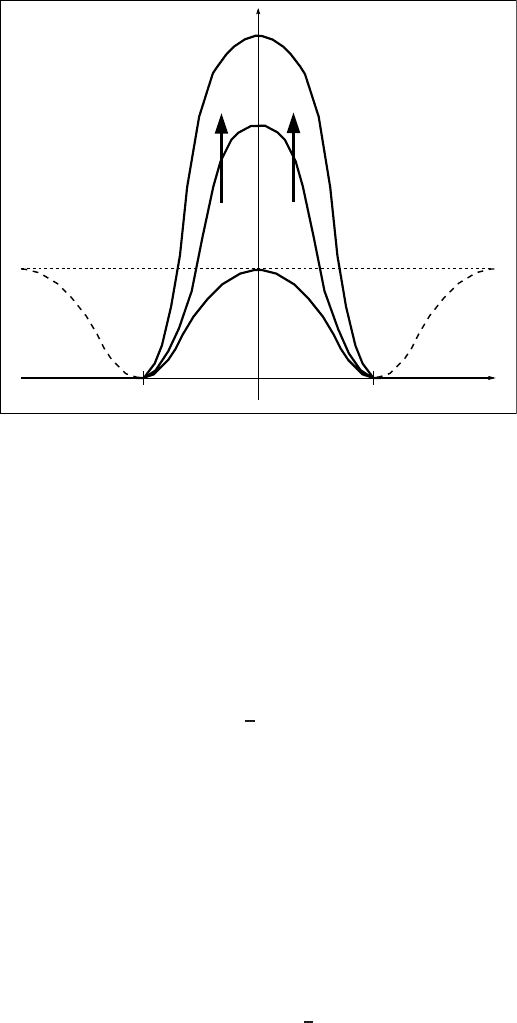
which is a localized standing wave (a kind of blow-up standing compacton); see

Figure 5.1. It exhibits regional blow-up in the interval (−π, π).ThenL = 2π is the

fundamental length.

The compactly supported function (5.6) is a standard weak solution of the Cauchy

problem for (5.2) in IR ×(0, T ) with corresponding initial data u

(x , 0), (u

)

(x , 0).

This is easy to check via multiplying the equation by a smooth test function and

integrating by parts. Of course, this does not mean that, for general initial data, the

quasilinear hyperbolic equation (5.2) admits sufﬁciently smooth nonnegative solu-

tions (actually, solutions may change sign and discontinuous shock waves may ap-

pear). In fact, we claim that the standing wave solution (5.6) with zero-ﬂux and zero

contact angle conditions is an exceptional one, so there are many other moving pat-

terns which propagate with shock waves (for instance, via TWs).

Nevertheless, the separate variables solution (5.6) is expected to describe a stable

generic blow-up behavior of this model. In a general setting, taking an arbitrary so-

lution u(x, t) (say, symmetric in x) blowing up at t = T , stability analysis assumes

showing stabilization of the rescaled function as τ =−ln(T − t) →+∞,

w(x,τ)= (T − t)

u(x , t) → g(x ) = 4cos

(

), (5.7)

where g is the similarity proﬁle given in (5.6). The rescaled equation for w is

ττ

+ 5w

= A[w] ≡ F[w] − 6w = (ww

)

+ 2w

− 6w. (5.8)

The passage to the limit τ →∞to establish (5.7) for a certain class of solutions is a

hard

OPEN PROBLEM.

238 Exact Solutions and Invariant Subspaces

u(x , t)

< t

< T

−π

Figure 5.1 Regional blow-up exhibited by the solution (5.6) on the interval (−π,π).

A comment on linear stability. Notice that even the linearized setting is not easy for

such hyperbolic PDEs and leads to

OPEN PROBLEMS of spectral theory of quadratic

pencils of linear operators. We perform some preliminary computations which will

help us later on to perform stability analysis on W

. Using the linearization in (5.8)

about the stationary similarity proﬁle, we set w(x ,τ)= g(x ) +Y (x,τ). This yields

the following linear hyperbolic equation:

ττ

+ 5Y

= A



[g]Y, (5.9)

where the second-order linearized operator A



[g] has the symmetric form



[g]Y = (gY )



+ (4g − 6)Y ≡



)



+ [g



+ 2(2g − 3)]Y. (5.10)

As usual, looking for separate variables solutions of (5.9),

(x ,τ)= e

(x )

yields the spectral problem



[g]ψ

= µ

, where µ

= λ

+ 5λ

. (5.11)

Here {µ

} and {ψ

} are eigenvalues and eigenfunctions of the linear operator A



[g],

but actually we deal with the simple quadratic pencil (λ

+ 5λ)I − A



[g]ofself-

adjoint operators.

According to classical theory of linear singular ordinary differential operators

[432], A



[g] admits a self-adjoint extension in the weighted space L

((−π, π))

with the positive weight ρ = g(x) ≡ 4cos

(

). Let us take the unique minimal

Friedrichs self-adjoint extension of the symmetric operator (5.10) that corresponds

to zero Dirichlet boundary conditions at regular end-points; see Birman–Solomjak

5 Quasilinear Wave and Boussinesq Models. Systems 239

[62] for details. We then need to know its real point spectrum. Comparing nonlin-

ear and linearized operators in (5.8) and (5.10), one can ﬁnd two ﬁrst successive

eigenvalues and eigenfunctions:

= 6 with ψ

= g(x),andµ

= 0 with ψ

= g



(x ),

where g(x)>0andg



(x ) has precisely a single zero at x = 0in(−π,π).Usingthe

relation between µ

and λ

, we obtain the following eigenvalues of the pencil:

= 1,λ

= 0,λ

=−5, and λ

=−6. (5.12)

By Sturm’s Theorem, other eigenfunctions (if any) ψ

(x ) with k ≥ 2havek zeros

and must correspond to eigenvalues µ

<µ

= 0. Solving the quadratic equations

+ 5λ

− µ

= 0 yields, for any k ≥ 2, eigenvalues λ

with negative real parts.

It is worth mentioning that the linear ODE (5.11) for µ

< −3 exhibits oscillatory

behavior near the singular endpoint x =±π, so the spectrum of A



[g] is not discrete

and contains a continuous counterpart belonging to the stable half of the complex

plane. Indeed, this makes the linearized problem more difﬁcult, as it includes integral

terms in eigenfunction expansions over the continuous spectrum, which reﬂects the

strong nonlinear degeneracy of the original PDE.

We have detected a single eigenvalue λ

= 1, corresponding to an unstable mode.

It should be excluded from stability analysis, since it corresponds to the shifting

of the blow-up time T (see computation below), which is ﬁxed via rescaling (5.7).

Therefore, g is exponentially asymptotically stable in the linear approximation. For

many sufﬁciently smooth nonlinear evolution PDEs, and especially for parabolic

ones, it is known that linear stability for the linearized equations implies that the

nonlinear stability is true for the full PDE. This is called the principle of linearized

stability; see Lunardi [403, Ch. 9]. For the degenerate quasilinear hyperbolic equa-

tion (5.8), such questions are

OPEN and, bearing in mind complicated spectral prop-

erties of the corresponding quadratic pencil, are difﬁcult to prove.

Linear stability on W

for the DS (5.4). Let us perform blow-up stability analysis

on the subspace W

. There exists a direct sum decomposition of W

into the two 1D

invariant subspaces,

= W

⊕ W

, or W

= W

⊕ W

−

, (5.13)

with clear and simple blow-up behavior on each of them. What kind of stable blow-

up evolution can be detected on the wider subspace W

? For simpler quasilinear

parabolic PDEs, we managed to prove stability of self-similar blow-up evolution

on W

(see Example 3.17). Unlike the parabolic case, for the hyperbolic PDE, the

quadratic DS (5.4) is of fourth order and we cannot perform such a complete global

stability analysis. We again restrict ourselves to a linearized stability study.

For linear stability analysis, we introduce the rescaled blow-up variables

1,2

(t) =

(T −t )

1,2

(τ ), with τ =−ln(T − t) →+∞, (5.14)

and obtain the DS





=−5ϕ



+ 2ϕ

+ ϕ

− 6ϕ



=−5ϕ



+ 3ϕ

− 6ϕ

(5.15)

240 Exact Solutions and Invariant Subspaces

The blow-up solution on W

given by C

(t) = C

(t) = 2(T − t)

corresponds to

the equilibrium (ϕ

,ϕ

) = (2, 2). Linearizing (5.15) about (2, 2) by setting

1,2

= 2 +Y

1,2

yields the linearized system





=−5Y



+ 2Y

+ 4Y



=−5Y



+ 6Y

(5.16)

In variables Z = (Y

, Y



, Y



)

, it is written as the DS



= AZ, with the 4 ×4matrix A =







0100

2 −54 0

0001

600−5







It is not surprisingthat the non-symmetricmatrix A has four real eigenvalues λ

= 1,

=−1, λ

=−4, and λ

=−6, where the ﬁrst and the last one are the same, as

in the point spectrum (5.12) of the quadratic pencil. Hence, (2, 2) is a hyperbolic

equilibrium of the nonlinear system (5.15) and we can apply the Hartman–Grobman

Theorem [460, p. 118] to classify this stationary point. Of course, it is a saddle and

has a 1D unstable manifold which is tangent to the unstable subspace for λ = 1of

the linearized DS.

This unstable manifold should not be taken into account if the blow-up time T is

ﬁxed by scaling (5.14). Indeed, we perform a small change in T , setting T



= T +ε,

to obtain that C

(t) ∼ (T −t)

−2

. In terms of the time-variable τ =−ln(T −t),this

is transformed into



−t)

(T −t)



1 + ε

T −t



−2

(T −t )



1 − 2ε

T −t

+ ...



(T −t )



1 − 2εe

+ ...



(here t ≈ T

−

is ﬁxed and we expand relative to the small parameter ε). Then the

factor

(T −t)

is scaled out by transformation (5.14), so that the remaining term

1 − 2εe

+ ... describes a typical unstable behavior according to the mode with

the eigenvalue λ = 1. Excluding the local 1D unstable manifold yields the following

rescaled stability result.

Proposition 5.2

Let the blow-up time

be ﬁxed in rescaling

(5.14)

. Then, for such

orbits, the equilibrium

(2, 2)

for the DS

(5.15)

is a stable node and, hence, is asymp-

totically stable.

This implies that, in the rescaled sense for the full DS (5.4), the evolution on

subspaces W

is locally asymptotically stable. Thus, any solution on W

being in a

sufﬁcientlysmall neighborhood of W

takes the form (5.6) of the similarity solution

near the blow-up time.

Global analysis of orbits of the fourth-order DS (5.15) is a difﬁcult

OPEN PROB-

LEM. We expect that a certain stability result remains true for the sixth-order DS that

describes blow-up evolution for the hyperbolic PDE (5.2) on the subspace W

L{1, cos x , sin x }.

5 Quasilinear Wave and Boussinesq Models. Systems 241

Example 5.3 (Generalized Boussinesq equation with source) The blow-up dy-

namics (including local stability) do not essentially change if we add some extra lin-

ear terms to thequadratic operator F, leaving W

invariant.For instance, the stability

conclusions remain the same for a generalized Boussinesq equation with source of

the form

=−u

xxxx

+ βu

+ (uu

)

+ γ u

Example 5.4 (Improved Boussinesq equation) Consider a quadratic perturbation

of the improved Boussinesq equation

− αu

ttxx

= βu

+ (uu

)

+ 2u

(α = −1), (5.17)

which admits solutions (5.3), with the DS





= 2C

+ C



1+α

−

1+α

Asymptotic and stability analysis is performed in a similar fashion. The extra linear

term in the second ODE does not affect the asymptotics of blow-up and is scaled out

in stability study.

5.2 Breathers in quasilinear wave equations and blow-up models

Example 5.5 (Breathers) In typical applications, breathers are periodic solutionsof

nonlinear hyperbolic models.

Classical breather. It has been recognized since the 1950s that the integrable sine-

Gordon (sG) equation in 1D

= u

− sin u (5.18)

admits [520] explicit periodic solutions, called breathers (two-soliton solutions)

u(x , t) = 4tan

−1



√

1 − ω

sech



√

1 − ω

x sinωt

 

ω ∈ (0, 1)



In the differential geometry of pseudo-spherical surfaces of constant Gaussian cur-

vature K =−ρ

−2

, the study of (5.18) goes back to Edmond Bour (1862), Bon-

net (1867), and Enneper (1868), [169], and the PDE is sometimes called the En-

neper equation; see historical aspects in [521]. Detailed investigations of various

forms of (5.18), including superposition behavior of its solutions, were performed

by B¨acklund, Bianchi, Darboux and others, and “this work ... was essentially com-

plete by the turn of the century...,” [521, p. 1535]. The name sine-Gordon is asso-

ciated with further exploitation of this equation as a 1D model of meson theory of

nuclear forces developed in the 1960s, when this name has become customary (in

1967, G.L. Lamb used (5.18) for the study of propagation of ultrashort light pulses).

Existence and nonexistence of periodic solutions of the general Klein–Gordon

(KG) equation

= u

− g(u),

242 Exact Solutions and Invariant Subspaces

with an arbitrary nonlinearity g(u) on the right-hand side, is an important problem,

in view of various physical applications in electromagnetizm, nonlinear optics, and

quantum ﬁeld theory. We refer to Segur–Kruskal [522], where an asymptotic ap-

proach to nonexistence of periodic solutions of the φ

model

= u

− 2u + 3u

− u

wasproposed.Existence,nonexistence,and multiplicityof periodic solutions of non-

linear hyperbolic equations is an important direction of general PDE theory. We re-

fer to Mitidieri–Pohozaev [425, Ch. 8], where a large amount of related existence-

nonexistence results and further references are available.

More recent applications of breathers are associated with lattice theory that leads

to discrete models. These models can involve many unit cells on the microscopic

level and occur in the mathematical modeling of many physical processes, from

chemical reaction theory and optics, to biology and acoustics. The discrete sine-

Gordon (dsG) equation (or the Frenkel–Kontorova (FK) model from dislocation the-

ory of plastic deformation in crystals, 1938) is an inﬁnite-dimensional DS



= φ

n+1

− 2φ

+ φ

n−1

− sinφ

, n ∈ Z,

which, unlike its continuum counterpart (5.18), is not integrable, but is known to

admit periodic solutions. In Section 9.5, we present further discussion of lattices and

exact solutions on invariant subspaces for such discrete operators.

Compact breathers and localized blow-up patterns. Various lattices for the sG

and more general KG equationsare widely studiednowadays.Rosenau and Schochet

[500] introduced anharmonic lattices, corresponding to the quasilinear anharmonic

KG equation

+ u = 3(u

)

+ u

≡



)



+ u

. (5.19)

The operator on the right-hand side is variational and is a Frechet derivative of the

following (Lagrangian) potential:

(u) =−



)

dx +



dx for u ∈ W

1,4

(IR ) ∩ L

(IR ).

For us, equation (5.19) has particular interest, since it admits a compact breather

solution in separable variables [500]

(x , t) = ϕ(t) f (x), (5.20)

where these two functions solve the ODEs



= ϕ

− ϕ and 3( f



)



+ f

− f = 0.

The ﬁrst ODE for ϕ(t) admits a periodic solution,while the second equation for f (x)

has a compactly supported weak solution with ﬁnite interfaces yielding the compact

breather. Furthermore, the ODE for ϕ(t) admits blow-up solutions, so (5.20) then

presents localized patterns of regional blow-up (an S-regime).

It is curious that the spatial part f (x) of the compact breather (5.20) is the same

as in blow-up analysis of the quasilinear parabolic p-Laplacian equation

= 3(u

)

+ u

. (5.21)