Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics
Подождите немного. Документ загружается.


4 Korteweg-de Vries and Harry Dym Models 203
50 40 30 20 10 0 10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
y
f(y)
k=1
k=2
Figure 4.18 The first blow-up patterns of (4.154), p = 3, for k = 1andk = 2.
The first blow-up patterns are calculated numerically and are shown in Figure 4.18
for p = 3 in the third, k = 1, and fifth-order, k = 2, cases. Notice the oscillatory tail
as y →−∞,whichfork = 1 corresponds to the Airy function (4.139). The decay
as y →+∞is exponentially fast, non-oscillatory for k = 1, and oscillatory for any
k ≥ 2. Existence and multiplicity of solutions for (4.154)in IR are
OPEN PROBLEMS
and are more difficult in higher-order cases (k ≥ 2). It is curious that blow-up is
not single point. For instance, for k = 1, using expansions in (4.139), we find that,
roughly speaking,
u(x , T
−
) =
0forx > 0,
±∞ for x < 0,
where “±∞” means unbounded oscillatory behavior. Namely, at every fixed point
x
0
< 0, the final-time profile is unboundedfor p < 13 (we expect that such solutions
exist for p > 1 below the bifurcation point p
0
= 4),
u(x , t) ∼ (T − t)
−
1
p−1
x
0
(T −t)
1/3
−
1
4
cos(...) = (T − t)
p−13
12( p−1)
|x
0
|
−
1
4
cos(...).
Example 4.32 (Oscillatory solutions in higher-order mKdV equations) Oscilla-
tory, changing sign solutions at finite interfaces are achieved in higher-order mKdV-
type models, such as the fifth-order one
u
t
+
|u|
−n
u
x
+ u
xxxxx
= 0 (n > 0).
Then TWs satisfy −λf
+ (| f |
−n
f )
+ f
(5)
= 0, so that, close to interfaces,
f
(4)
+|f |
−n
f = 0fory > 0, f (0) = 0,
using representation (4.152) with γ =
4
n
. A periodic oscillatory behavior for ODEs
like (4.153), with P
3
→ P
4
, was studied in Example 4.10.
© 2007 by Taylor & Francis Group, LLC

204 Exact Solutions and Invariant Subspaces
4.5 On compactons in IR
N
for nonlinear dispersion equations
Invariant subspaces for operators in IR
N
will be systematically studied in Chapter
6, including compact moving structures. Here we present a few examples of com-
pactons in IR
N
, whose construction is based on the known 1D analysis. For com-
pactons, this study is continued in Section 6.7. Many problems of existence, unique-
ness, and asymptotics for the PDEs in this section are
OPEN.
Example 4.33 (KP equation with nonlinear dispersion) Consider the PDE
u
t
+ uu
x
+ (u
2
)
xxx
x
+
⊥
u = 0, (4.155)
which is the Kadomtsev–Petviashvili equation in IR
N
×IR with nonlinear dispersion.
Here X = (x, x
) is the spatial variable, with x ∈ IR and x
= (x
2
, ..., x
N
) ∈ IR
N−1
.
The Laplacian
⊥
takes into account the variable x
. This equation in IR
3
× IR was
introduced by Rosenau and Hyman [496, p. 567] to demonstrate multi-dimensional
compactonsof specialand unusualstructure.These are treatedbelowby using invari-
ant subspaces. We continue to call such solutions compactons, though their supports
are not bounded or of finite measure, but their solutions exhibit special types of finite
propagation.
Consider solutions on the trigonometric subspace W
3
= L{1, cosγ x, sinγ x},
u(X, t) = C
1
(x
, t) + C
2
(x
, t) cosγ x + C
3
(x
, t) sin γ x, (4.156)
with a constant γ to be determined.Plugging (4.156) into the PDE (4.155) yields the
following expansion on W
5
= W
3
⊕ L{cos2γ x , sin 2γ x}:
⊥
C
1
+
γ
C
3t
+ γ(2γ
2
− 1)C
1
C
2
+
⊥
C
2
cosγ x
−
γ
C
2t
− γ(2γ
2
− 1)C
1
C
3
+
⊥
C
3
sinγ x
+γ
2
(8γ
2
− 1)
C
2
2
− C
2
3
cos2γ x +2γ
2
(8γ
2
− 1)C
2
C
3
sin2γ x = 0.
The last two terms (projections onto cos2γ x and sin2γ x ) simultaneously vanish if
γ =
1
2
√
2
. (4.157)
Then the restriction of (4.155) to W
3
is a system of three equations for expansion
coefficients {C
1
, C
2
, C
3
},
⊥
C
1
= 0,
C
2t
+
3
8
√
2
C
1
C
3
− 2
√
2
⊥
C
3
= 0,
C
3t
−
3
8
√
2
C
1
C
2
+ 2
√
2
⊥
C
2
= 0.
(4.158)
Hence, C
1
(x
, t) is an arbitrary solution of the Laplace equation in the variable x
,
and the last two PDEs give a linear system for {C
2
, C
3
} that is not studied in detail.
Note though that choosing a constant function C
1
(x
, t) ≡ A yields a linear fourth-
order hyperbolic PDE for C
3
,
C
3tt
+ 8
2
⊥
C
3
−
3A
2
⊥
C
3
+
9A
2
128
C
3
= 0,
which e.g., possesses explicit solutions on simple polynomial subspaces.
© 2007 by Taylor & Francis Group, LLC

4 Korteweg-de Vries and Harry Dym Models 205
We restrict ourselves to self-similar solutions of the system (4.158) by using the
rescaled variables
C
1
=
1
t
U, C
2
=
1
t
V, C
3
=
1
t
W,ξ=
x
√
t
,τ= lnt. (4.159)
Then (4.158) reduces to
V
τ
−
1
2
∇
ξ
V · ξ − V +
3
8
√
2
UW − 2
√
2
ξ
W = 0,
W
τ
−
1
2
∇
ξ
W · ξ − W −
3
8
√
2
UV + 2
√
2
ξ
V = 0,
(4.160)
with an arbitrary function U = U(ξ) satisfying Laplace’s equation. Taking again the
constant function U = A, and looking for solutions as radial TWs,
V = f (s) and W = g(s), where s =
1
2
|ξ|
2
− λτ, (4.161)
where λ>0 is a constant, gives the following system for {f, g}:
λf
+
1
2
f
|ξ|
2
+ f −
3
8
√
2
Ag + 2
√
2
g
|ξ|
2
+ (N − 1)g
= 0,
λg
+
1
2
g
|ξ|
2
+ g +
3
8
√
2
Af − 2
√
2
f
|ξ|
2
+ (N − 1) f
= 0.
(4.162)
Projecting equations of (4.162) onto |ξ|
2
and 1, we obtain two standard systems
1
2
f
+ 2
√
2 g
= 0,
1
2
g
− 2
√
2 f
= 0,
λf
+ f −
3
8
√
2
Ag + 2
√
2(N − 1)g
= 0,
λg
+ g +
3
8
√
2
Af − 2
√
2(N − 1) f
= 0.
(4.163)
The first system yields a single ODE for f , f
+
1
32
f
= 0, which results in
f (s) = B cos(as) and g(s) = C sin(as), where a =
1
4
√
2
, (4.164)
and B, C ∈ IR . Substituting these functions into the second system in (4.163) and
projecting each equation onto cosas and sinas yields two linear algebraic equalities
B + 2
√
2(N − 1)Ca = 0,
λBa +
3
8
√
2
AC = 0,
λCa +
3
8
√
2
AB = 0,
C + 2
√
2(N − 1)Ba = 0.
(4.165)
From the first system, we find A =
1
3
(N − 1)λ and C =−
2
N−1
B. Substituting into
the second equation of the second system yields
−
2
N−1
+
N−1
2
= 0 ⇒ (N −1)
2
= 4, i.e., N = 3.
Then the first equation implies C =−B. Notice that there is another formal hypo-
thetical dimension N =−1 corresponding to the “unstable” radial Laplacian
r
= r
2
D
r
1
r
2
D
r
≡ D
2
r
−
2
r
D
r
,
which occurs in some problems of plasma physics.
Thus, the overdetermined system (4.162) is consistent in the 3D geometry only,
N = 3, and the solution is
C
1
= A =
2λ
3
, f (s) = B cos
s
4
√
2
, and g(s) =−B sin
s
4
√
2
, (4.166)
where B ∈ IR is arbitrary. Substituting into (4.156) gives solutions on W
3
,
u(X, t) =
2λ
3t
+
B
t
cos
γ x +
γ
2
1
2t
|x
|
2
− λ ln t
.
© 2007 by Taylor & Francis Group, LLC
206 Exact Solutions and Invariant Subspaces
The compacton is achieved at B =
2λ
3
and takes the form
u
c
(X, t) =
4λ
3t
cos
2
1
4
√
2
x +
1
4t
|x
|
2
−
λ
2
lnt
, (4.167)
where u
c
= 0 if the absolute value of the argument of cos is larger than
π
2
.
In order to illustrate this type of finite propagation for the compacton (4.167),
consider the corresponding linear PDE (for simplicity, with x
= y ∈ IR )
u
tx
+ u
yy
= 0inIR
2
× IR
+
. (4.168)
In particular, let us study its similarity solutions
u(x , y, t) =
1
√
1+t
f (x,η), η =
y
√
1+t
⇒ f
ηη
=
1
2
( f
x
η)
η
.
This PDE is easily integrated (the fundamentalsolution belongs to the same family).
For instance, there are solutions
u(x , y, t) =
1
√
1+t
ψ
x +
1
4(1+t )
y
2
, (4.169)
where ψ(s) is an arbitrary C
∞
function supported on the interval [−1, 1]. Solu-
tion (4.169) has the support localized between two paraboloids; cf. (4.167). In other
words,linear equation(4.168) supports this kind of finite propagation,and such typi-
cal supportshapes are reflected by the nonlinear PDE (4.155). As in Example 4.8, we
can use the TWs to check that such compactonsare solutions of the Cauchy problem
and do not need an FBP setting.
Example 4.34 (Sixth-order PDE with nonlinear dispersion) For higher-order ex-
tensions, we will use our 1D analysis in Example 4.5. Consider the sixth-order PDE
composed in a similar manner,
[u
t
− α(u
2
)
xxxxx
− β(u
2
)
xxx
− γ(u
2
)
x
]
x
+
⊥
u = 0 (4.170)
in IR
N
× IR . The quadratic fifth-order operator admits W
3
= L{1, cos x , sin x} if
16α − 4β + γ = 0, and there exist solutions
u(X, t) = C
1
(x
, t) + C
2
(x
, t) cos x +C
3
(x
, t) sin x. (4.171)
Substituting into (4.170) yields a similar system (here µ = 6(β − 5α))
⊥
C
1
= 0,
C
2t
− µ C
1
C
3
−
⊥
C
3
= 0,
C
3t
+ µ C
1
C
2
+
⊥
C
2
= 0.
(4.172)
There exist similarity solutions (4.159), (4.161). For N = 3, the explicit solutions
are given, instead of (4.166), by
C
1
= A =−
λ
2µ
, f (s) = B cos
s
2
, and g(s) =−B sin
s
2
.
The compacton solution takes place for B = A =−
λ
2µ
,
u
c
(X, t) =−
λ
µt
cos
2
1
2
x +
1
4t
|x
|
2
−
λ
2
lnt
. (4.173)
Its support is unbounded and lies between two paraboloids in IR
3
,
suppu
c
(X, t) =
4t
λ
2
lnt −π − x
≤|x
|
2
≤ 4t
λ
2
lnt + π − x
.
© 2007 by Taylor & Francis Group, LLC
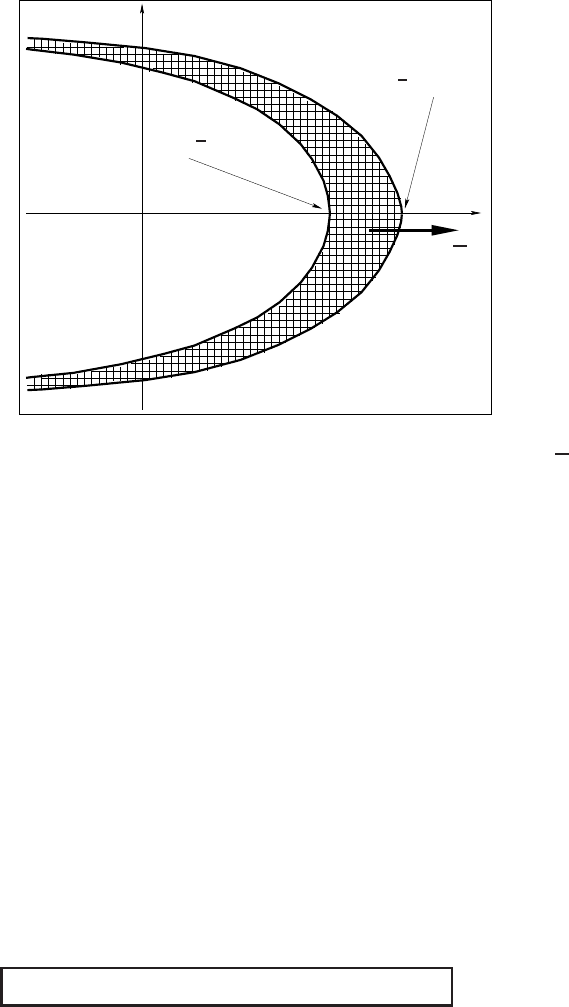
4 Korteweg-de Vries and Harry Dym Models 207
v =
λ
2t
x =
λ
2
lnt −π
x =
λ
2
lnt +π
x
x
0
Figure 4.19 The support of compacton (4.173) moves to the right with the speed v =
λ
2t
.
This is shown in Figure 4.19, where, for convenience,we treat x
as a single variable.
As in Example 4.8, we show that C
1
-compactons(4.173) are not sufficiently smooth
at {u = 0} to satisfy the Cauchy problem, and need a standard FBP zero contact
angle setting. In order to obtain C
3
-compactons, as in (4.105), we need a PDE with
the operator (4.103) for which manipulationswith the expansion coefficientsinclude
five PDEs in the resulting difficult system, such as (4.172).
Example 4.35 (Zakharov–Kuznetsov PDE with nonlinear dispersion)Inplasma
physics, in the presence of strong magnetic fields, the evolution of the ion density in
a strongly magnetized ion-acoustic plasma is described by the Zakharov–Kuznetsov
(ZaK) equation [591]
u
t
+ uu
x
+ u
xxx
+ u
xyy
= 0inIR
2
× IR , (4.174)
where a magnetic field is directed along the x-axis. This, together with the KP equa-
tion, is one of the best known 2D generalization of the KdV equation that describes
two-dimensional modulations of solitons. Note that the KP equation is limited by
the assumption of weak two-dimensionality; see details and references in [527]. But,
unlike the KP equation, (4.174) is not integrable by the inverse scattering transform
method.
Consider the higher-order ZaK-type equation with nonlinear dispersion,
u
t
−
α(u
2
)
xxxxx
+ β(u
2
)
xxx
+ γ(u
2
)
x
+
⊥
u
x
= 0 (4.175)
in IR
N
× IR , and study it on W
3
= L{1, cos x , sin x} in the case where
16α − 4β + γ = 0.
© 2007 by Taylor & Francis Group, LLC
208 Exact Solutions and Invariant Subspaces
The correspondingsolutions have the same form as (4.171) and are driven by the DS
(4.172), where the first equation is replaced by the stationary one,
C
1t
= 0.
Taking the constant function C
1
(x
, t) ≡ A gives the linear system
C
2t
− ρ C
3
+
⊥
C
3
= 0,
C
3t
+ ρ C
2
−
⊥
C
2
= 0,
where ρ = µA = 6(β − 5α)A. This is reduced to a linear fourth-order hyperbolic
equation,
C
3tt
=−
2
⊥
C
3
+ 2ρ
⊥
C
3
− ρ
2
C
3
.
In particular, for N = 2, denoting x
= y yields the solution
C
3
(y, t) = B sin[κ(y − λt)],
where κ>0 depends on the TW speed λ = 0 as follows: κ
2
− κλ + ρ = 0.
Determining a similar coefficient C
2
(y, t),wefind the solution
u(x , y, t) = A + B cos[κ(y − λt) − x],
where setting A = B yields the TW compacton
u
c
(x , y, t) = 2A cos
2
[
1
2
(κy − x − κλt)].
Its support is a moving strip in the {x, y}-plane,
|κy − x − κλt|≤π.
Forthe third-orderPDE (4.175) with α = 0, such a compacton seems to be a solution
of the Cauchy problem by the same reasons detailed in Example 4.33, while, for the
fifth-order case with α = 0, a standard FBP setting is necessary to support it.
Example 4.36 (N = 2) Let us nowdemonstrateslightlydifferenttypeof compacton
solutions for quadratic PDEs. Without loss of generality, consider the simplest KP-
type equation
u
t
− (uu
xx
)
x
− (u
2
)
x
x
+
⊥
u = 0inIR
N
× IR
+
. (4.176)
Manipulations remain the same and lead to similar systems also for the fifth-order
operators introduced above. Since the quadratic operator in (4.176) admits subspace
W
3
, looking for solutions (4.171) yields the PDE system (4.172) with µ = 1. We
now do not use the similarity scaling, as in (4.159), and set
C
1
=
1
√
t
U, C
2
=
1
√
t
V, C
3
=
1
√
t
W,ξ=
1
√
t
x
,τ= lnt,
to get a non-autonomousPDE system,
V
τ
−
1
2
∇
ξ
V · ξ −
1
2
V − e
τ
2
UW −
⊥
W = 0,
W
τ
−
1
2
∇
ξ
W · ξ −
1
2
W + e
τ
2
UV +
⊥
V = 0,
where, as usual, U = A. Looking for solutions (4.161) with
s =
1
2
|ξ|
2
− λe
τ
2
,
© 2007 by Taylor & Francis Group, LLC

4 Korteweg-de Vries and Harry Dym Models 209
we obtain the following ODE system:
f
(−
λ
2
)e
τ
2
−
1
2
f
|ξ|
2
−
1
2
f −e
τ
2
Ag −
g
|ξ|
2
+ (N −1)g
= 0,
g
(−
λ
2
)e
τ
2
−
1
2
g
|ξ|
2
−
1
2
g + e
τ
2
Af +
f
|ξ|
2
+ (N −1) f
= 0.
(4.177)
Unlike in all the previous examples, this consists of three independent systems as
“projections” onto e
τ
2
, |ξ|
2
, and 1:
λ
2
f
+ Ag = 0,
−
λ
2
g
+ Af = 0,
1
2
f
+ g
= 0,
−
1
2
g
+ f
= 0,
−
1
2
f −(N −1)g
= 0,
−
1
2
g
+ (N −1) f
= 0.
From the second system, f
+
1
4
f
= 0, so that (4.164) holds with a =
1
2
.Thefirst
system yields A =−
λ
4
and C
2
= B
2
,i.e.,C =±B. Taking as usual C =−B and
substituting into the third one, one obtains
−
1
2
+
N−1
2
= 0 ⇒ N = 2.
Similarly, for C = B we get −
1
2
−
N−1
2
= 0, i.e., another hypothetical dimension
N = 0 for which the radial Laplacian is (again appears in plasma physics)
r
= rD
r
1
r
D
r
≡ D
2
r
−
1
r
D
r
.
Finally, the system (4.177) is consistent for N = 2 only with the solution
U = A =−
λ
4
, f (s) = B cos
s
2
, and g(s) =−B sin
s
2
.
This yields a family of solutions of equation (4.176),
u(X, t) =
1
√
t
−
λ
4
+ B cos
x +
1
4t
|x
|
2
−
λ
2
√
t
,
where B is arbitrary. Setting B =−
λ
4
leads to the compacton
u
c
(X, t) =−
λ
2
√
t
cos
2
1
2
x +
1
4t
|x
|
2
−
λ
2
√
t
≥ 0forλ<0, (4.178)
where, as usual, we set u
c
= 0 for arguments of cos
2
, |
1
2
(·)|≥
π
2
. The regularity
of u
c
is sufficient to satisfy the Cauchy problem for equation (4.176). For higher-
order PDEs of the type (4.170), such C
1
-compactons u
c
need an FBP setting. The
C
3
compactons as in (4.105)demand 5D subspaces for which the explicit integration
of the corresponding PDE systems is unknown.
Example 4.37 (Cubic PDE) Consider a cubic PDE of the KP-type (cf. (4.155))
u
t
− (u(u
2
)
xx
)
x
− 4(u
3
)
x
x
+ u
yy
= 0inIR
2
× IR
+
, (4.179)
where the operator is chosen to admit W
2
= L{cosx, sin x}.OnW
2
,i.e.,for
u(x , y, t) = C
1
(y, t) cos x + C
2
(y, t) sin x,
equation (4.179) reduces to the PDE system in IR × IR
+
,
C
1t
− 2C
2
C
2
1
+ C
2
2
− C
2yy
= 0,
C
2t
+ 2C
1
C
2
1
+ C
2
2
+ C
1yy
= 0.
(4.180)
In an analogous way, looking for similarity solutions of (4.180) in the form of
C
1
=
1
√
t
f (s), C
2
=
1
√
t
g(s), where s =
1
4t
y
2
+ λτ and τ = lnt,
© 2007 by Taylor & Francis Group, LLC

210 Exact Solutions and Invariant Subspaces
yields the compacton solution for λ<0, with interfaces as moving parabolas,
u
c
(x , y, t) =
−
λ
2t
cos
x +
1
4t
y
2
− λ ln t
,
where u
c
= 0in{|x +
1
4t
y
2
−λ ln t|≥
π
2
}. Comparing with the TWs shows that this
Lipschitz continuous function can be a solution of the Cauchy problem.
4.6 “Tautological” equations and peakons
4.6.1 Trigonometric subspaces
We next consider another class of third and higher odd-order PDEs.
Example 4.38 (Rosenau equation) Consider the quasilinear degenerate Rosenau
equation [491]
u
t
+ u
xxt
= 3uu
x
+
uu
xx
+
1
2
(u
x
)
2
x
≡ F
3
[u]inIR × IR ; (4.181)
see references, applications, and results in [449] and Remarks. We begin with some
evolution aspects of the dynamics on the invariant subspace for a more general PDE
with two parameters
u
t
+ u
xxt
= 3uu
x
+ αuu
xxx
+ βu
x
u
xx
≡ F[u]inIR × IR . (4.182)
In (4.181), α = 1andβ = 2. This family was also introduced in [491].
Proposition 4.39
Operator
F
in
(4.182)
admits
W
3
= L{1, cosγ x, sinγ x}
if
γ
2
=
3
α+β
> 0. (4.183)
As usual, for the opposite sign in (4.183), the subspaces of exponential or hyper-
bolic functions are used. Describing the dynamics on W
3
, and assuming that (4.183)
holds, we obtain for (4.182) solutions
u(x , t) = C
1
(t) + C
2
(t) cosγ x +C
3
(t) sin γ x,
C
1
= 0,
(1 − γ
2
)C
2
= (3γ − αγ
3
)C
1
C
3
,
(1 − γ
2
)C
3
=−(3γ − αγ
3
)C
1
C
2
.
There exist three different cases:
Case 1: γ
2
= 1. Denoting
ρ =
γ(αγ
2
−3)
1−γ
2
and integrating the DS yields
u(x , t) = A + B cos(x − ρ At)(A, B ∈ IR ).
Setting A = B and ρ A = λ determines the compacton solution
u
c
(x , t) =
2λ
ρ
cos
2
[
1
2
(x − λt)], (4.184)
that is localized in the support |x −λt|≤π movingwith constant speed. The analogy
© 2007 by Taylor & Francis Group, LLC

4 Korteweg-de Vries and Harry Dym Models 211
with the results in Example 4.8 suggests that these compactons are solutions of the
Cauchy problem.
Case 2: γ
2
= 1. Hence,
α + β = 3,
and if α = 3 (this is true for (4.181)), then the DS takes a simpler form C
1
= 0,
C
1
C
3
= C
1
C
2
= 0. Therefore, C
1
(t) ≡ 0, so we can choose arbitrary functions
C
2
(t) and C
3
(t) to obtain the following dynamics on such invariant subspaces.
Proposition 4.40
For any
α ∈ IR
, the equation
u
t
+ u
xxt
= 3uu
x
+ αuu
xxx
+ (3 − α)u
x
u
xx
≡ F
α
[u] (4.185)
holds true on the subspace
W
2
= L{cos x, sin x}
that is invariant under
F
α
.
The result is obvious if (4.185) is written in the form
(u + u
xx
)
t
= αu(u + u
xx
)
x
+ (3 − α)u
x
(u + u
xx
).
Observe that the linear operator
L = I +
d
2
dx
2
(4.186)
is the annihilating operator of the subspace W
2
, i.e., L : W
2
→{0}. We call
such PDEs, whose right and left-hand sides are composed of annihilating opera-
tors of a given subspace, the tautological equations (on prescribed subspaces). As
far as evolution properties are concerned, this implies that (4.185) admits an infinite-
dimensional set of 2π-periodic solutions
u(x , t) = C
2
(t) cos x + C
3
(t) sin x , (4.187)
where C
2,3
(t) are arbitrary C
1
-smooth functions. So, given initial data
u
0
(x ) = a cosx + b sin x ∈ W
2
,
the Cauchy problem, or the 2π-periodic initial-boundary value problem, for (4.185)
has an infinite-dimensional set of smooth solutions (4.187), where C
2
(0) = a and
C
3
(0) = b. Therefore, the equation on W
2
(or in some neighborhood of W
2
) is not a
well-posed evolution PDE in the space of bounded periodic functions.
Let us next consider non-smooth solutionson W
2
, which, possibly, make sense for
such third-order PDEs. For instance, consider the following traveling wave solution:
u
1
(x , t) = λ sin |x − λt|,
where λ ∈ IR is the speed of propagationof the weak shock wave at x = λt being the
point of discontinuity of the derivative u
x
. Extending u
1
(x , t) from {|x − λt|≤π}
symmetrically yields a π -periodic structure. More general π-periodic solutions of
this type have the form
u
N
(x , t) =
N
i=1
p
i
(t) sin |x −q
i
(t)|,
where {p
i
, q
i
} are smooth functions still remaining arbitrary.
According to PDE theory, evolution properties of such solutions (periodic mul-
tipeakons; see further interpretations below) should be checked in the π-periodic
© 2007 by Taylor & Francis Group, LLC

212 Exact Solutions and Invariant Subspaces
setting in the domain (−
π
2
,
π
2
) × IR with periodic boundary conditions by using the
integral form of the PDE. Writing (4.181) as
L[u
t
] = L[uu
x
] +
u
2
−
1
2
(u
x
)
2
x
and applying L
−1
with the kernel
ω(s) =
1
2
sin|s| in
−
π
2
,
π
2
,
we formally obtain the integro-differential equation
u
t
= uu
x
+
ω ∗
u
2
−
1
2
(u
x
)
2
x
. (4.188)
Integration by parts, which is used for deriving (4.188), assumes certain “regularity”
of solutions. This includes Rankine–Hugoniot,as well as some other “entropy-type”,
conditions at weak shocks. It would be interesting (an
OPEN PROBLEM) to detect if
such solutions can be obtained via a fourth-order parabolic regularization,
u
t
+ u
xxt
= F[u] − εu
xxxx
(ε > 0), (4.189)
by passing to the limit ε → 0. What if the sixth-order regularization ... + εu
xxxxxx
on the right-hand side of (4.189) applies?
Evolutionpropertiesof singularities of periodicmultipeakonsfor (4.188)or (4.189)
were less well studied in the literature. Another famous model with true multi-
peakons is considered in the next subsection.
Case 3: α = 3. Then, if β = 0, the DS reduces to C
1
= 0, so the general solution of
(4.182) is
u(x , t) = A + C
2
(t) cos x + C
3
(t) sin x ,
with arbitrary functions C
2,3
(t) and any constant A ∈ IR .
Example 4.41 (Tautological PDEs) Using the annihilating operator (4.186), it is
easy to construct many equations that are tautological on W
2
. For instance, any fully
nonlinear equations
(i)
a
i
(u, u
x
, ...)D
i
t
L[u] =
( j )
b
j
(u, u
x
, ...)D
j
x
L[u],
with arbitrary coefficients {a
i
(·)} and {b
j
(·)}, are tautological. In particular, the fol-
lowing fourth-order PDE:
u
t
+ u
xxt
= 3uu
x
+ uu
xxx
+ 2u
x
u
xx
+ (I + D
2
x
)[|u|(u + u
xx
)] (4.190)
is tautological on W
2
. In view of the analysis of higher-order degenerate TFEs (Ex-
ample 3.10) and KdV equations (Example 4.8), correct evolution setting of com-
pactly supported solutions is difficult to justify. For instance, in the integral repre-
sentation for (4.190) via convolution with the kernel ω, we obtain the degenerate
parabolic PDE (here it remains parabolic in {u < 0})
u
t
=|u|u
xx
+|u|u + uu
x
+
ω ∗
u
2
−
1
2
(u
x
)
2
x
, (4.191)
containingan extra non-local (compact) perturbation.Such parabolic PDEs naturally
admit solutions that are non-smoothat the singularity level {u = 0}, though standard
© 2007 by Taylor & Francis Group, LLC
