Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics
Подождите немного. Документ загружается.

4 Korteweg-de Vries and Harry Dym Models 193
0 20 40 60 80 100
0.1
0.08
0.06
0.04
0.02
0
0.02
0.04
0.06
0.08
0.1
η
Φ(η)
(a) n = 0.5
0 50 100 150 200
1
0.8
0.6
0.4
0.2
0
0.2
0.4
0.6
0.8
1
x 10
4
η
Φ(η)
(b) n = 0.1
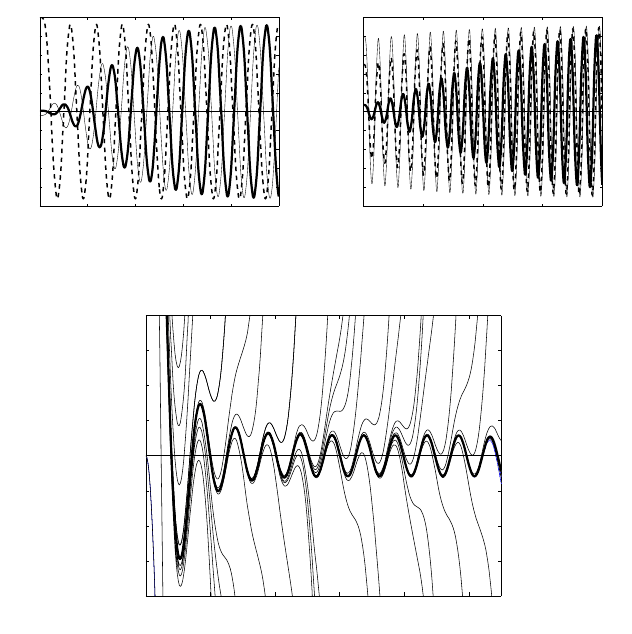
Figure 4.16 Periodic behavior for (4.116), λ = 1, n = 0.5(a),andn = 0.1(b).
0 2 4 6 8 10
2
1.5
1
0.5
0
0.5
1
1.5
2
x 10
5
s
F(s)
Figure 4.17 Unstable periodic behavior of the ODE (4.114), λ =−1, for n = 15. Cauchy
data are F(0) = 10
−4
, F
(0) = F
(0) = 0, F
(0) =−5.0680839826093907... × 10
−4
.
Proposition 4.18
Operator
(4.117)
admits
W
3
= L{1, cosx, sin x}
iff
β = 13
and
γ = 36
.
Hence, the PDE
u
t
= D
5
x
(u
3
) + 13(u
3
)
xxx
+ 36(u
3
)
x
(4.118)
admits exact solutions (4.18) with the DS
C
1
= 0,
C
2
= 18
4C
2
1
+ C
2
2
+ C
2
3
C
3
,
C
3
=−18
4C
2
1
+ C
2
2
+ C
2
3
C
2
.
There exist two first integrals
C
1
= A and C
2
2
+ C
2
3
= B.
Then the DS provides us with explicit TW solutions
u(x , t) = D
1
+ D
2
cos(x −λt) + D
3
sin(x − λt),
© 2007 by Taylor & Francis Group, LLC

194 Exact Solutions and Invariant Subspaces
where D
k
are arbitrary constants and
λ =−18
4D
2
1
+ D
2
2
+ D
2
3
< 0.
Choosing D
3
= 0andD
1
= D
2
yields the compacton (obtained in [147] by a
different approach)
u
c
(x , t) =
−
2λ
45
cos
2
[
1
2
(x −λt)]for|x −λt| <π. (4.119)
According to the maximal regularity of the TW profiles satisfying
−λ f = ( f
3
)
(4)
for y > 0, f (0) = 0,
we see that, for any uniformly bounded oscillatory component ϕ(s),
f (y) = y
2
ϕ(ln y) = O(y
2
) as y → 0.
Since (4.119) exhibits precisely this maximal regularity at the interfaces, it can be
considered as a solution of the Cauchy problem for (4.118). As usual, this does not
mean positivity-likefeatures of general solutionsof (4.118).The function F = ϕ
3
(s)
satisfies the ODE (4.93) with n = 2(i.e.,µ = 6), so that the generic behavior is
oscillatory for λ>0 and is described by a stable periodic orbit ϕ(s).
Example 4.19 (Fifth-degree operators) Consider operators of the algebraic ho-
mogenuity five,
F[u] = D
5
x
(u
5
) + β(u
5
)
xxx
+ γ(u
5
)
x
. (4.120)
Proposition 4.20 (i)
Operator
(4.120)
admits
W
2
= L{cos x , sin x}
iff
β = 34
,
γ = 225
;and
(ii)
does not preserve
W
3
= L{1, cos x , sin x}
.
In (ii), the invariance condition consists of fourteen nonlinear algebraic equations
for β and γ which are not consistent. The corresponding PDE on W
2
,
u
t
= D
5
x
(u
5
) + 34(u
5
)
xxx
+ 225(u
5
)
x
, (4.121)
possesses solutions
u(x , t) = C
1
(t) cos x + C
2
(t) sin x ,
C
1
= 120
C
2
1
+ C
2
2
2
C
2
,
C
2
=−120
C
2
1
+ C
2
2
2
C
1
.
Using the first integral
C
2
1
+ C
2
2
= A,
this leads to the TW solutions
u(x , t) = D
1
cos(x − λt) + D
2
sin(x − λt)
that depend on two arbitrary constants D
1,2
, with
λ =−120
D
2
1
+ D
2
2
2
< 0.
© 2007 by Taylor & Francis Group, LLC

4 Korteweg-de Vries and Harry Dym Models 195
Setting D
2
= 0 gives a formal compacton (cf. [147])
u
c
(x , t) =
−
λ
120
1
4
cos(x − λt) for |x − λt|≤
π
2
,
0for|x − λt| >
π
2
.
(4.122)
It is curious that this simple Lipschitz continuous function is a solution of the max-
imal regularity and satisfies the Cauchy problem. Using TWs for the leading-order
operator in (4.121), we have the ODE
−λ f = ( f
5
)
(4)
for y > 0, f (0) = 0, (4.123)
which has a linear envelope,
f (y) = y ϕ(s), s = ln y. (4.124)
The oscillatory component ϕ(s) is obtained from the fourth-order ODE (4.93) with
n = 4(µ = 5). In general, solutions are oscillatory near interfaces. Hence, by
(4.124), the Lipschitz continuity of solution (4.122) is the best regularity provided
by the equation (4.123).
Example 4.21 (Q(2, 2, 2)-family) We now analyze a couple of operators from the
family Q(2, 2, 2) of equations (4.17) and study the corresponding PDEs on
W
3
= L{1, cos x , sin x}.
First, it is easy to see that the third-order operator
F
3
[u] =
u(u
2
)
xx
x
+ β(u
3
)
x
does not admit W
3
(but it does W
2
= L{cos x , sin x} for β = 4). Consider next the
fifth-order cubic operator
F
5
[u] =
u(u
2
)
xxxx
x
+ β
u(u
2
)
xx
x
+ γ(u
3
)
x
. (4.125)
Proposition 4.22 (i)
Operator
(4.125)
admits
W
3
iff
β = 5
and
γ = 4
,and
(ii)
does not admit
W
5
given in
(4.102)
.
The corresponding evolution PDE
u
t
=
u(u
2
)
xxxx
x
+ 5
u(u
2
)
xx
x
+ 4(u
3
)
x
possesses exact solutions (4.18), with the DS
C
1
= 0,
C
2
= 2
2C
2
1
+ C
2
2
+ C
2
3
C
3
,
C
3
=−2
2C
2
1
+ C
2
2
+ C
2
3
C
2
.
It follows that C
1
= A and C
2
2
+ C
2
3
= B, and the general solution is given by the
TWs
u(x , t) = D
1
+ D
2
cos(x −λt) + D
3
sin(x − λt),
where D
1,2,3
= constant, and
λ =−2
2D
2
1
+ D
2
2
+ D
2
3
< 0.
© 2007 by Taylor & Francis Group, LLC

196 Exact Solutions and Invariant Subspaces
The compacton is obtained for D
3
= 0andD
1
= D
2
,
u
c
(x , t) =
−
2λ
3
cos
2
[
1
2
(x − λt)]for|x − λt|≤π. (4.126)
By checking the maximal regularity of TWs via the leading term of the PDE, we
obtain, on integration
−λ = ( f
2
)
(4)
for y > 0, f (0) = 0.
The similarity structure of multiple zeros at y = 0isthengivenby
f (y) = y
2
ϕ(s), where s = ln y, (4.127)
and this confirms that the non-oscillatory (λ<0) compacton (4.126), exhibiting the
same regularity at the interfaces, solves the Cauchy problem. As usual, the generic
structure of multiple zeros for λ>0 at interfaces depends on the behavior of the
oscillatory component ϕ(s) for s = ln y &−1. Numerically, we did not see reliable
periodic oscillations. For the signed Q(2, 2, 2) equation,
u
t
= [u(|u|u)
xxxx
]
x
⇒ −λ = (| f | f )
(4)
,
oscillatory solutions (4.127) do exist (see Example 4.10).
4.3.6 Exponential subspaces
For odd-orderPDEs (4.97), dealing with exponential subspaces is easier.
Proposition 4.23
The quadratic operator with constant coefficients
F[u] =
(i≥0)
α
i
D
i
x
(u
2
) (4.128)
preserves the following subspaces:
W
2
= L{1, e
x
},
if
2
i
α
i
= 0; (4.129)
W
3
= L{1, e
x
, e
−x
},
if
2
i
α
i
= 0
and
(−2)
i
α
i
= 0. (4.130)
The result is straightforward by taking
u = C
1
+ C
2
e
x
+ C
3
e
−x
(4.131)
(C
3
= 0 for the subspace in (4.129)) and differentiating the equality
u
2
= C
2
1
+ 2C
2
C
3
+ 2C
1
C
2
e
x
+ 2C
1
C
3
e
−x
+ C
2
2
e
2x
+ C
2
3
e
−2x
.
Example 4.24 Equation (4.97), where
16α + 4β + γ = 0
(two conditions in (4.130) coincide for all odd or even derivatives) admits solutions
(4.131) with an easily derived DS for the expansion coefficients.
The order of the operator (4.128) can be arbitrary, so infinite-order equations can
be considered. Such PDEs are well known in the mathematical literature; see Dubin-
skii [156].
© 2007 by Taylor & Francis Group, LLC

4 Korteweg-de Vries and Harry Dym Models 197
Example 4.25 (“Hyperbolic” PDE of infinite order) Consider the PDE,
u
tt
= sin(αD
x
)u
2
+ u − 1,
where α is a constant, and the linear operator sin(αD
x
) on the right-hand side is
formally defined by
sin(αD
x
) =
(i≥0)
(−1)
i
(2i+1)!
(αD
x
)
2i+1
.
Looking for solutions on W
2
with
u(x , t) = C
1
(t) + C
2
(t)e
x
, (4.132)
the invariance condition (4.129) reads
sin2α = 0,
so we take α =
π
2
. Then, substituting into the equation yields
C
1
+ C
2
e
x
= 2C
1
C
2
(−1)
i
(2i+1)!
π
2
2i+1
e
x
+ C
1
(t) + C
2
(t)e
x
− 1,
and, since the sum in square brackets equals sin
π
2
= 1, this gives the DS
C
1
= C
1
− 1,
C
2
= 2C
1
C
2
+ C
2
.
Then C
1
(t) = 1 + A cosht and C
2
solves a hyperbolic Mathieu equation,
C
2
− (3 + 2A cosht)C
2
= 0.
Example 4.26 (“Reaction-diffusion” equation of infinite order)ThePDE
u
t
= sin(αD
x
)u
2
+ βu
2
,
where |β|≤1, admits solutions (4.132) if
sin2α +β = 0.
4.4 Compactons and interfaces for singular mKdV-type equations
4.4.1 Preliminaries: Airy function, integral equation, and smooth solutions
Example 4.27 (FBP-compactons for mKdV-type equations) We now study some
compacton-like solutions that are not associated with invariantsubspaces or sets, but
are simple and important for a general understanding of FBPs, the Cauchy problem,
and finite propagation.Consider the mKdV-type PDE
u
t
+ u
m
u
x
+ u
xxx
= 0, with parameter m ≥ 0, (4.133)
which at this time is formulated for nonnegative solutions. For m = 1, (4.133) is
the KdV equation, and m = 2 yields the modified KdV (mKdV) equation.Form =
1
2
, (4.133) describes ion-acoustic waves in a cold-ion plasma with non-isothermal
electrons,[517];see Remarks for further applications and references.For such PDEs,
© 2007 by Taylor & Francis Group, LLC

198 Exact Solutions and Invariant Subspaces
basic computations are simple and sometimes explicit. To be precise, looking for
standard TWs
u(x , t) = f (y), with y = x − λt,λ>0, (4.134)
yields the ODE
−λf
+ f
m
f
+ f
= 0 ( f ≥ 0),
so, on integration two times, bearing in mind the compacton with f
= 0at f = 0,
( f
)
2
= Af + λ f
2
−
2
(m+1)(m+2)
f
m+2
, (4.135)
where A > 0 is an arbitrary constant. In this case, for any m > 0, there exists a
periodic solution f (y). In particular, for m = 2, choosing A =
1
3
√
2λ
3/2
yields the
case of explicit integration (see [360] and [494])
u(x , t) =
2
3
√
2λ
cos
2
[
1
2
√
λ(x−λt )]
1−
2
3
cos
2
[
1
2
√
λ(x−λt )]
.
Setting u = 0for
1
2
√
λ|x − λt|≥
π
2
, one obtains a (formal) compacton-like solu-
tion, which is localized in the interval of length 2π/
√
λ. This and similar solutions
given by the ODE (4.135) for any m ≥ 0 are solutions of the FBP, so zero contact
angle free-boundary conditions (4.44) are necessary to support such a compacton
evolution. The dynamic interface equation is determined as in Example 4.8.
Let us present a further comment on this important issue to be dealt with later on:
Such compacton-like solutions of semilinear PDEs with a regular lower-order non-
linear term u
m
u
x
for m > 0 are not solutions of the Cauchy problem. The equation
(4.133) in IR × IR
+
describes processes with infinite propagation. To see this, set
m = 0 (then the above compacton persists to exist if λ<1) and consider the linear
equation
u
t
+ u
xxx
= 0inIR × IR
+
, (4.136)
where the convection term u
x
is eliminated by using the moving frame x → x − t.
For initial data u
0
(x ) with exponential decay at infinity, the unique solution of the
Cauchy problem for (4.136) is given by the convolution
u(x , t) = b(·, t) ∗ u
0
, (4.137)
where b(x , t) is the fundamental solution of the operator
∂
∂t
+ D
3
x
,
b(x, t) = t
−
1
3
g(ξ), ξ =
x
t
1/3
, (4.138)
and g satisfying
g = 1 solves the linear ODE
g
−
1
3
(gξ)
= 0 ⇒ g
−
1
3
gξ = 0.
The unique solution g is given by the Airy function Ai(ξ) and has the following
behavior (see [4, p. 363] for details; recall the reflection x → −x for PDE (4.66)):
g(ξ) ∼
ξ
−
1
4
e
−a
0
ξ
3/2
as ξ →+∞,
|ξ|
−
1
4
cos
a
0
|ξ|
3
2
+ A
as ξ →−∞,
(4.139)
where a
0
=
2
9
√
3andA is a constant. Then (4.137) means that, for any compactly
© 2007 by Taylor & Francis Group, LLC

4 Korteweg-de Vries and Harry Dym Models 199
supported data u
0
(x ) ≡ 0, the solution u(x , t) is not compactly supported for arbi-
trarily small t > 0.
Similarly, (4.137)implies that PDEs, such as (4.133) in IR × IR
+
with the regular
nonlinear term for m ≥ 0, cannot admit nontrivial compactly supported solutions
of the Cauchy problem. For sufficiently smooth solutions at t = 0 (i.e., for good
initial data decaying fast enough at infinity), (4.133)can be written in the equivalent
integral form
u(x , t) = M[u] ≡ b(t) ∗ u
0
−
t
0
b(t − s) ∗ (|u|
m
u
x
)(s) ds,
= b(t) ∗ u
0
−
1
m+1
t
0
(t − s)
−
2
3
IR
g
x−y
(t−s)
1/3
(|u|
m
u)(y, s) dy.
(4.140)
Here, for solutions of changing sign, u
m
is replaced by |u|
m
. Integration by parts
on the right-hand side of (4.140) needs extra estimates on the behavior of u(x, t)
as x →±∞. For compactly supported u
0
(x ), we may expect that such behavior is
similar to that shown in (4.139). A unique solution of (4.140) is constructed via the
simple iteration
u
n+1
= M[u
n
]forn = 0, 1, ... , u
0
is given, (4.141)
by using the fact that the integral operator M is a contraction in suitable functional
spaces. In view of the slow decay of the Airy function in (4.139) as ξ →−∞,
functional settings are rather tricky; details can be found in [179]. Semigroup ap-
proaches and Banach’s Contraction Principle are effective tools to prove existence
and uniqueness for the Cauchy problem; see [403, Ch. 7] for several advanced ap-
plications. Concerning the behavior of small enough solutions as x →±∞,we
observe that, in iteration (4.141),the regular term |u|
m
u
x
for any m ≥ 0 does not af-
fect the “essence” of asymptotics in the fundamental kernel (4.139). For compactly
supported u
0
, solution u(x, t) of (4.140) will exhibit similar asymptotic decay as
x →∞for arbitrarily small t > 0.
Explicit FBP-compactons via simple ODEs can be constructed for other semilin-
ear PDEs of KdV-type. For instance, the fifth-order KdV-type equation
u
t
+
5
3
(2u + u
4
) + 5u
2
u
xxx
+ u
xxxxx
= 0
possesses the explicit solution with λ = 1 [360]
u(x , t) = B
cos
2
[
1
2
(x−t )]
1−
2
3
cos
2
[
1
2
(x−t )]
, (4.142)
where B =
4
3
. Another KdV-type equation
u
t
+
1
10
u
4
u
x
+ (u
x
)
3
+ u
2
u
xxx
+ u
xxxxx
= 0
admits the solution (4.142) with [570]
B =
2
3
√
10.
All these and other similar solutions need a proper FBP setting. We agree with argu-
ments of Rosenau’s critics of such compactons [494, p. 202], which were sometimes
wrongly treated as solutions of the Cauchy problem in IR × IR
+
.
© 2007 by Taylor & Francis Group, LLC
200 Exact Solutions and Invariant Subspaces
4.4.2 Finite propagation and oscillatory solutions
Example 4.28 (Finite propagation for m ∈ (−1, 0)) Thus, in order to have finite
propagation, we need a singular lower-order term with exponents
m < 0.
For solutions of changing sign, we take the signed mKdV-type equation,
u
t
−|u|
m
u
x
+ u
xxx
= 0inIR × IR
+
(4.143)
(recall the sign change in the second term to ensure a suitable finite propagation).
In general, existence of a solution for m ∈ (−1, 0) can be seen from the inte-
gral equation (4.140) analyzed by Schauder’s Theorem in a proper functional setting
(M is assumed to be compact and map a convex set into itself). It is principal that
uniqueness cannot follow from the integral equation, since M is not a contraction for
the non-Lipschitz nonlinearity |u|
m
u,wherem + 1 ∈ (0, 1).ThisisanOPEN PROB-
LEM.Asusual,uniqueness is associated with the approximation (ε-regularization)
approach as in Section 4.2.4. For second-order parabolic PDEs with singular non-
linear coefficients, this leads to notions of maximal or minimal proper solutions (see
[226, Ch. 7]).
As above, we reveal the interface behavior by using TWs (4.134) satisfying
λf = f
−
1
m+1
| f |
m
f for y > 0, f (0) = 0 (4.144)
(for simplicity, A = 0 in (4.135)). Let us begin by studying the crucial stationary
case λ = 0, where the ODE is simpler,
f
−
1
m+1
| f |
m
f = 0fory > 0, f (0) = 0.
This possesses the positive non-oscillatory solution
f (y) = ϕ
0
y
γ
, where γ =
2
|m|
> 0and
ϕ
0
=
2(m+1)(m+2)
m
2
1
m
,
(4.145)
which describes the behavior also near interfaces for λ = 0; see further asymptotic
expansions below. The function (4.145) being extended by 0 for y ≤ 0 is at least
C
[γ ]−1
at y = 0, and the smoothness increases as m → 0
−
,sinceγ =
2
|m|
→
+∞. Notice also that such solutions satisfy u ∈ C
2
x
for all m ∈ (−1, 0),which
seems difficult to prove for general weak solutions by the integral equation (4.140)
or otherwise. These regularity problems are
OPEN.
It is interesting to estimate the rate of divergence as m → 0
−
of the interface
x = s(t) of solutions u(x, t). For compactly supported u
0
, using estimates in (4.139)
yields, for small fixed t > 0, that
u(x , t) ∼ b(x, t) ∼ t
−
1
3
|x |
t
1/3
−
1
4
as x →−∞.
Consider the expansion for m ≈ 0
−
,
|u|
m
= 1 +m ln|u|+... ,
© 2007 by Taylor & Francis Group, LLC

4 Korteweg-de Vries and Harry Dym Models 201
which is violated for the solution u(x, t) almost everywhere (a.e.) in domains, where
|m ln|u||∼|m||ln|b(x , t)||1.
This characterizes the approximate position of the interface of u(x, t) (indeed, if this
is not true a.e., then u can be again approximated by b). Thus, for the interface, the
following approximate equation holds:
ln|b(s(t), t)|≡−
1
3
lnt −
1
4
ln
|s(t)|
t
1/3
∼−
1
|m|
.
Resolving gives the exponential estimate of the interface position
s(t) ∼−e
4
|m|
as m → 0
−
.
Example 4.29 (Finite propagation and interface equation for m ∈ (−2, −1])
Let us now return to the original mKdV equation (we take A = 0)
u
t
+|u|
m
u
x
+ u
xxx
= 0 ⇒ λ f = f
+
1
m+1
|f |
m
f. (4.146)
Then, for m ∈ (−2, −1), there exists the positive solution
f (y) =
2|m+1|(2+m)
m
2
1
m
y
2
|m|
(1 + o(1)) as y → 0,
for which the interface equation is computed. For
m ≤−2,
such a local TW profile does not exist. Forthe correspondingsecond-order diffusion-
convection equations
u
t
+ u
m
u
x
− u
xx
= 0 (u ≥ 0), (4.147)
with m ≤−2, this means nonexistence of a nontrivial solution u(x, t) ≡ 0forany
compactly supported data u
0
≥ 0; see [226, Sect. 7.5]. For the third and higher-
order evolution PDEs with singular coefficients, similar nonexistence conclusions
are unknown and represent an
OPEN PROBLEM.
Taking into consideration the λ f term in (4.146) yields that, close to the interface
as y → 0
+
,
f (y) = Cy
γ
+ λ
C
(γ +1)(γ +2)
y
γ +2
+ ... , (4.148)
where
γ =
2
|m|
and C
m
=−
2(m+1)(m+2)
m
2
> 0.
The expansion (4.148) determines the corresponding pressure-like variable
v = u
|m|
,
which, for TW profiles, exhibits the analytic-lookingexpansion
f
|m|
(y) = C
|m|
y
2
+ λ
|m|C
|m|
(γ +1)(γ +2)
y
4
+ ... . (4.149)
Recalling the TW structure(4.134),this gives the followingsystem of interfaceequa-
tions at x = s(t), consisting of stationary and dynamic ones:
(u
|m|
)
xx
= 2C
|m|
,
s
= λ =
(γ +1)(γ +2)
24|m|C
|m|
D
4
x
(u
|m|
).
(4.150)
© 2007 by Taylor & Francis Group, LLC

202 Exact Solutions and Invariant Subspaces
For singular second-orderparabolic equations, including (4.147), such interface sys-
tems are rigorously justified by the Sturmian intersection comparison with TW so-
lutions; see examples in [226, Sect. 7.11]. For A = 0 in (4.135), the expansion like
(4.149) contains more terms, so an interface system, such as (4.150), may also in-
clude more equations for m ≈−1
−
; cf. parabolic examples in [226, Sect. 8.5].
In the critical case m =−1, the expansion takes the form (for A = 0)
f (y) =−y
2
ln y −
1
2
y
2
ln(−ln y) −
1
12
λy
4
ln y + ... , (4.151)
so that the interface system is formulated in terms of another pressure variable
v = Q(u) ≡
2u
|lnu|
+ ... as u → 0.
Then Q( f ) = y
2
+ ... and this implies the first stationary interface equation
[Q(u)]
xx
= 2atx = s(t).
Expansion (4.151) then gives the second stationary equation, and the third equation
containing λ that is dynamic. The justification of the interface system (4.150) for
general solutions and the identification of the problem (an FBP, or the Cauchy prob-
lem) remain
OPEN. The non-oscillatory property of the ODE (4.146) at interfaces
suggests that solutions with the behavior (4.148) and (4.151) solve the CP.
Example 4.30 (Solutions of changing sign) Finite interface oscillatory solutions
can be obtained in a KdV-type equation with a lower-order absorption-like term,
u
t
+ uu
x
+ u
xxx
+|u|
−n
u = 0inIR × IR
+
, with n > 0.
The TWs solve
−λf
+ ff
+ f
+|f |
−n
f = 0.
Near the interface at y = 0, keeping two leading terms yields
f
+|f |
−n
f = 0fory > 0, f (0) = 0.
Introducing the oscillatory component
f (y) = y
γ
ϕ(s), where s = ln y, (4.152)
where γ =
3
n
, gives the following ODE:
P
3
[ϕ] =−
ϕ
|ϕ|
n
. (4.153)
This is precisely equation (3.166) that occurred in thin film study in Section 3.7,
where a stable periodic orbit of changing sign was detected for n ∈ (0, n
h
).
Example 4.31 (Self-similar blow-up in (2k+1)th-order PDEs) Neglectingthecon-
vective term uu
x
, consider a general (2k+1)th-order equation with a source,
u
t
= (−1)
k+1
D
2k+1
x
u +|u|
p−1
u in IR × (0, T )(k = 1, 2, ...),
where p > 1. Blow-up similarity solutions are given by
u(x , t) = (T − t)
−
1
p−1
f
x
(T −t )
1/(2k+1)
, where f solves
(−1)
k+1
f
(2k+1)
−
1
2k+1
f
y −
1
p−1
f +|f |
p−1
f = 0.
(4.154)
© 2007 by Taylor & Francis Group, LLC
