Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics
Подождите немного. Документ загружается.


CHAPTER 4
Odd-Order One-Dimensional Equations:
Korteweg-de Vries, Compacton, Nonlinear
Dispersion, and Harry Dym Models
In this chapter, we continue to describe applications of invariant subspaces to nonlinear PDEs
in one dimension, and, unlike the previous chapter, concentrate on nonlinear evolution equa-
tions of odd orders. These models include the famous KdV, nonlinear dispersion, and Harry
Dym-type equations, as well as their higher-order generalizations. Using exact solutions, we
establish interesting similarities between classes of even and odd-order evolution PDEs and
study singularity formation, interface propagation, and oscillatory, changing sign properties of
solutions.
4.1 Blow-up and localization for KdV-type equations
In 1895, Korteweg and de Vries introduced the famous third-order KdV equation of
shallow water waves
v
t
= v
xxx
+ 2vv
x
in IR × IR (4.1)
and its explicit soliton
v(x , t) =
3
2cosh
2
[
1
2
(x+t )]
, (4.2)
which is the traveling wave solution moving to the left with unit velocity.
∗
This and
other multi-soliton solutions play a determining role in general water waves theory
and theory of integrable PDEs. By scaling x → λx, t → λ
3
t,andv → Cv, (4.1)
reduces to v
t
= v
xxx
+ 2Cλ
2
vv
x
and takes standard forms
v
t
= v
xxx
+ vv
x
for C =
1
2λ
2
, or
v
t
= v
xxx
+ 6vv
x
for C =
3
λ
2
.
Setting v = u
x
in (4.1) and integrating once gives the potential KdV equation
u
t
= u
xxx
+ (u
x
)
2
. (4.3)
Then the soliton (4.2) is transformed into the front moving traveling wave, which is
reconstructed from (4.2) by the inverse transformation
u(x , t) =
x
−∞
v(z, t) dz.
∗
It has long been recognized that both the KdV equation and its soliton solution were derived earlier by
Boussinesq in 1872 [75], so the abbreviation BKdV can be used for (4.1).
© 2007 by Taylor & Francis Group, LLC

164 Exact Solutions and Invariant Subspaces
4.1.1 Quadratic operators and invariant subspaces
Consider a third-order PDE with a more general quadratic operator associated with
that in (4.3),
u
t
= F[u] = αu
xxx
+ β(u
x
)
2
+ γ u
2
. (4.4)
Let us begin with trigonometric subspaces for such simple quadratic operators al-
ready studied in Section 1.4.
Proposition 4.1
Operator
F
in
(4.4)
admits
W
3
= L{1, cos x , sin x}
if
β = γ
.
Looking for the solutions
u(x , t) = C
1
(t) + C
2
(t) cos x + C
3
(t) sin x ∈ W
3
for t ∈ IR
yields that the PDE (4.4) on W
3
is equivalent to the DS
C
1
= β(C
2
1
+ C
2
2
+ C
2
3
),
C
2
=−αC
3
+ 2βC
1
C
2
,
C
3
= αC
2
+ 2βC
1
C
3
.
These exact periodic solutions admit a soliton-traveling wave representation,
u(x , t) = C
1
(t) + C
2
(t) cos(x ± t) + C
3
(t) sin(x ±t), (4.5)
with asimilar DS for the coefficients.Such moving 2π -periodicsoliton-likesolutions
may blow-up in finite time. There exist 2D invariant reductions of such periodic
moving waves.
Proposition 4.2
If
β = γ
and
α =±1
in
(4.4)
, then there exist exact solutions
u(x , t) = C
1
(t) + C
2
(t) cos(x ∓ t).
4.1.2 Applications to blow-up
Example 4.3 (Blow-up and localization) Consider the KdV equation with source
u
t
= u
xxx
+ (u
x
)
2
+ u
2
. (4.6)
Here, α = β = γ = 1, so by Proposition 4.2 there exist solutions on
W
−
2
= L{1, cos(x − t)},
i.e.,
u(x , t) = C
1
(t) + C
2
(t) cos(x − t), (4.7)
C
1
= C
2
1
+ C
2
2
,
C
2
= 2C
1
C
2
.
(4.8)
According to (4.7), the DS describes the time-deformation of a moving 2π-periodic
soliton. An explicit self-similar solution in separate variables appears for C
1
= C
2
,
yielding the single ODE C
1
= 2C
2
1
, and the solution on
˜
W
1
= L{cos
2
[
1
2
(x −t)]}
given by
u(x , t) =
1
T −t
cos
2
[
1
2
(x −t)], (4.9)
© 2007 by Taylor & Francis Group, LLC
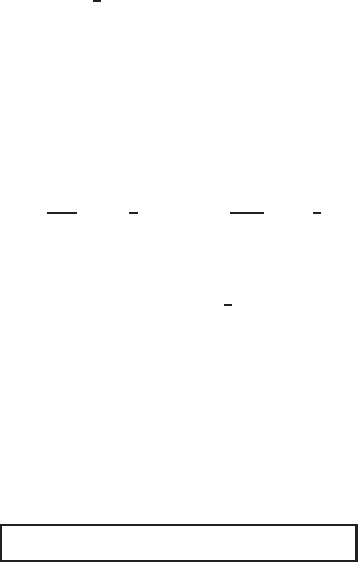
4 Korteweg-de Vries and Harry Dym Models 165
where T > 0isthefinite blow-up time. This is a blow-up soliton solution moving to
the right with constant unit speed and blowing up as t → T
−
everywhere,excluding
the points x
k
= T + π(2k + 1), k = 0, ±1, ...,whereu(x, T
−
) = 0. It is easy to
detect the following localization property of these blow-up solutions:
u(x
k
, t) =
1
4
(T − t) + ... → 0ast → T,
so that the solution remains bounded at all points x = x
k
and tends to infinity at any
other x ∈ IR . Notice that (4.9) is a classical analytic periodic solution of the non-
degeneratePDE (4.6) on IR ×(0, T ). To monitor a one-humpwave of such solutions
on {|x − t| <π}, a proper FBP should be posed. This will be discussed later for
degenerate third-order operators.
Returning to the quadratic DS (4.8) (cf. Proposition 3.18 for more general DSs),
we easily solve it explicitly and obtain the following solutions:
u(x , t) =
1
T −t
cos
2
[
1
2
(x −t)] +
1
T
1
−t
sin
2
[
1
2
(x −t)].
It follows that, for T
1
> T > 0, they asymptotically converge to the separate vari-
ables solution (4.9), in the sense that the rescaled function satisfies
w(x, t) ≡ (T − t)u(x, t) → cos
2
[
1
2
(x − T )]ast → T. (4.10)
The general asymptotic stability of this localized blow-up pattern leads to the study
of the rescaled PDE for w(x, t),
w
τ
= F
∗
[w] ≡ w
xxx
+ (w
x
)
2
+ w
2
− w, where τ =−ln(T − t),
and proving convergence (4.10) (up to translation in x) for periodic initial data. Sta-
bility analysis demands a sharp upper bound for the rescaled orbit {w(·,τ)},which
remains an
OPEN PROBLEM for general initial data. Similar conclusions apply to
higher odd-order PDEs, such as
u
t
= D
2m+1
x
u + (u
x
)
2
+ u
2
, m = 2, ... ,
for which blow-up stability problems are OPEN.
4.2 Compactons and shocks waves in higher-order quadratic nonlinear
dispersion models
In the next sections we study exact solutions of a number of quasilinear degenerate
odd-order PDEs which have many applications and still rather poor mathematical
understanding.
4.2.1 Compactons on 3D trigonometric subspace
As a typical simple example, consider the fifth-order quadratic operator,
F
5
[u] = α(u
2
)
xxxxx
+ β(u
2
)
xxx
+ γ(u
2
)
x
. (4.11)
Proposition 4.4
Operator
(4.11)
admits
W
3
= L{1, cos x , sin x}
iff
16α − 4β + γ = 0. (4.12)
© 2007 by Taylor & Francis Group, LLC
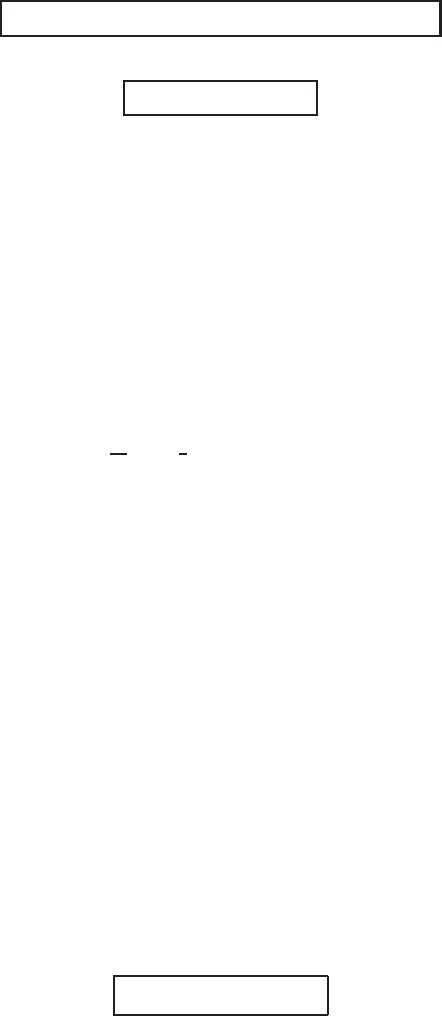
166 Exact Solutions and Invariant Subspaces
Example 4.5 (Dynamics on W
3
around compactons in quadratic models) Con-
sider the quintic nonlinear dispersion equation
u
t
= α(u
2
)
xxxxx
+ β(u
2
)
xxx
+ γ(u
2
)
x
in IR × IR . (4.13)
For α = 0, β = γ = 1, this is the third-order Rosenau–Hyman (RH) equation
u
t
= (u
2
)
xxx
+ (u
2
)
x
, (4.14)
which models the effect of nonlinear dispersion in the pattern formation in liquid
drops [496]. It is the K (2, 2) equation from the general K (m, n) family of nonlinear
dispersion equations
u
t
= (u
n
)
xxx
+ (u
m
)
x
(u ≥ 0), (4.15)
that also models phenomena of compact pattern formation, [491, 492]. Such PDEs
appear in curve motion and shortening flows [494]. The K (m, n) equation (4.15)
with n > 1 is degenerated at u = 0, and therefore may exhibit finite speed of prop-
agation and admit solutions with finite interfaces. Rigorously speaking, these ques-
tions, especially for degenerate higher-order models, lead to several
OPEN PROB-
LEMS to be discussed.
Thecrucialadvantageof the RH equation (4.14)is that it possessesexplicit moving
compactly supported soliton-type solutions, called compactons [496]:
u(x , t) =
−
4λ
3
cos
2
[
1
4
(x −λt)], if |x − λt|≤2π,
0, if |x −λt| > 2π,
(4.16)
where, for λ<0, the solution is nonnegative; see Figure 4.1. These are the TW
patterns with two interfaces moving to the left. Taking λ>0 yields the negative
compacton moving to the right.
For the fifth-orderPDE (4.13),compactonsolutionswerefirstconstructedin [147],
where the more general K (m, n, p) family of PDEs
u
t
+ β
1
(u
m
)
x
+ β
2
(u
n
)
xxx
+ β
3
D
5
x
(u
p
) = 0 (m, n, p > 1),
was introduced. Some of these equations will be treated later on. Equation (4.13) is
also associated with the family Q(l, m, n) of more general quintic evolution PDEs
with nonlinear dispersion,
u
t
+ a(u
m+1
)
x
+ ω
u(u
n
)
xx
x
+ δ
u(u
l
)
xxxx
x
= 0, (4.17)
possessing multi-hump, compact solitary solutions [499].
Using first the particular quadratic model (4.13), we will discuss the dynamic in-
terface equations and a general mathematical meaning of compactons. The first im-
portant question is to establish which kind of FBPs or the Cauchy problem such
compactons may be solutions of. In addition, as usual, our goal is to show that there
exist extra explicit finite-dimensional dynamics on invariant subspaces around those
compactons.These results can be extended to general odd-order quadratic dispersive
PDEs, such as
u
t
=
(k)
α
k
D
2k+1
x
(u
2
).
© 2007 by Taylor & Francis Group, LLC

4 Korteweg-de Vries and Harry Dym Models 167
u(x , t)
t
1
t
2
t
3
t
1
< t
2
= 0 < t
3
x
0
λ
λ
2π
−2π
Figure 4.1 Moving compacton (4.16) with λ<0 of the RH equation (4.14).
Let us return to the fifth-order PDE (4.13) and, assuming (4.12), look for exact
solutions on W
3
,
u(x , t) = C
1
(t) + C
2
(t) cos x + C
3
(t) sin x , (4.18)
C
1
= 0,
C
2
= µC
1
C
3
,
C
3
=−µC
1
C
2
,
(4.19)
where µ = 2(α−β +γ)= 0. In this case, from the first ODE, C
1
(t) = A, a constant,
and the last two yield
C
2
2
+ C
2
3
= B
2
,
where B = 0 is a constant of integration. This gives the explicit solutions
u(x , t) = A + B cos(x + µAt). (4.20)
In the particular case A = B, denoting µ A =−λ, and assuming that
λ
µ
< 0, we
obtain a nonnegative traveling wave solution
u(x , t) =−
2λ
µ
cos
2
[
1
2
(x −λt)]. (4.21)
Choosing the one-hump profile on the moving interval |x − λt|≤π and setting
u(x , t) = 0for|x − λt| >πyields a compacton, which is similar to (4.16) in
Figure 4.1. Appropriate FBP setting for such solutions of the higher-order PDE will
be studied in Section 4.2.3.
It turns out that there exists an intriguingsimilarity between compacton patterns in
nonlinear dispersion media and localized blow-up structures in dissipative reaction-
combustion models that were studied in the previous chapters.
Example 4.6 (Comparison of compactons and regional blow-up) Explicit TW
compactonsalso exist for the nonlinear dispersion KdV-type equations with arbitrary
power nonlinearities (formulae will be given shortly)
v
t
= (v
n+1
)
xxx
+ γ(v
n+1
)
x
, with n > 0andγ =
(n+1)
2
n
2
(v ≥ 0), (4.22)
© 2007 by Taylor & Francis Group, LLC

168 Exact Solutions and Invariant Subspaces
where the parameter γ>0 is chosen for convenience and can be scaled out. This is
the K (1 + n, 1 + n) model, [496].
Combustion model: regional blow-up. Firstly, we compare such compactons with
blow-up solutions of the following parabolic reaction-diffusion equation:
v
t
= (v
n+1
)
xx
+ γv
n+1
. (4.23)
In (4.22), the right-hand side is the derivative D
x
of that in (4.23). Mathematically,
these equations belong to entirely different types of PDEs.
In the mid 1970s, Kurdyumov, with his former PhD students, Mikhailov and
Zmitrenko, (see [510]) discovered the phenomenon of heat and combustion local-
ization by studying properties of the following Zmitrenko–Kurdyumov solution of
the equation (4.23):
v
S
(x , t) = (T − t)
−
1
n
f (x), (4.24)
where T > 0 is the blow-up time, and f satisfies the ODE
1
n
f = ( f
n+1
)
+ γ f
n+1
for x ∈ IR . (4.25)
It turned out that (4.25) possesses the explicit compactly supported solution
f (x) =
n
(n+1)(n+2)
cos
2
(
x
2
)
1
n
, if |x|≤π,
0, if |x | >π.
(4.26)
The striking regional blow-up (the so-called S-regime of blow-up, [510]) described
by the solution (4.24), (4.26) is as follows: v
S
(x , t) →∞as t → T
−
for all |x| <π
only and v
S
(x , t) ≡ 0 otherwise. This is the localization phenomenon on the interval
{|x | <π} of the length 2π that is called the fundamental length of such a diffusive
and combustion medium. Notice that (4.24) is a standard continuous weak solution
of the PDE (4.23) on IR × (0, T ).
Regional blow-up in a quasilinear wave equation. Secondly, a similar exact solu-
tion exists for the quasilinear hyperbolic equation
v
tt
= (v
n+1
)
xx
+ γv
n+1
, where
v
S
(x , t) = (T − t)
−
2
n
˜
f (x) ⇒
2
n
2
n
+ 1
˜
f = (
˜
f
n+1
)
+ γ
˜
f
n+1
. (4.27)
Here f is given by a scaled function (4.26),
˜
f (x) =
2(n+2)
n
1/n
f (x).
Compactons. Thirdly, returning to the compactons of (4.22) of the TW structure
v
c
(x , t) = f (y), y = x − λt, (4.28)
we find that f satisfies the ODE
−λf
= ( f
n+1
)
+ γ(f
n+1
)
,
which gives, on integration once,
−λ f = ( f
n+1
)
+ γ f
n+1
+ D, (4.29)
where D ∈ IR is the constant of integration. Setting D = 0 yields that the blow-up
© 2007 by Taylor & Francis Group, LLC

4 Korteweg-de Vries and Harry Dym Models 169
ODE (4.25) and the compacton equation (4.29) coincide, provided that
−λ =
1
n
or −λ =
2
n
2
n
+ 1
to match (4.27)
.
This yields the compacton solution(4.28) with the same compactlysupportedprofile
(4.26) with translation x → y = x − λt. Therefore, the blow-up solutions (4.24),
(4.27) and the compacton solution (4.28) are essentially of a similar mathematical
(both the ODE and PDE) nature, and, possibly,more than that. This reflects a certain
universality principle of compact structure formation in nonlinear evolution PDEs.
On dynamics on invariant subspaces. The quasilinear heat equation (4.23) admits
further restriction to the standard invariant subspace that we will briefly discuss. The
pressure transformation u = v
n
in (4.23) yields
u
t
= F[u] ≡ (n + 1)
uu
xx
+
1
n
(u
x
)
2
+ nγ u
2
.
Operator F is known to preserve the 2D subspace W
2
= L{1, cos x },sothereexist
exact solutions
u
S
(x , t) = C
1
(t) + C
2
(t) cos x, (4.30)
C
1
=
(n+1)
2
n
C
2
1
+
n+1
n
C
2
2
,
C
2
=
(n+1)(n+2)
n
C
1
C
2
.
ThisDS can beintegratedinquadratures,so (4.30)describessome exceptionalevolu-
tion and blow-up properties.Following [218] (or [509, p. 32]),where a detailed anal-
ysis and proofscan be found,we comment that, as t → 0
+
, the solution takes Dirac’s
delta as the initial function; see Figure 4.2. Next, the solution amplitude u(0, t) de-
creases for some t ∈ (0, t
3
), and, after that, the solution starts to increase, and finally
blows up and approaches as t → T
−
the separate variables solution (4.24). Hence,
the interfaces s
±
(t) of the compactly supported blow-up solution (4.30) converge to
±π respectively, as explained in Figure 4.2.
A similar invariant subspace analysis applies to the compacton equation (4.22),
but only for n = 1, where the general solution (4.20) is not that consistent. It seems
that, for n = 1, interesting invariant subspaces do not exist. Further interpretation is
performed by using partially invariant subspaces. We explain this in Section 7.2.
Example 4.7 (Higher-order signed PDEs: compactons and regional blow-up)A
similar, but not explicit, compacton–regionalblow-up universalityis availablefor the
quintic signed nonlinear dispersion PDEs, such as
v
t
= α
|v|
n
v
xxxxx
+ β
|v|
n
v
xxx
+ γ
|v|
n
v
x
(n > 0), (4.31)
and its parabolic reaction-diffusion counterpart (α<0 for parabolicity)
v
t
= α
|v|
n
v
xxxx
+ β
|v|
n
v
xx
+ γ |v|
n
v.
Both equationsare written for oscillatory solutionsof changingsign; see more details
in Section 4.3. Compactons (4.28) for (4.31) and the blow-up pattern (4.24) are then
governed by the same quasilinear degenerate ODE
−λf = α
| f |
n
f
(4)
+ β
| f |
n
f
+ γ | f |
n
f, with λ =−
1
n
< 0.
© 2007 by Taylor & Francis Group, LLC

170 Exact Solutions and Invariant Subspaces
u
S
(x , t)
t
1
≈ 0
t
2
t
3
t
4
t
5
t
6
≈ T
x
0
π
−π
s
−
(t
4
)
s
+
(t
4
)
Figure 4.2 Non-monotone evolution of the blow-up solution (4.30); 0 < t
1
< ... < t
6
< T .
For instance, consider two equations
u
t
=−
|u|
n
u
xxxxx
+
|u|
n
u
x
(dispersive: compactons), and
u
t
=−
|u|
n
u
xxxx
+|u|
n
u (parabolic: blow-up).
(4.32)
Then the compacton for the first PDE is (4.28) and the localized blow-up pattern for
the second is (4.24), where f = f (y) solves
−(| f |
n
f )
(4)
+|f |
n
f =
1
n
f in IR .
Recall that, for the CP, similar to TFEs (Section 3.7), we are interested in solutions
of maximal regularity with the following behavior:
f (y) ∼ (y
0
− y)
4
n
ϕ(ln(y
0
− y))
near the interface at y = y
−
0
, with, say, a bounded, periodic oscillatory component
ϕ(s). Figure 3.5(a) illustrates such oscillatory behavior. After the natural change, this
gives the ODE with a non-Lipschitz nonlinearity,
F =|f |
n
f ⇒ F
(4)
= F −
1
n
F
−
n
n+1
F in IR . (4.33)
Unlike the second-order case (4.26), for the CP, an explicit compactly supported so-
lution f is not available. Proving existence and multiplicity results for such higher-
order ODEs is a difficult
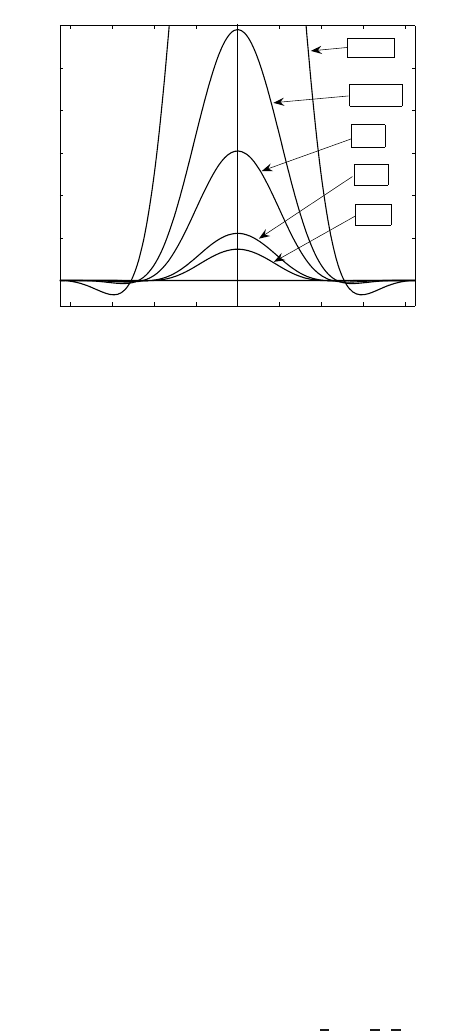
OPEN PROBLEM to be tackled numerically. First, the sim-
plest geometric patterns, F
1
(y) in 1D for various n > 0, are presented in Figure 4.3.
Notice the clear oscillatory behavior of solutions close to interfaces. This is a key
feature for the CP that was studied in Section 3.7 for TFEs, and will be continued
and extended to odd-order PDEs.
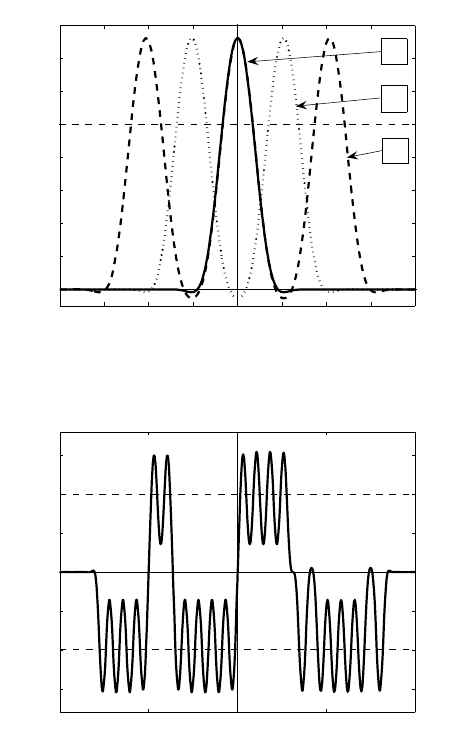
As a rule, such localized profiles F (or f ) are not unique. Three patterns denoted
by F
1
, F
2
,andF
3
for n = 1, which exhibit a clear “approximate geometric order,”
are shown in Figure 4.4. Each F
k
has precisely k dominant maxima (in view of
© 2007 by Taylor & Francis Group, LLC
4 Korteweg-de Vries and Harry Dym Models 171
8 6 4 2 0 2 4 6 8
0
0.5
1
1.5
2
2.5
3
y
F(y)
n=0.5
n=0.75
n=1
n=2
n=3
Figure 4.3 Compactly supported solutions of (4.33) for various n > 0.
the oscillatory behavior near interfaces, this Sturmian property is rigorously true
for the second-order ODEs only). In general, we expect many different solutions
F
σ
with a multiindex σ of arbitrary length that characterizes oscillatory behavior
of the pattern about equilibria F
±
=±n
−(n+1)/n
and F
0
= 0. Some countable
sequences of such blow-up-compacton patterns {F
k
, k ≥ 1} can be attributed to
Lusternik–Schnirel’man classic variational category (genus) theory from the 1930s;
see Krasnosel’skii–Zabreiko [355, Ch. 8]). It is important that the ODE (4.33) is
variational.
Figure 4.5 shows a complicated multi-hump pattern, F
σ
, with the multiindex
σ ={−8, +4, −10, +8, −2, 2, −8, 2, −2}.
Here, the first number“-8” reflects the first eight intersections with F
−
=−1, fol-
lowed by “+4”, i.e., four intersections with F
+
=+1, next “-10” means ten inter-
sections with -1, etc. The number of intersections with F
0
= 0 is given without the
sign, such as “2”, that occurs two times in this multiindex. We omit mentioning the
unique, transversal intersection with zero, i.e., “1”, everywhere in this sequence. It
seems that equation (4.33) admits compactly supported solutions F
σ
(y) of arbitrary
“chaotic” complexity, corresponding to any suitable finite multiindex σ . A precise
meaning of similar chaotic orbits for fourth-order ODEs (though of a different, non-
oscillatory type close to interfaces as F → 0; this destroysa standardhomotopy-like
approach to such orbits) is explained in [459, p. 198]. For the above nonlinear dis-
persion equation in (4.32), this is a compacton moving with the velocity λ =−1.
Similar standing blow-up patterns exist for the hyperbolic PDE
u
tt
=−
|u|
n
u
xxxx
+|u|
n
u (hyperbolic: blow-up),
where the only change in (4.33) is in the multiplier
1
n
→
2
n
2
n
+ 1
. Therefore, as
formerly, (4.28) and (4.24) give countable spectra of both moving compactons for
© 2007 by Taylor & Francis Group, LLC
172 Exact Solutions and Invariant Subspaces
20 15 10 5 0 5 10 15 20
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
y
F(y)
F
1
F
2
F
3
Figure 4.4 Three solutions of (4.33) for n = 1.
100 50 0 50 100
1.5
1
0.5
0
0.5
1
1.5
y
F(y)
Figure 4.5 A complicated compacton pattern of the ODE (4.33) for n = 1.
nonlinear dispersion PDEs and standing localized blow-up patterns in parabolic and
hyperbolic problems.
4.2.2 On shock and rarefaction waves in PDEs with nonlinear dispersion
As a key feature of quasilinear odd-order PDEs, it is important to note that suffi-
ciently smooth profiles and evolution behavior exhibited by compactons and other
solutions to be described are not generic for many such equations (excluding some
special, “integrable” ones). This is in striking contrast with even-order quasilinear
parabolic PDEs, which, according to classical theory, exhibit a strong internal reg-
© 2007 by Taylor & Francis Group, LLC
