Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics
Подождите немного. Документ загружается.


3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 133
Recall that, for second-order operators in Section 1.4, similar different trigono-
metric and exponential subspaces occurred for the unique remarkable operator
F
1
[u] = uu
xx
− (u
x
)
2
= F
rem
[u]
. (3.127)
Its natural fourth-order analogy corresponds to β = 1 in (3.125),
F
1
[u] =−uu
xxxx
+ (u
xx
)
2
. (3.128)
Using exponential functions. Continuing to detect other invariant properties, us-
ing Proposition 3.19, consider the following differential operator for functions u =
u(x , t) of two independent variables:
ˆ
F[u] = u
t
− F
β
[u].
We choose solutions in the form of
u(x , t) = C
1
(t) + C
2
(t)x +C
3
(t)e
γ(t )x
, (3.129)
with a function γ(t) to be specified. Our analysis here is similar to that shown in
Example 1.37, so for functions (3.129) we find
ˆ
F[u] = C
1
+ C
2
x +
C
3
+ γ
4
C
1
C
3
− (1 − β)γ
3
C
2
C
3
e
γ x
+
γ
+ γ
4
C
2
C
3
xe
γ x
.
Then the ODE γ
=−γ
4
C
2
is a characterization of an invariant set M in the linear
subspace (a partially invariant module) W
3
,sothat
ˆ
F : M → W
3
.
Example 3.20 The fourth-order PDE
u
t
=−uu
xxxx
+ β(u
xx
)
2
+ (1 − β)u
x
u
xxx
+ µu + ν
admits solutions (3.129), where the coefficients satisfy the DS
C
1
= µC
1
+ ν,
C
2
= µC
2
,
C
3
=−γ
4
C
1
C
3
+ (1 − β)γ
3
C
2
C
3
+ µC
3
,
γ
=−γ
4
C
2
.
The second and the fourth ODEs give all possible functions γ(t).
Using trigonometric functions. According to Proposition 3.19, we now deal with
operator (3.128). Then, the fifth-order operator
˜
F[u] =
d
dx
F
1
[u] ≡−uu
xxxxx
− u
x
u
xxxx
+ 2u
xx
u
xxx
(3.130)
also preserves 3D trigonometric subspaces in (3.126) for arbitrary γ = 0. The extra
differentiation in (3.130) is necessary to create a single ODE for γ(t). Recall that,
similarly, in Example 1.36 we used the quadraticoperator of the RPJ equation as the
derivative of (3.127). Such invariant properties of the corresponding operator
ˆ
F[u] = u
t
−
˜
F[u]
are listed in the following example.
© 2007 by Taylor & Francis Group, LLC

134 Exact Solutions and Invariant Subspaces
Example 3.21 The sixth-order semilinear parabolic equation
u
t
= εu
xxxxxx
− uu
xxxxx
− u
x
u
xxxx
+ 2u
xx
u
xxx
+ µu + ν
possesses exact solutions
u(x , t) = C
1
(t) + C
2
(t)x +C
3
(t) cos(γ (t)x ) + C
4
(t) sin(γ (t)x),
C
1
= µC
1
+ ν,
C
2
= µC
2
,
C
3
=−εγ
6
C
3
− γ
5
C
1
C
4
− γ
4
C
2
C
3
+ µC
3
,
C
4
=−εγ
6
C
4
+ γ
5
C
1
C
3
− γ
4
C
2
C
4
+ µC
4
,
γ
=−γ
5
C
2
.
3.6 2mth-order thin film operators and equations
We describe basic subspaces and extensions for 2mth-order TFEs, such as (3.16).
3.6.1 Basic polynomial subspaces
Consider the standard higher-order quadratic thin film operator
F[u] = (−1)
m+1
D
x
uD
2m−1
x
u
.
Since M(l) = 2l − 2m, i.e., F[x
l
] ∼ x
2l−2m
, equating 2l − 2m = l yields the
following basic subspace:
W
2m+1
= L{1, x, x
2
, ..., x
2m
}. (3.131)
This makes it possible to study various singularity formation phenomena, such as
finite time extinction, quenching, turning points, interface dynamics, etc., for the
corresponding TFE with absorption
u
t
= (−1)
m+1
D
x
uD
2m−1
x
u
− 1.
The corresponding exact solutions are given by
u(x , t) =
C
1
(t) + C
2
(t)x +C
3
(t)x
2
+ ... + C
2m+1
(t)x
2m
+
,
where {C
i
(t)} solve a DS. These nonnegative functions are weak solutions of FBPs
with Stefan–Florin free-boundary conditions, which can be detected in a manner
similar to above lower-order models (cf. a simpler derivation below).
Example 3.22 (Cubic TFE) In the cubic equation
u
t
= F[u] ≡ (−1)
m+1
D
2m
x
au
3
+ bu
2
+ cu
the operator admits the basic subspace W
m+1
= L{1, x, x
2
, ..., x
m
}. Free-boundary
and asymptotic analysis of the extinction and quenching behavior in the correspond-
ing absorption model
u
t
= F[u] −1onW
m+1
,
are similar to the fourth-order models in Section 3.2.
© 2007 by Taylor & Francis Group, LLC
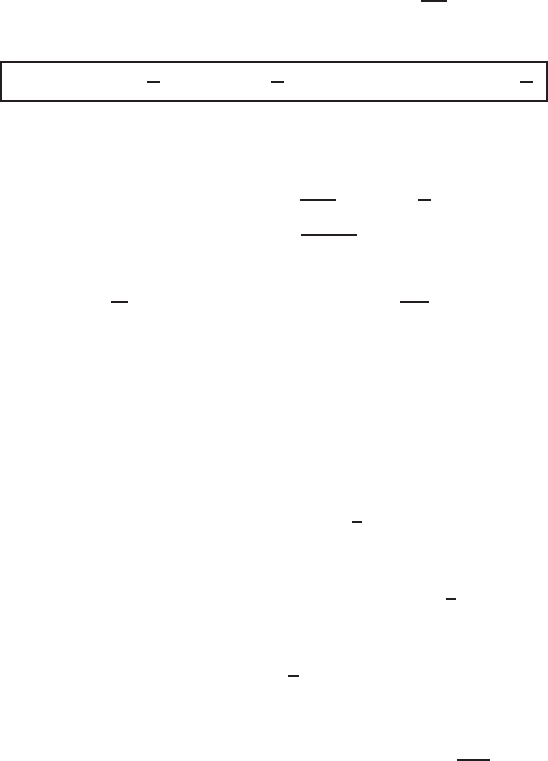
3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 135
3.6.2 Solutions with zero contact angle conditions
In order to obtain solutions v(x, t) satisfying m + 1 free-boundary conditions at the
interface, including m − 1 generalized zero contact angle conditions and a zero-flux
condition, i.e.,
v = v
x
= ... = D
m−1
x
v = v D
2m−1
x
v = 0atx = s(t), (3.132)
we need to introduce models with specific algebraic and invariant properties. As
above, we consider two types of such equations.
Example 3.23 (Strong absorption)Thefirst model is the 2mth-order TFE with
strong absorption
v
t
= (−1)
m+1
D
x
v D
2m−1
x
v
− v
m−1
m
. (3.133)
Setting v = u
m
yields the operator F
m+1
of the algebraic homogenuity m + 1,
u
t
= F
m+1
[u] −
1
m
≡ (−1)
m+1
1
m
uD
2m
x
u
m
+ u
x
D
2m−1
x
u
m
−
1
m
. (3.134)
F
m+1
admits W
3
= L{1, x , x
2
}, and hence, the FBP (3.133), (3.132) has solutions
v(x , t) = u
m
(x , t) =
C
1
(t) + C
3
(t)x
2
m
+
, (3.135)
C
1
= (−1)
m+1
(2m)!
m
C
1
C
m
3
−
1
m
,
C
3
= (−1)
m+1
(2m+1)!
m
C
m+1
3
.
The dynamic interface equation is readily derived from (3.134),
s
=−
1
u
x
u
t
= S[u] ≡ (−1)
m
D
2m−1
x
u
m
+
1
mu
x
at x = s(t).
This equation is the main regularity condition for solvability of the degenerate PDE,
written in terms of the vonMises variable X = X (u, t) near the interface. Themanip-
ulations become more technical for large m than those performed before for lower-
order equations. Exact solutions (3.135) describe singular phenomenaof quenching,
extinction, and others.
On the Cauchy problem. For solutions of changing sign that exhibit the maximal
regularity, we consider the TFE with absorption
v
t
= (−1)
m+1
D
x
|v|D
2m−1
x
v
−|v|
−
1
m
v in IR × IR
+
. (3.136)
As in Example 3.10, we use the TWs v(x, t) = f (x − λt) satisfying the ODE
−λf
= (−1)
m+1
(| f |f
(2m−1)
)
−|f |
−
1
m
f,
or, neglecting the non-stationary, λ-dependent term for small f ,
(−1)
m+1
(| f |f
(2m−1)
)
−|f |
−
1
m
f = 0fory > 0, f (0) = 0.
This gives the following oscillatory structure of solutions:
f (y) = y
γ
ϕ(s), s = ln y, where γ =
2m
2
m+1
, (3.137)
which applies to many higher-order ODEs. Here the oscillatory component ϕ(s)
© 2007 by Taylor & Francis Group, LLC

136 Exact Solutions and Invariant Subspaces
solves a 2mth-order autonomous ODE. Such ODEs will be shown to admit oscil-
latory, periodic solutions that describe different types of multiple zeros of solutions
of the PDE (3.136); see Figure 3.5(a) as an illustration. The exponent γ in the enve-
lope in (3.137) is such that
γ>2m − 2, so that f (y) = o(y
2m−2
) as y → 0.
Hence, maximal regularity solutions satisfy on the interface the conditions
f
(0) = ... = f
(2m−2)
(0) = 0,
and are smoother than those of the FBP, which are O(y
m
), as (3.132) suggests.
Example 3.24 (Backward diffusion perturbation) The second model includes a
special divergent second-order operator generating an extra instability feature of the
thin film flow,
v
t
= (−1)
m+1
D
x
v D
2m−1
x
v
−
v
1
m
v
x
x
, or
u
t
= (−1)
m+1
1
m
uD
2m
x
u
m
+ u
x
D
2m−1
x
u
m
−
uu
xx
+ m(u
x
)
2
for v = u
m
. For solutions (3.135), the following DS is obtained:
C
1
= (−1)
m+1
(2m)!
m
C
1
C
m
3
− 2C
1
C
3
,
C
3
= (−1)
m+1
(2m+1)!
m
C
m+1
3
− 2(2m + 1)C
2
3
.
It follows from the second ODE that, given an initial value C
3
(0)<0, the following
holds:C
3
(t) →−a =−[(2m −1)!]
−1/(m−1)
as t →∞. This means the exponential
stabilization to unstable stationary solutions,
u(x , t) = (B − ax
2
)
+
+ O(e
−γ
m
t
), with γ
m
= (m − 1)(2m + 1)a,
where B > 0 is a constant, depending on the initial data.
3.6.3 Extensions of polynomial subspaces
Consider a generalization of the thin film operator,
F[u] = (−1)
m+1
uD
2m
x
u + βu
x
D
2m−1
x
u
(β ∈ IR ). (3.138)
Here we keep two monomial operators of the same total differential order, where
i + j = k, with k = 2m; cf. the general quadratic operator (1.86). The next result is
proved directly.
Proposition 3.25
Operator
(3.138)
preserves the following extensions of the sub-
space
(3.131)
:
W
2m+2
= L{1, x , ..., x
2m
, x
2m+1
}
iff
β = β
1
=−
2
2m+1
; (3.139)
W
2m+3
= L{1, x , ..., x
2m
, x
2m+1
, x
2m+2
}
iff
β = β
2
=−
3
2m+2
. (3.140)
Further extensions of polynomial subspaces are not possible for operator (3.138),
but can be obtained for other similar operators containing extra monomials of the
© 2007 by Taylor & Francis Group, LLC

3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 137
same exponent M(l) with more free parameters β, γ , etc. (see (3.142) below). Con-
structing the corresponding exact solutions leads to higher-order DSs. In the case of
(3.140), the DS is simplified if we take only even polynomials by introducing
W
even
m+2
= L{1, x
2
, ..., x
2m
, x
2m+2
} (3.141)
that is also invariant under operator (3.138) for β = β
2
. Such subspacesare sufficient
for studying most singularity,free boundary,and asymptotic phenomena for the TFE
with symmetric initial data. Using subspaces of even functions, we formulate the
following pretty general observation that is convenient for future computations and
was observed before in particular cases.
Proposition 3.26
If subspace
(3.141)
is invariant under a polynomial quadratic op-
erator with constant coefficients
(
again, in each monomial,
i + j = k = 2m)
F[u] = (−1)
m+1
uD
2m
x
u + βu
x
D
2m−1
x
u + γ u
xx
D
2m−2
x
u + ...
(3.142)
for some
β =
˜
β
2
depending on
γ
and other parameters. Then subspace in
(3.140)
is
also invariant under
F
.
Proof. Indeed, taking
u = C
1
+ C
3
x
2
+ ... + C
2m+1
x
2m
+ C
2m+3
x
2m+2
(3.143)
and controlling the higher-degree term only yields
F[u] = (β −
˜
β
2
)A
m
(C
2m+3
)
2
x
2m+4
+ ... , (3.144)
where A
m
= 0 is a constant. The second (omitted) term contains x
2m+2
∈ W
even
m+2
.
Hence, always F[u] ∈ W
even
m+2
iff β =
˜
β
2
.Takingnowu from subspace (3.140),
u = C
2m+3
x
2m+2
+ C
2m+2
x
2m+1
+ ... , where C
2m+3
= 0
(C
2m+3
= 0 is easy), and performing the translation x → x − a gives
u = C
2m+3
x
2m+2
+
C
2m+2
− (2m + 2)aC
2m+3
x
2m+1
+ [·]x
2m
+ ... .
Choose now a such that C
2m+2
− (2m + 2)aC
2m+3
= 0tovanishthesecondco-
efficient. Then we get that the last two terms contain x
2m+2
and x
2m
as in (3.143).
Hence, the argument for even degree polynomials applies, so the term with x
2m+3
does not appear in F[u].
Similarly, a more general result holds, which applies to arbitrary quadratic opera-
tors with monomials of the same total order such as (1.86).
Lemma 3.27
If operator
(3.142)
admits
W
(1)
2m+2
= L{1, x , ..., x
2m−1
, x
2m
, x
2m+2
}
(
a subspace with “1-gap”
)
, then it admits
W
2m+3
= L{1, x, ..., x
2m
, x
2m+1
, x
2m+2
}
(
the full subspace
)
.
Remark 3.28 (Open problem: gap completing) The result is true for the “2-gap”
subspace W
(2)
2m+1
= L{1, x , ..., x
2m−3
, x
2m−2
, x
2m
, x
2m+2
}.AsanOPEN PROBLEM,
taking the “(m+1)-gap” subspace of even polynomials (3.141), we conjecture that if
F : W
even
m+2
→ W
even
m+2
,thenF : W
2m+3
→ W
2m+3
. (For cubic operators, this is not
true; see Proposition3.5.) Invariantsubspaces with more general distribution of gaps
are also unclear.
© 2007 by Taylor & Francis Group, LLC

138 Exact Solutions and Invariant Subspaces
3.6.4 Subspaces of irrational functions: dipole-type solutions
The origin of such subspaces and exact solutions is the quadratic PME
u
t
= F[u] ≡ (u
2
)
xx
in IR × IR
+
, (3.145)
possessing the self-similar dipole Barenblatt–Zel’dovich solution [28]
u(x , t) = t
−
5
8
x
1
2
1
12
A − t
−
3
8
x
3
2
+
for x ≥ 0 (A > 0), (3.146)
which is extended for x < 0 as an odd function. The solution has the fixed point at
x = 0, where u(0, t) ≡ 0, and the graph of u(x , t) has a typical dipole form in x.The
corresponding initial function at t = 0 is proportional to δ
(x ), the weak derivative
of Dirac’s delta. Actually, this is a solution on the subspace
W
2
= L
x
1
2
, x
2
that is invariant under the quadratic operator F in (3.145). At the same time, it is a
standard similarity solution induced by a group of scaling transformations.
Let us show that such subspaces and solutions exist for higher-order parabolic
PDEs. Consider the 2mth-order quadratic operator
F[u] = (−1)
m+1
D
2m
x
u
2
. (3.147)
Proposition 3.29
Operator
(3.147)
preserves the
(m+1)
-dimensional subspace
W
m+1
= L
x
1
2
, x
3
2
, ..., x
2m−3
2
, x
2m−1
2
, x
2m
.
Proof. It follows that, for any u ∈ W
m+1
,
u
2
∈ L
x, x
2
, ..., x
2m−1
, x
2m+
1
2
, ..., x
2m+
2m−1
2
, x
4m
,
which yields D
2m
x
(u
2
) ∈ W
m+1
.
Example 3.30 The fourth-order equation
u
t
=−(u
2
)
xxxx
is parabolic in the positivity domain {u > 0}. The corresponding solutions are
u(x , t) = C
1
(t)x
1
2
+ C
2
(t)x
3
2
+ C
3
(t)x
4
∈ W
3
for t ≥ 0,
C
1
=−
945
8
C
1
C
3
,
C
2
=−
3465
8
C
2
C
3
,
C
3
=−1680C
2
3
.
Solving the DS yields the explicit formula
u(x , t) =
At
−
9
128
x
1
2
+ Bt
−
33
128
x
3
2
+
1
1680t
x
4
+
. (3.148)
For different values of A and B, (3.148) describes a dipole-like singularity at t = 0,
extinction/quenching phenomena, and the interface propagation. A proper setting of
the corresponding Stefan–Florin FBP with positive solutions can be also revealed.
© 2007 by Taylor & Francis Group, LLC
3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 139
3.6.5 Trigonometric subspace
A typical example is the following TFE with source possessing blow-up solutions:
u
t
= F[u] ≡ (−1)
m+1
D
x
uD
2m−1
x
u
+ 2u
2
. (3.149)
Proposition 3.31
Operator
F
in
(3.149)
admits
W
3
= L{1, cos x , sin x}
.
Equation (3.149) on W
3
is a third-order DS that describes blow-up of 2π-periodic
solutions. As shown in Example 3.17, the 2D restrictions L{1, cos x } and L{1, sin x}
are also invariant and generate simpler DSs on which blow-up similarity solutions
are asymptotically stable.
3.7 Oscillatory, changing sign behavior in the Cauchy problem
For a moment we digress from invariant subspaces for TFEs and discuss some as-
pects concerning general solutions of changing sign of the Cauchy problem.
Source-type solutions of the TFE. Consider the signed 2mth-order TFE with the
higher-order term only,
u
t
= (−1)
m+1
D
x
|u|
n
D
2m−1
x
u
in IR × IR
+
, (3.150)
where n > 0 is a parameter. The fundamental source-type solution has the similarity
form
b(x, t) = t
−β
g(ξ), ξ =
x
t
β
, where β =
1
n+2m
and, on integration once, g solves the (2m − 1)th-order ODE
(−1)
m+1
|g|
n
g
(2m−1)
+ βgξ = 0inIR . (3.151)
The unit mass condition is also imposed
g(ξ) dξ = 1 (3.152)
and can always be achieved by scaling. Another usual normalization condition is
g(0) = 1 that will be used sometimes later on. For the Cauchy problem, we are
looking for solutions of the maximal regularity, which can be admitted by the ODE
(3.151). We pose m − 1 symmetry boundary conditions at the origin,
g
(0) = g
(0) = ... = g
(2m−3)
(0) = 0 (g(0)>0). (3.153)
For m = 2, rigorous mathematical results on existence and uniqueness for the prob-
lem (3.151), (3.152) are known for n ∈ (0, 1]; see [174] where Bernis–McLeod
approach [47] was used. For other n and m ≥ 3, we rely on analytic-numerical
evidence to be presented.
Let g be supportedon the interval [−ξ
0
,ξ
0
]. We can also usenormalization ξ
0
= 1
instead of (3.152). At the right-hand interface, for ξ ≈ ξ
−
0
, we then introduce the
oscillatory component ϕ by
g(ξ) = (ξ
0
− ξ)
γ
ϕ(s), s = ln(ξ
0
− ξ), where γ =
2m−1
n
. (3.154)
Setting
ξ = ξ
0
− e
s
for s &−1
© 2007 by Taylor & Francis Group, LLC

140 Exact Solutions and Invariant Subspaces
and omitting the exponentially small non-autonomous perturbation yields that ϕ(s)
satisfies
P
2m−1
[ϕ] = c
0
|ϕ|
−n
ϕ in IR , where c
0
= βξ
0
(−1)
m+1
. (3.155)
Here, {P
k
[ϕ], k ≥ 0} denote operators that are constructed by the iteration
P
k+1
[ϕ] = (P
k
[ϕ])
+ (γ − k)P
k
[ϕ]fork = 0, 1, ... , P
0
[ϕ] = ϕ. (3.156)
For instance, for m = 2
γ =
3
n
and m = 3
γ =
5
n
, respectively,
P
3
[ϕ] = ϕ
+ 3(γ − 1)ϕ
+ (3γ
2
− 6γ + 2)ϕ
+γ(γ − 1)(γ − 2)ϕ and
P
5
[ϕ] = ϕ
(5)
+ 5(γ − 2)ϕ
(4)
+ 5(2γ
2
− 8γ + 7)ϕ
+5(γ − 2)(2γ
2
− 8γ + 5)ϕ
+ (5γ
4
− 40γ
3
+ 105γ
2
−100γ + 24)ϕ
+ γ(γ − 1)(γ − 2)(γ − 3)(γ − 4)ϕ.
(3.157)
Traveling waves. For TWs u(x , t) = f (y), with y = x − λt, the ODE is easier
(−1)
m+1
| f |
n
f
(2m−1)
+ λ f = 0fory > 0, f (0) = 0, (3.158)
where the left-hand interface is at y = 0. The oscillatory component is given by
f (y) = y
γ
ϕ(s), s = ln y, where γ =
2m−1
n
, (3.159)
where ϕ solves the ODE (3.155) with c
0
= (−1)
m
λ.
As before, we are mainly interested in periodic solutions ϕ(s) of ODEs (3.155),
which, according to (3.154), determine typical (and sometimes generic) oscillatory
behavior of solutions near interfaces, as shown in Figure 3.5(a). Existence and mul-
tiplicity of periodic solutionsof dynamical systems in IR
n
is a classical area of appli-
cations of topologicaland geometric methods of nonlinear analysis, such as rotations
of vector fields and index-degreetheory; see Krasnosel’skii–Zabreiko[355, Sect. 13,
14]. Another mathematical direction is classical branching theory; see Vainberg–
Trenogin [565, Ch. 6]. In our case, an n-branching approach may be effective, since
for n = 0, the unique solution of the problem (3.151), (3.152) is indeed the rescaled
kernel of the fundamental solution. A mathematical justification of such a branching
is a hard
OPEN PROBLEM. We also refer to [569, 399, 336] as a guide to modern
theory of periodic solutions of higher-order nonlinear ODEs. In general, for large
m, equations (3.155) are difficult to study, and especially as the main concern is the
number of their different periodic solutions, as well as the identification of the most
stable solution that describes a general structure and complexity of multiple zeros of
solutions near interfaces. We will also rely on careful numerical evidence on exis-
tence, uniqueness and stability of periodic solutions. It is natural to begin recalling
the properties of the linear PDE (3.150) with n = 0, which explain the oscillatory
patterns in the quasilinear case for small n > 0.
Oscillations in the linear equations. For n = 0 in (3.150), the linear polyharmonic
PDE is obtained,
u
t
= (−1)
m+1
D
2m
x
u in IR × IR
+
,
© 2007 by Taylor & Francis Group, LLC
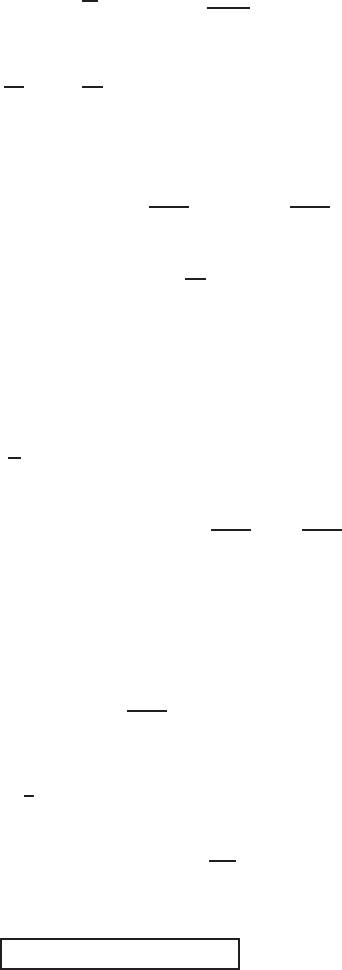
3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 141
whose oscillatory properties are described by its fundamental solution
b(x, t) = t
−
1
2m
g(ξ), ξ =
x
t
1/2m
, (3.160)
where g is the unique exponentially decaying solution of the ODE
(−1)
m+1
g
(2m)
+
1
2m
g
ξ +
1
2m
g = 0inIR ,
g = 1. (3.161)
See Eidelman’s classic book [164, Ch. 1] for the existence and sharp estimates of
fundamental solutions of higher-order linear parabolic operators. By substituting, it
is not hard to check that the behavior as ξ →+∞of solutions of (3.161) is given by
g(ξ) ∼ ξ
−µ
e
aξ
α
, with α =
2m
2m−1
and µ =
m−1
2m−1
, (3.162)
where a is the root with the maximal Rea < 0 of the characteristic equation
(−1)
m
(αa)
2m−1
=
1
2m
. (3.163)
Estimating the number of complex conjugate pairs of roots, a, and their real parts
yields the following useful conclusion.
Proposition 3.32 (i)
The asymptotic representation
(3.162)
of the rescaled kernel
g(ξ)
of the fundamental solution
(3.160)
can be represented in terms of a quasi-
periodic function containing not more than
([·]
denotes the integer part
)
m
2
fundamental frequencies.
(3.164)
(ii)
There exists a constant
D > 0
such that
|g(ξ)|≤De
−d|ξ|
α
in
IR ,
where
d =
2m−1
(2m)
α
cos
mπ
2m−1
.
It follows from (3.164) that the total asymptotic linear bundle of exponentially
decaying solutions (3.162) satisfies
the bundle is m-dimensional. (3.165)
For m odd, this includes the 1D non-oscillatory bundle, corresponding to the real
negative root of (3.163)
a
0
=−
2m−1
(2m)
α
.
Oscillatory periodic patterns for m = 2 and a heteroclinic bifurcation. Let us
begin with the simplest case, m = 2, where the third-order ODE (3.155) takes the
form (here c
0
=−1andγ =
3
n
)
P
3
[ϕ] ≡ ϕ
+ 3(γ − 1)ϕ
+ (3γ
2
− 6γ + 2)ϕ
+γ(γ − 1)(γ − 2)ϕ =−
ϕ
|ϕ|
n
.
(3.166)
Numerical experiments (Figure 3.6) show that (3.166) admits a unique stable peri-
odic solution for all n ∈ (0, n
h
),where
n
h
= 1.758665... (m = 2)
is a critical heteroclinic bifurcation exponent.
The exponent n
h
plays an important role and shows the precise parameter range
© 2007 by Taylor & Francis Group, LLC

142 Exact Solutions and Invariant Subspaces
0 2 4 6 8 10
−0.025
−0.02
−0.015
−0.01
−0.005
0
0.005
0.01
0.015
0.02
0.025
s
φ(s)
(a) n = 1
0 5 10 15 20 25 30 35 40
−0.5
−0.4
−0.3
−0.2
−0.1
0
0.1
0.2
0.3
0.4
0.5
s
φ(s)
(b) n =
3
2
Figure 3.6 Stable periodic behavior of (3.166), m = 2, for n = 1 (a) and n =
3
2
(b).
of n for which all the ODE profiles near interfaces are oscillatory (this may also be
key for the corresponding PDE). Numerical results reveal a non-local heteroclinic
bifurcation at n = n
h
associated with two unstable equilibria of (3.166)
ϕ
±
=±
−
1
γ(γ−1)(γ −2)
1
n
for n ∈
3
2
, 3
.
Note that (3.159) with ϕ(s) ≡ ϕ
+
yields a non-oscillatory behavior; see the dashed
line in Figure 3.5(a). Figure 3.7 shows a typical “heteroclinic” deformation of peri-
odic patterns as n → n
−
h
, where, in order to reveal the widest periodic pattern (the
bold line), we need to take n = 1.758664976837300 (where not all the 15 decimals
are reliable). This is a standard scenario of homoclinic-heteroclinic bifurcations of
periodic solutions in ODEs; see Perko [460, Ch. 4]. A rigorous justification of such
bifurcations is difficult and is an
OPEN PROBLEM, especially for higher-order equa-
tions with m = 4, 6, ... to be considered below.
For n > n
h
, the behavior of solutions of the ODE (3.166) becomes exponentially
unstable and oscillatory or changing sign patterns are not observed. It is likely that
precisely above n = n
h
, the ODE (and, to some extent, the correspondingPDE) loses
its natural similarities with the linear equation for n = 0, i.e., some local properties
of solutions dramatically change at n = n
h
.
m ≥ 3: unstable periodic behavior for odd m and stable for even. In numerical
experiments, we have observed a single stable oscillatory behavior for even m ≥ 2
and an unstableorbitfor odd m. Figure 3.8(a) showssolutionsof the ODE (3.155)for
m = 3 and stability of equilibria ϕ
±
. In this case, the unstable periodic solution lies
in between those two stable flows of orbits tending to ϕ
+
and ϕ
−
as (b) explains. It
turns out that such an unstable periodic solution exists until the “heteroclinic” value
ˆn
h
= 1.909... (m = 3).
In view of its unstability, the corresponding analytical and numerical techniques be-
come more involved; see [175] for extra details.
For m = 4, i.e., for the eighth-order TFE, the solutions ϕ(s) approach a stable
periodic pattern; see Figure 3.9. The periodic solution is easily detected above the
© 2007 by Taylor & Francis Group, LLC
