Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics
Подождите немного. Документ загружается.


3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 113
self-adjoint operators are difficult. Let us determine the point spectrum of the special
extension. Notice first that solutions of the eigenvalue equation
Bψ = λψ
exhibit the following generic exponential growth near the infinite singular point:
ψ(η) ∼ e
µη
as η →+∞, with µ = (2a
0
)
−
1
3
1
2
± i
√
3
2
.
Therefore, a proper functional setting for B involves the weighted space L
2
ρ
with
the exponential weight ρ(η) = e
−bη
, where b ∈
0,
1
2
(2a
0
)
−1/3
is a constant. It
turns out that B possesses the real point spectrum in spaces of functions that are
sufficiently smooth at η = 0 (e.g., such as H
4
ρ
),
σ
p
(B) =
λ
k
=−
k
2
+ 2, k = 0, 1, 2, ...
,
and each eigenfunction ψ
k
(η) is a kth-degree polynomial
ψ
k
(η) = b
k
η
k
+
2k(k−1)(k−2)
2
3
a
0
η
k−1
+ ...
,
where b
k
are some normalization constants. In a proper setting, the resolvent of
B is compact in L
2
ρ
(see Remarks for extra details), so the whole spectrum σ(B)
can be made discrete. These polynomials are complete and closed in L
2
ρ
(IR );see
Kolmogorov–Fomin [352, p. 431]. So, studying (3.51), eigenfunction expansions
can be used. To this end, let us introduce the adjoint operator
B
∗
v =−a
0
(ηv
)
+
1
2
v
η +
5
2
v
with the same spectrum and find the bi-orthogonal(in L
2
(IR ))set{ψ
∗
k
}of eigenfunc-
tions satisfying, after normalization, (ψ
i
,ψ
∗
j
)=δ
ij
. Then, in L
2
ρ
, we can look for
solutions of (3.51) in the form of
w(η,τ) =
(k≥0)
c
k
(τ )ψ
k
(η), where c
k
(τ ) =(w(·,τ),ψ
∗
k
),
and study the DS for the expansioncoefficients {c
k
(τ )} that describes the asymptotic
behavior. It follows that the turning patterns satisfying the rescaled equation (3.51)
correspond to the evolution on the stable and center manifolds that are tangent to
the corresponding subspaces of B, i.e., as τ →∞, w(η, τ) ∼ e
λ
k
τ
ψ
k
(η), with
λ
k
∈ σ
p
(B) for some k ≥ 4, so λ
k
≤ 0. In particular, according to the scaling (3.50),
taking k = 4 with λ
4
= 0 gives the asymptotic behavior for the first turning pattern
(most probably, generic)
Y (y, t) ∼ e
−2τ
ψ
4
(η) + ... , where ψ
4
(η) = b
4
η
4
+ 32a
0
η
is the corresponding eigenfunction. This determines the behavior on sets defined
as y = O(
√
t
0
− t) to be matched with the behavior (3.47) on smaller sets in the
variable ζ in (3.46), i.e., for y = O(t
0
− t), to get a global structure of this first
turning pattern. A rigorous justification of such asymptotic and matching analysis is
OPEN for higher-order TFEs. The exact solutions remain the only tool to test such a
curious singularity formation phenomenon.
© 2007 by Taylor & Francis Group, LLC
114 Exact Solutions and Invariant Subspaces
u(x , t)
t = 1
s
+
(t)
s
−
(t)
x
t > 1
t < 1
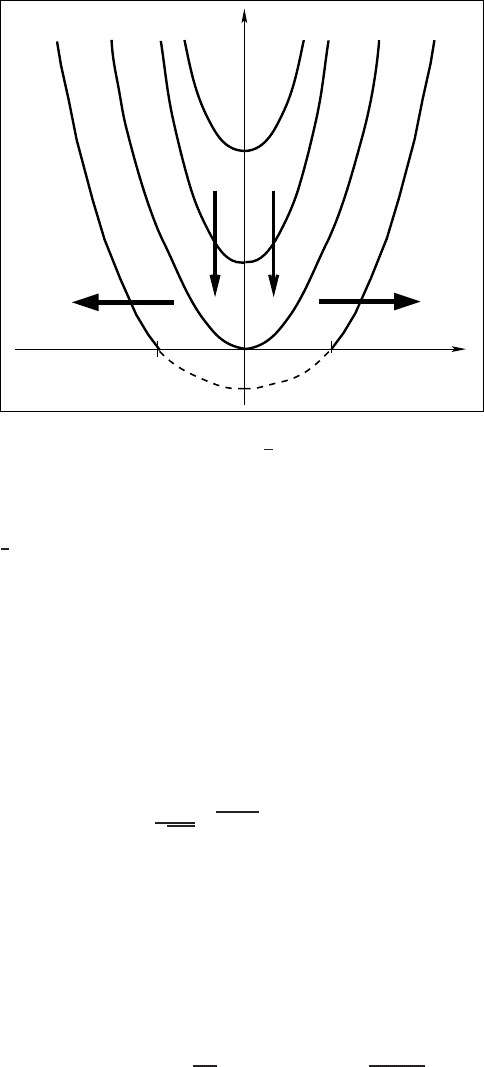
0
Figure 3.2 The exact solution (3.29) with A
0
=
5
6
, E
0
< 0: (i) quenching at t = 1, and (ii)
two interfaces appear for t > 1.
3.2.6 Quenching patterns
Take A
0
=
5
6
again,and now fixanarbitraryE
0
≥ 0 in (3.29), giving the single point
quenching, where the strictly positive solution first touches the singularity zero level
{u = 0}at t = 1, as shown in Figure 3.2. If E
0
< 0 for the asymptotic description of
quenching,we still can use the same rescaled variables(3.39)to observeconvergence
(3.41), where the self-similar profile is now strictly positive,
g(ξ) = 1 +|E
0
|ξ
2
.
The asymptotic quenching phenomenon is described by the same rescaled equation
(3.44) with, plausibly, a generic stabilization to the similarity profile; proof is an
OPEN PROBLEM. After quenching, for t > 1, two interfaces appear with the non-
Lipschitz behavior
s
±
(t) =±
1
√
|E
0
|
√
t − 1 + ... as t → 1
+
, (3.53)
so that a smooth flow, corresponding to the uniformly parabolic TFE for t < 1, is re-
placed by the FBP for the degenerate equation for t > 1, with a quenching transition
at t = 1
−
. In general, the questions of solution extensions beyond singular quench-
ing remain
OPEN. For similar second-orderequations,such as (3.36), this determines
extensions of order-preserving semigroups for various types of singularities, [226,
Sect. 6.2].
A different quenching pattern occurs for E
0
= 0 in (3.29), and a distinct spatial
rescaled variable η is necessary for describing the limit t → 1
−
,
e
τ
u(x , t) → 1 +
1
120
η
2
, where η =
x
(1−t )
1/4
. (3.54)
© 2007 by Taylor & Francis Group, LLC

3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 115
Then we introduce another rescaled function, v(η,τ) = e
τ
u(x , t),thatisdefined
according to (3.54) and satisfies the following equation:
v
τ
=−
1
4
v
η
η + v − 1 − e
−τ
(vv
ηηη
)
η
. (3.55)
Unlike the rescaled parabolic PDE (3.44), the thin film operator now reduces to a
fourth-orderperturbationthat is exponentiallysmallas τ →∞.Thisgivesasingular
perturbation problem for the linear autonomous Hamilton–Jacobi equation
v
τ
=−
1
4
v
η
η + v − 1. (3.56)
The convergence as τ →∞of some classes of solutions of (3.55) and (3.56) rep-
resents an interesting
OPEN PROBLEM; though such behavior is not expected to be
generic, unlike the above similarity with E
0
< 0. For PMEs with absorption (3.36)
for which, in (3.55),the fourth-orderoperatoris replaced by the diffusionone (vv
η
)
η
,
such behavior is proved to be stable; see results in [245, Ch. 5].
After quenching at t = 1, the interfaces also exhibit a different behavior (cf.
(3.53))
s
±
(t) =±
120(t − 1)
1
4
+ ... as t → 1
+
.
We expect that it is not generic and corresponds to very flat initial data u(x, 1
−
)
created by such a peculiar unstable quenching.
3.2.7 On extinction patterns with zero contact angle, the Cauchy problem
In the case of the standard FBP having conditions as in (3.14), it seems that the
present TFE with absorption does not possess exact solutions on invariant subspaces
(for other parameters,such solutionsdo exist;see Example 3.10 below).On the other
hand, self-similar solutions of the form (3.42) may be introduced, where g(ξ) is an
even positivesolution of the ODE (3.43) on some interval ξ ∈ (0,ξ
0
) with conditions
g(ξ
0
) = g
(ξ
0
) = (gg
)(ξ
0
) = 0, and g
(0) = g
(0) = 0, (3.57)
correspondingto thesymmetry attheoriginξ = 0. The behaviorclose to theinterface
at ξ = ξ
0
is
g(ξ) = (ξ
0
− ξ)
2
√
2|ln(ξ
0
− ξ)|+C + ... (C ∈ IR ).
Existence (or nonexistence) of such g(ξ ) leads to two-parameter, {ξ
0
, C}, shooting
to satisfy two symmetry conditions at ξ = 0andremainsan
OPEN PROBLEM.
In the Cauchy problem for such degenerate PDEs to be discussed systematically
later on, solutions typically are of changing sign, so the PDE and the similarity ODE
are modified as follows:
u
t
=−(|u|u
xxx
)
x
− signu ⇒ −(|g|g
)
−
1
2
g
ξ + g − sign g = 0. (3.58)
Then, (3.57) are also valid at interfaces, but the solutions g(ξ ) are smoother and are
oscillatory with a different behavior (corresponding to (|g|g
)
+ sign g = 0)
g(ξ) = (ξ
0
− ξ)
2
ϕ(s), s = ln(ξ
0
− ξ), as ξ → ξ
−
0
,
where the oscillatory component ϕ(s) is a periodic solution of a nonlinear ODE.
© 2007 by Taylor & Francis Group, LLC
116 Exact Solutions and Invariant Subspaces
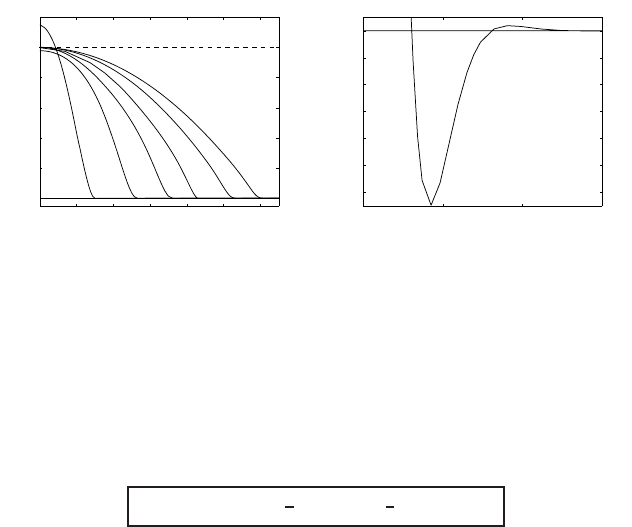
0 2 4 6 8 10 12
0
0.2
0.4
0.6
0.8
1
ξ
g(ξ)
(a) six profiles
5 5.5 6 6.5
−12
−10
−8
−6
−4
−2
0
x 10
−4
ξ
g(ξ)
(b) oscillations, enlarged
Figure 3.3 Similarity extinction profiles satisfying the ODE (3.58) with the conditions (3.57);
six profiles (a) and oscillations near the interface for the second profile (b).
Details will be presented in Section 3.7. Figure 3.3(a) shows six similarity profiles
for ξ>0. In (b), these numerical results reveal the oscillatory character of solutions
near interfaces, an intriguing part of our future analysis.
Example 3.6 (TFE with cubic operator) Take the unique operator from Proposi-
tion 3.5(ii) and consider the TFE with constant absorption
u
t
=−
u
2
u
xxx
−
3
2
uu
x
u
xx
+
3
4
(u
x
)
3
x
− 1.
Taking the subspace of even fourth degree polynomials yields solutions
u(x , t) = C
1
(t) + C
2
(t)x
2
+ C
3
(t)x
4
,
C
1
= 3C
1
C
2
2
− 24C
2
1
C
3
− 1,
C
2
=−9(C
2
2
+ 2C
1
C
3
)C
2
,
C
3
= 30(4C
1
C
3
− C
2
2
)C
3
.
This DS is more difficult and explicit solutions do not exist. A simpler system occurs
by setting C
2
(t) ≡ 0, which corresponds to the subspace W
2
= L{1, x
4
}, but it is
not clear whether the resulting extinction behavior is generic. The asymptotics of
extinction as t → T
−
is easy to detect, since, on any bounded orbit of the above DS,
C
1
(t) = T − t + O
(T − t)
2
,
while C
2,3
(t) remainalmostconstantfor t ≈ T . This givesthe necessaryasymptotics
of the extinction (or quenching for positive solutions) behavior. The corresponding
rescaled equations can be formulated in a similar fashion. Other features of the FBPs
can also be described, though some of the computations are not explicit or easy.
3.2.8 Quartic operators: applications to extinction and blow-up
As a new application, consider the fourth-order TFE with source or absorption
v
t
=−
v
n
v
xxx
x
+ g(v). (3.59)
© 2007 by Taylor & Francis Group, LLC

3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 117
Introducing the new independent variable
v = u
µ
, where µ =
3
n
, (3.60)
splits the thin film operator into five primitive monomials of the algebraic homoge-
nuity four,
u
t
=−
u
3
u
xxxx
+ (4µ − 1)u
2
u
x
u
xxx
+3(µ − 1)u
2
(u
xx
)
2
+ 3(µ − 1)(2µ − 1)u(u
x
)
2
u
xx
+µ(µ − 1)(µ − 2)(u
x
)
4
+
n
3
u
1−µ
g(u
µ
).
(3.61)
Assume that the last zero-order term is a linear function, i.e.,
n
3
u
1−µ
g(u
µ
) = a + bu. (3.62)
Then polynomial subspaces will depend on the differentialoperatorin (3.61). Firstly,
this admits the trivial subspace of linear functions W
2
= L{1, x}, which does not
provide us with interesting solutions. In particular, these are traveling waves that are
unbounded as x →∞. We are interested in solutions of typical bell-shaped forms
localized on a bounded interval in x. Secondly, extensions of W
2
are possible in the
following cases:
Proposition 3.7
The operatorgivenin
(3.61)
and
(3.62)
preserves
W
3
= L{1, x , x
2
}
iff
n = 3
,
n = 6
,or
n =−2
.
Proof. Plugging u = C
1
+C
2
x +C
3
x
2
∈ W
3
into the quartic operator yields that the
terms on L{x
3
, x
4
} vanish iff
4(µ − 1)[3 + 6(2µ − 1) + 4µ(µ − 2)] = 0,
which yields either µ = 1or4µ
2
+ 4µ − 3 = 0, i.e., µ =
1
2
or µ =−
3
2
.
Example 3.8 (Extinction behavior) Let us choose a =−1andb = 0 in (3.62),
giving a constant absorption term in (3.61).
Case n = 3(µ = 1). This is quite simple, since the resulting PDE
u
t
= F
4
[u] − 1 ≡−u
3
u
xxxx
− 3u
2
u
x
u
xxx
− 1 (3.63)
does not contain lower differential terms, so that, being restricted to W
3
, it is equiv-
alent to the linear ODE
u
t
=−1. (3.64)
Curiously, this trivial evolution on W
3
describes the actual general phenomenon of
asymptoticdegeneracyof the PDEs near extinction.To show this, consider nonnega-
tive and even in x (symmetric)solutionson W
2
= L{1, x
2
}. Noticingthat the general
solution of (3.64) is
u(x , t) = h(x) − t,
where h(x ) is arbitrary(initial data), we choose the parabolicprofile h(x ) = T −dx
2
with positive constants T and d. Next, bearing in mind the FBP, take the positive part
to obtain the following pattern near the extinction time T :
u(x , t) =
T − t − dx
2
+
≡ (T − t)g(ξ) = (T − t)
1 − d ξ
2
+
, (3.65)
© 2007 by Taylor & Francis Group, LLC

118 Exact Solutions and Invariant Subspaces
where ξ denotes the spatial rescaled variable x/
√
T − t. For general even bell-
shaped solutions of (3.63), this asymptotic behavior on W
2
suggests introducing the
rescaled solution
u(x , t) = (T − t)w(ξ, τ ), τ =−ln(T − t), (3.66)
satisfying a typical singular (exponentially) perturbed equation,
w
τ
=−
1
2
w
ξ
ξ +w −1 +e
−2τ
F
4
[w]. (3.67)
Such PDEs occurred before for a number of the TFEs with absorption. Therefore,
we expect that, as τ →∞, bounded orbits {w(·,τ)} converge to stationary profiles
g, solving the linear ODE
−
1
2
g
ξ + g − 1 = 0,
that gives precisely the parabolic profiles g(ξ ) in (3.65). In this sense, solutions on
the invariant subspace can detect the correct generic asymptotic behavior of extinc-
tion. As usual, a rigorous passage to the limit in (3.67) represents a difficult
OPEN
PROBLEM
.
Case n = 6(µ =
1
2
). In this case, the diffusion-absorption equation takes the form
u
t
=−
u
3
u
xxxx
+ u
2
u
x
u
xxx
−
3
2
u
2
(u
xx
)
2
+
3
8
(u
x
)
4
− 1.
We have the following exact symmetric solutions on W
2
:
u(x , t) =
C
1
(t) + C
3
(t)x
2
+
, (3.68)
C
1
= 6C
2
1
C
2
3
− 1,
C
3
= 12C
1
C
3
3
.
We cannot solve the system explicitly and will compute the generic asymptotic be-
havior of orbits near the extinction time, as t → T
−
. This yields C
1
(t) = T −t +...
and C
3
(t) →−d < 0, so that the behavior (3.65) remains valid asymptotically.
Using the same rescaled variables (3.66) makes it possible to formulate the corre-
sponding singular perturbed problem (3.67) for which the exact solutions on W
3
are
expected to describe the generic asymptotic behavior. This is an
OPEN PROBLEM.
Example 3.9 (Blow-up) Case n =−2(µ =−
3
2
). In (3.59), we take
g(v) =−
3
2
av
5
3
−
3
2
bv,
so, again choosing a =−1andb = 0 yields the TFE with source
v
t
=−
1
v
2
v
xxx
x
+
3
2
v
5
3
. (3.69)
The reaction term ∼ v
5/3
is superlinear for v 1, so that blow-up is guaranteed for
solutions of (3.69) with sufficiently large positive initial data v
0
(x ).
Setting v = u
−3/2
yields quartic nonlinearities in the PDE
u
t
=−
u
3
u
xxxx
− 7u
2
u
x
u
xxx
−
15
2
u
2
(u
xx
)
2
+30u(u
x
)
2
u
xx
−
105
8
(u
x
)
4
− 1.
(3.70)
© 2007 by Taylor & Francis Group, LLC
3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 119
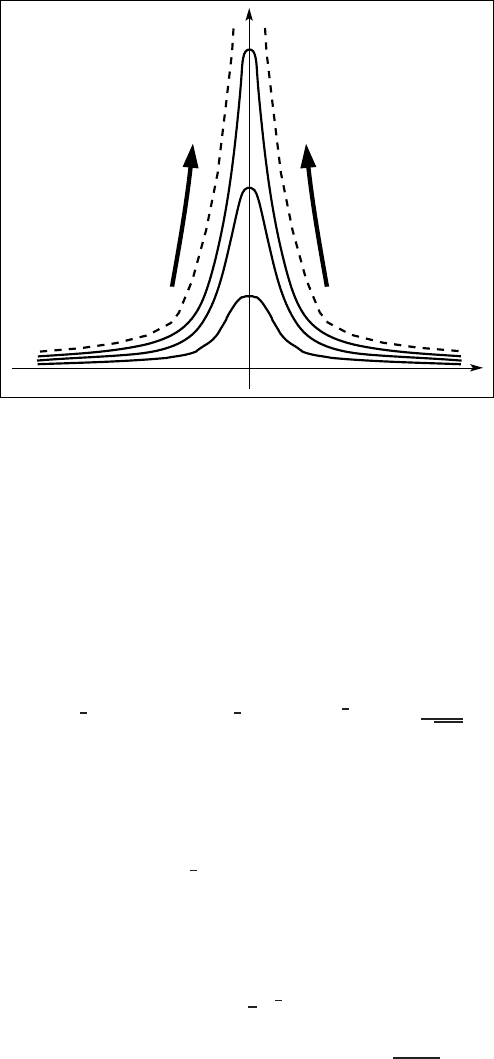
v(x , t)
v(x , T
−
)
final-time profile
x
t
1
< t
2
< t
3
< T
0
t
1
t
2
t
3
Figure 3.4 Single point blow-up described by positive exact solutions of (3.69) on W
3
.
The blow-up behavior for (3.69) is equivalent to the quenching for (3.70). We look
for nonnegativesolutions (3.68) and obtain the DS for expansion coefficients
C
1
= 30C
2
1
C
2
3
− 1,
C
3
=−180C
1
C
3
3
.
Let T > 0bethefinite quenching time of a fixed bounded orbit. Then the DS gives
as t → T
−
the behavior C
1
(t) = T − t + ... and C
3
(t) → d > 0. This yields the
blow-up behavior on W
3
,ast → T
−
,
v(x , t) = u
−
3
2
(x , t) ≈ (T − t)
−
3
2
1 + d ξ
2
−
3
2
,ξ=
x
√
T −t
. (3.71)
These exact solutions are strictly positive,so that these are classical smooth solutions
of the TFE (3.69) on IR × (0, T ).
The blow-up evolution is shown in Figure 3.4. By (3.71), there occurs the single
point blow-up as x = 0 only. Letting t → T
−
yields the final-time profile
v(x , T
−
) = d
−
3
2
|x|
−3
(1 + o(1)) for x ≈ 0.
As shown in the previous example, these exact solutions asymptotically converge as
t → T
−
to the sufficiently smooth profiles given by the ODE u
t
=−1. This implies
that the blow-up patterns (3.71) are described as t → T
−
by the ODE
v
t
=
3
2
v
5
3
.
This is easily seen from the equations (3.69),written for the rescaledfunction v(x, t) =
(T −t)
−3/2
w(ξ, τ) with the same spatial rescaling ξ = x/
√
T − t. The equation for
© 2007 by Taylor & Francis Group, LLC

120 Exact Solutions and Invariant Subspaces
w contains a singular exponentially small perturbation as τ →∞,
w
τ
=−
1
2
w
ξ
ξ −
3
2
w +
3
2
w
5
3
− e
−2τ
w
−2
w
ξξξ
ξ
.
The phenomenon of such an asymptotic degeneracy of these TFEs near blow-up is
an
OPEN PROBLEM.
3.3 Exact solutions with zero contact angle
Let us return to exact solutions satisfying the more physically meaningful zero con-
tact angleconditionin (3.14).We again beginby studyingthe extinctionphenomenon
for the TFE with absorption, which is as a manifestation of an “evaporation” thin film
phenomenon; see Section 3.2.
Example 3.10 (Singularities and interfaces) We consider the TFE with a strong
non-Lipschitz absorption term,
v
t
=−(vv
xxx
)
x
−
√
v, (3.72)
and now impose the zero contact angle condition, so, at each interface,
v = v
x
= vv
xxx
= 0atx = s(t). (3.73)
Setting v = u
2
yields an equation with the cubic operator,
u
t
=−
1
2
u(u
2
)
xxxx
− u
x
(u
2
)
xxx
−
1
2
≡ F
3
[u] −
1
2
, (3.74)
exhibiting the following invariant property.
Proposition 3.11
Operator
F
3
in
(3.74)
admits the subspace
W
3
= L{1, x , x
2
}
.
Taking u = C
1
+ C
2
x + C
3
x
2
yields
F
3
[u] =−12(C
1
C
3
+ C
2
2
)C
3
− 60C
2
C
2
3
x − 60C
3
3
x
2
∈ W
3
. (3.75)
For simplicity, setting C
2
(t) ≡ 0 (meaning even and symmetric in x patterns) gives
the following solutions of the original PDE (3.72) on W
2
= L{1, x
2
}:
v(x , t) = u
2
(x , t) ≡
C
1
(t) + C
3
(t)x
2
2
+
, (3.76)
which, clearly, satisfy all three free-boundary conditions (3.73). In this case, (3.75)
implies
C
1
=−12C
1
C
2
3
−
1
2
,
C
3
=−60C
3
3
.
(3.77)
The last ODE is solved,
C
3
(t) =±
1
√
120
1
√
t
for t > 0, (3.78)
and, from the first,
C
1
(t) = A
0
t
−
1
10
−
5
11
t, where A
0
= constant. (3.79)
© 2007 by Taylor & Francis Group, LLC
3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 121
Quenching and dynamic interface equation. Consider first the plus sign in (3.78),
where, for convenience, setting A
0
=
5
11
in (3.79) yields
u(x , t) =
5
11
t
−
1
10
1 − t
11
10
+
1
√
120
1
√
t
x
2
+
. (3.80)
This solution is strictly positive for all t ∈ (0, 1), and vanishes for the first time at
t = 1 at the point x = 0 that describesthe quenching phenomenon. After quenching,
for t > 1, two interfaces x =±s(t) appear, where
s(t) = R(t) ≡
5
√
120
11
t
2
5
t
11
10
− 1
. (3.81)
At the initial moment of time t = 1
+
, the interface is not Lipschitz continuous,
s(t) = (30)
1
4
√
t − 1 + ... ,
andthis poses a problemof a post quenchingbehaviorof the extensionof the solution
after this evolution singularity occurred at t = 1.
In order to derive the regularity interface equation, we use the same elementary
formulae (3.31) and calculate u
t
from (3.74) for the solution (3.80). We obtain the
following two-term expression:
s
= S[u] ≡ 6u
x
u
xx
+
1
2u
x
at x = s(t) for t > 1. (3.82)
Recall that, by construction, our solution already satisfies the necessary three free-
boundary conditions (3.73). Let us detect other interface equations by the time-
parameterization t =
1
30
1
(u
xx
)
2
that follows from (3.80). Then (3.81) yields
s
= R
(t) ≡ R
1
30
1
(u
xx
)
2
. (3.83)
This equation is again of the second order, but is different from (3.82). Equating the
right-hand sides of (3.82) and (3.83) yields a stationary second-order Neumann-type
free-boundary condition
6u
x
u
xx
+
1
2u
x
= R
1
30
1
(u
xx
)
2
at x = s(t) for t > 1.
Towards local well-posedness of the FBP. Let us present some arguments justify-
ing local existence/uniqueness of the FBP. We use the von Mises transformation by
introducing the dependent variable
X = X (u, t), so X (u(x, t), t) ≡ x, (3.84)
which is assumed to be well-defined in a neighborhood of the interface posed now
at u = 0, at least for sufficiently small t > 0. Initial data at t = 0aretakeninthe
bell-shaped form u
0
(x ) = [C
1
(0)+C
3
(0)x
2
]
+
, where C
1
(0)>0andC
3
(0)<0are
given constants, being initial data for the DS (3.77). This determines the unique so-
lution on the invariantsubspace with the known propertiesof extinction and singular
interfaces. In terms of the new function (3.84), initial data are smooth,
X
0
(u) =
C
1
(0)−u
|C
3
(0)|
for small u ≥ 0. (3.85)
Assuming that X (u, t) is strictly monotone decreasing at least for small u > 0, and
© 2007 by Taylor & Francis Group, LLC
122 Exact Solutions and Invariant Subspaces
calculating derivatives yields
u
t
=−
X
t
X
u
, u
x
=
1
X
u
, u
xx
=−
X
uu
(X
u
)
3
, u
xxx
=−
X
uuu
(X
u
)
4
+
3(X
uu
)
2
(X
u
)
5
, ... .
On substitution into (3.74), the following PDE for X is derived:
X
t
= H (X) ≡−u
2
X
uuuu
(X
u
)
4
−
10X
uu
X
uuu
(X
u
)
5
+
15(X
uu
)
3
(X
u
)
6
−u
6X
uuu
(X
u
)
4
−
21(X
uu
)
2
(X
u
)
5
−
6X
uu
(X
u
)
4
+
1
2
X
u
.
(3.86)
Consider the principal fourth-order term in (3.86). Firstly, it follows that we need
to deal with solutions satisfying X
u
(0, t) = 0(andfinite) at the origin to exclude
gradient singularities, so it we check that the initial function (3.85) satisfies this
inequality of transversality. Secondly, (3.86) is degenerated at the boundary point
u = 0, and the quadratic rate of degeneracy, O(u
2
), in the higher-order term makes
it possible to pose some standard boundary conditions at u = 0.
The actual construction of the solution is as follows. The following decomposition
of the solution is needed:
X =
ˆ
X +
˜
X, where
ˆ
X ∈ Span{1, u} and
˜
X = X −
ˆ
X. (3.87)
Projecting equation (3.86) onto
ˆ
W
2
= Span{1, u} yields the ODE–PDE system:
ˆ
X
t
=
ˆ
H(X),
˜
X
t
=
˜
H(X),
(3.88)
where
ˆ
H and
˜
H denote projections of H onto the correspondingsubspaces. The first
equation is a two-dimensional dynamical system, and the second equation is then a
parabolic PDE with the principal degenerate operator
B =−u
2
D
4
u
. (3.89)
This linear operator is symmetric in the weighted space L
2
ρ
((0,δ)), with a small
δ>0andρ = u
−2
. By classical theory of symmetric ordinary differential operators
(see Naimark [432]), estimating the solutions of the eigenvalue equation
Bψ =±iψ for u ≈ 0
gives four types of asymptotics ψ
1
(u) = O(1), ψ
2
(u) = O(u) (both contain loga-
rithmic factors in higher-order terms), ψ
3
(u) = O(u
2
),andψ
4
(u) = O(u
3
),where
ψ
3,4
∈ L
2
ρ
and ψ
1,2
∈ L
2
ρ
. Therefore, the deficiency indices of B are (2,2), so that,
any pair of self-adjoint Dirichlet boundary conditions at u = 1 gives a self-adjoint
extension. We need to take the unique Friedrichs self-adjoint extension of B with a
discrete spectrum, compact resolvent, and a complete, closed eigenfunction set. As
usual, this extension is induced by the Dirichlet conditions at the singular endpoint
u = 0, i.e., w(0) = w
(0) = 0 for functions from the domain D(B). According
to the representation (3.87), the parabolic problem for solutions
˜
X is well-posed,
provided that the transversality condition X
u
(0, t) = 0, as well as suitable (free-
boundary) conditions at u = 0, hold. Actually, the second equation in (3.88), after
dividing by u
2
, reduces to the PDE with the non-degenerate principal operator D
4
u
,
and the solution
˜
X ∈ D(B) can be constructed by eigenfunction expansion, where
© 2007 by Taylor & Francis Group, LLC
