Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics

Подождите немного. Документ загружается.

3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 123

the boundary conditions are key (see below). Note that, in view of analyticity of the

coefﬁcients of both equations, this gives a unique local analytic solution,

X (u, t) =



(k, j ≥0)

k, j

which can be constructed independently by substitution into (3.86) (convergence

needs special involved majorant-type estimates).

Thus free-boundary conditions are crucial for local existence of smooth solutions.

The dynamic interface equation (3.82) now reads

=−

)

at u = 0. (3.90)

Writing (3.86) in the form of

−u

uuuu

)

+ ... = X

)

−

in view of (3.90), the right-hand side is always zero at the boundary u = 0. It is

preciselythis that makes it possibleto constructa uniquelocal solution by semigroup

theory based on the spectral properties of the linear degenerate operator (3.89).

Hence, the initial-boundary value problem for (3.86) in a small neighborhood of

u = 0, t = 0 falls into the scope of the theory of higher-order parabolic PDEs; see

[164, 205, 550]. For simplicity, we impose a pair of standard Dirichlet or Neumann

boundary conditions at some ﬁxed point u = u

> 0, small enough where there are

no degeneracy and singularity. Once

X has been obtained, the DS for

X in (3.88)

gives the whole solution. The construction is local in u and t, and fails if extra de-

generacypoints appear in an arbitrarily small neighborhoodof the origin u = 0. This

would mean a new type of singularity which might affect the required regularity and

the interface equation.

Extinction: singular perturbation problem. The extinction phenomenon corre-

sponds to the minus sign in (3.78), so the explicit solution is

u(x , t) =



−



1 − t



−

√

120

√



. (3.91)

This solution has two interfaces for t ∈ (0, 1) that coincide at the extinction time

t = 1. The interface equations (3.82) or (3.83) remain the same. One can extract

from (3.91) the asymptotic extinction pattern as t → 1

−

u(x , t) = e

−τ



−

√

120



+ O



−2τ



, (3.92)

with rescaled variables y = x/

√

1 − t and τ =−ln(1 − t) →+∞. Therefore,

asymptoticextinctiontheory uses the rescaled function u(x, t) = e

−τ

w(y,τ),where

w satisﬁes a singular perturbed ﬁrst-order PDE,

=−

y + w −

+ e

−τ

[w]forτ  1. (3.93)

For general solutions, the passage to the limit τ →+∞in (3.93) and stabilization

to the stationary rescaled proﬁle g(y) =



−

√

120



given in (3.92) are difﬁ-

cult

OPEN PROBLEMS. Translating (3.92) to the original solution v(x, t) of the TFE

(3.72), on the invariant subspace W

, the following extinction behavior holds:

v(x , t) = (1 − t)



−

√

120

1−t



+ O(1 − t)



as t → 1

−

. (3.94)

124 Exact Solutions and Invariant Subspaces

On self-similar extinction behavior. In addition, the TFE (3.72) admits standard

similarity structures

(x , t) = (1 − t)

g(z), z =

(1−t )

3/4

, (3.95)

where, on substitution, g ≥ 0 solves the ODE

−(gg



)



−



z + 2g −

√

g = 0forz ∈ (0, z

g(z

) = g



) = (gg



)(z

) = 0, g



(0) = g



(0) = 0,

(3.96)

with free-boundary conditions at some z = z

> 0 and symmetry ones at the origin

z = 0. Then the ODE gives that, close to the interface,

g(z) = C(z

− z)

+ C

− z)

+ ... , with C > 0 and 12C

−

√

The space-time structure (3.95) is different from the behavior detected in (3.94) by

exact solutions on the invariant subspace. Comparing the rescaled variables y in

(3.92) and z in (3.95) yields that the self-similar extinction occurs on smaller sets

z = O(1),i.e.,

|x|∼(1 − t)

& (1 − t)

as t → 1

−

where the last sets are attributed to the rescaled variable y = x /

√

1 − t = O(1).

Unlike the above case of explicit solutions, the ODE (3.96) for zero contact angle

proﬁles g(z) is difﬁcult and existence/uniqueness(or nonexistence)are

OPEN PROB-

LEMS.

We claim that a stable (generic) extinction behavior is given by the exact solution

patterns, such as (3.94), so the asymptotic self-similar behavior given by (3.95) is

expected to be unstable. This is an

OPEN PROBLEM.

Oscillatory solutions of the Cauchy problem. The CP for the TFE with absorption

(3.72) demands another setting for solutions of changing sign. It is known that, for

n ∈





, generalized strong (i.e., sufﬁciently regular) solutions u(x, t) of the TFE

=−



|v|

xxx



in IR × IR

with bounded compactly supported initial data v

(x ) should be oscillatory near in-

terfaces in order to exhibit the maximal regularity. More precisely, such solutions

behave near the left-hand interface x = s(t) as

v(x , t) ∼ (x −s(t))

ϕ(ln(x − s(t))) as x → s

(t), (3.97)

where ϕ(s) denotes the oscillatory component and is typically a periodic changing

sign solution of a fourth-order ODE. Explanations are postponed until Section 3.7,

and here we discuss this phenomenon for the TFE with strong absorption (3.72).

First, in order to keep the parabolicity and absorption features, (3.72) is written as

=−(|v|v

xxx

)

−|v|

−

v in IR × IR

. (3.98)

Second, as usual, we ﬁrst detect the oscillatory component for the TW solutions

v(x , t) = f (y), y = x −λt, with the ODE

−λf



=−(| f | f



)



−|f |

−

(3.99)

3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 125

0 2 4 6 8 10

x 10

−4

−8

−6

−4

−2

x 10

−3

f(y)

oscillatory

non−oscillatory

(a) two types of interfaces

0 10 20 30 40 50

−3

−2

−1

φ(s)

(b) stable periodic orbit

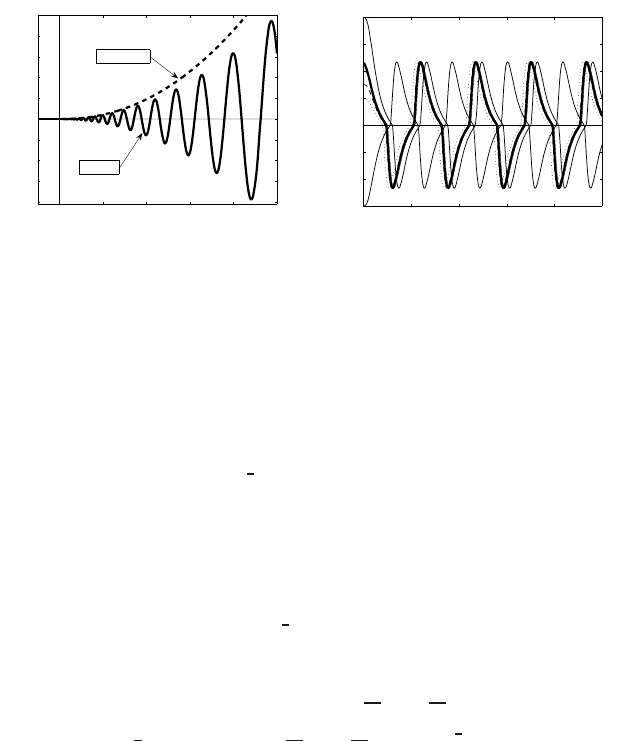
Figure 3.5 (a) Oscillatory and non-oscillatory behavior (3.101) close to the interface at y = 0,

and (b) convergence to the stable periodic orbit of the ODE (3.102).

Assume that f (y) has the interface at y = 0, with the trivial extension f (y) ≡ 0

for y < 0, and exhibits the “maximally regularity”, i.e., the best which is admitted

by this ODE. Then expressions like (3.97) with n = 1 are no longer true, i.e., the

strong absorption term is seriously involved in the oscillatory behavior. The leading

changing sign asymptotics are governedby the two-term ODE

(| f | f



)



+|f |

−

f = 0fory > 0, f (0) = 0, (3.100)

which is (3.99) with λ = 0. Hence, v = f (x) is just a stationary solution of (3.98).

The TW speed λ = 0 then enters the next expansion term, and this induces an inter-

esting dynamic interface equation, which the interested reader may derive as usual

(though the expansion is not easy). Instead of (3.97), with n = 1, we set

f (y) = y

ϕ(s), s = ln y, (3.101)

and, substituting into (3.100), derive the following ODE for ϕ(s):

H [ϕ] ≡



|ϕ|





+ 5ϕ









|ϕ|





+ 5ϕ







+|ϕ|

−

ϕ = 0.

(3.102)

We call ϕ(s) in (3.101) the oscillatory component of f (y). It turns out that (3.102)

admits a periodic solution of changing sign, and (3.101) then yields the oscillatory

behavior near the interface at y = 0; see Figure 3.5(a), the bold line. Figure 3.5(b)

shows convergence to this unique asymptotically stable periodic solution of (3.102)

for various initial data posed at s = 0. If the ODE (3.102) admits a positive equilib-

rium ϕ(s) ≡ ϕ

> 0 (actually, it does not), then (3.101) gives the non-oscillatory

behavior close to the interface at y = 0; see Figure 3.5(a), the dashed line.

According to (3.101), the periodic ϕ(s) gives the oscillatory behavior of solutions

of the maximal regularity at interfaces for the TFE with absorption (3.98). A rigor-

ous justiﬁcation that the formulae (3.101) and (3.102) correctly describe a generic

structure of multiple zeros of solutions v(x, t) of the PDE is a hard

OPEN PROBLEM.

Concerning similarity oscillatory extinction patterns satisfying the ODE (3.96)

(with modiﬁed coefﬁcients from (3.98)), numerical experiments show that such g =

126 Exact Solutions and Invariant Subspaces

0isnonexistent, i.e., the generic extinction behavior in the CP is not self-similar, as

in the FBP studied above.

Example 3.12 (Stabilization in the TFE) Consider the TFE (3.8) from lubrication

theory with an unstable, backward parabolic diffusion term,

=−(vv

xxx

)

− (

√

)

As shown in the previous example, we perform the change v = u

and obtain a PDE

with the same cubic operator F

in (3.74) plus a quadratic term,

=−

u(u

)

xxxx

− u

)

xxx

−

)

− (u

)

. (3.103)

Clearly, the quadratic operator admits subspace W

, and hence, by Proposition 3.11,

there exist solutions (3.76) on W

driven by the DS





=−12C

− 2C



=−60C

− 10C

Integrating the second ODE yields −

+6ln



=−10 t →−∞as t →∞.

Therefore, for any initial values C

(0)<0andC

(0)>0, corresponding to bell-

shaped compactly initial data u

(x ), the following holds: C

(t) →−

as t →+∞.

Once C

(t) is known, one can ﬁnd C

(t) from the ﬁrst equation, showing that C

(t)

stabilizes to a constant B > 0ast →∞. Plugging these expansions into (3.76), we

obtain the following asymptotic pattern:

u(x , t) =



B −



+ O



−



as t →+∞,

with the uniform convergence on bounded intervals in x. These exact solutions de-

scribe exponentiallyfast stabilization to a single proﬁle from the family of stationary

solutions of (3.103) that are parameterized by a constant B > 0. Then, λ

=−

the exponential term is the ﬁrst negative eigenvalue from the point (discrete) spec-

trum of the linear operator that appears in (3.103) after linearization about the sta-

tionary proﬁle (B −

)

3.4 Extinction behavior for sixth-order thin ﬁlm equations

Example 3.13 (Extinction, quenching, ... ) A Stefan–Florin FBP and the CP can

be posed for the sixth-order TFE with absorption

= (uu

xxxxx

)

− 1, (3.104)

where the invariant subspace is W

= L{1, x , x

, ..., x

} on which the PDE is a

seventh-order DS. Then, as shown in Section 3.2, we can describe the initial singu-

larity via Dirac’s mass, ﬁnite-time extinction, quenching and interface turning point

patterns, and can develop local existence-uniqueness approach to the FBP based on

the von Mises transformation (Example 3.10). For the sixth-order PDE (3.104), four

free-boundary conditions should be posed. The Cauchy problem exhibits special os-

cillatory patterns to be brieﬂy discussed.

3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 127

Example 3.14 (Zero contact angle conditions) To get four conditions (3.15), an-

other model is needed. Taking a sixth-order TFE with strong absorption,

= (vv

xxxxx

)

− v

we set v = u

and obtain a quartic operator F

in the PDE

= F

[u] −

, where F

[u] =



+ 3u



(3.105)

Similar to Proposition 3.11, F

admits W

= L{1, x, x

}, so there exists solution

v(x , t) = u

(x , t) =



(t) + C

(t)x



= 0), (3.106)

satisfying all four free-boundary conditions

v = v

= v

= vv

xxxxx

= 0 at the interface x = s(t).

The expansion coefﬁcients solve the DS





6!C

−



7!C

The second ODE yields C

(t) =−



7!t



1/3

< 0fort > 0, which results in, e.g.,

u(x , t) =



−



1 − t



−

(7!t)

1/3



. (3.107)

In rescaled variables, the extinction pattern as t → 1

−

has the asymptotic structure

u(x , t) = e

−τ



−

(7!)

1/3



+ O(e

−2τ

), y =

√

1−t

,τ=−ln(1 − t).

This agrees with the singular perturbed problem for the original rescaled solution v

given by (3.106), i.e., v(x, t) = e

−3τ

w(y,τ),wherew solves

=−

y + 3w − w

+ e

−τ

(ww

yyyyy

)

for τ  1.

The problem of passing to the limit τ →+∞in this PDE is

OPEN.

Concerning the dynamic interface equation, formulae (3.31), together with the

PDE (3.105), yield three interface operators on the right-hand side,



= S[u] ≡−60(u

)

xxx

− 90u

)

(3.108)

(the ﬁrst operator vanishes identically for u ∈ W

). Other free-boundary conditions

can be derivedfrom the DS by using the parameterizationvia (3.107), t =−

7!(u

)

In the local von Mises variable X = X (u, t), the free-boundary condition (3.108)

(and others) is necessary for the well-posedness of the corresponding problem for a

degenerate sixth-order symmetric linear differential operator. The analysis is simi-

lar to that shown in Example 3.10, but the mathematics and computations become

technically more involved.

On oscillatory solutions of the Cauchy problem. Consider the PDE extended to

{v<0} in the parabolic manner,

= (|v|v

xxxxx

)

−|v|

−

v in IR × IR

. (3.109)

128 Exact Solutions and Invariant Subspaces

TW analysis is the same, as in Example 3.10, and, instead of (3.99), the ODE is

−λf



= (|f | f

(5)

)



−|f |

−

f. Similarly, we neglect the left-hand side (or just set

λ = 0),

(| f |f

(5)

)



−|f |

−

f = 0fory > 0, f (0) = 0.

The oscillatory behavior exhibits a smoother envelope than in (3.101),

f (y) = y

ϕ(s), with s = ln y,

where the oscillatory component ϕ solves a sixth-order autonomous ODE which

describes the changing sign character of solutions of (3.109).Later on, we will show

a number of such ODEs that admit changing sign periodic solutions with oscillatory

behavior,as shown in Figure3.5(a). Such TW proﬁles satisfy at the interface at y = 0



(0) = f



(0) = f



(0) = f

(4)

(0) = 0,

and are smoother than O(y

) behavior given by (3.106) for the FBP.

Example 3.15 (Stabilization) Let us brieﬂyconsider stabilization in thelubrication

equation with an unstable diffusion perturbation,



xxxxx



−





As we have seen, setting v = u

yields the quartic operator F

in the PDE



+ 3u



−



+ 3(u

)



(3.110)

We obtain solutions (3.106) on W

= L{1, x

} with a slightly different DS





6!C

− 2C



7!C

− 14C

Taking initial values C

(0)<0andC

(0)>0 yields C

(t) →−

√

and the

following stabilization of solutions on W

u(x , t) =



B −

√



+ O



−14t/

√



as t →∞.

This shows that exact solutions on W

belong to the stable manifold of unstable

stationary solutions of (3.110), and that stabilization is exponentially fast.

3.5 Quadratic models: trigonometric and exponential subspaces

3.5.1 Blow-up and stability on W

for fourth-order TFEs

Consider thin ﬁlm operators with an extra zero-order quadratic term,

= F[u] ≡−uu

xxxx

+ βu

xxx

+ γ(u

)

+ δu

, (3.111)

where δ = 0, so that F cannot preserve a nontrivial polynomial subspace.

Proposition 3.16

Operator

(3.111)

preserves:

3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 129

(i) W

= L{1, cos x , sin x}

, provided that

δ = 1 −β − γ ; (3.112)

(ii) W

= L{1, cosh x, sinh x }

, provided that the same condition

(3.112)

holds;

(iii) W

= L{1, cos x , sin x, cos2x, sin2x },

provided that



10β + 8γ + 2δ = 17,

16β + 16γ + δ = 16.

(3.113)

In the case of (i), which will be analyzed later on in greater detail, we ﬁnd that the

TFE (3.111) possesses solutions

u(x , t) = C

(t) + C

(t) cos x + C

(t) sin x ,





= δC

− β



+ C





2,3

= (2δ −1)C

2,3

(3.114)

In the case of (iii) where (3.113) holds, there exist even solutions

u(x , t) = C

(t) + C

(t) cos x + C

(t) cos2x,









= δC

(δ + γ − β − 1)C

− 16βC



= (2δ −1)C

− 10βC



= (2δ −16)C

(δ + γ + β − 1)C

It is not difﬁcult to derive the DS on the full subspace W

in (iii). A typical example

of the operator preserving W

is (set δ = 1 in (3.113))

F[u] =−uu

xxxx

xxx

−

)

+ u

Example 3.17 (Regional blow-up: stability on W

) We next consider the TFE

with source

= F[u] ≡−(uu

xxx

)

+ 2u

. (3.115)

Let us see how the source term 2u

affects evolution properties of the solutions. As a

physical motivation of the model, let us mention that such a reaction term in the TFE

can be associated with a condensation of the ﬁlm substance from the surrounding

space (see the beginning of Section 3.2). The equation (3.115) is parabolic in the

positivity domain {u > 0}, so, in general, we have to deal with nonnegativesolutions

(by taking the positive part, as usual) of the corresponding FBPs, with the functional

setting as used in Sections 3.2 and 3.3. These well-posedness phenomena are not

essential for the current stability analysis on the invariant subspace W

Consider solutions on W

= L{1, cos x , sin x}, i.e.,

u(x , t) = C

(t) + C

(t) cos x + C

(t) sin x . (3.116)

The corresponding DS (3.114) is





= 2C

+ C



= 3C



= 3C

(3.117)

130 Exact Solutions and Invariant Subspaces

First of all, the DS (3.117) admits solutions for which C

= C

and C

= 0. Hence,

satisﬁes the single ODE



= 3C

⇒ C

(t) =

T −t

, (3.118)

where T > 0istheblow-up time of the explicit solution

(x , t) =

T −t

(1 + cosx) ≡

T −t

cos

(

). (3.119)

Taking the central wave of cos

(

) and setting u

= 0for|x |≥π yields a localized

blow-up solution satisfying, as t → T

−

(x , t) →∞ on the interval {|x| <π} and u

(±π, t) = 0.

The measure of this localization domain L

= 2π is called the fundamental length

of the regional blow-up. Note that (3.119) is a smooth solution satisfying conditions

(3.14) of zero contact angle and zero-ﬂux on the stationary interfaces at x =±π,

with n = 1. The local well-posedness of this FBP can be checked via the von Mises

transformation, as done in Example 3.10, but we cannot guarantee that such a local

unique construction can be extended up to the blow-up time, i.e., the solution will

remain strictly monotone near the interfaces. Recall that the existence of the simi-

larity solution (3.119) was interpreted as the result of invariance of the 1D subspace

= L{

cos

(

)} under the quadratic operator in (3.115). Another subspace is

−

= L{

sin

(

)}. In the CP, solutions are oscillatory; see Section 3.7.

Returning to the DS on W

, let us emphasizeanother importantaspect of evolution

on W

. We will show that all the blow-up orbits on W

asymptotically converge to

the above similarity solution u

on W

; that means its asymptotic stability on W

Proposition 3.18

Let blow-up happen in the DS

(3.117)

, i.e.,

(t) →+∞

t → T

−

< ∞

. Then there exists a constant translational parameter

such that,

uniformly in

x ∈ IR

(T − t)u(x, t) →

cos

(

x+a

)

t → T. (3.120)

Proof. Multiplying the second and the third ODE in (3.117) by C

and C

, respec-

tively, and subtracting, one obtains







= 0 ⇒ ∃ B ∈ IR such that C

= BC

By (3.116), this gives a in (3.120), but we need to study the DS



= 2C

+ (1 + B

, C



= 3C

. (3.121)

Setting C

= C

P in the equivalent ﬁrst-order ODE yields

+(1+B

⇒ C

P−(1+B

2+(1+B

This is easily explicitly integrated, but, for our purpose, it sufﬁces to note that



[2+(1+B

]dP

P−(1+B



= lnC

→∞

as t → T

−

. In this case, the denominator on the left-hand side tends to zero so

3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 131

→

1+B

and P →

√

1+B



or, which is similar, →−

√

1+B

; both equilibria

√

1+B

are stable



. Summing up, we have that, as t → T ,

u(x , t) ≈ C



1 +

√

1+B

cos x +

√

1+B

sin x



. (3.122)

Substituting C

= C

P ≈

√

1+B

into the ﬁrst equation in (3.121), we conclude

that C



≈ 3C

, and hence,

(t) =

T −t

(1 + o(1))

as in (3.118). Finally, (3.122) implies that (3.120) holds with tana =−B.

Thus, a symmetrization of the orbits of the DS occurs near the blow-up time, and

solutions (3.116) converge as t → T

−

to the separate variables pattern (3.119) up

to translation in space. In the general treatment of such a stability, introducing the

rescaled function

u(x , t) =

T −t

v(x ,τ), where τ =−ln(T − t) →+∞,

yields the fourth-order rescaled PDE

= F

∗

[v] ≡−(vv

xxx

)

+ 2v

− v. (3.123)

The asymptotic stability means that the rescaled solution tends to the similarity pro-

ﬁle, i.e., setting for simplicity a = 0,

v(x ,τ)→ g(x) =

cos

(

) as τ →∞,

where g(x ) is indeed a stationary solution of (3.123) satisfying

−(gg



)



+ 2g

− g = 0.

In rescaled variables, the stability of the blow-up solution reduces to the standard

stabilization to stationary solutions in equation (3.123). For the fourth-order TFEs,

this problem is

OPEN. For the related second-order parabolic PME

= (vv

)

+ 2v

− v, (3.124)

such stability of blow-up similarity solutions and stabilization results are well known

key. (3.124) is a gradient system in L

-metric (multiplication by (v

)

and integra-

tion over IR yields a Lyapunovfunction),while any potential and gradient properties

for (3.123) are unknown. Also, it is easy to show that the linearized operator



∗

[g] =−

(1 + cosx)

sin x

−

sin x



+ cos x



with the Dirichlet boundary conditions at x =±π is not symmetric in L

(−π, π)

for any weight ρ ≥ 0, and hence, does not admit a self-adjoin extension. The point

spectrum of F



∗

[g]isUNKNOWN. We expect that some useful estimates of the spec-

trum can be obtained, at least, by a hybrid analytic-numerical approach to guarantee

linearized stability of the similarity proﬁle g. As usual in blow-up stability problems,

sincethe 1980s;see [509, Ch.4], wheretheLyapunovand comparisontechniquesare

132 Exact Solutions and Invariant Subspaces

the positive eigenvalue λ = 1 with the eigenfunction g, which directly follows from

the PDE (3.123), must be excluded, since it corresponds to the shifting of the blow-

up time T that is ﬁxed by scaling. Eigenvalue λ = 0 is related to shifting in x ,and

this unstable mode can be forbidden by, say, symmetry about the origin.

On single point blow-up patterns on exponential W

. For the invariant subspace

= L{1, cosh x, sinh x }, the DS (3.117)remains the same, but the blow-upbehav-

ior is completely different. Namely, from the DS (3.121) with B = 0, we have

=−C

+ 3

+ ... as C

→+∞ (A > 0).

Estimating C

1,2

(t), this gives the blow-up behavior on W

as t → T

−

u(x , t) = (T − t)

−



A −

(T −t)

2/3

+ ...



= (T − t)

−

g(ξ) + ...

for small |x| > 0, where ξ = x /(T − t)

1/3

is the rescaled spatial variable and

g(ξ) = (A −

) is the limit rescaled proﬁle. Taking the positive part for proper

FBP setting, we observe two symmetric interfaces

(t) =±

√

6A(T − t)

+ ...

that collapse at the origin at t = T

−

. Such blow-up patterns with a lower blow-up

rate O((T − t)

−1/3

) are expected to be evolutionary unstable (an OPEN PROBLEM);

cf. the stable rate ∼ O((T − t)

−1

) in (3.120).

3.5.2 Sixth-order model with blow-up

It is easy to propose such a model, e.g.,

= (uu

xxxxx

)

+ 2u

with the same subspace W

= L{1, cos x , sin x} and the same DS (3.117). As in Ex-

ample 3.17, there exist localized blow-upsolutionson W

, and the similarity separate

variables solution is stable on W

. Note that W

= L{1, coshx, sinh x} is invariant

for the operator with absorption F[u] = (uu

xxxxx

)

− 2u

3.5.3 Partially invariant subspaces (modules) for quadratic operators

These results have a counterpart in the class of quadratic second-order operators;

see Example 1.43. Let us introduce the following one-parameter family of quadratic

fourth-order operators:

[u] =−uu

xxxx

+ β(u

)

+ (1 − β)u

xxx

(β ∈ IR ), (3.125)

which will be used later on in other applications.

Proposition 3.19

For any constant

γ = 0

, operator

(3.125)

admits

= L{1, coshγ x, sinh γ x }

and

−

= L{1, cosγ x, sin γ x}. (3.126)