Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics

Подождите немного. Документ загружается.

3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 103

In (3.17), we include three quadratic primitive monomial operators F

1,2,3

with simi-

lar actions on elementary polynomials, i.e., for any monomial x

(l ≥ 4),

] = c

M(l)

, where M(l) = 2l − 4

for j = 1, 2, or 3 with constants c

= 0. We then write F

] ∼ x

M(l)

. Obviously

(this is a general principle), for any M(l) ≤ l, the polynomial subspace W

l−1

L{1, x , ..., x

l−1

} is invariant under F

. Adding other quadratic terms with M(l) less

than 2l−4, suchas u

xxxx

, u

xxx

(M = 2l−5forboth),u

xxxx

, (u

xxx

)

(M =

2l −6), etc., will not affect the dimension of polynomial subspaces, although this can

change other aspects of mapping. The ﬁrst result is straightforward and establishes

the dimension of the basic invariant subspace that exists for arbitrary β and γ .

Proposition 3.1

Operator

(3.17)

preserves the 5D subspace

= L{1, x , x

, x

}. (3.18)

Proof. Indeed, it sufﬁces to check mappings of the higher-degree term, F[x

] ∼

2l−4

. For invariance, one needs 2l − 4 ≤ l, which yields l ≤ 4.

For solutions on W

u(x , t) = C

(t) + C

(t)x + C

(t)x

+ C

(t)x

+ C

(t)x

the TFE (3.17) is a ﬁfth-order DS













=−24C

+ 6βC

+ 4γ C



= 24(β − 1)C

+ 12(β + 2γ)C



= 24(2β + 2γ − 1)C

+ 18(β + 2γ)C



= 24(4β + 6γ − 1)C



= 24(4β + 6γ − 1)C

The last ODE is solved independently, and then the rest of the equations become

linear and give the explicit solutions.

The next question is about possible extensionsof the basic subspace (3.18). These

and further results can be extracted from Section 2.6.4. We present direct proofs in

view of their simplicity.

Proposition 3.2

Operator

(3.17)

preserves the following subspaces:

(i) W

= L{1, x, x

, x

15β + 20γ = 6;

(ii) W

= L{1, x , x

, x

4β + 5γ = 2;

(iii) W

= L{1, x , x

, x

β =

,γ=−

;

(iv) W

= L{1, x , x

, x

β =

,γ=−

(v) F

does not admit the 10D subspace

= L{1, x, x

, x

or polynomial subspaces of higher dimension.

Proof. (i) For arbitrary parameters β and γ , F : W

→ W

, and the given invariance

condition ensures vanishing the coefﬁcient of x

in the expansion of F[u]forany

u ∈ W

104 Exact Solutions and Invariant Subspaces

(ii) Similarly, F : W

→ W

, and the prescribed condition guarantees that the coef-

ﬁcients of x

and x

simultaneously vanish.

(iii) In this case, one needs to checkthe invarianceconditions implying vanishingthe

coefﬁcientsof x

, x

,andx

. Forfunctionsu = C

+...+C

∈ W

the following holds:

F[u] = ... +



180(4β + 5γ − 2)C

+ 30(49β + 56γ − 32)C



+60(35β +42γ − 20)C

+ 42(35β + 42γ − 20)C

In view of the independence of the terms C

and C

in the ﬁrst square bracket,

this leads to the following linear system for coefﬁcients β and γ :



4β + 5γ = 2,

49β + 56γ = 32,

35β + 42γ = 20.

The system has a unique solution indicated in (iii).

(iv) The result is straightforward for even polynomials u = C

+ C

∈ W

for which

F[u] = ... + 24(124β +140γ − 85)C

+ 112(24β + 28γ − 15)C

so that, for invariance, we need



124β + 140γ = 85,

24β + 28γ = 15.

This yields the operator in (iv). For arbitrary u ∈ W

, we use Reduce.

(v) The negative conclusion follows from Theorem 2.8 on the maximal dimension,

since the optimal estimate (2.19) yields

n ≤ (2k + 1)



k=4

= 9, (3.19)

where n is the dimension of the invariant subspace W

of the kth-order operator.

As an illustration of the proof of (v), it is not difﬁcult to check that plugging

u = C

+ C

x + ... + C

+ C

∈ W

leads to an inconsistent linear

system for the parameters {β,γ}.

Operators preserving subspaces of maximal dimension. According to Theorem

2.8, the maximal dimension of subspaces satisﬁes (3.19), i.e., it is nine for arbitrary

nonlinear fourth-order operators. Proposition 3.2(iv) shows a single such operator

from the family (3.17). Clearly, the maximal dimension is achieved for the quadratic

fourth-order fully nonlinear operator

[u] = (u

xxxx

)

, (3.20)

which has the minimal degree M(l) = 2l −8, and admits subspace W

in Proposition

3.2. Concerning general quadratic fourth-order operators (here u



= u

)

F[u] = α

(4)

)

+ α



(4)

+ α



(4)

+ α



(4)

+ α

(4)

+α



)

+ α





+ α





+ α



+α



)

+ α





+ α



+ α



)

+ α



+ α

(3.21)

3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 105

where α

+ ... + α

= 0, the following complete classiﬁcation result holds:

Proposition 3.3

There exist precisely three linearly independent operators from the

family

(3.21)

preserving subspace

in Proposition

3.2

.Theseare

(3.20)

and

[u] =−uu

(4)





−



)

[u] = u



(4)

−



)

The same operators follow from the general formulae in Theorem 2.36. F

given in Proposition 3.2(iv),andF

is the only new one. As in classiﬁcation of

second-order operators in Section 2.4, the ODE

(9)

= 0thatdeﬁnes W

is invariant under the 3D operator space spanned by {F

, F

Example 3.4 (Fourth-order p-Laplacian operator) The dimension of polyno-

mial subspaces may also increase for the higher-order p-Laplacian operators. For

instance, parabolic PDEs

=−∇·



|∇u|

∇u



(3.22)

appear in thin ﬁlm ﬂows in the capillary-driven case (the pressure is p = u), in

which the viscosity of the spreading liquid is temperature-dependent; see Remarks.

Setting n = 0andl = 1, consider the 1D operator

F[u] =−



xxx

)



Since here M(l) = 2l − 7, this admits W

from Proposition 3.2(iii).

3.1.3 Cubic operators

In the next example, consider the cubic operators from (3.7) with n = 2,

F[u] =−



xxx

+ βuu

+ γ(u

)



, (3.23)

where each monomial operator has M(l) = 3l − 4. Then the basic subspace for

any β and γ is W

= L{1, x, x

} (l = 3l − 4, i.e., l = 2), on which the principal

fourth-order operator in (3.23) annuls identically. This becomes nontrivial on some

extended subspaces.

Proposition 3.5

Operator

(3.23)

preserves the following subspaces:

(i) W

= L{1, x , x

, x

6β + 9γ =−2;

(ii) W

even

= L{1, x

, x

β =−

,γ=

(iii) W

= L{1, x , x

, x

}

is not invariant for any

and

γ ∈ IR .

(3.24)

Proof is straightforward. In (iii), we derive an inconsistent linear system for β, γ .

The monomial F[u] = (u

xxxx

)

satisﬁes, in our notation, F[x

] ∼ x

3l−12

and has

= L{1, x, ..., x

}. Most plausibly, this seven is the maximal dimension that is

achieved by cubic operators of this type.

106 Exact Solutions and Invariant Subspaces

3.2 Applications to extinction, blow-up, free-boundary problems, and

interface equations

We begin with a simple quadratic TFE using the basic polynomial subspace W

.It

reveals some interesting evolution properties of such models, which are not easy to

justify rigorously for more general classes of solutions.

3.2.1 Invariant subspace and exact solutions

We introduce a quadratic TFE with the constant negative absorption term,

=−(uu

xxx

)

− 1. (3.25)

It is common to have thin ﬁlm models in the divergent form, so the mass conserva-

tion holds. On the other hand, under some circumstances, TFEs may contain non-

divergentoperators. For instance, source-like terms may be relevant for a monolayer

ﬁlm in coexistence with vapor due to the well-studied phenomena of adsorption (in-

teraction of gases and liquids with solid surfaces) and condensation; see [83] and

[559] for more recent references. Homogeneous nucleation phenomena are natural

in phase transition theory (see Lifshitz–Pitaevskii [394]), and condensation of liquid

droplets from a supersaturated vapor is an example. Absorption terms can occur in

view of the evaporation phenomenon,or due to the permeability of the surface. Such

general non-divergent TFEs are derived in [451]; see also Remarks.

Evaporation and condensation phenomena have been a subject of research and

debate for more than a century. Classical nucleation theory dates back to Laplace’s

work (1806) on surface energy and tension, to Thompson’s (Lord Kelvin) theory es-

tablishing the Thompson formula (1870)for the dependence of the critical radiusr of

a droplet on the vapor pressure p, the famous condensation theory by Hertz (1882)

and Knudsen (1915), Becker–D¨oring’s equations of nucleation (1935), Zel’dovich–

Frenkel’s equation (1942), Lifschitz–Slyozov’s theory of coarsening (1961), and

other ideas and results. Papers [518, 394] contain detailed overviews of the history.

Equation (3.25) represents a formal mathematical model explaining key features

of extinction phenomena in Stefan–Florin FBPs for thin ﬁlm equations. For the

second-order PMEs, similar absorption models are

= (u

)

− u

, with σ>0andp > −(σ + 1), (3.26)

where p = 0 gives the constant absorption −1. These models exhibit interfaces,

ﬁnite-time extinction, and quenching in the strong absorption range p < 1, and are

key for general existence, uniqueness, interface propagation, and asymptotic theory;

see references and results in [245, Ch. 4, 5] and [226, Sect. 7.11].

For (3.25), a compactly supported nonnegative continuous initial function u

(x )

is taken. Then, formally, in the Cauchy problem, we want the constant absorption

term to act only in the positivity domain {u > 0}, since otherwise, the solution will

immediately take negative values. This implies that, instead of −1 everywhere, one

needs to have the absorption term −1χ

{u>0}

(x ),whereχ

(x ) is the characteristic

function of the set A ∈ IR ,soχ

(x ) = 1ifx ∈ A, and zero otherwise. Then the

3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 107

Heaviside function should be put into the right-hand side of (3.25) instead of −1,

H (u) =



1ifu > 0,

0ifu ≤ 0,

representing a strong discontinuous nonlinearity. We keep the use of the term −1in

the equation, since this cannot affect the construction of the explicit solutions. For

FBPs, the Heaviside function is not necessary. (By regular approximations, this can

be avoided in the CP as well; see below, though solutions are of changing sign.)

According to Proposition 3.1, restricting our attention to symmetric in x functions,

consider the solutions

u(x , t) = C

(t) + C

(t)x

+ C

(t)x

∈ W

= L{1, x

, x

}. (3.27)

Substituting into (3.25) yields a simple DS









=−24C

− 1,



=−72C



=−120C

(3.28)

The last ODE is integrated independently, C

(t) =

120t

,andtheﬁrst two equations

then become linear and give the explicit solutions

u(x , t) =



−

t − E

−

120t



, (3.29)

where A

> 0andE

≥ 0 are arbitrary constants, and (·)

denotes the positive

part. For these sufﬁciently smooth Lipschitz continuous in x solutions (3.29), the

zero-ﬂux condition is valid,

u = uu

xxx

= 0atx = s(t), (3.30)

but u

= 0 at the interface in general. The zero contact angle condition fails, and

hence, there occurs another FBP to be speciﬁed next. The zero contact angle version

of the FBP is considered later on in Example 3.10.

3.2.2 Free-boundary setting

It is easy to identify the dynamic free boundary equation governing propagation of

the interface. Since exact solutions u(x, t) are smooth functions (excluding t = 0

and the extinction time t = T to be studied separately), differentiating gives

u(s(t), t) = 0 ⇒ u



+ u

= 0 ⇒ s



=−

. (3.31)

From (3.25), using that, for sufﬁciently smooth C

-solutions, uu

xxxx

= 0onthe

interface, we infer that, at x = s(t), u

=−u

xxx

− 1, and this determines the

regularity dynamic interface equation



= S[u] ≡ u

xxx

at x = s(t) for t ∈ (0, T ). (3.32)

The interface operator S[u] on the right-hand side is of the third order and consists

of two interface operators. The second operator is non-positive, since u

≤ 0atthe

108 Exact Solutions and Invariant Subspaces

right-hand interface, while the ﬁrst one is positive, since

xxx

(s(t), t) =

s(t)>0, provided that s(t)>0.

This leads to a competition between terms of different signs in the interface equation

(3.32), and makes it possible to observe a complicated non-monotone behavior of

interfaces, which can have turning points to be studied below.

Apparently, equation (3.32) holds for any smooth solution u(x, t) satisfying two

free-boundary conditions (3.30), so it is just a manifestation of sufﬁcient regularity

of solutions. We are still short of a third condition to create a well-posed FBP, which

is assumed to admit a unique solution (given, of course, by (3.29)).

Let us now specify the actual governing dynamic interface equation generating

exact solutions (3.27). First of all, C

(t) =

120t

xxxx

, which yields the fol-

lowing time-parameterization on the invariant subspace:

t =

xxxx

Next, calculating the interface position s(t) from (3.27) in terms of the expansion

coefﬁcients yields

s(t) = R(C

(t), C

(t)) for t ∈ (0, T ), (3.33)

where R is an irrational function which is obtained from the bi-quadratic equation

+ C

= 0. Differentiating (3.33) and using the DS (3.28), we ﬁnally

arrive at the governing interface equation of the form



R(C

(t), C

(t)), where t =

xxxx

. (3.34)

The interface operator

R is now of the fourth order, so it differs from the already

known regularity equation (3.32). On the other hand, two equalities, (3.32) and

(3.34), imply a stationary Neumann-type condition on the interface,

xxx

R(C

(t), C

(t))



t=1/5u

xxxx

at x = s(t), (3.35)

which can replace the dynamic condition (3.34).

Thus we have posed the FBP, which can be locally analyzed by using the von

Mises transformation (x, t, u) → (u, t, X ), where, close to the interface,

X (u(x, t), t) ≡ x .

Then X satisﬁes a quasilinear fourth-order PDE degenerated at the interface, which,

in the new variables, is ﬁxed at the origin,

x = s(t) ⇐⇒ u = 0.

Therefore, two boundary conditions are given at u = 0:

(i) (3.32) that ﬁxes a class of sufﬁciently smooth solutions, and

(ii) (3.34) or (3.35) (both should be rewritten in terms of the new variables).

Such FBPs are difﬁcult from a mathematical point of view. It is worth recalling the

fundamental results in linear theory, where the well-posedness of boundary-value

problems are governed by the Lopatinskii–Shapiro conditions [401]. It is important

3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 109

to characterizenecessary general conditions for the arising nonlinearFBPs, to ensure

existence of a unique local-in-time solution for small u > 0 constructed by semi-

group methods of parabolic PDE theory. In general, these are

OPEN PROBLEMS.We

postpone an example of such an analysis for a simpler, but more physically relevant

FBP with the zero contact angle condition, as in (3.14).

More on second-order PME with absorption: interface equation. The mathemat-

ics of such FBPs for the TFE are difﬁcult, but, relative to some key features, are

similar to those for the second-order parabolic PDEs which are much better under-

stood. This counterpart of (3.25) is the PME with absorption (3.26) having p = 0

and σ = 1,

= (uu

)

− 1. (3.36)

Forthe Cauchyproblem,or,which is the same, for the maximal solutions constructed

by regular approximations (see [226, Ch. 7] for details), the derivation of the free-

boundary condition as the analogy of (3.32) is similar and leads to the dynamic

equation with the ﬁrst-order operator S,



= S[u] ≡−u

at x = s(t) for t ∈ (0, T ). (3.37)

It is known (see examples in [226, Sect. 7.11]) that (3.37) holds almost everywhere

(a.e.) for anyweak solutionof the Cauchyproblemfor (3.36) withboundednonnega-

tive compactly supported initial data. The proof relies on the Maximum Principle and

intersection comparison arguments based on Sturm’s Theorem on zero sets, [226,

Ch. 7], so we do not need the von Mises transformation creating a non-standard

parabolic problem with dynamic boundary conditions. There are other well-posed

FBPs for (3.36) with various higher-order dynamic free-boundary conditions that

differ from (3.37). Typical existence and regularity properties of such non-maximal

solutions are also driven by Sturmian intersection comparison arguments. Such gen-

eral FBP theory is developed in [226, Ch. 8]. All of these MP and the intersection

comparison techniques fail for higher-order TFEs.

3.2.3 Initial Dirac’s mass

We nowbeginto describe evolutionpropertiesof exactsolutionson W

that, actually,

do not critically depend on the particular FBP setting that was revealed above.

It follows that explicit solutions (3.29) create a singular short-time behavior as

t → 0

that reﬂects the initial singularity phenomenon, i.e., blow-up at t = 0

.We

choose special values A

= 1andE

√

for which (3.29) takes the form

u(x , t) =



−

t + t

−

(y)



, where f

(y) =



1 −

√

120



(3.38)

and y = x/t

1/5

. It is important that the proﬁle f

(y) itself satisﬁes the zero contact

angle condition at its interface point, i.e.,

) = f



) = 0aty

= (120)

110 Exact Solutions and Invariant Subspaces

u(x , t)

t ≈ 0

t ≈ 1

−

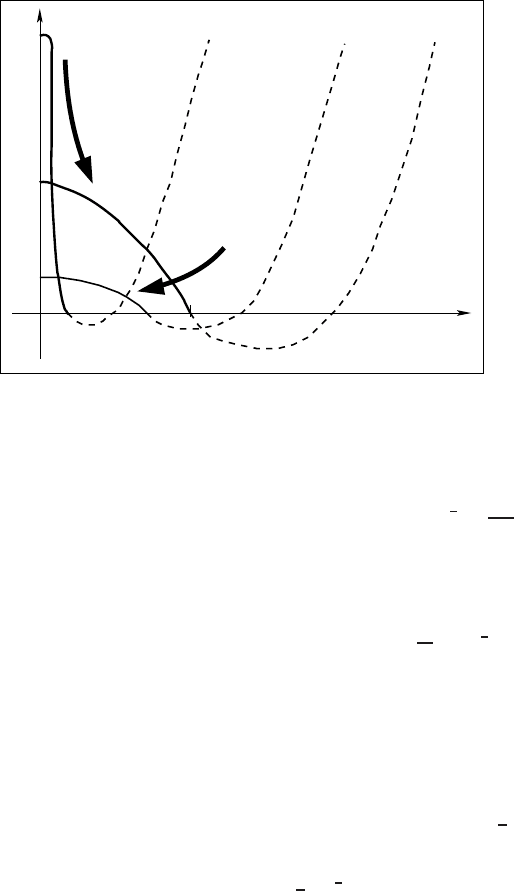
Figure 3.1 Evolution properties of solutions (3.38): (i) Dirac’s delta for t ≈ 0

, (ii) interface

turning point at t = t

, and (iii) extinction as t → 1

−

This is the rescaled similarity proﬁle of the pure quadratic TFE

=−(uu

xxx

)

, with the similarity solution u(x, t) = t

−



1/5



that has been recognized since the 1980s, [531]. Taking into account the spatial hump

concentrated near the origin inside the interval {|y|≤y

}, solution (3.38) satisﬁes a

remarkable initial condition given by a measure: as t → 0

u(x , t) → M

δ(x), with M

= 2



(y) dy =

(120)

where δ(x) is Dirac’s delta concentrated at x = 0. Figure 3.1 for t ≈ 0

illustrates

such a singular initial blow-up behavior.

3.2.4 Extinction patterns

Thus, explicit solutions (3.29) are generated by measures as initial data. As t > 0

increases, the phenomenon of ﬁnite-time extinction occurs. Setting A

now for

convenience,(3.29) gives at the origin x = 0 the following behavior:

sup

u(x , t) ≡ u(0, t) =



−

− t



Hence,u(x, t) vanishes at the extinctiontime T = 1, so that u(x , t) ≡ 0forallt ≥ 1.

The extinction and blow-up behavior are the main singularity formation phenomena

in nonlinear PDEs, especially in reaction-diffusion-absorptiontheory. There exists a

large amount of mathematical literature on these subjects, representing a practically

complete understanding of second-order parabolic PDEs; see key references in [245,

509]. For higher-order diffusion equations, the results are rare, and many types of

singularity patterns are not well-described and await rigorous treatment.

3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 111

Using (3.29) with A

, we will describe the ﬁnite-time extinction as t → 1

−

for the given FBP by using the corresponding rescaled independent variables

ξ =

√

1−t

and τ =−ln(1 − t) →+∞ as t → 1

−

. (3.39)

Then, rescaling solution (3.29) yields, up to exponentially smaller terms,

u(x , t) = e

−τ



1 − E

120

−τ



+ ... . (3.40)

For any constant E

> 0, we obtain a pattern which is expected to be asymptotically

stable in the rescaled sense, meaning simply that

u(x , t) →



1 − E



≡ g(ξ) as t → 1. (3.41)

Indeed, this illustrates stability of self-similar solutions of (3.25) of the form

(x , t) = (1 − t)g(ξ), ξ =

√

1−t

, where (3.42)

−(gg



)



−



ξ + g − 1 = 0, (3.43)

and g also satisﬁes the corresponding free-boundary conditions. Therefore, using

explicit solutions (3.29) implies that the self-similar behavior is stable, at least on

the subspace W

, where almost all solutions (excluding those with E

= 0tobe

analyzed below) asymptotically take the form of the self-similar ones.

The extension of stability analysis beyond the invariant subspace is a difﬁcult

OPEN PROBLEM, which has the following asymptotic setting: Given a general so-

lution u(x, t) of the FBP with extinction at t = 1andx = 0, the rescaled function

v(ξ,τ) = (1 −t)u(x, t), x = ξ

√

1 − t, satisﬁes the non-stationary rescaled PDE

=−(vv

ξξξ

)

−

ξ +v − 1, (3.44)

with the operator from (3.43).Thus, we arriveat theasymptotic stabilization problem

as τ →+∞. For the second-order PDEs, such as (3.36), the asymptotic extinction

behavior is well understood and proved rigorously (see [245, Ch. 5]), where the

analysis uses the MP, comparison, and intersection comparison approaches that do

not apply to higher-ordermodels.

3.2.5 On interface turning points

The interfaces of the explicit solution (3.38) are not monotone with time. The posi-

tion of the right-hand interface is

s(t) = (120)



1 −







so that s(0) = s(T ) = 0, where T =





,ands(t) attains its maximum at



125



At the moment t = t

∈ (0, T ), the solution has the turning point of the interface at

x = x

= s(t

). Therefore, close to the maximum point of s(t), the interface has a

speciﬁc quadratic behavior

s(t) − x

=−a

(t − t

)

+ ... , with some a

> 0. (3.45)

112 Exact Solutions and Invariant Subspaces

As we have seen, the turning point occurs due to the presence of two terms of differ-

ent signs in the regularity interface equation (3.32). This is a delicate phenomenon

in FBP theory. Even for the second-order PMEs with absorption, such as (3.36),

there are some mathematical open questions concerning the whole countable family

of different turning patterns. For instance, it is known that, for (3.36), the turning

kth pattern takes spatial shape related to the kth-order Hermite polynomial being

the eigenfunction of the corresponding linearized operator [241]. We are going to

develop a similar “spectral theory” for the TFE and detect corresponding kth-order

polynomials.

Solution (3.38) gives an extremely rare opportunity to explicitly study the turning

asymptoticpattern, which it is convenientto describe in coordinates that are rescaled

about the point (x

, t

) by setting

y = x

− x ≥ 0,ζ=

−t

≥ 0, and τ =−ln(t

− t). (3.46)

In view of the turning point characterization (3.45), using Taylor’s expansion, it is

not difﬁcult to obtain from (3.38) that, for small y > 0andτ  1,

u(x , t) =



y + e

−2τ



−c

+ c

ζ + c

−τ

+ c

−2τ

+ ...



, (3.47)

where c

denote some ﬁxed constants with c

0,1

> 0. Solving approximately the

equation u(x, t) = 0 yields the interface position y

(τ ) =

−2τ

+ ... , coinciding

with (3.45) if a

.Theﬁrst linear term in (3.47) is the asymptotic trace of the

stationary proﬁle G(y), about which the turning effect occurs via a certain focusing

phenomenon. Hence, G solves the stationary TFE

−(GG



)



− 1 = 0, G(y) = a

y + a

+ a

+ ... as y → 0

, (3.48)

where the expansion corresponds to the necessary free-boundary conditions at y =

0. Thus, a

=−

= c

), meaning that s



) = 0 by (3.32). The explicit

formula (3.47) is the asymptotic expansion about the stationary proﬁle G(y),sowe

set u(y, t) = G(y) + Y (y, t) to get the linearized PDE

=−(G(y)Y

yyy

)

− (YG



(y))

− (YY

yyy

)

, (3.49)

where the inhomogeneous term −(GG

yyy

)

− 1 has vanished due to (3.48) and the

coefﬁcients are G(y) = a

y + ... and G



(y) = 6a

+ ... as y → 0. Let us write

(3.49) in terms of the new spatial rescaled variable

Y (y, t) = e

−2τ

w(η,τ), where η =

√

−t

, (3.50)

that is associated with the already known behavior (3.47), to obtain the following

exponentially perturbed equation:

= Bw −e

−

− e

−3τ

(ww

ηηη

)

+ ... , (3.51)

where B is the linear degenerate fourth-order operator

Bw =−a

(ηw

ηηη

)

−

η + 2w. (3.52)

This operator is not symmetric and most plausibly does not admit a self-adjoint ex-

tension in any weighted L

-spaces. In general, the spectral properties of such non-