Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics
Подождите немного. Документ загружается.


3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 143
0 20 40 60 80 100 120
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
s
φ(s)
Figure 3.7 Formation of a heteroclinic connection ϕ
+
→ ϕ
−
for (3.166) as n → n
−
h
.
0 2 4 6 8 10
−0.01
−0.008
−0.006
−0.004
−0.002
0
0.002
0.004
0.006
0.008
0.01
s
φ(s)
(a) stabilization to ϕ
±
0 1 2 3 4 5
−4
−3
−2
−1
0
1
2
3
4
x 10
−5
s
φ(s)
(b) periodic behavior, enlarged
Figure 3.8 Solutions of (3.155) for m = 3andn = 1: stability of constant equilib-
ria ϕ
±
(a) and the unstable periodic behavior in between (b), ϕ(0) = 0.04, ϕ
(0) =
−0.0176896526588... .
first critical exponent n
1
=
7
6
until the corresponding heteroclinic bifurcation at
n
h
= 1.215053... (m = 4); (3.167)
see Figure 3.10. For n > n
h
, the behavior becomes more and more unstable. Smaller
values of n are discussed below.
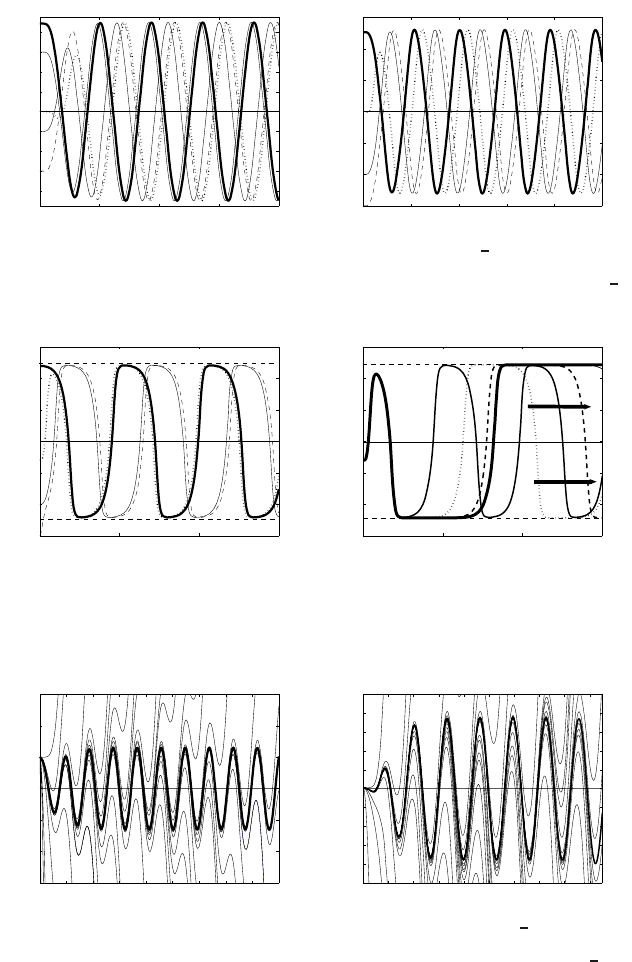
For m = 5, the unstable periodic behavior is shown in Figure 3.11. Cauchy data
for the periodic motion are: ϕ(0) = 10
−7
, ϕ
(0) = 4.838491256 × 10
−7
for n = 1
in Figure (a). In Figure (b), we have ϕ
(0) = 1.942533642 × 10
−6
for n =
9
8
.The
rest of the derivatives in both Figures (a) and (b) are equal to zero, ϕ
(0) = ϕ
(0) =
... = ϕ
(8)
(0) = 0.
According to these results checked numerically for several even and odd m,letus
state the following:
© 2007 by Taylor & Francis Group, LLC
144 Exact Solutions and Invariant Subspaces
0 5 10 15 20
−8
−6
−4
−2
0
2
4
6
8
x 10
−5
s
φ(s)
(a) n = 1
0 10 20 30 40 50
−6
−4
−2
0
2
4
6
x 10
−3
s
φ(s)
(b) n = n
1
=
7
6
= 1.1666...
Figure 3.9 Stable periodic behavior in the ODE (3.155), m = 4, for n = 1 (a) and n =
7
6
(b).
0 50 100 150
−0.03
−0.02
−0.01
0
0.01
0.02
0.03
s
φ(s)
(a) n = 1.215
0 50 100 150
−0.03
−0.02
−0.01
0
0.01
0.02
0.03
s
φ(s)
(b) n → n
−
h
= 1.2150534...
Figure 3.10 (a) Periodic structures of (3.155), m = 4, for n close to n
−
h
in (3.167); (b) de-
scribes formation of a heteroclinic connection (the wave moves to the right as n increases).
0 2 4 6 8 10 12 14 16 18
−3
−2
−1
0
1
2
3
x 10
−7
s
φ(s)
(a) n = 1
0 2 4 6 8 10 12 14 16 18
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
x 10
−5
s
φ(s)
(b) n = n
1
=
9
8
Figure 3.11 Unstable periodic behavior in (3.155), m = 5, for n = 1 (a) and n =
9
8
(b).
© 2007 by Taylor & Francis Group, LLC
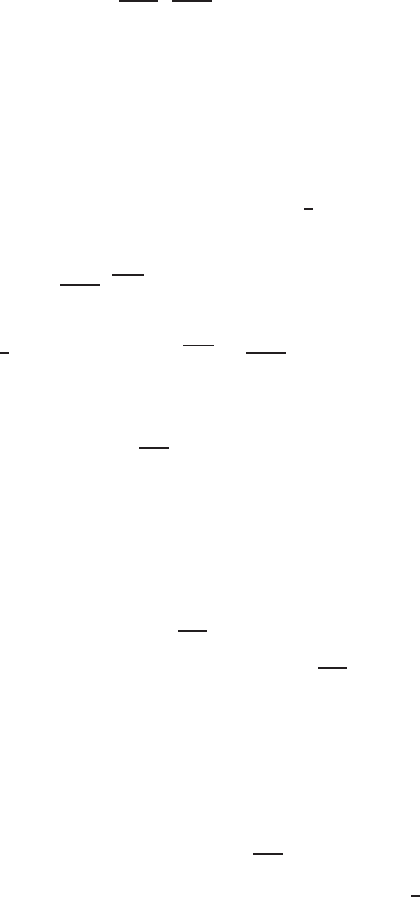
3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 145
Conjecture 3.1 (“On periodic solutions”) For any n ∈ (0, 1], the ODE (3.155)
admits a stable periodic solution for even m = 2, 4, ... and an unstable one for for
odd m = 3, 5, ... .
Thus, for even m, stable periodic solutions, existence of which for small n > 0
can be associated with continuity in n, persist for all n ∈ (0, 1]. Moreover, based on
numerical evidence, we also claim that they still exist for
n ∈ (1, n
h
), with some n
h
∈
2m−1
2m−2
,
2m−1
2m−3
= (n
1
, n
2
),
where n = n
h
is a heteroclinic bifurcation point for the corresponding (2m-1)th-
order ODE, as explained above. Such a non-oscillatory character of interfaces for
n > n
h
suggests that, somewhere in this parameter range, sign-preserving proper-
ties of special classes of solutions may exist leading to nonnegative solutions of the
Cauchy problem for sufficiently large n. This needs extra investigation and is an
OPEN PROBLEM.
Extrascalingasn → 0. The above figures show that the oscillatory behavior is not
directly detectable for small n > 0 and is numericallyinvisibleif n <
1
2
. To revealing
the limit oscillatory behavior as n → 0, where solutions of changing sign are of the
order
max|ϕ(s)|∼A(n) ≡
n
2m−1
2m−1
n
for small n > 0,
an extra rescaling in equation (3.155) is necessary,
ϕ(s) = Aψ(η), η =
s
a
, where a(n) = A
n
2m−1
=
n
2m−1
. (3.168)
Then, for small n > 0, function ψ(η) solves the ODE with Euler’s differential oper-
ator, which can be written in the form of
e
−η
(ψe
η
)
(2m−1)
− c
0
ψ
|ψ|
n
= 0 (3.169)
(as usual, all higher-order perturbations have been omitted). This is an easier ODE
than the original one (3.155), and contains the binomial coefficients. It turns out that
(3.169) possesses similar periodic orbits.
Numerical analysis gives solid evidence of the existence of stable periodic motion
for m = 2 in Figure 3.12, and for m = 4 in Figure 3.13, where the ODEs have the
form
m = 2: ψ
+ 3ψ
+ 3ψ
+ ψ +
ψ
|ψ|
n
= 0, and
ψ
(7)
+ 7ψ
(6)
+ 21ψ
(5)
+ 35ψ
(4)
+ 35ψ
+ 21ψ
+ 7ψ
+ ψ +
ψ
|ψ|
n
= 0
for m = 4(wetakec
0
=−1). Already for n = 0.1 in Figure 3.13(a), oscillations are
extremely small, since, by (3.168),
max|ϕ|∼10
−130
(n = 0.1, m = 4).
For n = 0.03 in (b), max|ϕ|∼10
−460
.
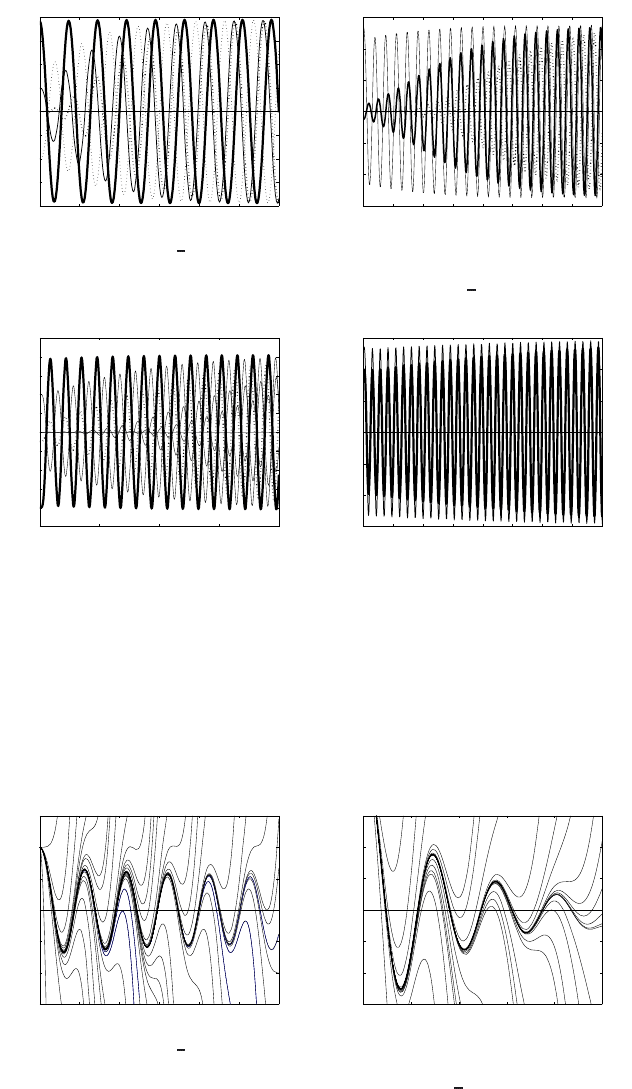
For m = 3, the corresponding rescaled ODE
m = 3: ψ
(5)
+ 5ψ
(4)
+ 10ψ
+ 10ψ
+ 5ψ
+ ψ −
ψ
|ψ|
n
= 0 (3.170)
admits an unstable periodic solution for small n > 0; see Figure 3.14(a) for n =
1
2
© 2007 by Taylor & Francis Group, LLC
146 Exact Solutions and Invariant Subspaces
0 5 10 15 20 25 30
−0.02
−0.015
−0.01
−0.005
0
0.005
0.01
0.015
0.02
η
ψ(η)
(a) n =
1
2
0 10 20 30 40 50 60 70 80
−3
−2
−1
0
1
2
3
x 10
−6
η
ψ(η)
(b) n = 0.16
Figure 3.12 Stable periodic behavior of (3.169), m = 2, for n =
1
2
(a) and n = 0.16 (b).
0 50 100 150 200
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
x 10
−3
η
ψ(η)
(a) n = 0.1
0 50 100 150 200 250 300 350 400
−2
−1
0
1
2
3
x 10
−11
η
ψ(η)
(b) n = 0.03
Figure 3.13 Oscillatory solutions of (3.169), m = 4, for n = 0.1 (a) and n = 0.03 (b).
(the Cauchy data to reveal the periodic motion are ϕ(0) = 2 × 10
−5
, ϕ
(0) =
−9.9850972244 × 10
−5
, other derivatives are equal to zero). Figure 3.14(b) shows
the case n = 0.2, where ϕ(0) = 5 × 10
−10
, ϕ
(0) =−1.4296767 × 10
−9
,andthe
periodic behavior is still not clearly seen. More details on such solutions and passage
to the limit n → 0
+
can be found in [175].
0 2 4 6 8 10 12
−3
−2
−1
0
1
2
3
x 10
−5
η
ψ(η)
(a) n =
1
2
0 2 4 6 8 10
−3
−2
−1
0
1
2
3
x 10
−10
η
ψ(η)
(b) n = 0.2
Figure 3.14 Unstable periodic behavior for (3.170) for n =
1
2
(a) and n = 0.2(b).
© 2007 by Taylor & Francis Group, LLC
3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 147
0 1 2 3 4 5 6 7 8
0
0.2
0.4
0.6
0.8
1
ξ
g(ξ)
FBP: g
1
CP: n=0
CP: n=1
FBP: g
2
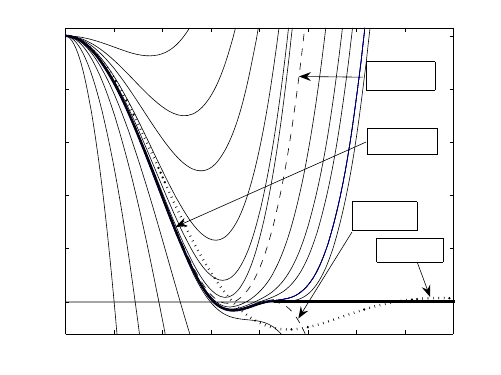
Figure 3.15 Similarity profiles g(ξ) satisfying (3.151), m = 2, for n = 1andn = 0. The
dashed lines denote the first FBP profiles, g
1
(ζ ) and g
2
(ζ ).
On existence of the fundamental similarity solution: dimension of linear bun-
dles. For m = 2, existence and uniqueness of the fundamental profile g satisfying
(3.151) are proved for n ∈ (0, 1),[174,Sect.9].Form ≥ 3, such results are un-
known. For using a shooting strategy from the interface point ξ = ξ
0
in (3.154)
(where, e.g., ξ
0
= 1isfixed by scaling invariance of the ODE) to the origin to match
m − 1 symmetry conditions, one needs to have an (m-1)-parametric stability bundle
about the periodic solution ϕ(s). According to (3.165) for n = 0, by continuity in
n, this bundle is expected to be precisely (m-1)-dimensionalfor small n > 0. Recall
that ξ
0
= 1, i.e., one parameter is fixed. This shows existence of g(ξ),inviewof
extremely good matching topology of the oscillatory bundle. Uniqueness is
OPEN.
For n ∈ (0, n
h
), we need to check the spectrum (the number of eigenvalues with
positive real parts) of the singular, non self-adjoint linearized operator with periodic
coefficients in equation (3.155),
P
2m−1
[ϕ] −(1 − n)c
0
|ϕ|
−n
I.
This is an
OPEN PROBLEM.
In Figure 3.15, we present similarity profiles of the CP given by the ODE (3.151),
m = 2, for n = 1 and, for comparison, the fundamental rescaled kernel for n = 0.
CorrespondingCauchy data are g(0) = 1andg
(0) =−0.3696375... for n = 1, and
g
(0) =−0.337989123... for n = 0. Here, g
1,2
(ζ ) are the first similarity profiles of
the zero contact angle, zero-flux FBP.
On negative exponents n. By continuity in n → 0, it can be expected that oscilla-
tory behavior of solutions of the Cauchy problem for TFEs persists for n < 0. The
representation (3.159) suits this case with the interface at y =+∞, where the oscil-
latory component ϕ solves the same ODE (3.155). Unlike in the case where n > 0,
for n < 0, the changing sign character of such solutions is difficult to detect, since
the ODEs involved exhibit extra blow-up singularities in finite y or s.Thisiseasily
© 2007 by Taylor & Francis Group, LLC

148 Exact Solutions and Invariant Subspaces
seen from (3.158), written in the form of
f
(2m−1)
= c
0
| f |
|n|
f
c
0
= λ(−1)
m
,
where the right-hand side is now superlinear for f 1, and, hence, there exists
monotone or oscillatory (always if c
0
< 0) blow-up in finite y. Moreover, typi-
cally an oscillatory behavior is not available, so that solutions of changing sign are
constructed by asymptotic expansion as n → 0
−
and extension in n;suchWKBJ
asymptotics are explained in [174, Sect. 7.6] for the TFEs with n → 0
+
.
3.8 Invariant subspaces in Kuramoto-Sivashinsky type models
The Kuramoto–Sivashinsky (KS) equation
u
t
=−u
xxxx
− u
xx
+ (u
x
)
2
(3.171)
is a semilinear fourth-order parabolic PDE with a quadratic Hamilton–Jacobi term
(u
x
)
2
. It was originally introduced as a model that describes flame front propaga-
tion in turbulent flows of gaseous combustible mixtures [526], and later it found
other applications in many areas of physics, including 2D turbulence; see Remarks.
The modified Kuramoto–Sivashinsky (mKS) equation contains an extra second-order
quadratic operator,
u
t
= F[u] ≡−u
xxxx
− u
xx
+ (1 − λ)(u
x
)
2
+ λ(u
xx
)
2
, (3.172)
where λ ∈ [0, 1] is a constant (λ = 0 leads to (3.171)), and describes dynamical
properties of hyper-cooled melt.
Example 3.33 (Instability) Let us begin with simple instability phenomena for the
mKS equation, which occur on the invariant subspace of periodic functions.
Proposition 3.34
For any
λ ∈ (0, 1)
, the quadratic operator in
(3.172)
admits sub-
space
W
3
= L{1, cosγ x, sinγ x}
,where
γ =
1−λ
λ
.
Consider solutions in the subspace of cos-functions,
u(x , t) = C
1
(t) + C
2
(t) cosγ x,
C
1
=
1
λ
(1 − λ)
2
C
2
2
,
C
2
=
1
λ
2
(1 − λ)(2λ − 1)C
2
.
It follows from the second ODE that λ>
1
2
leads to the exponentialinstability, while
for λ =
1
2
it follows that C
1
(t) = O(t) for t 1. On the other hand, for λ<
1
2
,
C
2
(t) is exponentially small as t →∞,andC
1
(t) is bounded, thus describing the
stability of the origin.
Let us introduce two models, exhibiting finite-time singularities.
Example 3.35 (Blow-up) Consider the KS equation with source
u
t
=−u
xxxx
+ (u
x
)
2
+ u
2
, (3.173)
© 2007 by Taylor & Francis Group, LLC

3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 149
where the reaction term u
2
is added, and the linear second-order term −u
xx
(not im-
portant for blow-up solutions) is ignored. Invariant subspaces of first-order quadratic
operators, such as (u
x
)
2
+ u
2
in (3.173), have been described in Section 1.4. Take
W
3
= L{1, cos x, sin x} on which the solutions u = C
1
+ C
2
cosx + C
3
sin x are
driven by the DS
C
1
= C
2
1
+ C
2
2
+ C
2
3
,
C
2
= 2C
1
C
2
− C
2
,
C
3
= 2C
1
C
3
− C
3
.
(3.174)
This quadratic system is similar to those studied for the TFEs in Example 3.17.
Though the last two ODEs contain extra linear terms, the proof of Proposition 3.18
remains unchanged. This gives a typical stability result on the subspace W
3
,where
all the blow-up solutions converge to the similarity pattern belonging to the 1D sub-
spaces W
±
1
. It is curious that the whole linear operator −u
xxxx
− u
xx
from (3.171)
vanishes identically on W
3
, the resulting DS does not contain any linear terms on
the right-hand side, simplifying stability analysis. The precise asymptotic behavior
as t → T for the DS (3.174) gives important properties of blow-up of 2π-periodic
solutions of (3.173); see references in the Remarks.
Example 3.36 (Extinction) In order to exhibit extinction phenomena, let us choose
the KS equation with absorption
u
t
=−u
xxxx
+ (u
xx
)
2
− 1. (3.175)
We restrict our attention to a lower-dimensional subspace W
3
= L{1, x
2
, x
4
} (which
is extended to W
5
by adding extra basic functions x and x
3
), and consider the evolu-
tion of the solutions u(x, t) = C
1
(t) + C
2
(t)x
2
+ C
3
(t)x
4
with the DS
C
1
= 4C
2
2
− 24C
3
− 1,
C
2
= 48C
2
C
3
,
C
3
= 144C
2
3
.
This system can be integrated and studied in a manner similar to that considered
in Section 3.2. The positive solutions satisfy the corresponding FBP which can be
studied by the von Mises transformation (see Example 3.10). The related singularity
formation phenomena for the uniformly parabolic PDE (3.175)are not as interesting
as those for the degenerate TFEs. On the other hand, the presence in the PDE of
the non-Lipschitz absorption term −1, which is actually |u|
p−1
u for p = 0(the
Heaviside function), makes the problem rather consistent, especially in the Cauchy
problem to be discussed next.
Finite propagation and oscillatory patterns in the Cauchy problem. Considering
(3.175) in IR × IR
+
, we face the question of the maximal regularity of solutions at
the interfaces. We present the signed version of this PDE for solutions of changing
sign,
u
t
=−u
xxxx
+ (u
xx
)
2
− signu.
As for TFEs with absorption, using the TWs u(x , t) = f (y), y = x − λt, yields
−λf
=−f
(4)
+ ( f
)
2
− sign f for y > 0, f (0) = 0.
© 2007 by Taylor & Francis Group, LLC

150 Exact Solutions and Invariant Subspaces
0 5 10 15 20
−0.015
−0.01
−0.005
0
0.005
0.01
0.015
s
φ(s)
Figure 3.16 The stable periodic behavior in (3.177).
Using our TFE experience, we keep two leading terms,
f
(4)
+ sign f = 0,
so the oscillatory component ϕ in the solution representation
f (y) = y
4
ϕ(s), where s = ln y, (3.176)
satisfies the autonomous fourth-order ODE
ϕ
(4)
+ 10ϕ
+ 35ϕ
+ 50ϕ
+ 24ϕ + sign ϕ = 0. (3.177)
Existence and uniqueness of periodic solutions are
OPEN.
Conjecture 3.2 The ODE (3.177) has a unique nontrivial periodic solution ϕ(s)
which is asymptotically stable as s →+∞.
Figure 3.16 showsthis stable periodicmotion obtainedfor differentinitial data. We
expect that, according to (3.176), such TW patterns describe the generic behavior of
solutions near interfaces in the CP.
Example 3.37 (Blow-up and interfaces in a quasilinear KS-type equation)Fi-
nally, let us present a simple quasilinear KS-type equation, which allows us to de-
scribe some crucial nonlinear phenomena by using simple mathematical tools. Con-
sider the following quasilinear fourth-order parabolic equation:
u
t
= F[u] ≡ u(−u
xxxx
+ u), (3.178)
which is initially formulated for nonnegative solutions. Clearly, the quadratic opera-
tor F preserves
W
5
= L{1, cos x , sin x, coshx , sinh x},
with simple blow-up dynamics. We restrict our attention to blow-up solutions in
separate variables
u(x , t) =
1
T −t
θ(x), (3.179)
© 2007 by Taylor & Francis Group, LLC

3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 151
where θ solves the linear ODE
−θ
(4)
+ θ = 1. (3.180)
Zero contact angle FBP. Let us posefor (3.178)the FBP with the zero contactangle,
u = u
x
= u
xx
= 0 at the interface at x = s(t), (3.181)
and bounded compactly supported initial data u
0
(x ) ≥ 0. The well-posednessof this
by exploiting a regularization in the degenerate term −uu
xxxx
, e.g., by replacing
u → ε +|u| (ε > 0),
in the PDE (3.178) and studying the convergence of the sequence {u
ε
(x , t)} of so-
lutions of such uniformly parabolic equations. (It is likely that more “singular” as
ε → 0
+
approximation is necessary to catch this FBP; such hard questions are not
discussed here and we refer to [44], where the dependence of solutions of TFEs on
approximations of the degenerate coefficient was studied first.) Further references
are given in the Remarks. The correspondence of the regularization to prescribed
free-boundary conditions is a difficult asymptotic problem that, in general, is
OPEN
for most degenerate parabolic PDEs, including the present one. The analytic regular-
ization
u →
√
ε
2
+ u
2
is expected to induce, as ε → 0, the solutions of the Cauchy problem; see below.
Thus, looking for even solutions of the ODE (3.180),
θ(x) = 1 + C
1
cos x + C
2
coshx ∈ W
5
,
and assuming that x
0
> 0 is the corresponding interface point, where (3.181) are
valid, we obtain the algebraic system
1 + C
1
cos x
0
+ C
2
coshx
0
= 0,
−C
1
sin x
0
+ C
2
sinh x
0
= 0,
−C
1
cosx
0
+ C
2
coshx
0
= 0.
(3.182)
The last two equations give a single transcendental equation for x
0
,
tan x
0
= tanh x
0
,
that possesses a countable set of roots {x
0k
} such that
x
0k
= π
k +
1
4
+ ... for k 1.
Solving the rest of equations in (3.182) yields the sequence of solutions
θ
k
(x ) = 1 −
1
2cosx
0k
cos x −
1
2coshx
0k
coshx for |x| < x
0k
.
These functions are strictly positive on (−x
0k
, x
0k
), which is easily seen for k 1,
and the oscillatory patterns satisfy
θ
k
(x ) → θ
±
∞
(x ) ≡ 1 +
(−1)
k
√
2
cosx > 0ask →∞ (3.183)
uniformly on compact subsets (θ
+
corresponds to even k and θ
−
to odd). There
© 2007 by Taylor & Francis Group, LLC
FBP can be checked locally by using the von Mises variables (see Example 3.10), or

152 Exact Solutions and Invariant Subspaces
exists a countable set {u
k
(x , t)} of standing wave blow-up solutions (3.179) of the
FBP localized in bounded intervals (−x
0k
, x
0k
).
On solutions of the Cauchy problem. Consider now the signed PDE
u
t
=|u|(−u
xxxx
+ u) in IR × IR
+
, (3.184)
with boundedcompactly supportedinitial data u
0
(x ) in IR . Thentheseparate-variable
solutions (3.179) yield the ODE
−θ
(4)
+ θ = signθ. (3.185)
Evidently, there exist strictly positive solutions θ
±
∞
(x ) given in (3.183), but we are
interested in compactly supported patterns.
It follows from (3.185) that, in the positivity and negativity domains respectively,
the profiles are
θ
±
(x ) =±1 +C
±
1
cosx + C
±
2
sin x +C
±
3
coshx + C
±
4
sinh x .
Despite such a simple form of profiles, the matching assumes four conditions of
continuity (here [·] denote the jumps of functions at zeros)
[θ] = [θ
] = [θ
] = [θ
] = 0,
so that the construction of changing sign solutions of the FBP leads to algebraic
problems for the eight expansion coefficients {C
±
k
} at each zero point x = x
0k
.This
is an
OPEN PROBLEM that can be tackled numerically.
The existence of changing sign solutions of the ODE (3.185) for both the FBP
and the CP problems is connected with general oscillatory properties of solutions of
the PDE (3.184). It is convenientto describe the oscillatory character of solutions by
TWs u(x, t) = f (x − λt),so
−λf
=−|f |f
(4)
in IR ,
whereweomit| f |f that is smaller near interfaces. Integrating once yields
f
= λ sign f ln| f | for y > 0, f (0) = 0.
We next introduce the oscillatory componentϕ,
f (y) = y
3
ϕ(ln y) ⇒ ϕ
+6ϕ
+11ϕ
+6ϕ = 3λs + λ signϕ ln |ϕ|. (3.186)
For λ<0, there exists the positive solution ϕ(s) =
1
2
λs + ... for s &−1. By
transformation in (3.186), this gives non-oscillatory behavior at the interface,
f (y) =
1
2
λy
3
ln y + ... > 0asy → 0, (3.187)
which corresponds well to the free-boundaryconditions (3.181). Oscillatory patterns
in the CP need extra study.
Oscillatory component. As usual, we introduce the family of PDEs
u
t
=−|u|
n
u
xxxx
, with parameter n ∈ (0, 1). (3.188)
Dividing by |u|
n
and setting v =|u|
−n
u yields a divergent quasilinear equation,
1
1−n
v
t
= [v] ≡−(|v|
σ
v)
xxxx
, with σ =
n
1−n
> 0. (3.189)
© 2007 by Taylor & Francis Group, LLC
