Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics

Подождите немного. Документ загружается.

5 Quasilinear Wave and Boussinesq Models. Systems 243

These heat-type models are intensivelystudied in Section 6.4. The similarity blow-up

solution of the S-regime takes the form

(x , t) =

√

T −t

f (x), (5.22)

where T > 0 is blow-up time and f (x) satisﬁes the same ODE

3( f



)



+ f

−

f = 0 (5.23)

(the constant

is replaced by 1 via scaling in f ). Such localized blow-up structures

for the gradient-dependent diffusion have been studied from the beginning of the

1980s; see details and references in [509, Ch. 4]. The compactly supported solution

of (5.23) is expressed in terms of the incomplete Euler Beta function B, and, in

particular, the measure of the support is [216]

= 2

π, (5.24)

which is called the fundamental length of this nonlinear medium with diffusion and

reaction mechanisms. A fundamental character of the length (5.24) is supported

mathematically: if x = s(t) is the right-hand interface of an arbitrary blow-up so-

lution u(x, t) ≥ 0 of (5.21) with compactly supported initial data u

(x ) having the

right-hand interface at s(0), then the localization holds, i.e.,

s(t) ≤ s(0) + L

for all t ∈ [0, T ).

The proof is based on the Sturmian intersectioncomparisonargumentwith the stand-

ing wave solution (5.22); details are given in [509, p. 245].

For the corresponding wave equation (5.19), any estimates of the blow-up inter-

face propagationare

OPEN PROBLEMS. There is also another fundamentaldifference

between the above parabolic (5.21) and hyperbolic (5.19) PDEs with the same cubic

operator. While the Cauchy problem for the parabolic equation is well-posed and

there exists a unique weak local-in-time solution for any integrable compactly sup-

ported data u

(see [148, 309]), the hyperbolic PDE (5.19), admitting, possibly, an

inﬁnite number of shock wave discontinuities, needs a delicate adaptation to such

nonlinearities of extensions of nonlinear semigroups (e.g., along the lines of Bres-

san’s approach to 1D systems of conservation laws [81]).

The anharmonic lattices are obtained by a discretization of the PDE and admit a

Hamiltonian representation. In Section 9.5, we study some lattices with breather so-

lutions, which are “almost” compact (solutions cannot be compactly supported on a

lattice, but the rate of spatial decay is super-exponential, which is typical for implicit

difference schemes for degenerate quasilinear operators of the PME or p-Laplacian

type). In the continuumlimit, such discrete breathers correspond to compact ones for

the PDE (5.19), which are periodic solutions in separable variables.

Example 5.6 (Blow-up patterns and compact breathers for quadratic opera-

tors) Consider the following quadratic p-Laplacian operator in IR

[u] =∇·(|∇u|∇u) + u

, (5.25)

244 Exact Solutions and Invariant Subspaces

which is also variational with the potential

(u) =−



|∇u|

dx +



dx for u ∈ W

1,3

(IR

) ∩ L

(IR

Invariant subspaces for operators in IR

are systematically studied in Chapter 6.

Here, we borrow a simple result from Section 6.1.3 (Proposition 6.9): the operator

(5.25) is associated with the 2D subspace

= L{1, f (x)}, (5.26)

where f is a solution of the following elliptic equation:

[ f ] − f ≡∇·(|∇ f |∇ f ) + f

− f = 0inIR

. (5.27)

Namely, for any C

∈ IR and C

≥ 0,

+ C

f ] = C

+ 2C

f +C

[ f ]

≡ C

+ (C

+ 2C

) f ∈ W

(5.28)

In particular, this means that F

admits an invariant cone, K

={C

1,2

≥ 0}.

Compactly supported continuous weak (i.e., understood in the sense of distribu-

tions) solutions of (5.27) have been recognized since the beginning of the 1980s

[216]; see details in Example 6.52. The equation (5.27) admits a nonnegative radi-

ally symmetric compactly supported solution f (x) in any dimension N ≥ 1, [229].

Using this invariant subspace, consider ﬁrst the blow-up behavior in the corre-

sponding parabolic equation

= F

[u]inIR

× IR

. (5.29)

Then, substituting

(x , t) = C

(t) + C

(t) f (x) (5.30)

into the PDE, in view of (5.28), yields the DS





= C



= C

+ 2C

where C

(t) is assumed to be nonnegative. The ﬁrst ODE gives C

(t) =−

, and,

integrating the second equation with C

> 0 yields the explicit blow-up pattern

u(x , t) =−

(T −t)t

f (x), (5.31)

where T > 0 is the blow-up time. Turning a blind eye to the behavior of this solution

at the initial moment of time t = 0 (see Example 6.52 for explanations), we observe

the regional blow-up as t → T

−

, where the solution (5.31) blows up only inside the

support of f (x), i.e., for any x in the positivity domain {f > 0}.

Consider next the corresponding hyperbolic PDE with an extra linear term on the

right-hand side necessary to create a breather solution,

= F

[u] − u in IR

× IR . (5.32)

Using solutions (5.30) yields a more difﬁcult 4D DS (with C

≥ 0)





= C

− C



= C

+ (2C

− 1)C

(5.33)

5 Quasilinear Wave and Boussinesq Models. Systems 245

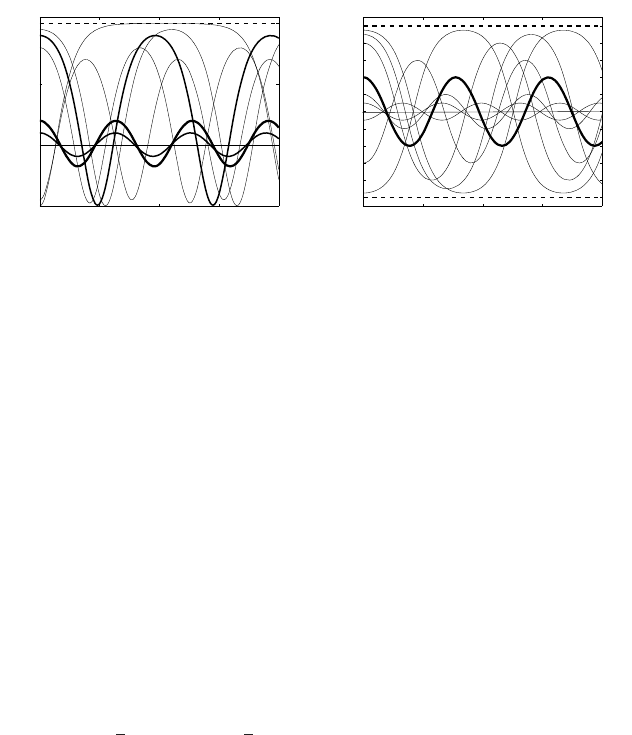
0 5 10 15 20

−0.5

0.5

(t)

(a) (5.33): C



= C

− C

0 5 10 15 20

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

(t)

(b) (5.34): C



=|C

− C

Figure 5.2 Periodic patterns in breather ODEs (5.33) and (5.34).

The standard breather solution is obtained for C

(t) ≡ 0, where a slightly different

PDE appears,

=∇·(|∇u|∇u) +|u|u − u.

Here C

may change sign and satisﬁes a single ODE



=|C

− C

(5.34)

that possesses periodic solutions via Jacobi’s elliptic functions; see Figure 5.2.

In the full DS (5.33), we initially ﬁnd a solution

(t), and next consider the

second ODE with a given linear force (2

(t) −1)C

. Recall the hypothesis C

≥ 0

which may essentially affect dynamics on this invariant subspace.

Example 5.7 (Breathers and blow-up in higher-order p-Laplacian PDEs) Con-

sider the fourth-order p-Laplacian operator with source

[u] =−(|u|u) + u



or with u

→ |u|u



which has the potential

(u) =−



|u|

dx +



dx for u ∈ W

2,3

(IR

) ∩ L

(IR

The above analysis is similar, where f solves a more complicated (variational) ellip-

tic equation

[ f ] − f ≡−(|f |f ) + f

− f = 0inIR

(or f

→ | f | f ). (5.35)

In particular, such compactly supported f (x ) generate compact breather solutions

(x , t) = C

(t) f (x ) of the corresponding hyperbolic PDE (5.32), as well as local-

ized blow-up patters u

(x , t) = (T −t)

−1

f (x) of the parabolic equation (5.29). The

same DSs occur on the invariant cone in subspace (5.26).

Restricted to radial solutions, (5.35) is a difﬁcult fourth-order nonlinear ODE that

admit oscillatory solutions near ﬁnite interfaces for the CP; see Example 5.9. For

this ODE, existence is checked numerically. The proﬁle (a) in Figure 5.3 is the ﬁrst

solution f

(x ) of the ODE (5.35) in 1D. To underline a universality character of

formation of compact and localized structures,for comparison,we include curves (b)

246 Exact Solutions and Invariant Subspaces

0 1 2 3 4 5 6 7 8 9

0.2

0.4

0.6

0.8

1.2

f(x)

(b), f

(a), f

Figure 5.3 Compactly supported solutions of (5.35), N = 1 (a) and (5.36) (b).

that are ﬁrst two compactly supportedproﬁles f

(x ) and f

(x ) of the non-variational

ODE

−(| f



)



+ f

− f = 0inIR . (5.36)

This appears in constructing blow-up patterns for the reaction-diffusion PDE with a

non-potential p-Laplacian,

=−(|u

xxx

)

+ u



or breathers for u

=−(|u

xxx

)

+ u

− u



In both ODEs, replacing f

→ | f | f does not make any essential change in the

solutions, in view of smallness of their oscillatory tail. Proof of existence, unique-

ness of a bell-shaped solution, and overall multiplicity (typically countable sets for

variational equations, as in the next example) are

OPEN PROBLEMS.

Example 5.8 (Higher-order porous medium-type operators)Considernowequa-

tions containing PME-type operators with the parameter n > 0,

+ u =−

(|u|

u) +|u|

u (hyperbolic: breathers),

=−

(|u|

u) +|u|

u (parabolic: blow-up).

The solutions in separate variables have the same form,

u(x , t) = C

(t) f (x), C



− C

, or C

(t) = (T − t)

−

, (5.37)

where a compactly supported f solves the following elliptic (variational) equation:

−

(| f |

f ) +|f |

f −

f = 0inIR

. (5.38)

For N = 1, such ODEs occurred earlier in compacton theory; see Example 4.7,

where some proﬁles {f

(x )} were constructed numerically (such countable sets are

associated with the variational setting).

Thus, formulae (5.37) and (5.38)give countablespectra of both compact breathers

and localized blow-up patterns.

Example 5.9 (p-Laplacian: oscillatory solutions in parabolic models)AsinEx-

ample 3.37, we take the 1D parabolic equation with the parameter n > 0,

= F[u] ≡−





in IR × IR

, (5.39)

5 Quasilinear Wave and Boussinesq Models. Systems 247

where F is a monotone monotone in L

(IR ), i.e., integrating by parts yields



(F[u] − F[v])(u − v)dx =−



−|v

)(u

− v



dx ≤ 0

for all smooth compactly supported function u,v ∈ C

∞

(IR ). For parabolic PDEs

with monotone operators, there exists powerfulexistence-uniquenesstheory of weak

solutions; see [396, Ch. 2]. In order to understand the oscillatory nature of such

of distributions, and consider sufﬁciently regular weak solutions that have a limit as

n → 0

, meaning a connection with the linear bi-harmonic PDE

=−u

xxxx

in IR × IR

This has the oscillatory fundamental solution with the asymptotics (3.195).

Let us describe oscillatory properties of solutions of the quasilinear equation(5.39)

by studying its fundamental solution

b(x, t) = t

−β

F(ζ ), ζ =

, where β =

3n+4

and F satisﬁes the ODE that is obtained after integration,









= βζ F in IR . (5.40)

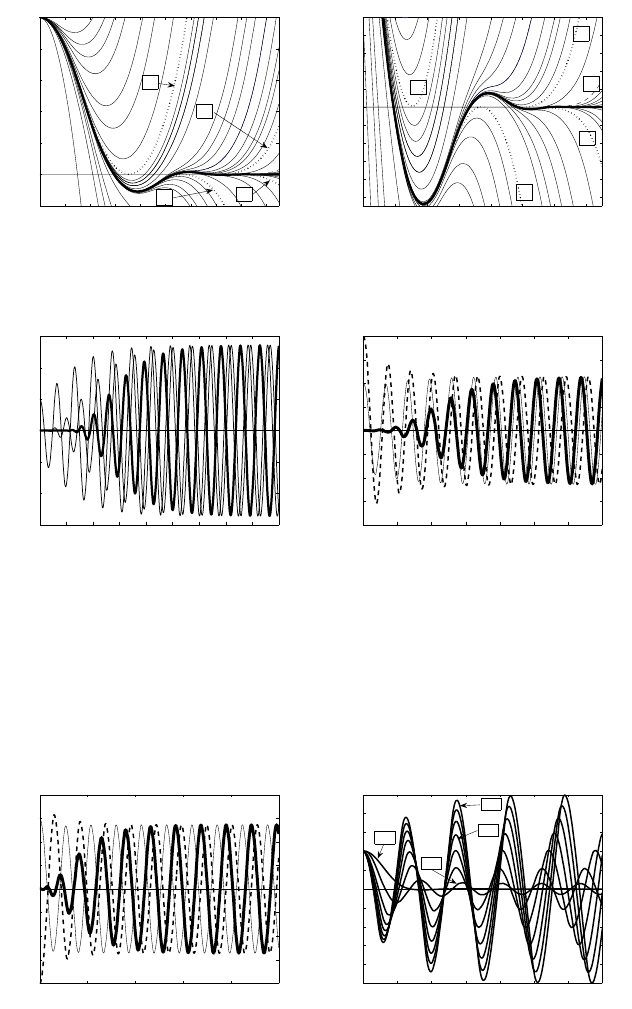
In Figure 5.4(a), we present a compactly supportedsimilarity proﬁle F(ζ ) for n = 1,

normalized so that F(0) = 1andF



(0) = 0 by symmetry. It is constructed by

shooting from ζ = 0 and corresponds to F



(0) =−0.3938136507879.... In (b), the

oscillatory character of F near the interface at ζ = ζ

is shown and will be studied

in detail next. We also specify in (b) a few zero contact angle FBP proﬁles F

, ...,

, corresponding to smooth touching the ζ-axis (a correct setting of this FBP is not

straightforward). In general, in view of changing sign behavior of F(ζ ) as ζ → ζ

−

there exists a sequence of FBP proﬁles {F

(ζ )} such that the solution of the CP

satisﬁes

F(ζ ) = lim

k→∞

(ζ )

uniformly. The proof is straightforward for n = 0, i.e., for the linear equation (5.40),

and is

OPEN and difﬁcult for n > 0. Notice that, by construction, each F

(ζ ) has

precisely k − 1 zeros inside the support for ζ>0, which is a kind of Sturm’s

property for higher-order ODEs that is not associated with the Maximum Principle.

Assuming that F is compactly supported on some interval [−ζ

,ζ

], let us intro-

duce the oscillatory component by setting

F(ζ ) = (ζ

− ζ)

ϕ(s), s = ln(ζ

− ζ), where γ =

3+2n

, (5.41)

so that we are looking for oscillatory behavior, as in Figure 3.5(a). Omitting expo-

nentially small perturbations, we obtain the ODE for ϕ(s),

(n + 1)





+ (2γ − 1)ϕ



+ γ(γ − 1)ϕ







+ 3(γ − 1)ϕ



+(3γ

− 6γ + 2)ϕ



+ γ(γ − 1)(γ − 2)ϕ



=−βζ

ϕ.

(5.42)

The oscillatory character of solutions is shown in Figure 5.5 for ζ

= (3n +4)(n+1).

The stable periodic solution gets smaller if n continues to decrease. For n = 0.8, the

periodic orbit is already of the order 10

−6

, while for n = 0.5, the oscillations are of

solutions, as in Example 3.37 (see equation (3.189)), we write (5.39) in the sense

248 Exact Solutions and Invariant Subspaces

0 1 2 3 4 5 6 7 8 9

−0.2

0.2

0.4

0.6

0.8

F(ζ)

(a) F(ζ ), the bold line

2 3 4 5 6 7 8 9

−0.1

−0.08

−0.06

−0.04

−0.02

0.02

0.04

0.06

0.08

0.1

F(ζ)

(b) F(ζ ), oscillations enlarged

Figure 5.4 The CP similarity proﬁle satisfying (5.40), n = 1; F

denote FBP proﬁles.

0 1 2 3 4 5 6 7 8 9

−3

−2

−1

x 10

−5

φ(s)

(a) n = 1

0 1 2 3 4 5 6 7

−4

−3

−2

−1

x 10

−6

φ(s)

(b) n = 0.8

Figure 5.5 Periodic behavior for (5.42) with n = 1 (a) and n = 0.8(b).

the order 10

−9

.Forlargern ≥ 2, the stable oscillatory periodic patterns are shown

in Figure 5.6.

On the other hand, using TWs u(x, t) = f (y), with y = x −λt in the PDE (5.39)

0 2 4 6 8 10

−4

−3

−2

−1

x 10

−3

φ(s)

(a) n = 2

0 1 2 3 4 5 6 7

−0.05

−0.04

−0.03

−0.02

−0.01

0.01

0.02

0.03

0.04

0.05

φ(s)

n=8

n=5

n=2

n=1

(b) 2 ≤ n ≤ 8

Figure 5.6 Stable periodic behavior for (5.42) with n = 2 (a) and n = 2, 3, 4, 5, 6, 7, 8(b)

(the amplitude is monotone increasing with n).

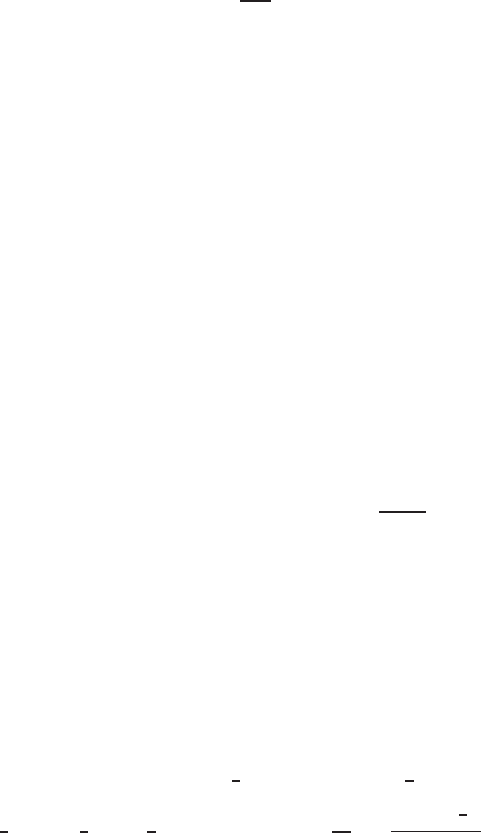
5 Quasilinear Wave and Boussinesq Models. Systems 249

yields the ODE

λf





| f







for y > 0, f (0) = 0,

where the interface is now at y = 0

. Setting as in (5.41)

f (y) = y

ϕ(s), where s = ln y,

yields precisely the ODE (5.42), with λ =−βζ

. Therefore, Figures 5.5 and 5.6 also

show the oscillatory character of TW solutions for any λ<0. For λ>0, (5.42)

admits a positive constant solution, e.g., for n = 1, it is

ϕ(s) ≡

2400

. (5.43)

The constant solutions for λ>0, such as (5.43), are stable. As shown in Example

4.54, on the basis of the linear PDE for n = 0, we claimed that a periodic solution

ϕ(s) for λ>0 does not exist.

Example 5.10 (On degenerate hyperbolic models: ﬁnite propagation and oscil-

latory behavior) Here, we review some hyperbolic PDEs with possible oscillatory

behavior near ﬁnite interfaces.

Fourth and sixth-order PDEs. The TWs for the fourth-order wave equation

=−





, with n > 0, (5.44)

are governed by the second-order Hamiltonian ODE λ

f =−|f



that does

not admit solutions decaying to zero. This indicates that the propagation via smooth

TWsisinﬁnite and solutions are oscillatory at inﬁnity (as for n = 0).

Consider next a similar sixth-order hyperbolic PDE,





xxxx

, with parameter n > 0, (5.45)

for which sufﬁciently smooth TW proﬁles solve the fourth-order ODE

f =









for y > 0, f (0) = 0. (5.46)

Solutions of the maximal regularity with a ﬁnite interface at y = 0aregivenby

f (y) = y

ϕ(s), s = ln y, where γ =

2(n+2)

, (5.47)

with e.g., ϕ(s) ≡ ϕ

(for n = 1, we have f ∈ C

and f

(5)

is Lipschitz continuous at

y = 0).The oscillatory componentϕ solves the same fourth-orderODE, as appeared

in Example 4.10 (with ϕ → ϕ



), where no periodic changing sign solutions were

showntoexist.

Linear PDEs: fundamental solutions and TWs. To conﬁrm the non-oscillatory

character of solutions of (5.44) and (5.45), it is useful to apply the continuous con-

nection as n → 0 with the corresponding linear hyperbolic equations (cf. Example

=−u

xxxx

in IR × IR

, (5.48)

with the fundamental solution b(x , t) =

√

tg(y), with y = x /

√

t,where

(4)





y −

g = 0 ⇒ g(y) =

2π



∞

sinz cos(

√

zy)

3/2

dz.

3.37 and equation (3.188)). Concerning (5.44), we take

250 Exact Solutions and Invariant Subspaces

It follows that g(y) is not compactly supported (the oscillatory part is given by

g(y) ∼ cos(

) as y →∞), so there is not ﬁnite propagation for (5.48) and

with n = 0 describing ﬂexural oscillations of an elastic beam,

= u

xxxxxx

, (5.49)

the oscillatory and inﬁnite propagation properties are seen from its fundamental so-

lution

b(x, t) = t

g(y), y = x/t

, where g(y) =

3π



∞

sinz cos(z

1/3

5/3

dz.

Let us next study TWs, solving

(4)

− λ

f = 0, with the characteristic equation µ

= λ

> 0,

so the decaying solutions are not oscillatory near the left-hand inﬁnite interface at

y =−∞, which become the linear counterparts of those in (5.47) with the con-

stant ϕ

. In addition, there exist non-decaying oscillatory solutions like f (y) =

cos(

√

|λ|y) (similar ones are admitted by (5.46)). The TW analysis also conﬁrms

that linear hyperbolic PDEs, such as (5.48), (5.49), and others do not allow ﬁnite

propagation, unlike the canonical second-order model u

= u

Remark 5.11 Finite propagation with λ =±1 exists in higher-order hyperbolic

PDEs, such as

tttt

= u

xxxx

, etc.

(strong estimates are obtained by multiplication by u

in L

). Odd-order linear dis-

persion equations u

ttt

= u

xxx

, etc. admit TW propagation with λ =−1 only.

More higher-order models. Consider TWs for a similar sixth-order PDE



xxx



xxx

, where



| f







− λ

f = 0fory > 0, f (0) = 0.

This ODE admits the strictly positive solution

f (y) = ϕ

, with a ϕ

> 0andγ =

3n+4

so there exists a class of non-oscillatory TW and other solutions. The ODE for the

component ϕ(s), with s = ln y,is

f (y) = y

ϕ(s) ⇒ P

[ϕ] =

n+1

[ϕ]|

, (5.50)

where the operators P

and P

are given in (4.93) and (3.166) respectively. Figure

5.7 shows a decaying unstable behavior for (5.50), n = 1, which is not periodic, so

cannot be extended to the interface at s =−∞(y = 0).

Thus, oscillatory interfaces occur for, at least, eighth-order hyperbolic models,

=−



xxxx



xxxx



or u

=−





xxxxxx



Recall the fruitful change v = u

xxxx

. Then the linear PDE for n = 0hastheTW

equation of sixth order,

=−u

xxxxxxxx

⇒ f

(6)

+ λ

f = 0,

solutions are oscillatory (cf. similar conclusions for (5.44)). Analogously, for (5.45)

5 Quasilinear Wave and Boussinesq Models. Systems 251

0 0.1 0.2 0.3 0.4 0.5 0.6

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

x 10

−6

φ(s)

Figure 5.7 Unstable decaying behavior for ODE (5.50) for n = 1. Cauchy data are ϕ(0) =

−6

, ϕ



(0) = ϕ



(0) = 0, ϕ



(0) = 0.000252638746... .

with the characteristic polynomial µ

+ λ

= 0, conﬁrming that the interface at

y =−∞is oscillatory, and remains oscillatory for small n > 0 by continuity; on

passing to the limit n → 0, see [174, Sect. 7.6].

Example 5.12 (Finite propagation in singular dispersive Boussinesq equations)

Let us next brieﬂydiscussﬁnite propagation in semilinear hyperbolic models. First,

consider the semilinear wave equation with a strong absorption (force) term,

= (−1)

m+1

u −|u|

p−1

u, with p < 1.

Studying TWs near ﬁnite interfaces leads to the ODE

(−1)

m+1

(2m)

−|f |

p−1

f = 0 ⇒ f (y) = y

ϕ(ln y), γ =

1−p

. (5.51)

Stable and unstable periodic behavior of ϕ(s) appears in TFE theory; see Section

3.7. As p → 1

−

, i.e., approaching the linear equation, the smoothness of TWs at

the interface point y = 0 increases (to C

∞

at p = 1). This mimics analytic TWs for

p = 1, where no ﬁnite propagation is available.

For conservative Boussinesq-type models

= (−1)

m+1

u − D

(|u|

p−1

u), 1 ≤ k < m,

(for m = 2, k = 1, it is the signed B(1, p) dispersive Boussinesq equation, [496]),

we have ﬁnite interfaces for TWs for k < m (see explicit nonnegative compactons

in [581] for m = 2, k = 1) and solutions of changing sign for k ≤ m − 2 with the

behavior (5.51), where 2m is replaced by 2(m − k).

Example 5.13 (A breather on invariant subspace for a cubic operator) Consider

now another cubic wave equation

= F[u] ≡ 2u

− u(u

)

+ u

. (5.52)

Such hyperbolic PDEs describe short-wave excitations of a nonlinear model, where

each atom in a 1D lattice interacts with its neighbors by anharmonic forces, [349].

252 Exact Solutions and Invariant Subspaces

Note that operator F is not potential in L

.The2π-periodic breather is given by

∗

(x , t) = C(t) cos x , where C



=−C

. (5.53)

Clearly, the ODE for C(t) has periodic solutions. Taking a single hump of cos x in

(5.53) gives a solution of the Dirichlet problem for (5.52), where



, t



= 0fort ≥ 0,

so, unlike the compact breather (5.20), this is not a solution of the Cauchy prob-

lem. The operator in (5.52) has the advantage to admit the 3D subspace W

L{1, cos x , sin x }; see Proposition 1.30, operator F

. Therefore, there exist exact so-

lutions on its 2D restriction W

= L{1, cos x },

u(x , t) = C

(t) + C

(t) cos x, (5.54)





= (C

− C



= (C

− C

This DS exhibits a ﬁnite-dimensional evolution around the breather (5.53) that de-

scribes the periodic motion on the 1D invariant subspace W

= L{cos x}, with

(t) ≡ 0 in (5.54).

5.3 Quenching and interface phenomena, compactons

5.3.1 Basic singularity phenomena and stability

Example 5.14 (Quenching, stability, and interfaces) In order to describe singu-

lar quenching phenomena in quasilinear hyperbolic models, we introduce a simple

equation combining the wave operator from (5.1) and a constant absorption term.

This leads to a quadratic wave equation with absorption

= (uu

)

− 1. (5.55)

We take smooth bounded initial functions u(x , 0) ≥ a

> 0andu

(x , 0), and, by

classical theory of hyperbolic PDEs [550, Ch. 16], we obtain a local-in-time smooth

positive solution u(x, t) of the Cauchy problem for (5.55). In view of the constant

negative absorption term −1,we may expectthat there exists a ﬁnite time T such that

u(x , t) ﬁrst touches the singular zero level {u = 0} and ceases to exist as a classical

solution. Without loss of generality, we assume that this happens the ﬁrst time at

the origin x = 0, i.e., u(0, T ) = 0. Finally, the main (actually rather restrictive)

assumption is that the classical solution without shock waves exists on (0, T ) (or, at

least, shocks waves stay away from the extinction point x = 0).

As usual, we are interested in describing the formation of the quenching singu-

larity as x → 0andt → T

−

by using solutions on a polynomial subspace of the

quadratic operator in (5.55). We choose the simplest subspace W

= L{1, x

},so

u(x , t) = C

(t) + C

(t)x

∈ W





= 2C

− 1,



= 6C