Ferrarese G. (editor) Wave Propagation
Подождите немного. Документ загружается.


74
By
writing
down
the
transport
equation
for
the
incident
weak
discontinuity
along
C(~),
as
in
Lecture
4.it
is
possible
to
determine
its
nature
as
it
approaches P from
the
left
. Then.
using
the
fact
that
the
r
transmitted
and
5
reflected
weak
discontinuities
must
propagate
along
characteristics.
it
is
possible
to
resolve
the
jumps
across
all
characteristics
at
P
in
terms
of
the
original
system
of
equations.
the
differentiated
Rankine-Hugoniot
equation
across
D
at
P and
the
initial
discontinuities
propagating
along
the
r + s
characteristics
together
with
C(,).
Provided
the
set
of
equations
that
results
at
P
is
properly
determined
the
reflected
and
transmitted
weak
discontinuities
may be
determined.
Special
cases
arise.
like
the
coincidence
of
D
with
a
characteristic
on
either
side
at
P, and
the
fact
that
the
system
may be
exceptional
with
respect
to one
or
more
characteristic
fields.
A
general
accoUDt
of
these
ideas
is
to
be fouod
in
Jeffrey
[1].
while
attention
was drawn by
Bolllat
and
Ruggeri
[5]
to
thp
necessity
to
perturb
the
shock
speed
in
cases
where
the
interface
D
can
move.
References
[1] Lax. P. D.
Hyperbolic
Systems
of
Conservation
Laws and
the
Mathematical
Theory
of
Shock Waves.
SIAM
Regional
Conference
Series
in
Applied
Mathematics.
11.
1973.
[2]
Jeffrey.
A.
Quasilinear
Hyperbolic
Systems and Waves. Research Note
in
Mathematics.
5. Pitman
Publishing.
London.
1976.
[3] Dafermos. C. H.
Characteristics
in
Hyperbolic
Conservation
Laws.
A
Study
of
the
Structure
and
the
Asymptotic
Behaviour
of
Solutions
in
Nonlinear
Analysis
and Mechanics:
Heriot-Watt
Symposium. Vol.
1.
Research Note
in
Mathematics,
17.
Pitman
Publishing.
London. 1977.
[4]
Friedrichs.
K.
0.,
Lax. P. D. Systems
of
conservation
equations
with
a convex
extension.
Proc.
Nat.
Acad.
Sci
••
USA
68
(1971).
1686-1688.
[5]
Boillat.
G.,
Ruggeri.
T.
Reflection
and
transmission
of
discontinuity
waves
through
a shock wave.
General
theory
including
also
the
case
of
characteristic
shocks.
Proc.
Roy. Soc.
Edin.
83A (1979).
17-24.

75
Lecture
7. The Riemann Problem, Glimm's Scheme and Unboundedness
of
Solutions
1. The
Riema~~
Problem
for
a
Scalar
Equation
To
illustrate
ideas
we
consider
the
single
equation
for
the
scalar
u
already
encountered
in
connection
with
weak
solutions
in
Lecture
6,
namely:
o
or,
equivalently,
(1)
0,
The Riemann problem
for
this
equation
is
then
the
resolution
of
the
discontinuous
init
ial
data
u(x,
0)
for
for
x < 0
x > 0
where U
o
and u
l
are
two
arLitrary
constants.
More
generally,
it
may be
extended
to
include
a number
of
such
discontinuities
located
along
the
initial
line.
The
characteristics
of
(1)
are
the
curves
along
which
the
equation
may be
written
in
tne
form
(2)
du
dt
K
o •
(3)
Hence
for
x < 0
the
characteristics
are
parallel
straight
lines
with
2
slope
A • u
o
'
whereas
for
x > 0
they
are
parallel
straight
lines
with
2
slope
A • u
l
•
If
2 2 h f '
1'
f h
,.
d'
,
U
o
< u
l
t
ese
two
am~
~es
0 c
aracter~st~cs
~verge
,
as
1n
Figure
(a),
when
the
wedge shaped
region
W
is
not
traversed
by any
of
these
characteristics.
However,
if
u~
>
ui
the
two
families
of
characteristics
intersect
from
the
start,
leading
to
non-uniqueness
and
shock
formation
of
the
type
first
indicated
at
the
end
of
Lecture
1,

76
(a)
Centred
simple
wave
in
W
(b)
Shock speed
f:'
Is~k
/i.,e.
I
!
I
%
we
thus
arrive
at
the
result
that
the
condition
for
a
physically
admissible
shock
solution
lor
(1)
is
(4)
Now
(1)
is
invariant
under
the
replacement
of
x and t by aX and
at,
50
that
its
solution
depends
only
on
the
ratio
t •
x/to
The
lines
t •
const.
all
pass
through
the
origin,
and
along
them u •
const.
They
thus
fill
in
the
wedge shaped
region
W
in
(a),
and
as
they
are
characteristics
the
wave
solution
described
by them
in
W
is
called
a
centred
simple
wave.
In
this
case
the
centre
is
at
0 which
is
the
location
of
the
discontinuity
in
the
initial
data
.
Taking
the
particular
case
U
o
•
0,
u
l
• 1 and
setting
u(x,
t)
•
u(t)
in
(1)
leads
to
the
differentiable
solution
for
region
W
given
in
Lecture
6,
and
illustrated
there
by 3
Figure:
u(x,
t)
{
0
for
l
(x/ t ) I
for
x/t
< 0
for
0 s
x/t
S 1
x/t
> 1
(5)
Notice
that
the
non-physical
shock (weak
solution)
given
in
Lec!:ure 6.
namely
u
(x,
c)
{:
for
x/t
<
1/3
for
x/t
>
1/3
,
(6)

77
lies
in
region
Wand so
is
~
produced by
the
intersection
of
characteristics.
It
is
for
this
reason
that
it
is
not
physically
realisable
and so must
be
rej
ected.
A
physical
shock
occurs
in
the
situation
illustrated
in
Figure
(b)
however and emanates from
the
origin.
Using
the
initial
data
u(x,
0)
for
It < 0
for
x > 0
as a
typical
example, we
find
from
the
Rankine-Hugoniot
condition
that
A=
1/3.
Thus
in
this
case
the
resolution
of
the
initial
discontinuity
merely
involves
its
propagation
along
the
shock
line
t • 3x.
We
conclude
from
this
that
for
a
centred
simple
wave
(rarefaction
fan)
to
occur,
the
characteristics
must
diverge
from a
point,
leaving
a wedge
shaped
region
to be
filled
by
the
centred
simple
wave. A shock
will
only
occur
when
the
characteristics
converge and
intersect.
2. Riemann Problem
for
a System
Let
us now
consider
the
reducible
hyperbolic
system
subject
to
the
initial
data
U(x, 0)
{
::
for
for
x < 0
x > 0 ,
(8)
where U
o
and Un
are
constant
n
element
vectors.
The Riemann problem now
becomes
the
resolution
of
the
initial
vector
discontinuity
at
x •
0,
though
as
with
the
scalar
case
it
may be
extended
to
include
a number
of
such
discontinuities
along
the
initial
line.
We
look
for
the
solution
of
this
problem
in
terms
of
generalized
simple
waves and shocks, which
will
be
the
analogue
of
the
situation
just
discussed
for
a
single
equation.
The
generalized
Rankine-Hugoniot
condition
is
of
the
form
A[
U])
[
F])
, (9)

78
once (7) has been
expressed
in
the
conservation
form
3U +
~
(U)
•
O.
3t
ax
(10)
This
implies
n
possible
types
of
shock
with
speeds
~(I)C;
•••
~A(n)
and we
shall
need a
p~1sical
admissibility
criterion
for
them,
just
as
we
did
in
the
simpler
case.
The
extension
of
our
earlier
result
(4)
that
provides
the
criterion
we need
is
due
to
Lax
Who
requires
that
for
some
integer
k
with
I S k
~
n
while
This
condition
ensures
that
k
characteristics
converge
onto
the
(11)
shock
line
from
the
left
and n - k + 1 from
the
right.
There
is
thus
a
total
of n + 1
conditions
provided
by
characteristics
which when
taken
together
with
the
n - 1
results
that
follow
from (9)
after
A
has
been
eliminated
enab
le
the
determination
of
the
2n
values
taken
by U on
the
left
(
t)
and
right
(r)
of
the
shock. The shock
that
satisfies
(11)
for
some
index k
is
called
a
k-shock.
Now
differentiable
solutions
to
system
(7)
are
also
expressible
in
terms of
the
ratio
t •
x/t,
so
that
this
system
permits
a
generalisation
of
the
notion
of
a
centred
simple
wave. The
general
solution
to
the
Riemann problem
(7),
(8)
thus
consists
of
n
fans
of
waves,
each
consisting
of
shocks and
centred
simple
waves,
arranged
in
order
of
increasing
k
from
left
to
right,
and
separated
by
sectors
in
Which
the
solution
assumes
constant
values.
As
already
mentioned,
this
generalisation
of
the
Riemann problem
may be
extended
to
the
case
of
an
initial
vector
that
is
piecewise
constant
along
the
line
t • O.
It
is
this
very
idea
that
is
basic
to
Glimm's method
for
the
numerical
solution
of
conservation
laws
(7)
with
arbitrary
initial
da
ta
in
place
of
(8),
and
it
is
this
that
forms
our
next
topic.

79
3. Glimm's Method
This
is
a method
for
the
numerical
solution
of
a system
of
hyperbolic
conservation
laws
au
+
aF
(u)
at
ax
o
(12)
with
arbitrary
initial
data
U(x,
0)
t(x)
•
(13)
It
is
a method of
first
order
in
accuracy
and
the
basic
idea
is
to
replace
the
arbitrary
initial
data
(13) by a
piecewise
constant
approxima-
tion
in
spatial
intervals
of
length
h. Then,
until
such
time
as
the
centred
simple
waves and shocks
that
result
from
the
discontinuities
interact,
an
analytical
solution
to
the
piecewise
constant
approximation
to
the
,
initial
data
is
provi~ed
by
the
solution
to
the
appropriate
Riemann problem.
If
this
solution
is
used
for
a
suitably
small
time
step
k, a new Riemann problem may be
derived
from
the
analytical
solution
at
time
't ..
k,
and
thereafter
the
process
may be
repeated
to
advance
the
solution
step
by
step
in
time
.
The
special
feature
in
Glimm's method
lies
in
the
way
in
which
the
new Riemann problem
is
derived
from
the
analytical
solution.
Unlike
the
averaging
process
over
the
spatial
interval
h
used
by
Godunov
who
also
employed
the
Riemann problem
approximation,
Glimm
chose
the
constant
value
for
each
interval
of
length
h by random sampling
within
that
interval.
Let
us
elaborate
on
this
process
sufficiently
for
its
basic
ideas
to
become
clear.
First.
however, we need to
recall
the
notion
of
a
domain
of
dependence.
In
Lecture
1.
when
discussing
a second
order
wave
equation,
the
domain of dependence
of
a
point
P was
defined
as
the
interval
produced on
the
initial
line
by
tracing
backwards
in
time
the
two
characteristics
passing
through
P
until
such time as
they
intersected
the
initial
line.
Only
data
on
this
interval
influenced
the
solution
at
P.
Now.
in
the
case
of
systems
(12).
the
analogue
is
to
trace
backwards
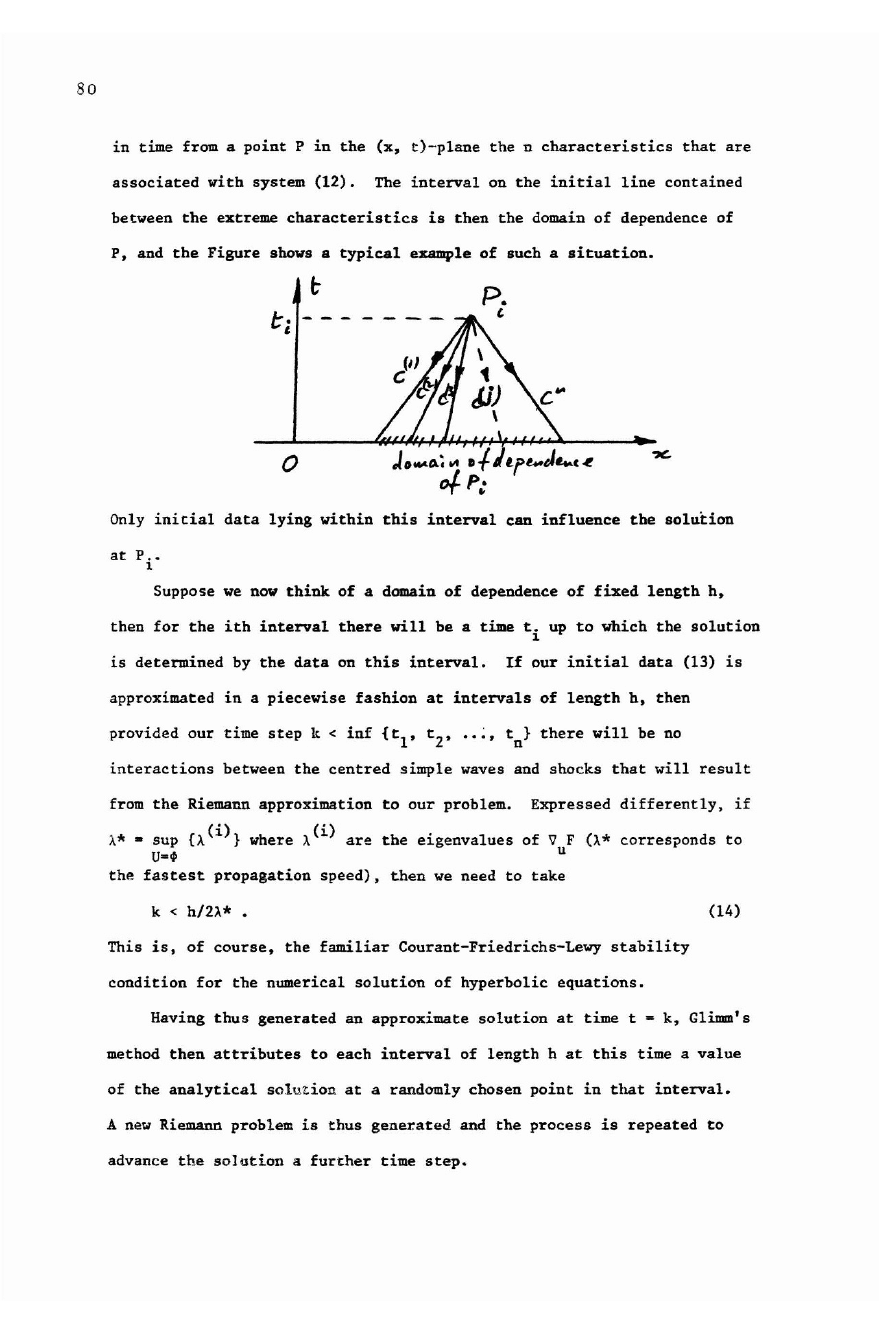
80
in
time from a
point
P
in
the
(x,
t)-plane
the
n
characteristics
that
are
associated
with
system
(12).
The
interval
on
the
initial
line
contained
between
the
extreme
characteristics
is
then
the
domain
of
dependence of
P, and
the
Figure
shows a
typical
example
of
such a
situation.
o
Only
initial
data
lying
within
this
interval
can
influence
the
solution
at
P. •
1
Suppose we now
think
of
a domain
of
dependence
of
fixed
length
h,
then
for
the
ith
interval
there
will
be a time t
i
up
to
which
the
solution
is
determined
by
the
data
on
this
interval.
If
our
initial
data
(13)
is
approximated
in
a
piecewise
fashion
at
intervals
of
length
h,
then
provided
our
time
step
k <
inf
{t
l,
t
2,
••
;,
t
n}
there
will
be no
interactions
between
the
centred
simple
waves and sho
cks
that
will
result
from
the
Riemann
approximation
to
our
problem.
Expressed
differently,
if
A* • sup
{A(i)}
where
A(i)
are
the
eigenvalues
of
V F (A*
corresponds
to
U~
u
the
fastest
propagation
speed),
then
we need
to
take
k < h/2A* •
This
is,
of
course,
the
familiar
Courant-Friedrichs-Lewy
stability
condition
for
the
numerical
solution
of
hyperbolic
equations.
(14)
Having
thus
generated
an
approximate
solution
at
time
t •
k,
Glimm's
method
then
attributes
to
each
interval
of
length
h
at
this
time a
value
of
the
analytical
sol
u
tio
n
at
a randomly chosen
point
in
tl~t
interval.
A new Riemann problem
is
thus
gener.ated and
the
process
is
repeated
to
advance
the
solution
a
further
time
step.

81
Symbolically,
if
the
subintervals
are
I
s
then
we
set
(sh,
(s + 1)
h)
,
(15)
(16)
for
x (
Is,
where un
(x,
t)
is
the
exact
solution
in
the
nth
strip
t
n
~ t
< t and
{~
}
is
a sequence
of
random numbers
havino
a
uniform
-
n+l'
n
-0
distribution
in
the
interval
(0,
1).
Let
us
use
an example due
to
Lax
to
illustrate
how
the
method liOrks
in
the
case
of two
constant
states
"t, and
~
(';.
>
~)
separated
by
a
shock moving
with
speed
~,
which
bas
the
solution
u(x,
t)
•
[~
for
for
x <
At
x>
At
(17)
For
ease
of
illustration,
let
us
take
all
time
steps
equal
and
denote
them by
k.
The
first
step
of
Glimm's scheme
gives
[~
for
for
(18)
where now
J •
1
[:
1£
1£
(19)
The
result
of
n
such
steps
with
the
scheme
is
to
give
un(x,nk) •
where we have
set
[~
for
for
x < J h
n
(20)
Ak
I
n
• number
of
Q
j
< 11 '
(21)
The law
of
large
numbers
tells
us,
with
probability
1,
I
n
•
ni(*)
+ nd
n
(22)

82
where
d
n
O(l/Iii") •
(23)
The
consequence
is
that
(20)
differs
from
the
exact
solution
(17)
by
the
error
d
n
in
the
location
of
the
shock,
though
the
discontinuity
itself
is
represented
perfectly
sharply
as
a
true
shock.
By
employing
stratified
sampling
,
Chorin
has
obtained
more
accurate
results
t han by
the
simple
random
sequences
proposed
by
Glimm
.
4.
Non-Global
Existence
of
Solutions
We
conclude
this
lecture
by
presenting
two
simple
examples
that
show
how even when a
hyperbolic
system
is
in
the
form
of
a
set
of
conservation
laws,
and
it
has
so weak a
nonlinearity
that
it
is
completely
exceptional
(also
called
linearly
degenerate
in
some
papers),
the
solution
itself
may
still
become unbounded
within
a
finite
time.
When
this
happens
no
extension
of
the
solution
is
possible,
so
that
a
global
solution
no
longer
exists
.
Consider
the
system
proposed
by
Jeffrey
o and
av
+
.&i!!L
au
_
0,
at
f(v)
ax
subject
to
the
initial
data
u(x,O)
and
v(x,O)
This
is
easily
seen
to
be
hyperbolic,
and
as
the
eigenvalues
are
±l
it
follows
that
it
must
also
be
completely
exceptional.
The
characteristic
(+)
curves
belong
to
the
two
families
of
parallel
straight
lines
C -
given
by
solving
dx
dt
±l.
Defining
u =
fg(u)du
and v •
ff(v)dv
the
system
reduces
to
the
linear
hyperbolic
system
in
conservation
form
au
+
av
_ 0
at
ax
and
The
general
solution
is
simply

83
u(x,t)
• F(x +
t)
+ G(x -
t)
,
v(x,t)
•
-F(x
+
t)
+ G(x -
t)
,
with
F,G
arbitrary
differentiable
functions.
We
now
take
two
special
cases
to
illustrate
the
unboundedness
(blow-up)
of
the
solution.
Example 1
2 2
Take uO(x) • x , vO(x) •
~l,
f •
ltv
, g -
1.
Then
it
follows
that
u(x,
e)
1
-
--#
2xt-l
There
is
thus
an
eecape
time
t.
> 0
for
the
solution
v(x,t)
when
t.
•
l/2x
(x
>
0)
•
This
is
not
due
in
any way
to
the
intersection
of
characteristics
within
a
family,
for
they
are
parallel
straight
lines.
However,
in
this
case
the
initial
data
becomes unbounded
for
large
x so
that
it
might
be
considered
this
is
the
cause
of
the
unboundedness
of
the
solution.
To show
this
is
not
the
case
consider
this
next
example.
Example 2
Take uO(x)
u(x,t)
v(x,t)
2
• a
tanh
x, vO(x) -
1,
f •
l/v
and g -
1,
when we
find
f~)
[tanh(x
+ e) +
tanh(x
-
t)]
2
2+a[tanh(x+t)-tanh(x-t)]
Here
u(x,t)
remains
finite
for
all
x,t
but
v(x,t)
becomes unbounded
at
an excape time
t.
given
by
t
...
-1
tanh
In
this
case,
by making a
suitably
small,
the
deviation
of
the
initial
data
from
constant
values
may be made as
small
as
desired,
but
the
finite
escape
time
still
persists.
