Ferrarese G. (editor) Wave Propagation
Подождите немного. Документ загружается.


64
(8)
which
is
sometimes
written
~ ~
F
]]
•
I[G]~.!!.,
(9)
with
[Q]]
denoting
the
jump
in
Q
across
discontinuity
surface
SO(t).
The
arbitrary
nature
of
dS
O
also
implies
that
U+
varies
continuously
over
S.
Because
of
the
similarity
of
(8)
to a
corresponding
condition
in
gas
dynamics
this
result
will
be
called
the
generalised
Rankine-Hugoniot
condition
for
system
(1).
In
general,
~
is
~
equal
to
a
characteristic
speed
~.
Theorem 2
(Generalised
Rankine-Hugoniot
Condition)
Consider
the
conservation
system
~~
+
div
G •
H,
with
F •
F(U,~,t),
G •
G(U,~,t)
and H •
H(U,~,t).
Then,
if
this
has
a
discontinuous
solution
across
a
surface
S, on
the
adjacent
sides
±
of
S
the
solution
varies
continuously
and
is
related
by
the
jump
condition
in
wh
ich
n
is
the
normal
to S and A
is
the
normal
speed
of
propagation
of
S,
with
G+
regarded
as
a
tensor
and G
t
.
.!!.
denoting
the
scale
of
prodvct
of
G and
the
unit
vector.!!.
normal
to
S.
Definition
(Shock
Solution)
A
discontinuous
solution
to
a
system
of
equations
expressed
in
conservation
form
which
satisfies
the
generalised
Rankine-Hugoniot
condition
will
be
called
a
shock.
2.
Weak
Solutions
and Non-Uniqueness
In
the
development
of
the
concept
of
a
solution
to a
quasilinear
hyperbolic
system,
care
has
been
taken
to
distinguish
between
classical
once
differentiable
so
called
cl
solutions,
and
piecewise
differentiable
C
1
solutions
separated
by
shocks
across
which
both
U and
its
derivatives
are
discontinuous.
It
would be
desirable,
if
possible,
to
unify
these
two
types
of
solution
by
general
ising
the
whole
concept
of
a
"solution"
to
system
(1)
in
such
a way
that
strict
differentiability
and
continuity
are
no
longer
required.
This
is

65
precisely
the
motivation
underlying
the
notion
of
a weak
solution.
For
simplicity,
the
argument
that
follows
will
be
confined
to
a
scalar
equation,
but
the
extension
to a
system
may be made
without
requiring
any
essentially
new
ideas.
For
our
starting
point
we
take
the
equation
au
+
feu)
au
• 0
at
ax
'
suoject
to
the
initial
condition
(10)
u(x.O)
g(x)
(11)
and assume
that
feu)
is
a
continuous
differentiable
function
of
u. Then
the
first
point
to
notice
is
that
(10)
can
be
expressed
in
conservation
form by
defining
F(u)
to
obtain
If(U)dU •
(12)
au
+.!!. •
at
ax
o .
(13)
Let
us
consider
the
half-plane
t > 0 and
recall
that
in
general
a
unique
solution
to (10) and
(11)
will
only
exist
for
a
finite
time.
As we
have
seen
in
Section
1, a
conservation
equation
possesses
discontinuous
solutions
or
shocks,
corresponding
to a
non-unique
solution
along
an
arc.
Accordingly,
and
with
reference
now
only
to
a
general
function
f and
initial
condition
g.
let
us
consider
some
strip
0 < t < T
in
Which
the
classical
unique
C
l
solution
exists
everywhere
except
on
certain
shock
lines
across
which
the
solution
is
bounded.
Adapting
the
notation
of
Section
1 we
denote
by u_ and u+
the
limiting
values
of
u
to
the
left
and
right
of
the
shock
under
consideration,
which from Theorem 2
are
seen
to
vary
continuously
along
the
shock.
Then
the
bounded
function
u
defined
in
the
half
plane
t > 0
will
be
called
a weak
solution
of
(10)
if
in
this
half
plane
it
satisfies
the
condition
(l4)
must be a
classical
solution
wherever
it
is
cl.
66
for
every
twice
continuously
differentiable
function
w(x,t)
that
vanishes
outside
some
finite
region
in
the
half
plane
t > o. Such
functions
ware
called
test
functions
and
the
closure
of
the
region
in
which
they
are
non-
zero
is
then
known
as
the
support
of
the
test
functions.
As a
general
classical
C
l
solution
to
(10)
subject
to
(11)
has
been
found,
we
already
1
know
that
if
a weak
solution
satisfying
(14)
is
also
piecewise
C ,
then
it
1
Thus a
piecewise
C weak
solution
coincides
with
a
piecewise
cl
classical
solution,
as
would be
expected
of
any
reasonable
extension
of
the
concept
of
a
solution
.
L~t
us now show
that
there
is
a
further
common
property
shared
between
weak and
piecewise
C
l
classical
solutions.
This
is
that
a
piecewise
C
l
weak
solution
sat
isfies
the
generalised
Rankine-Hugoniot
condition
across
a
shock.
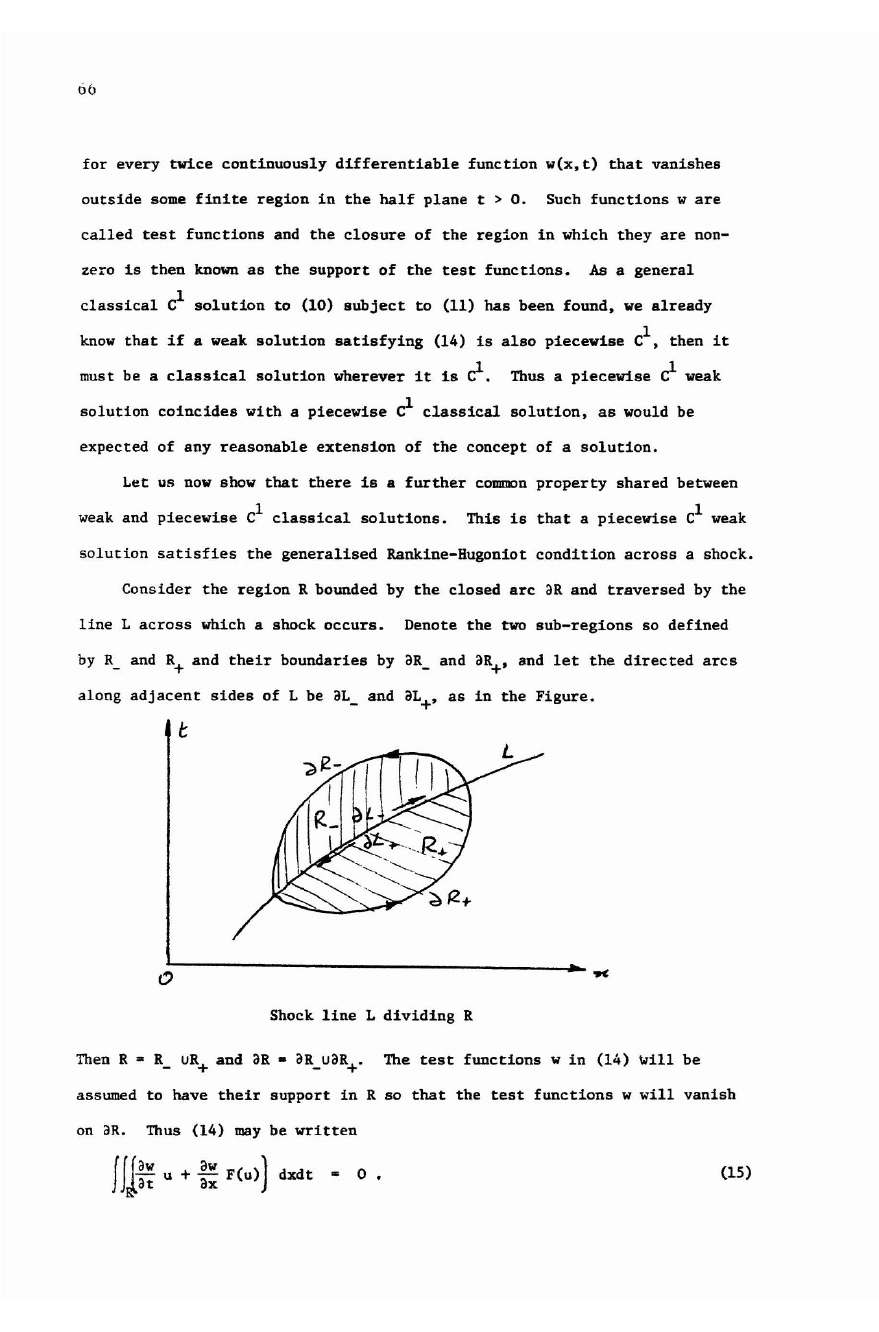
Consider
the
region
R bounded by
the
closed
arc
aR and
traversed
by
the
line
L
across
which a
shock
occurs.
Denote
the
two
sub-regions
so
defined
by
R_
and
R+
and
their
boundaries
by
aR_
and
aR+,
and
let
the
directed
arcs
along
adjacent
s
ides
of
L be aL_ and aL+,
as
in
the
Figure.
t
L
Shock
line
L
dividing
R
Then
R •
R_
UR+
and aR •
aR_UaR+.
The
test
functions
w
in
(14)
will
be
assumed to
have
their
support
in
R so
that
the
test
functions
w
will
vanish
on
oR.
Thus
(14)
may be
written
ffJ:~
u +
::
F(U»)
dxdt
o
(15)

67
Now
multiply
(13) by
wand
integrate
over
R_
to
obtain
II
R
(w
;~
+ w
;~)
dxdt
- 0 ,
which may
also
be
written
in
the
form
II
R
(a~;U)
+
a~:F»)
dxdt
-
II
R
(;~
u +
~:
F)
dxdt
• O .
(16)
Applying
Green's
theorem to
the
first
terms
in
this
result
then
transforms
(16)
to
1
-wFdt
+ wudx -
Ir(~w
u + aw F)
dxdt
•
O.
jaR
uaL
JJgt
ax
(17)
However
as
the
support
of
the
functions
w
lie
in
R, w
will
be
zero
on aR so
that
(17)
reduces
to
1
-wF(u_)dt
+ w u_dx -
Ir(aw
u +
aw
F)
dxdt
-
o.
raL
JJat
ax
A
similar
result
applies
with
respect
to R+ where we
find
f -w F(U+)
dt
+ w u+dx -
Ir(:~
u +
::
F)
dxdt
-
0,
aL+
~+
(18)
(19)
the
integration
along
aL and aL+
being
oppositely
directed,
as
indicated
in
the
Figure.
If
(18) and (19)
are
now added,
the
sign
of
the
line
integral
'in
(18)
is
reversed
with
a
corresponding
replacement
of
aL_ by aL+ and
result
(15)
is
used we
find
(20)
where
as
the
point
(x,t)
is
now
constrained
to
lie
on aL+
the
term
(dx/dt)
represents
the
speed
of
propagation
~
of
the
shock
along
L. As w
is
arbitrary,
(20)
can
only
be
true
if
(21)
which
is
the
one
dimensional
form
of
the
generalised
Rsnkine-Hugoniot
condition.
This
holds
degenerately
when u
is
continuous
across
L.
If,
now,
the
support
of
w
is
allowed
to be
arbitrary,
the
same form
of

68
argument
proves
that
piecewise
C
l
solutions
of
(13)
satisfying
(21)
across
a
shock
will
also
be a weak
solution
of
(13).
We
thus
arrive
at
the
following
definition
and
theorem.
DefInition
(Weak
Solution)
The
function
u
will
be
called
a weak
solution
of
~
+
aF(u)
_
at
ax
o
if
for
all
twice
continuously
differentiable
test
functions
w
with
support
in
t > 0
the
function
u
is
such
that
f
(raw
aw
)
J
--
u + -
F(u)
dxdt
-
lat
ax
o ,
the
integration
being
extended
over
the
upper
half
plane
t > O.
Theorem 3
(Properties
of
Weak
Solutions)
Let
u be a weak
solution
of
o .
The
following
results
are
then
true:
(a)
If
u
is
piecewise
C
l
in
addition
to
being
a weak
solution
it
is
also
a
piecewise
C
l
classical
solution.
(b) a p
iecewise
C
l
weak
solution
satisfies
the
generalised
Rankine-Hugoniot
condition
across
a
discontinuity
moving
with
speed
Aj
(c)
a
necessary
and
sufficient
condition
for
a
piecewise
cl
classical
solution
to
be a weak
solution
is
that
across
a
discontinuity
moving
with
speed
A
it
satisfies
the
generalised
Rankine-Hugoniot
condition
.
The
general
objective
when
introducing
a weak
solution
was
to
lift
the
requirements
of
strict
continuity
and
differentiability
that
need
to
be
imposed on
classical
solutions.
In
this
respect
the
notion
of
a weak
solution
is
successful
and,
furthermore,
because
of
its
method
of
definition
the
class
of
weak
solutions
is
even
wider
than
the
class
of
piecewise
C
l

69
functions
so
that
considerable
generality
has
been
achieved.
However,
this
generality
has
been
obtained
at
the
cost
of
the
uniqueness
of
a weak
solution.
More
precisely,
unlike
a
strict
classical
C
l
solution,
a weak
solution
is
not
determined
uniquely
by
the
initial
data.
This
is
most
easily
demonstrated
by means
of
a
simple
example.
Consider
a Riemann
problem
for
an
equation
of
the
form
with
ilu +.1.. (1
3}
ilt
ilx
[3 u J
-
{
Ol '
u(x,O)
-
0.
for
x < °
for
x > °
u(x,
t)
so
that
in
(13) we
have
F(u)
• u
3
/ 3.
Then, &s
the
equation
~s
homogeneous, when
it
is
differentiable
a
non-constant
solution
u
will
be a
function
of
x/t,
and
it
is
easily
verified
that
the
function
{
o
for
x/t
< °
(x/t);
for
°
~
x/t
~
I
I
for
x/t
> 1
is
a cl
solution
subject
to
the
initial
condition.
This
solution
is
continuous
everywhere
for
t >
0.
and
it
is
differentiable
everywhere
except
along
each
of
the
lines
x • °and x - t on
which,
due to
the
continuity
of
u,
the
generalised
Rankine-Hugoniot
condition
holds
in
a
degenerate
form.
It
is
a
simple
matter
to
verify
directly
that
this
piecewise
C
l
classical
solution
is
also
a weak
solution.
The form
of
this
solution
1s shown
in
the
Figure.
This
is
simply
a
centred
rarefaction
wave
of
the
type
mentioned
in
Lecture
3.
~
The
continuous
piecewise
C
1
solut
ion
resolving
a
discontinuous
initial
conditio
n.

70
Another
weak
solution
follows
by
observing
that
a
discontinuous
function
that
is
a C
l
solution
away from
the
lines
of
discontinuity
will
be a weak
solution
provided
the
discontinuity
~atisfies
the
generalised
Rank
ine-Hugoniot
condition.
L~t
us
seek
an
even
simpler
w~ak
solution
of
the
form
u(x.t)
{:
fer
x/t
< k
for
x/t
> k •
by
choosing
k
to
satisfy
the
generalised
Rankine-Hugoniot
condition.
SubB~itution
into
(2l)
coupled
with
the
fact
that
the
speed
of
shock
propagation
h .. k
then
g1ves
or
k(l
-
0)
k ..
1/3
.
(~-
0)
The
second
weak
solution
is
thus
u(x.
e)
for
x/t
<
1/3
for
x/t
>
1/3
•
and
this
weak
solution
is
piecewise
constant.
but
is
discontinous
across
the
line
3x ..
t.
In
physical
problems
only
one
solution
is
permissible.
so
that
if
the
class
of
weak
solutions
is
considered
some
selection
principle
must
be
devised
to
choose
a
unique
weak
solution
with
the
appropriate
physical
properties.
This
is
usually
achieved
on
the
basis
of
the
stability
of
the
solution
and
leads
to
selection
methods known as
entropy
conditions.
This
name
derives
from
the
gas
dynamic
case
in
which
both
compression
and
rar~faction
shocks
are
~thematically
possible.
though
only
the
compression
shock
is
physically
r~alisable
since
it
is
only
in
that
case
that
the
entropy
~es
not
decrease
,across
the
shock.
In
the
example
just
examined
the
~ed
rarefaction
wave
is
the
physical
solution
since
the
shock
wave
is
nat.
.sub.1e.

71
Some
account
of
entropy
conditions
and
of
the
associated
literature
is
to
be found
in
the
work
of
Lax
[1],
Jeffrey
[2]
and
in
the
paper
by
Dafermos
[3].
3.
Conservation
Equations
with
A Convex
Extension
When
the
conservation
system
involved
is
symmetric
hyperbolic,
the
ideas
of
Section
2 may be
pursued
in
some
detail
without
giving
rise
to
undue
difficulty.
This
we do now.
basing
our
approach
on
the
paper
by
Friedrichs
and
Lax
[4].
Consider
a system
of
conservation
equations
3U +
3G
• 0
3t
3x •
(22)
with
U and G •
G(U)
each n x 1
vectors
and
integrate
it
over
an
arbitrarily
large
interval
[-a,a]
of
the
x-axis
.
Integrating
the
second term by
parts
then
gives
rise
to
the
equation
r
au
dx
+
GI
-
GI
•
o.
at
a-a
-a
Now
for
the
class
of
solution
vectors
U
that
vanish
sufficiently
rapidly
for
large
Ixl.
so
that
G(±
a,t)
+ 0 as a + m, we
see
from
the
above
result
and
the
degenerate
form
of
Theorem I
that
showing
that
the
integral
is
a
conserved
quantity
because
it
is
independent
of
t.
The problem we now
consider
is,
when
is
a new
conservation
system
av +
aK
• 0
at
ax
•
with
V, K
functions
of
U, a
direct
consequence
of
the
original
law
(22).
To
resolve
this
we
need
to
make
a
direct
comparison between
(22)
and
(23)
(23)
lib
that
fittlt
we
perform
the
indicated
differentiations,
wben
these
equations
becOllle, rlaSp,ect:1ve1y.;

o ,
72
au
+ (V G) au .. 0
at U
ax
and
(V V)
au
+ (V K)
~
.. 0 0
U
at
U ax
Employing
the
summation
convent
ion,
the
j-th
compon
ent
of
(24) may be
written
~
+~
aUt ..
at
aUt ax
while
equation
(25)
itself
becom
es
1Y...
.-:.J
+
~
~
..
aU
j
at
aUt ax 0 0
Consequently,
comparing
(26) and (2
7),
we
conclude
th
at
(25)
will
be a
consequence
of
(26)
onl
y
if
L
et
us now
assume
that
this
cond
it
io
n
is
tru
e , and d
if
fer
ent
i
ate
i t
with
re
s pec t to
~,
when we
find
~
[ a ( av ) ) av (a
2g o
)
aUt
a
~
aU
j
+ aU
j
~
The
second
term
on
the
left
hand s i de and
th
e
right
hand
side
are
both
symmetric
in
t and h, so
that
the
f
irst
term
m
ust
al
s o be s ymmetr
ic.
~e
have
thus
shown
that
if
(28)
is
true
,
then
(24)
(25)
(26)
(27)
(28)
(30)
If,
~
fa~
[~:J)
..
~
[a:
t
[~:J)
2
now, we
multiply
(26)
by a
v/aUja~
and sum w
ith
resp
e
ct
to
j we
find
~
~+--..iL
~
aUt .. o .
~Uj
~~
at aU
j
a~
aUt ax
(29)
2
This
will
be
equivalent
to
(22)
if
the
matrix
{a
v/
aUj
a~}
is
non-singular,
and we
here
take
note
of
the
fact
that
system
(30)
is
symmetric.
Hence,
whenever
(22)
is
hyperbolic,
and
(28)
is
true,
the
equivalent
system
(30)
will
be
symmetric
hyperbolic.
It
can
be shown
that
initial
value
problems

73
for
symmetric
hyperbolic
equations
are
unique
and
will
exist
in
some
neighbourhood
of
the
initial
data.
2
As
the
hyperbolicity
of
(30)
implies
that
the
matrix
{a
v/aUja~}
is
positive
definite
we may
assert
that
V
is
a
convex
function
of
the
elements
~
and so
arrive
at
the
following
conclusion.
Theorem 4
(Uniqueness
Theorem)
If
the
system
of
conservation
equations
(22)
is
such
that
it
implies
a new
conservation
equation
(23)
with
the
property
that
the
new
conserved
quantity
V
is
a convex
function
of
the
original
elements
u
l'
u
z
' ... ,
un
of
U,
then
the
initial
value
problem
for
(2Z)
has
a
unique
solution
in
the
neighbourhood
ot
toe
initial
time.
4.
Interaction
of
Weak
Di
,continuities
We
conclude
this
lecture
by
adding
a few
remarks
about
the
interaction
ot
~
weak
discont
inui~y
propagated
along
a char ac t er i s t i c
c(~)
and a
shock.
Here we
use
the
term
weak
to
refer
to
a
solut
ion
which
is
continuous
across
C(~)
though
its
normal
derivative
i s
di
scontinuous.
This
is
in
contrast
to
the
strong
discontinuity
pf
the
Rank
ine-Hugoniot
type
wher e
the
solution
itself
is
discontinuous.
This
situation
is
illustrated
i n
the
Figure
where D
is
the
shock
line
corresponding
to
a
conservative
system
of
the
form
U
t
+ A(U)U
x
+ B(U)
~
0
/;
v
...
o
In
general
at
~where
C(~)
meets
D,
there
will
lie
r
characteristics
of
the
system
to
the
right
of
D
entering
the
state
U+ and s to
the
left
reflected
back
into
~he
state
:U~
•
