Ferrarese G. (editor) Wave Propagation
Подождите немного. Документ загружается.


34
any
explicit
dependence on
the
independent
variables
x and t . The system
(20)
will
be
quasilinear
when a
•.
e a • . (u
l•
u
2
)
and
it
will
be
linear
in
1.J 1.J
---
the
special
case
when
the
coefficients
a . .
are
all
constants.
1.J
Defining
A and U
to
be
U -
[:~J
enables
equations
(20)
to
be
written
(22)
when we know
that
the
system
will
be
totally
hyperbolic
provided
the
two
eigenvalues
A(i).
i-I.
2 of
IA-AII-O
(23)
are
real
and
distinct
and A
has
two
linearly
independent
eigenvectors.
In
place
of
the
right
eigenvectors
r
that
were
useful
in
the
previous
section.
let
us now make use
of
the
corresponding
left
eigenvectors
t
defined
t(i)
A _
A(i)
t(i)
•
for
i-I.
2.
(24)
If.
now. we
pre-multiply
(22) by
t(i)
and
use
(24) we
obtain
the
result
l(i)
(au
+
A(i)
au)
_ 0 •
at
ax
for
i-I.
2.
(25)
In
this
the
bracketed
expression
will
be
recognised
as
the
directional
derivative
of
U
with
respect
to time
along
the
family
of
characteristics
e(i).
Denoting
differentiation
with
respect
to
t ime
along
members
of
the
eel)
family
of
characteristics
by
dIdo
and
differentiation
with
respect
to
time
along
members
of
the
e(2)
family
of
characteristics
by
d/d6
enables
us
to
replace
(25) by
the
following
pair
of
ordi~ary
differential
equations
which
are
defined
along
the
ell)
characteristics
by
1
(1)
dU
cia
·0.
(26)
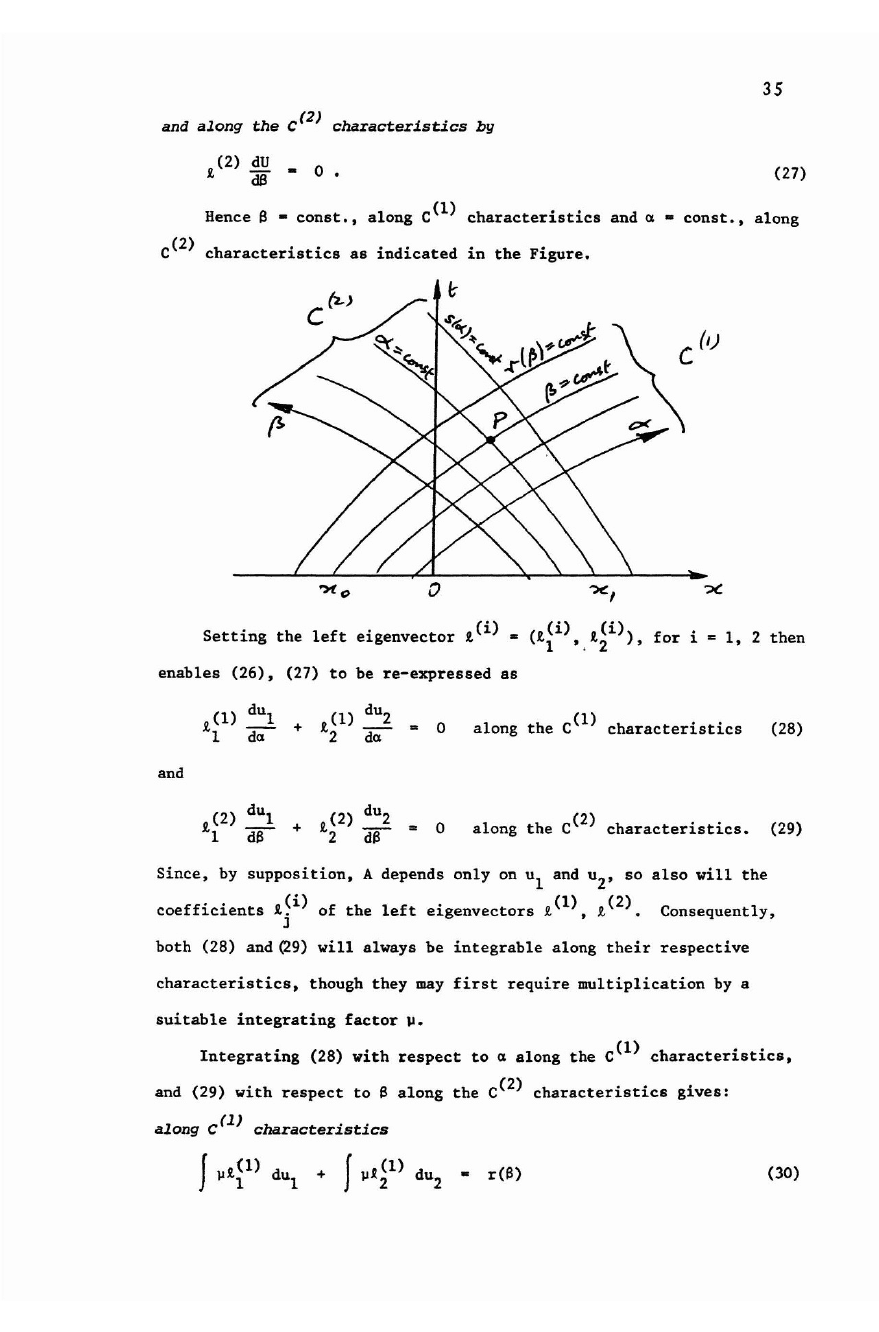
35
and
along
the
e(2)
characteristics
by
(2)
dU
II.
de
• 0
(27)
Hence B •
canst.,
along
C(l)
characteristics
and a •
canst.,
along
C(2)
characteristics
as
indicated
in
the
Figure.
Setting
the
left
eigenvector
JI.(i) •
(JI.~i),
JI.~i»,
for
i =
I,
2
then
enables
(26),
(27)
to
be
re-expressed
as
and
o
along
the
e(l)
characteristics
(28)
along
the
e(2)
characteristics.
(29)
Since,
by
supposition,
A depends
only
on u
l
and u
2'
so
also
will
the
coefficients
lI.~i)
of
the
left
eigenvectors
11.(1),
11.(2).
Consequently,
J
both
(28)
anda9)
will
always be
integrable
along
their
respective
characteristics,
though
they
may
first
require
multiplication
by a
suitable
integrating
factor
~.
Integrating
(28)
with
respect
to
a
along
the
eel)
characteristics,
and (29)
with
respect
to B
along
the
C(2)
characteristics
gives:
along
ell)
characteristics
J
(1)
J""2(1)
dU
2
~Jl.l
dU
l
+ .."
r(B)
(30)

36
and
along
C(2)
characteristics
s(a)
,
csn
where
r,
s
are
arbitrary
functions
of
their
respective
arguments
Band
a.
The two
families
of
characteristics
are
themselves
given
by
integration
of
the
equations
for
i •
1,
2.
(32)
The
functions
r(S)
and
s(a)
are
called
Riemann
invariants
and,
by
virtue
of
their
manner
of
derivation,
rand
s
are
constant
along
their
respective
families
of
characteristics.
To be more
precise,
r(s)
is
constant
along
any
C(l)
characteristic,
though as
it
is
a
function
of
S,
which
in
turn
identifies
the
characteristics,
it
will,
in
general,
be
different
for
different
characteristics.
Correspondingly,
s(a)
is
constant
along
any
c(2)
characteristic,
though
here
again
the
constant
will
be
different
for
different
characteristics
depending on
the
value
of
a
associated
with
each
characteristic.
Equations
(30) and (31)
enable
u
l
and u
2
to
be
expressed
in
terms
of
rand
s,
the
values
of
which
are
determined
at
points
of
the
initial
line
t • 0 by
the
initial
data
(21).
Suppose
r(B)
in
(30)
is
denoted
by
R(u
l,
u
2)
and
s(a)
in
(31)
is
denoted
by
S(u
l,
u
2).
Then
along
the
C(i)
characteristic
issuing
out
from
the
point
(x
O
'
0)
of
the
initial
line
in
the
sense
of
increasing
time
we have from (21) and
the
property
of
r(S)
that
(33)
Similarly,
along
the
C(2)
characteristic
issuing
out
from
the
point
(Xl'
0)
of
the
initial
line
in
the
sense
of
increasing
time we have from (21) and
the
property
of
s(a)
that
(34)

37
Solving
these
two
implicit
equations
for
u
l
and u
2
then
determines
the
solution
at
the
point
P
in
the
Figure
which
is
the
point
of
intersection
of
the
C(l)
and C(2)
characteristics
along
which
the
respective
constant
values
of
Rand
S
are
transported.
In
principle
the
initial
value
problem
is
now
solved,
since
as
the
points
(x
O'
0) and
(xl'
0) of
the
initial
line
were
arbitrary,
so
also
is
the
point
P which may be anywhere
in
tpe
upper
half
plane.
However,
in
any
particular
case,
the
task
of
solving
the
two
implicit
relationships
and
of
finding
the
characteristic
curves
in
order
to
determine
their
point
of
intersection
P
is
usually
difficult.
Nevertheless,
this
method
of
solution
can
often
be used
to
solve.problems
and
it
is,
in
any
case,
of
considerable
theoretical
importance.
References
[1]
t2]
[3]
[4]
Courant,
R.,
Friedrichs,
K. O.
Supersonic
Flow and Shock Waves,
Interscience
1948.
Jeffrey,
A.
Quasi1inear
Hyperbolic
Systems and
~aves,
Research Note
in
Mathematics, Pitman
Publishing,
London, 1976.
Coulson, C.
A.,
Jeffrey,
A. Waves, 2nd
Ed
., Longman, 1977.
Garabedian,
P. R.
Partial
Differential
Equations,
Wiley, 1964.

38
Lecture
3. Simple Waves and
the
Exceptional
Condition
1.
Simple Waves
When
one
of
the
Riemann
invariants
r
or
s
is
identically
constant,
the
corresponding
solutions
of
equations
(20)
of
Lecture
2
are
known
as
simple
wave
solutions.
That
is,
simple
wave
solutions
occur
either
when
rea)
=r
o
~
const.,
or
when
sea)
=
So
~
const.,
and we now deduce
the
basic
properties
of
this
fundamental
class
of
solutions
directly
from
this
simple
definition.
Suppose,
for
example,
that
sea)
=sO'
then
equations
(30)
and
(31)
of
Lecture
2 may be
written
rCa)
along
C(l)
characteristics
(1)
and
(2)
So
along
C
characteristics,
(2)
where
J
(i)
f
i j
(u
j
)
~R.j
du
j
•
This
shows
that
everywhere
along
a
C(l)
characteristic
specified
by
S = 8
0
=
const.,
say,
u
l
and u
2
must
also
be
constant,
for
they
are
the
sol ut i on
of
the
nonlienar
system
of
simultaneous
equations
(3)
and
The
actual
constant
values
associated
with
u
l
and u
2
along
this
characteristic
are
~
-
ul(t),
u
2
- u
2(t)
determinded
by
the
values
of
the
initial
data
(21)
of
Lecture
2
at
the
point
(~,o)
of
the
initial
line
through
which
this
eel)
characteristic
passes.
Any
function
of
u
l
and u
2
will
also
be
constant
along
this
characteristic
as,
in
particular,
will
be
A(l)(ul(~)'
u2(~»
-
A(l)(t),
say.
Consequently,
as
the
eel)
characteristic
is
found from
(32)
of
Lecture
2 by
integrating

39
C
(1)
:
:~
• II
(1)
m ,
it
D1Ust
be
the
straight
line
x •
t +
til
(1)
m
(4)
As eo and
hence
~,
were
arbitrary,
this
result
implies
that
by
allowing
~
to
move
along
its
permitted
interval
on
the
initial
line,
so
(4)
will
generate
a
straight
line
family
of
C(l)
characteristics.
Conversely,
had we
set
r(e)
_ r
O
'
it
would
then
have
followed
that
the
C(2)
family
of
characteristics
was a
family
of
straight
lines
along
each
of
which u
l
and
u
2
were
constant.
Thus
simple
waves
occur
adjacent
to
constant
state
regions
and
one
of
their
main
uses
is
to
piece
together
solutions
between
different
constant
states.
By
analogy
with
the
sit~ation
in
gas
dynamics, when a
straight
line
family
of
characteristics
converges,
the
associated
simple
wave
is
often
called
a
compression
wave,
whereas
when
it
diverges,
the
associated
simple
wave
is
called
-an
expansion
wave. Compression waves
generate
shocks
which
are
to be
discussed
later.
The
property
that
in
a
simple
wave u
l
and u
2
are
constant
along
the
straight
line
characteristics
means
that
simple
wave
solutions
are
the
simplest
type
of
npn-constant
solution
for
the
system
(1),
(2) .
2.
Generalised
Simple Waves and Riemann
Invariants
It
is
reasonable
to
enquire
whether
the
notion
of
a
simple
wave
can
be
generalised
and
extended
to
systems
with
more
than
two
dependent
variables.
Specifically
we
shall
consider
homogeneous
systems
in
one
space
dimension
and
time
of
the
type
all
(U) a
l 2
(U)
a
21
(U)
a
22
(U)
+
alo(U)
u
l
a
20
(U)
u
2
o ,
(5)
u
o t
u
n
x

~o
which
will
be
said
to
be
reducible
in
the
generalised
sense.
Since
our
concern
will
be
with
generalised
.
simple
waves we
seek
an
extension
of
a Riemann
invariant
from amongst
the
properties
of
ordinary
simple
waves. The
property
we
choose
to
generalise
is
that
in
an
ordinary
simple
wave
there
is
a
functional
dependence
between u
l
and u
2
of
the
form
u
l
z
f(u
2
) .
Accordingly.
we
propose
to
take
a
generalised
simple
wave
region
to
be one
in
which
the
solution
vector
U
is
a
function
of
only
one
of
its
n-elements,
say
of
u
1
'
so
that
U •
U(~).
If
in
(5) we
set
U - U(u
l).
so
that
u
i
•
ui(u
l)
for
i •
2,3,
. ••• n. an
elementary
calculation
establishes
that
•
o.
(6)
This
system
can
only
have
a
non-trivial
solution
if
IA- \III o •
where \I •
-(aul!at)!(aul!ax).
The n
solutions
\I(i)
to
the
algebraic
equation
(7)
are
just
the
eigenvalues
~(i)
of
A. so
that
when \I •
\I(i)
the
vector
dU!du
l
must be
proportional
to
the
right
eigenvector
rei)
of
A
corresponding
to A(i
).
As
system
(5)
is
assumed to be
hyperollc,
there
will
be n
distinct
eigenve
ctors
r(i).
The
fact
that
\I(i)
•
~(i)
then
implies
that
along
the
family
of
characteristic
curves
C(i)
dx
~
(i)
dt
•
or,
equivalently.
that
[::1)
/
(::)
(8)
aU
l
aU
l
( )
---
dx
+---
dt
• 0
along
each
member
of
the
C i
family.
ax
at
thereby
showing
that
canst.
along
each
member
of
the
C(i)
family.
(9)
A
corresponding
result
applies
along
each
of
the
n
different
families
of
characteristics
C(i).
Consider
now
the
k-th
such
family
and
let
us
determine
the
nature
of
the
generalised
simple
wave
that
is
associated
with
it.
The
fact
that
the
proposed

41
generalisation
of
a
simple
wave
region
allows
a
corresponding
generalisation
of
the
notion
of
Riemann
invariants
will
emerge from
the
fact
that
we
will
find
that
we
are
able
to
determine
the
form
of
these
generalised
invariants.
Setting
i a k
in
(9) shows
that
u
l
a
const
along
the
C(k)
family.
This
fact,
taken
together
with
U • U(u
l),
then
shows U a
const
along
members
of
the
k-th
family
of
characteristics.
As A • A(U) and U •
const
along
any C(k)
characteristic
we
conclude
that
A(k) •
const,
thereby
proving
that
the
C(k)
family
comprises
a
family
of
straight
line
characteristics.
Now
provided
attention
is
confined
to
continuous
and
differentiable
solutions,
system
(6)
may be
written
in
differential
form by
replacing
dU/du
l
by dU, when
the
fact
that
in
the
C(k)
family
of
characteristics
dU/du
l
is
proportional
to
the
right
eigenvector
r(k)
establishes
that
dU «
r(k)
along
each
member of
the
family
of
straight
line
characteristics
C(k) .
This
result
gives
rise
to
the
set
of
n
differential
equations
dU
2
"7(k)
-
r
2
in
which r
l
(k),
r
2
(k),
•••
, r
n
(k)
(10)
are
the
elements
of
the
eigenvector
r(k).
These n
first
order
ordinary
differential
equations
determine
the
behaviour
of
the
solution
U
across
what
will
be
called
a
generalised
A(k) -
simple
wave.
When
integrated,
(11)
will
give
rise
to
n-l
linearly
independent
relations
between
the
n
elements
of
U, though
multiplication
of
(10) by
an
integrating
factor
m(u
l,
u
2'
•••
, un)
might
be
necessary
because
of
the
fact
that
r(k)
is
only
determined
up
to
an
arbitrary
multiplicative
factor.
These
n-l
invariant
relations
along
the
k-th
family
of
characteristics
will
be
denoted
by
J
i
(k)(U)
-
const.for
i.
1,2,
•••
,n-l.
(11)
They
will
be
called
generalised
A(k)-Riemann
invariants
to
make
clear
that
(k)
they
are
associated
with
the
k-th
family
of
characteristics
C • These
(k)
relations
hold
throughout
the
generalised
A
-simple
wave
region
where
they
determine
the
behaviour
of
a
continuous
and
differentiable
solution.

42
On
occasions,
when
deriving
the
generalised
~(k)-Riemann
invariants
from
(10),
it
is
useful
to
express
them
in
terms
of
a
parameter
~
by
writing
(10)
in
the
form
du
n
-
---o<r
•
r
n
dt •
(12)
The u
i
may
then
be
determined
in
terms
of
t by
integrating
the
system
for
j •
l,2,
•••
,n
•
(13)
Elimination
of
t between
these
n
equations
gives
rise
to
'the
n-l
generalised
~(k)-Riemann
invariants
(11).
Definition
(Reducible
System
in
Generalised
Sense)
The
system
U + AU 0
t
X
in
which U
is
an n x 1 column
vector
and A
is
an n x n
matrix
will
be
said
to
be
reducible
in
the
generalised
sense
if
the
elements
of
A depend
explicitly
only
on U.
Definition
(Generalised
Simple
Wave
Region)
Let
the
system
in
which U
is
an n x 1 column
vector
and A
is
an n x n
matrix
be
reducible
in
the
generalised
sense.
Then any
region
S
in
the
(x ,
t)-plane
in
which
the
solution
vector
U
is
of
the
form U - U(u
j
) ,
with
u
j
one
particular
element
of
U,
will
be
called
a
generalised
simple
wave
region
.
The
following
theorem
is
easily
established
from
the
previous
results.
Theorem 1
(Generalised
Simple
Wave
Regions)
Let
the
system
U + AU 0
t X
with
U an n x 1 column
vector
and A an n x n
matrix
be
reducible
in
the
generalised
sense.
Then
if
S
is
a
generalised
simple
wave
region:

43
(a)
there
is
a
family
of
straight
line
characteristics
c(k)
traversing
S ;
(b)
the
solution
vector
U
is
constant
along
members
of
the
C(k)
family;
(c)
in
S
there
will
be
n-l
generalised
A(k)-Riemann
invariants
J
i
(k)(U)
~
const
for
i =
1,2,
•.•
,n-l
which
will
be
determined
by
integrating
equations
(10).
3.
Exceptional
Condition
and Genuine
Nonlinearity
It
is
now
appropriate
to
introduce
two
related
concepts
in
connection
with
first
order
quasilinear
hyperbolic
systems.
These
are
the
notions
of
a
solution
which
is
exceptional
with
respect
to
a
particular
characteristic
-f i el d, and
of
a
system
which
exhibits
genuine
nonlinearity
with
respect
to
a
characteristic
field.
Although
these
ideas
may be
introduced
without
reference
to
generalised
simple
waves
it
will
be
convenient
to use
this
approach
here
and to remove
this
restriction
later.
For
our
starting
point
we
and
the
associated
generalised
take
a
generalised
A(k)-Simple
wave
region
A(k)-Riemann
invariants
J
(k)(U)
•
const
i
for
i=
1,2,
.
•.
,n-l.
Each
of
these
invariants
defines
a
manifold
in
the
(u
l•
u
2
•••.•
un)-space,
on
constraint
condition
dJ (k)
i
the
i-th
of
which J (k) must obey
the
i
•
0,
or
o • (14)
(15)
(k)
Now
in
a
generalised
A
-simple
wave
region
we
have
from (13)
that
dU
j
•
r
j
(k)d~,
so
that
(14)
is
equivalent
to
the
condition
(VuJ
i
(k»r(k)
0 ,
with
i =
1.2
•.•.•
n-l.
These
orthogonality
conditions
for
the
(VuJ
i
(k»
with
respect
to
the
right
eigenvector
r(k)
associated
with
eigenvalue
A(k)
of
A
were
the
ones
used
by Lax
to
define
generalised
A(k)-Riemann
invariants.
He
then
used
this
definition
to
establish
the
properties
of
solutions
in
a
generalised
simple
wave
region
that
are
given
in
our
Theorem
1.
Before
proceeding
to
our
main
objective
let
us
first
use
condition
(
15).
together
with
an argument due to
Friedri~hs.
to
prove
that
the
solution
