Eschrig H. Topology and Geometry for Physics

Подождите немного. Документ загружается.

holds, and accordingly for more items. Equations 5.7 and 5.8 provide together a

homomorphism from the Abelian group of domains of oriented manifolds into the

Abelian group of integrals over domains of a ﬁxed form x: One even may extend

those groups and the homomorphism to real vector spaces by setting

þk

x ¼ k

x þ k

x; k

; k

2 R: ð5:9Þ

If for instance domains and integrals have a physical meaning one may think of

probability distributions over the integrals corresponding to probability distribu-

tions over domains.

Now, let U ¼fx j0 x

1; i ¼ 1; ...; ng2R

; and let w : R

! R

; m n;

be a regular embedding of a neighborhood of U 2 R

into the Euclidean space R

of possibly higher dimension. Let x be any n-form (not necessarily positive) on a

neighborhood of wðUÞ in R

: Recall, that as an embedding w is smooth and

injective and w



is injective at every point x 2 U; that is, the Jacobi matrix has

rank n (cf. p. 75). One deﬁnes now the left hand side of (5.6) as an integral over an

embedded n-dimensional manifold in R

; m n; by the right hand side which is

an integral of an n-form over the coordinate cube U in R

Let n ¼ 1 and x ¼

i¼1

ðyÞdy

a 1-form on an open subset of R

containing

wðUÞ where U is the unit interval of R and wðUÞ is a parametrized curve y ¼ wðxÞ

in R

of ﬁnite length with the curve parameter x 2 U: Then, (5.6) reads

wðUÞ

x ¼

wðUÞ

i¼1

ðyÞdy

i¼1

ðyðxÞÞ

dx:

Replacing dx by dx and integrating from x ¼ 1 to x ¼ 0 reverses also the sign of

=dx and hence the sign of the value of the integral. This is the integral over

wðUÞ: Next, ﬁx the point y

¼ wð0Þ and let s be the arc length from y

along the

curve y ¼ wðxÞ: This yields a one–one function x ¼ xðsÞ with xðSÞ¼1 where S is

the total length of the curve from y

¼ wð0Þ to y

¼ wð1Þ: Then,

wðUÞ

x ¼

i¼1

ðyðxðsÞÞÞ

ds ¼

i¼1

ðyðsÞÞ

ds;

and in this sense the integral is independent of the parametrization of the curve.

Now, assume that there is a real function uðyÞ on R

; which can be taken as a

0-form, and that x ¼ du ¼

ðou=oy

Þdy

: Then,

wðUÞ

x ¼ uðy

Þuðy

Þ; x ¼ du;

5.1 Prelude in Euclidean Space 117

which is the Fundamental Theorem of Calculus for the case of a parametrized

curve. Moreover, since x may be considered as a linear mapping of tangent vector

ﬁelds to scalar functions, the motion of a point in time t along the curve from y

t ¼ 0 to y

at t ¼ T may be considered,

wðUÞ

x ¼

i¼1

ðyðtÞÞ

dt;

where now x may be a force ﬁeld and dw=dt a velocity ﬁeld, and the integral is the

work performed on the point. Again, if the force ﬁeld x has a potential u, then

the work depends only on the potential values at the boundary points y

and y

the path.

Next, let n ¼ 2 and x ¼

1 i

m

ðyÞdy

^ dy

a 2-form on an open

subset of R

containing wðUÞ where U is the unit square of R

and wðUÞ is a

parametrized surface y ¼ wðx

; x

Þ in R

of ﬁnite area with parameters

; x

; ðx

; x

Þ2U: Then, (5.6) reads

wðUÞ

x ¼

wðUÞ

1 i

m

ðyÞdy

^ dy

1 i

m

ðyðxÞÞ

; j

¼1

1 i

m

ðyðxÞÞ





^ dx

¼1

ðyðxÞÞ

In the last equality it was used that x

is an alternating tensor.

Let u ¼

i¼1

ðyÞdy

be a 1-form and x ¼ du, that is (cf. (4.42))

x ¼

i¼1

^ dy

¼1

^ dy

1 i

m





^ dy

Inserting this expression in parentheses for x

into the last line of the integral of

the previous paragraph and using the chain rule ou

=ox

ðou

=oy

Þðow

=ox

one ﬁnds

118 5 Integration, Homology and Cohomology

wðUÞ

x ¼

i¼1





i¼1

ð1; x

Þu

ð0; x





 u

ðx

; 1Þu

ðx

; 0Þ





u 

u þ

where in the second equation integrations per part over x

in the ﬁrst item and over

in the second item were done. The terms with the second derivative of w

cancel. For the sake of simpler writing uðxÞ stands for uðyðxÞÞ: If then y

denotes

wði; jÞ; i; j ¼ 0; 1 (see Fig. 5.1), then the four terms of the integral are in fact

curvilinear integrations along the boundaries of wðUÞ as depicted in Fig. 5.1.By

observing (5.7) they constitute an integral around wðUÞ with consecutive orien-

tation in the mathematical positive sense with regard to the x

; x

-plane. Inter-

changing x

with x

would reverse this positive sense and also the sign of the

integral.

In general, the integral over an n-dimensional regularly embedded manifold in

the R

; m n; as described above of an n-form x is obtained as

wðUÞ

x ¼



1 i

\\i

m

i

ðyðxÞÞ det



^^dx



;...;i

¼1

i

ðyðxÞÞ



dx

: ð5:10Þ

What was above considered for n ¼ 1; 2,ifx ¼ du,isStokes’ theorem for the

case of a coordinate n-cube of the R

;

Fig. 5.1 The image wðUÞ of

the unit square U: For the

notation of the corners see

text

5.1 Prelude in Euclidean Space 119

wðUÞ

du ¼

owðUÞ

u; ð5:11Þ

where owðUÞ means the boundary of wðUÞ; oriented in a way in general speciﬁed

later. The boundary of a curve consists of its end points oriented outward, if the

curve is not closed (otherwise it has no boundary). To treat the Fundamental

Theorem of Calculus as the special case of Stokes’ theorem for n ¼ 1, the integral

over a point of a 0-form is deﬁned as the function value of the 0-form at that point,

provided with an appropriate sign for the orientation of that end point. For n [1

the proof goes along the same line as for n ¼ 1: The orientations of the faces are

obtained from the sign factors of (4.42) in combination with the integrations per

part. Since any n-dimensional domain can be approximated by small n-cubes, and

since cubes which touch each other by a face have this face with opposite

orientation, (5.8) shows that all the integrals over inner faces of the covering of the

domain by cubes cancel and only those of surface faces survive. Instead of cubes

less regular polyhedra can be used. This makes it evident that Stokes’ theorem

does not only hold for cubes but for any shape of domains. This will be worked out

in detail in the following sections.

As an example consider m ¼ 3 and the n-forms x

; n ¼ 0; 1; 2; 3 on R

: Let

¼ dx

n1

; n ¼ 1; 2; 3; in particular (cf. (4.42)),

i¼1

¼ðgrad x

Þdy;

1 i

3





^ dy

¼ðrot x

ÞdS;

i; j;k¼1

123

ijk

^ dy

;





^ dy

¼ðdiv XÞs;

i; j;k¼1

ijk

123

Stokes’ theorem reads in these cases

ðgrad x

Þdy ¼

¼ x

ðy

Þx

ðy

Þ;

ðrot x

ÞdS ¼

 dy;

ðdiv XÞs ¼

x  dS:

120 5 Integration, Homology and Cohomology

The ﬁrst case is the classical Fundamental Theorem of Analysis, the second case is

the classical Stokes theorem, and the third case is Gauss’ theorem.

Differential forms are the equivalents to alternating covariant tensors. Hence

they have a geometrical meaning independent of coordinate systems. The orien-

tation of an oriented manifold may be changed by a mapping, in local coordinates

expressed as ðy

; y

; ...; y

Þ!ðy

; y

; ...; y

Þ: Likewise, the orientation of R

for odd n changes by inﬂection y !y of the space coordinates. Hence, in an

odd-dimensional space, tensors of odd degree change sign of their tensor com-

ponents in an inﬂection of spatial coordinates and tensors of even degree do not.

Additionally, pseudo-tensors are introduced with reversed sign-change behavior

compared to tensors with respect to a change of orientation of space. If the above

considered n-forms x

are tensor equivalents, then obviously rot x

; dS and x are

pseudo-vectors and div X and s are pseudo-scalars. The other quantities are tensors

(including vectors and scalars). Alternatively, the x

may be understood as

pseudo-forms (pseudo-tensor equivalents), and then the roles of tensors and

pseudo-tensors in these relations are reversed. One easily checks that all the above

relations remain valid in this case. (Orientation and pseudo-character have only a

relative meaning.)

In the above examples in R

; a 2-form was related to a pseudo-vector rot x

and

a 3-form to a pseudo-scalar div X: This has a generalization to any dimension. The

Euclidean space R

is an inner product space with the standard inner product

ða jbÞ¼

i¼1

; if a

and b

are the components of the vectors a and b with

respect to an orthonormal basis ff

; ...; f

g; ðf

Þ¼d

: This inner product may

be extended to an inner product of the exterior algebra KðR

Þ by putting

ða

^^a

^^b

Þ¼detðða

ÞÞ; n m; ð5:12Þ

putting K

ðR

Þ and K

ðR

Þ orthogonal to each other for n 6¼ n

, taking the

ordinary product of numbers in K

ðR

Þ; and ﬁnally extending by bilinearity to

all KðR

Þ: Note that in case of an inner product a bilinear form on the direct

product of the space with itself is meant, not with its dual which may be a different

space. The latter case is more general and was considered in (4.20). Nevertheless,

as in (4.22),

ðf

^^ f

Þ¼d

i

j

; ð5:13Þ

where the right hand side is 1,0,or1.

W. V. D. Hodge introduced as the anticipated generalization of the above

situation the star operator or Hodge operator  : K

ðR

Þ!K

mn

ðR

Þ deﬁned

as a linear operator by

ð1Þ¼f

^^f

; ðf

^^f

Þ¼1;

ðf

^^ f

Þ¼d

i

1m

ðf

nþ1

^^ f

Þ; all 1 i

m distinct;

ð5:14Þ

5.1 Prelude in Euclidean Space 121

and extended by linearity to arbitrary exterior forms. Note that an order of the

orthonormal basis vectors f

is to be ﬁxed to deﬁne the positive orientation of R

Changing the orientation of R

; for instance by replacing f

!f

; introduces a

minus sign in the right hand side of all three deﬁning relations (5.14). In either

case it immediately follows that

 ¼ d

i

1m

nþ1

i

1m

¼ð1Þ

nðmnÞ

on base forms, if all numbers i

are distinct. (The sign is just the sign of the

permutation from the superscripts of the ﬁrst d-factor into those of the second

because for an equal order d

¼ 1 would result.) Since the right hand side is a

constant sign for each n, the result is valid in general for the application of  to an

n-form:

 ¼ ð1Þ

nðmnÞ

; ð5:15Þ

that is, up to a possible sign the Hodge operator is its own inverse. Also, since

ðR

Þ and K

mn

ðR

Þ have the same dimension, from the deﬁnition (5.14)it

follows that  is an isomorphism between these vector spaces.

On the basis of (5.13) one easily checks for two n-forms x and r

ðxjrÞ¼ðx ^rÞ¼ðr ^xÞ: ð5:16Þ

Since r is an n-form, r is an ðm nÞ-form and x ^r is an m-form which is

equivalent to the number ðx jrÞ: Let u 2 K

ðR

Þ; r 2 K

nþl

ðR

Þ and x 2 K

ðR

Þ:

Then (cf. (4.30) on p. 105), ði

r jxÞ¼ðr jL

xÞ¼ðr ju ^ xÞ: Application of the

second variant (5.16) yields ðx ^ði

rÞÞ ¼ ðu ^x ^rÞ¼ð1Þ

ðx ^u ^

rÞ for any x 2 K

ðR

Þ: Hence, since  is an isomorphism, ði

rÞ¼ð1Þ

u ^

r: With (5.15), one more application of  to this result yields

r ¼ð1Þ

nðmnlÞ

ðu ^ðrÞÞ; r 2 K

nþl

ðR

Þ; u 2 K

ðR

Þ; n þ l m:

The Hodge operator is mainly used to extend the Laplacian to manifolds

(Sect. 5.9, see also Sect. 9.6).

5.2 Chains of Simplices

In order to analyze the boundary operation in a more general context, instead of

coordinate cubes simplices as the simplest polyhedra in R

are considered and

their images in continuous or smooth mappings into manifolds, which are called

singular simplices.

Let ðv

; ...; v

Þ be r þ 1 linear independent vectors of the R

; n [ r: The set

ðv

; ...; v

Þ¼fx ¼ k

þþk

0; k

þþk

¼ 1gð5:17Þ

122 5 Integration, Homology and Cohomology

of points of the R

is an r-dimensional simplex, in short an r-simplex with vertices

: A 0-simplex is a point, a 1-simplex is a line segment, a 2-simplex is a triangle, a

3-simplex is a tetrahedron, higher dimensions are considered by analogy. For later

use, an r-simplex for any r\0 is the empty set. It is clear that

¼fx ¼ðk

; ...; k

Þjk

0; k

þþk

1gð5:18Þ

is an r-simplex (with its vertices the origin and the ﬁrst r orthonormal base vectors

of the R

) and that it is homeomorphic to any r-simplex S

ðv

; ...; v

Þ. D

is called

the standard r-simplex. It is understood as oriented by the r-form dk

^^dk

An r-simplex has r þ 1 faces, each of which is an ðr  1Þ-simplex. The faces of

ðv

; ...; v

Þ are S

r1

ðv

; ...; v

i1

; v

iþ1

; ...; v

Þ; i ¼ 0; ...; r. The faces of an

r-simplex are empty for r 0, a 1-simplex has two 0-simplices (points) as faces, a

2-simplex (triangle) has three 1-simplices (legs) as faces, a 3-simplex (tetrahe-

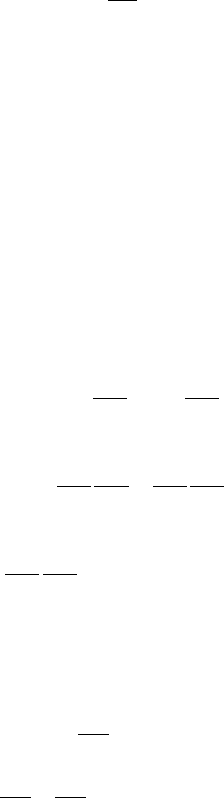
dron) has four 2-simplices (triangles) as faces, and so on. The oriented boundary

of a simplex is deﬁned as

ðv

; ...; v

Þ¼

i¼0

ð1Þ

r1

ðv

; ...; v

i1

; v

iþ1

; ...; v

Þ: ð5:19Þ

See Fig. 5.2 where oS

ðv

; v

Þ¼þS

ðv

ÞS

ðv

Þ; oS

ðv

; v

Þ¼þS

ðv

; v

Þ

ðv

; v

ÞþS

ðv

; v

Þ; and the corresponding expression (5.19) for r ¼ 3 is

visualized.

Suppose an orientation of S

ðv

; ...; v

Þ has been ﬁxed. As previously in (5.7),

the same simplex with the opposite orientation is denoted by S

ðv

; ...; v

Þ:

Obviously,

oðS

ðv

; ...; v

ÞÞ ¼ oS

ðv

; ...; v

Þ: ð5:20Þ

Moreover, like domains in (5.8), simplices may be added in which case the sums

can be understood to be unions of disjoint sets. In this sense, faces of dimension

less than r  1 are counted several times in (5.19). This will not be a problem in

the following. (In R

r1

a set of dimension less than r  1 has zero measure and

Fig. 5.2 Oriented boundaries of simplices. The þ and  signs are those of (5.19), the arrows

indicate the orientation of the faces as simplices entering (5.19)

5.2 Chains of Simplices 123

does not change integrals.) Now, let S

r1

¼ S

r1

ðv

; ...; v

i1

; v

iþ1

; ...; v

Þ and

r2

¼ S

r2

ðv

; ...; v

i1

; v

iþ1

; ...; v

j1

; v

jþ1

; ...; v

Þ; j [ i: Then,

ooS

ðv

; ...; v

Þ¼

j\i

ð1Þ

iþj

r2

i\j

ð1Þ

jþi1

r2

¼ £ : ð5:21Þ

For r [ 1, the boundary of a simplex is closed and hence its boundary is empty.

For r 1; S

r2

is by deﬁnition empty anyhow.

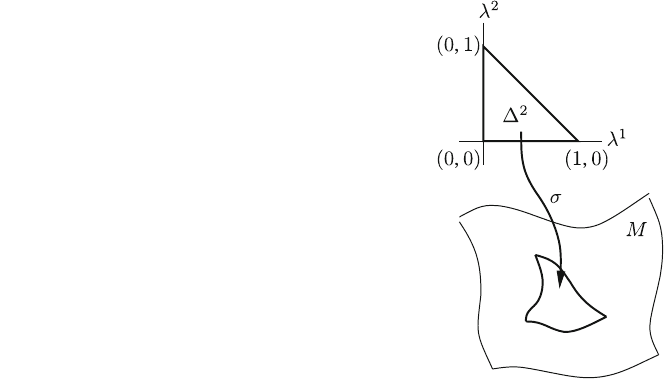
Let M be any manifold. A continuous (smooth) singular r-simplex r in M is a

continuous (smooth) mapping (of an open neighborhood in R

) of the standard

r-simplex D

into M (Fig. 5.3). M is supposed to be smooth in case of a smooth

singular r-simplex. For r\0; r is the empty mapping from the empty set into the

empty set. In order to deﬁne the boundary operation for r, ﬁrst a mapping

r1

: D

r1

! D

; i ¼ 0; ...; r,ofD

r1

onto the faces of D

must be ﬁxed. (Since

has no faces for r 0,nok

r1

for r 0 is needed.) For r ¼ 1, that is D

¼f0g

and D

¼½0; 1; k

ð0Þ¼1 and k

ð0Þ¼0: For r [ 1 one ﬁnds

r1

ðk

; ...; k

r1

Þ¼ 1 

r1

j¼1

; k

; ...; k

r1

;

r1

ðk

; ...; k

r1

Þ¼ðk

; ...; k

i1

; 0; k

; ...; k

r1

Þ; i ¼ 1; ...; r:

ð5:22Þ

r1

ðD

r1

Þ is the face of D

opposite to the origin, and k

r1

ðD

r1

Þ are the faces

with k

¼ 0 in D

(and k

of D

r1

is becoming k

jþ1

of D

for j i).

Like it was done in the last section for domains of integration, formally linear

combinations of singular simplices with integer coefﬁcients may be introduced and

usefully exploited. An r-chain of singular r-simplices r

in M is a ﬁnite linear

Fig. 5.3 A singular

2-simplex

124 5 Integration, Homology and Cohomology

combination c ¼

; k

2 Z: The set of r-chains forms the free Abelian group

generated by the set of all singular r-simplices. It can also be considered as a

Z-module. However, it turns out to be useful to allow for a ﬁeld K instead of the

ring K ¼ Z of integers. Most important besides K ¼ Z are K ¼ R and K ¼ F

;

the ﬁeld of integers modulo 2: F

¼f0; 1g; 0  0 ¼ 0; 0 1 ¼ 1; 1 1 ¼ 0; 0

0 ¼ 0 1 ¼ 0; 1 1 ¼ 1: With a ﬁeld K (R or F

), the r-chains form a vector space.

The module or vector space over K of all r-chains in M is denoted as

ðM; KÞ¼ c ¼

2 K; r

continuous singular r-simplices in Mjg;

(

ðM; KÞ¼ c ¼

2 K; r

smooth singular r-simplices in M

(

ð5:23Þ

Since for every non-trivial manifold M there is an inﬁnite set of distinct singular

simplices r, both spaces

ð0;1Þ

ðM; KÞ are in general inﬁnite-dimensional for r 0

with the distinct singular simplices forming a base. For r\0, there is no base

element, and hence

ð0;1Þ

ðM; KÞ¼f0g for r\0: ð5:24Þ

Later, the direct sum of these spaces will be treated as a grated (by r) module

(vector space).

Now, the boundary operation may be deﬁned as

o or o

ð0;1Þ

ðM; KÞ!

ð0;1Þ

r1

ðM; KÞ;

oc ¼ o

; o r ¼

i¼0

ð1Þ

r  k

r1

ð5:25Þ

If it is necessary to indicate the dimension r of the chain to which the boundary

operator is applied, the notation o

will be used. The boundary of a chain is deﬁned

as the corresponding chain of boundaries of the singular simplices, and the

boundary of a singular simplex is a chain (with integer coefﬁcients 1) formed by

ﬁrst mapping by k

r1

the standard ðr  1Þ-simplex D

r1

onto the ith face of the

standard r-simplex D

, then mapping by r this face of D

into M, and ﬁnally

linearly combining those mappings.

The standard r-simplex D

is a special case of an r-simplex S

and hence (5.21)

holds for it. It is then obvious that

o  o ¼ 0 ð5:26Þ

holds on every r-chain.

Let M be a smooth n-dimensional manifold and let the image of the r-chain c of

smooth singular simplices be part of an open set in the topology of M on which an

5.2 Chains of Simplices 125

r-form x is deﬁned, r n: By the singular r-simplex r; x may be pulled back

to D

: In a coordinate neighborhood of x ¼ rðxÞ2M; x 2 D

; that is, r ¼

ðr

ðxÞ; ...; r

ðxÞÞ; x may be given as x ¼

1\i

\\i

i

ðxÞdx

^^

: Then, with the orthonormal base in R

3 D

and the corresponding coordi-

nates k

; r



ðxÞ may be given as r



ðxÞ¼

1\i

\\i

i

ðrðxÞÞ

;...;

ðor

=ok

Þðor

=ok

Þdk

^^dk

1\i

\\i

i

ðrðxÞÞDðr

; ...; r

Þ=

Dðk

; ...; k

Þdk

^^dk

(cf. (5.2)). The integral of the r-form x over the

image of the singular r-simplex rðD

Þ in M may now be deﬁned as the ordinary

-integral of the pull-back r



ðxÞ over D

x ¼



ðxÞ for r 1;

x ¼ xðrð0ÞÞ for r ¼ 0: ð5:27Þ

The integral over an r-chain c ¼

is deﬁned as

x ¼

x: ð5:28Þ

Now, Stokes’ theorem for r-chains,

x ¼

dx; ð5:29Þ

can be proved in the general r-dimensional case, where it obviously sufﬁces to

prove it for a smooth singular r-simplex. The proof is technical but straightforward

with the above developed tools. It can be left as an exercise.

Stokes’ theorem for r-chains is the key to the deepest interrelations between

topology, algebra and analysis, the investigation of which in the middle of 20th

century, but proposed mainly by Poincaré at its beginning, was initiated by de

Rham’s theorem (Sect. 5.4).

In the above considerations, r must at least be of class C

ðR

Þ in order that

x can be pulled back. For x itself it would sufﬁce for the integral to exist that

it is a continuous r-form. However, in Stokes’ theorem x must also be C

: In

most applications both r and x may be assumed smooth. Note that in this

section, r was not assumed to be bijective; for that reason the simplices r were

called singular. For instance, r might be constant: rðD

Þ¼fxg; x 2 M: In this

case the pull back of x is the constant r-form equal to its value at x and the

integral is the volume jD

j¼1=r! of D

times this constant x: In that sense,

integrals over r-chains are still integrals in R

: Nevertheless, these constructs

are very useful. Before exploiting them, in the next section more natural

integrals which may be understood more directly over domains of manifolds

are considered.

126 5 Integration, Homology and Cohomology