Eschrig H. Topology and Geometry for Physics

Подождите немного. Документ загружается.

tðxÞ¼t

...i

...j

ðxÞ



 dx

dx

ð4:33Þ

is called a tensor ﬁeld of type ðr; sÞ on M:

The collection of all tensor ﬁelds of type ðr; sÞ on M forms again a real vector

space T

r;s

ðMÞ with respect to point wise linear combinations as is easily seen from

(4.33). It is an inﬁnite-dimensional functional vector space. It can also be con-

sidered a CðMÞ-module with respect to point wise multiplications with CðMÞ-

functions. The graded algebra of tensor ﬁelds on M is

TðMÞ¼

r;s¼0

r;s

ðMÞ: ð4:34Þ

It is a real associative but non-commutative algebra with point wise tensor mul-

tiplication as the multiplication in TðMÞ: Note that according to the deﬁnition

(4.34) a tensor ﬁeld of a certain type at some point x 2 M has the same type all

over M: For connected components of M this is a consequence of the demand of

smoothness, for distinct components of a multicomponent manifold it is just by

deﬁnition. Also, tensor contractions of tensor ﬁelds on M are deﬁned as the same

contraction performed at every point x 2 M:

An important example of a symmetric tensor ﬁeld of type ð0; 2Þ is the

Riemannian metric tensor, in a coordinate neighborhood given by gðxÞ¼

ðxÞdx

 dx

; or, as a bilinear mapping, gðX; YÞ¼g

with the properties

gðX; XÞ0; gðX; XÞ¼0; iff X ¼ 0; and gðX; YÞ¼gðY; XÞ: It deﬁnes at every

point x 2 M a scalar product and hence converts the tangent space T

ðMÞ into an

inner product space (cf. p. 19) and M into a Riemannian manifold, a concept

which is considered in more detail in Chap. 9.

An endomorphism of TðMÞ is a real linear mapping from tensor ﬁelds to tensor

ﬁelds. At every point x 2 M; it induces an endomorphism of the tensor algebra

TðT

Þ of the tangent space T

on M at that point x; which in a sense analyzed in

Chap. 7 depends smoothly on x: The endomorphism of TðMÞ is again called a

derivation, if at every x it has the properties (4.13). As an endomorphism, a

derivation of TðMÞ again vanishes applied to a constant k 2CðMÞ¼T

0;0

ðMÞ but

not in general for a function F 2CðMÞ: (An endomorphism of TðMÞ is an R-linear

mapping but not a CðMÞ-linear mapping.)

The most important derivation is the Lie derivative L

with respect to the

tangent vector ﬁeld X: From (3.15) on p. 68 it follows that for every tangent vector

ﬁeld X 2XðMÞ¼T

1;0

ðMÞ the mapping X : CðMÞ!CðMÞ : F 7!XF is a deri-

vation of T

0;0

ðMÞ¼CðMÞ: It maps F to the directional derivative of F in the

directions of the integral curves of X on M: In (3.37) on p. 82 it was shown that the

mapping X : T

1;0

ðMÞ!T

1;0

ðMÞ : Y 7!½X; Y maps similarly a tangent vector

ﬁeld Y 2T

1;0

ðMÞ to its derivatives along the integral curves of X and hence is a

derivation of T

1;0

ðMÞ¼XðMÞ: By deﬁnition, in these two cases

F ¼ XF; L

Y ¼½X; Y: ð4:35Þ

4.3 Tensor Fields and Exterior Forms 107

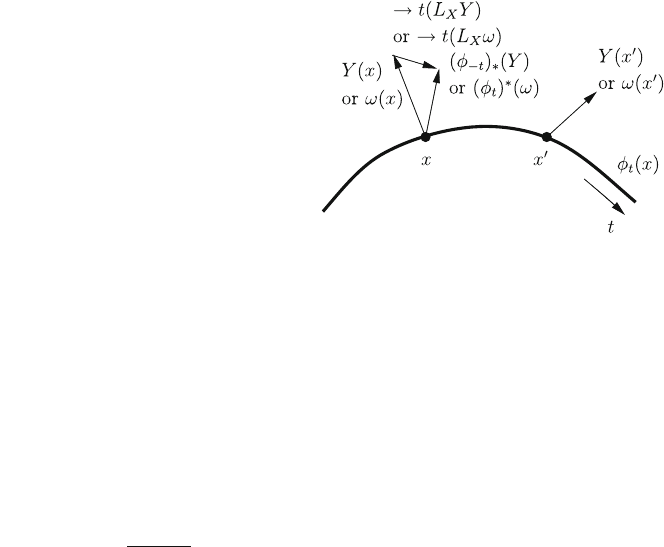
Both cases may be understood in the following way (Fig. 4.1): Fix a tangent

vector ﬁeld X on M: It deﬁnes a local 1-parameter group /

ðxÞ in a neighborhood

of every point x 2 M: Fix x and consider the (unique maximal) integral curve

ðxÞ of X through x: Push the considered entity (F or Y) forward by ð/

t



(that

is backward on the curve /

ðxÞ). This way its value originally at x

¼ /

ðxÞ is

brought to x; and there it is compared to the original value at x: A similar pro-

cedure can be applied to a cotangent vector ﬁeld x: This time it is pulled back

from x

to x by ð/



(cf. (3.28) on p. 72). Hence, a derivation may be deﬁned for

any tensor ﬁeld u 2TðMÞ as

u ¼ lim

t!0

u  u

; U

ð/

t



for tangent vector fields

ð/



for cotangent vector fields



ð4:36Þ

which declares U

for decomposable tensor ﬁelds, and then extended by linearity.

The proof that (4.36) is indeed a derivation is the same as for the product rule of

any derivative. Obviously, L

: T

r;s

ðMÞ!T

r;s

ðMÞ; and L

commutes with tensor

contractions as expressions of the type (4.36) do commute with linear combination

with constant coefﬁcients.

It is again obvious that real linear combinations and Lie products ½D; D

¼

 D

D of derivations form again derivations; the set of all derivations of

TðMÞ is a Lie algebra. Let D be a derivation of TðMÞ: As it was shown in Sect. 3.4,

its action on T

0;0

ðMÞ¼CðMÞ comes from a tangent vector ﬁeld Y and can be

localized at every point x 2 M: According to the ﬁrst relation (4.35) it may be

denoted L

and acts as a Lie derivative. Let U  M be an open set and consider all

functions F 2CðMÞ with supp F  U: A tangent vector ﬁeld X 2XðMÞ may be

said to be zero on U; if XF ¼ 0 for all those F; and supp X may be deﬁned as the

smallest closed subset of M outside of which X is zero. Now, consider the action of

any derivation D of TðMÞ on FX ¼ F  X 2T

1;0

ðMÞ¼XðMÞ: From the second

property (4.13), by arguments analogous to those in Sect. 3.4, it is seen that the

action of D on XðMÞ can be localized: supp DX  supp X: Hence, at every point

x 2 M; any derivation D of TðMÞ which vanishes on CðMÞ induces an endo-

morphism of T

ðMÞ which according to the analysis after (4.13) uniquely deﬁnes a

derivation of the tensor algebra TðT

Þ: Let D and D

coincide on CðMÞ and on

Fig. 4.1 The Lie derivative

along /

ðxÞ corresponding to

the tangent vector ﬁeld X

108 4 Tensor Fields

XðMÞ: Then, D D

vanishes there and hence vanishes on the whole TðMÞ: The

consequence is the ﬁrst part of the following theorem:

Any derivation D of TðMÞ is uniquely determined by its restrictions to

0;0

ðMÞ¼CðMÞ and to T

1;0

ðMÞ¼XðMÞ: Moreover, it has the form D ¼ L

þ S

with a uniquely determined tangent vector ﬁeld X and a uniquely determined

endomorphism S given by a tensor ﬁeld s of type ð1; 1Þ:

Proof of the second statement of the theorem Fix a derivation D of TðMÞ: The

analysis of (3.15) on p. 68 shows that every derivation of CðMÞ is provided by a

tangent vector ﬁeld X: Take this X and consider the derivation D L

of TðMÞ: It

is zero on CðMÞ: Let D

be any derivation vanishing on CðMÞ; let Y be any tangent

vector ﬁeld and F 2CðMÞ: Then, D

ðFYÞ¼FD

Y which is a linear mapping of

XðMÞ into XðMÞ and hence, according to the theorem after (4.13), it deﬁnes

uniquely a tensor ﬁeld s 2T

1;1

ðMÞ: Now, the second statement of the theorem

follows from the ﬁrst one. h

If again D is any derivation of TðMÞ and S is any tensor ﬁeld of type ð1; 1Þ;

then ½D; SF ¼ðDSÞF þ SðDFÞSDF ¼ FDS which is another tensor ﬁeld of

type ð1; 1Þ : ½D; S2T

1;1

ðMÞ for S 2T

1;1

ðMÞ: In other words, T

1;1

ðMÞ is an ideal

of the Lie algebra of all derivations of TðMÞ: Now, ½L

; L

F ¼½X; YF; and, for

Z 2XðMÞ; ½ L

; L

Z ¼½X; ½Y; Z  ½Y; ½X; Z ¼ ½½X; Y; Z due to Jacobi’s iden-

tity (3.17-3). Hence,

½L

; L

¼L

½X;Y

: ð4:37Þ

The algebra of all Lie derivatives is itself a Lie subalgebra of the Lie algebra of

all derivations of TðMÞ:

In order to ﬁnd the coordinate expressions of Lie derivatives, consider ﬁrst

ðC

1;1

ðY  xÞÞ ¼ C

1;1

ððL

YÞx þY ðL

xÞÞ which equation can be rewrit-

ten as C

1;1

ðY  L

xÞ¼XC

1;1

ðY  xÞC

1;1

ð½X; YxÞ: In a coordinate neigh-

borhood in which X ¼

ðo=ox

Þ and Y ¼

ðo=ox

Þ with g

¼ d

; with

(4.10) and (3.19) straightforwardly ðL

xÞ

¼ x

ðon

=ox

Þ is obtained. In the same

case, ðL

YÞ

¼½X; Y

¼on

=ox

results. Now, for a general tensor ﬁeld u of type

ðr; sÞ;

1;1

C

rþs;rþs

ðu  x

x

 X

X

¼ C

1;1

C

rþs;rþs

ðL

uÞx

x

 X

X

p¼1

u  x

ðL

Þx

 X

X

q¼1

u  x

x

 X

ðL

ÞX

: ð4:38Þ

4.3 Tensor Fields and Exterior Forms 109

For x

¼ dx

and X

¼ o=o x

; the left hand side of the equation (4.38)is

ðu

...i

...j

Þ¼n

...i

...j

=ox

and the ﬁrst term on the right hand side is ðL

uÞ

...i

...j

;

altogether,

ðL

uÞ

...i

...j

¼ n

...i

...j



p¼1

...i

p1

pþ1

...i

...j

q¼1

...i

...j

q1

qþ1

...j

: ð4:39Þ

It was shown in the last section that the elements of K

ðT



Þ are just the

alternating tensors of type ð0; rÞ: Hence, the sections out of K



ðMÞ are just the

alternating tensor ﬁelds of type ð 0; rÞ: They can be identiﬁed with the exterior

differential r-forms already introduced in Sect. 3.4 on p. 70. They form the real

vector space D

ðMÞ which is also a CðMÞ-module with respect to point wise linear

combinations. Their point wise exterior multiplication yields the graded exterior

algebra

DðMÞ¼

r¼1

ðMÞ; D

ðMÞ¼f0g for r\0 and r [ n ð4:40Þ

studied in Sect. 3.4.

Consider a mapping F : M ! N from the manifold M into the manifold N and

at every x 2 M its push forward (differential) as a mapping F



: T

ðMÞ!T

FðxÞ

ðNÞ

from tangent vectors on M to tangent vectors on N; given by (3.27) on p. 71. It

induces the mapping F



: DðNÞ!DðMÞ between the exterior algebras, given

point wise by (3.32) on p. 74, which pulls back any r-form on N to an r-form on

M: As it was explained in Sect. 3.5, there is no such induced mapping between the

tensor algebras TðMÞ and TðNÞ: This is why the exterior algebra of r-forms plays

such a central role in the theory of manifolds as was ﬁrst realized by E. Cartan.

Notation: The same quantity as an alternating tensor ﬁeld t or as an exterior

form x is conventionally written as

t ¼ t

...i

dx

\\i

...i

^^dx

; x

...i

¼ r!t

...i

ð4:41Þ

Not all authors use the factor r! in this connection. Check up in each case.

4.4 Exterior Differential Calculus

This is the differential calculus for the algebra DðMÞ of exterior forms on M: By

comparison of (3.25) on p. 71 with (4.28) it is seen that the exterior differen-

tiation d is an anti-derivation of degree 1 (cf. (4.26)). Its action in a coordinate

neighborhood on a general r-form (3.24) is repeated here:

110 4 Tensor Fields

dx ¼

\\i

...i

^ dx

^^dx

i;i

\\i

...i

^ dx

^^dx

rþ1

s¼1

ð1Þ

sþ1

\\i

rþ1

...i

s1

sþ1

...i

rþ1

^^ dx

rþ1

: ð4:42Þ

Any derivation or anti-derivation of DðMÞ is deﬁned by its action on the space

ðMÞ¼CðMÞ of functions F and on the space D

ðMÞ of 1-forms or differentials

dF (exercise; consider ﬁrst decomposable forms and then the linearity of the

derivation). An anti-derivation of degree 1 on DðMÞ is uniquely deﬁned by (3.25)

(see for instance [2]).

Let F : M ! N be a smooth mapping from the manifold M into the manifold N:

Then, from (3.31) it follows that for every smooth 1-form x on N the pulled back

1-form F



ðxÞ on M is smooth. Equation 3.32 shows that a general r-form on N

can be pulled back in a coordinate neighborhood according to (4.23) to a smooth

r-form on M so that the pull back F



: DðNÞ!DðMÞ is a homomorphism of

algebras. Moreover, F



commutes with d; that is,

dðF



ðxÞÞ ¼ F



ðdxÞ; x 2DðNÞ: ð4:43Þ

This holds due to (3.31) for 1-forms as the differentials of 0-forms (functions).

For the general case it is straightforwardly demonstrated using a coordinate neigh-

borhood.

From the statement proved after (4.30) on p. 105 it follows that for any vector

ﬁeld X 2XðMÞ by point wise application the interior multiplication i

ðxÞ is an

anti-derivation of degree 1 on DðMÞ: Since it is of degree 1 and D

1

¼f0g; i

yields 0 if applied to any F 2D

ðMÞ; see remark in parentheses after (4.30). On

ðMÞ; its action is given by (4.30) for the case v ¼ X and t

¼ F; which with

(3.21) and (4.10) immediately yields i

ðxÞ¼xðXÞ¼C

1;1

ðX  xÞ for any x 2

ðMÞ: The general expression is

ðxÞ¼C

1;1

ðX  xÞ¼r

i;i

\\i

...i

r1

^^dx

r1

; x 2D

ðMÞ:

ð4:44Þ

For D ¼ i

and decomposable forms, (4.28) is proved with (4.20) by Laplace’s

expansion formula for a determinant. Hence, (4.44) is the correct extension from

ðMÞ and D

ðMÞ: Since x 2D

ðMÞ is alternating,

ði

¼ 0onDðMÞð4:45Þ

follows immediately from (4.44).

4.4 Exterior Differential Calculus 111

As an example, let M ¼ R

; r ¼ d ¼ 3 and x ¼ e ¼dx

^ dx

: Then,

ðeÞ; Y ^ Zi¼e

ijk

¼ðX; Y; ZÞ ; e

ijk

¼ d

123

ijk

ðcf: ð4:22ÞÞ ; ð4:46Þ

is the triple scalar product of the vectors X; Y and Z with the components n

; g

and f

; respectively.

Finally, since for every tangent vector ﬁeld X 2XðMÞ¼T

1;0

ðMÞ the mapping

: CðMÞ!CðMÞ : F 7!XF is a derivation (of degree 0) of CðMÞ and the map-

ping L

: T

0;1

ðMÞ¼D

ðMÞ!D

ðMÞ : x 7!L

x with ðL

xÞðYÞ¼XðxðYÞÞ

xð½X; YÞ for every Y 2XðMÞ is a derivation of degree 0 of D

ðMÞ; the Lie

derivative (4.36) for alternating tensors u of type ð0; rÞ is a derivation of degree 0

of Dð MÞ:

On DðMÞ; the connection between d; i

and L

¼ d  i

þ i

 d; ½d; L

¼0; ½i

; L

¼i

½Y;X

; d

¼ 0; ði

¼ 0:

ð4:47Þ

Proof From (3.32) on p. 74 it is easily seen by operation with d on both sides that

d commutes with F



for every mapping F of manifolds. Hence, d commutes with

ð/



of (4.36) and therefore also with L

: Since i

ðMÞ¼0; for F 2D

ðMÞ the

ﬁrst equation reduces to L

F ¼ i

ðdFÞ¼dFðXÞ¼XF; which is true due to the

deﬁnition of L

: Now, let D and D

be two derivations of degree 0 of DðMÞ which

coincide on D

ðMÞ and commute with d: From ðD D

ÞF ¼ 0 and ð D  D

ÞdG ¼

dðD D

ÞG ¼ 0 one has for a general 1-form x ¼ FdG that also ðD D

Þx ¼

ððD  D

ÞFÞdG þFðD  D

ÞdG ¼ 0 and hence D and D

coincide on D

ðMÞ:

Consequently, both sides of the ﬁrst relation (4.47) coincide on D

ðMÞ and on

ðMÞ and thus on Dð MÞ (cf. remark after (4.42)). The second relation is a direct

consequence of the ﬁrst and d

¼ 0:

Again because of i

ðMÞ¼0; both sides of the third equation are zero on

ðMÞ: Now, recall that for any 1-form x and any tangent vector X; i

x ¼

xðXÞ¼C

1;1

ðX  xÞ2D

ðMÞ and L

F ¼ XF; L

Y ¼½X; Y: Then, ½i

; L

x ¼

x L

x ¼ðL

xÞðYÞL

ðC

1;1

ðY xÞÞ ¼lim

t!0

ð1=tÞðð/



x xÞðYÞð

lim

t!0

ð1=tÞC

1;1

ð/

t



Y Y



x  Y ðð/



x xÞÞ¼C

1;1

ðx lim

t!0

ð1=tÞ

ðð/

t



Y  YÞ¼C

1;1

ðx ½X; YÞ ¼  xð½X; YÞ ¼ xð½Y; XÞ ¼ i

½Y;X

x which

proves the third equation (4.47)onD

ðMÞ and hence on all DðMÞ:

The remaining two equations were considered previously and are only repeated

here for completeness. h

For an r-form x in place of the tensor u in (4.38), (4.38) and (4.24) yield

hx; X

^^X

i¼hL

x; X

^^X

p¼1

hx; X

^^½X; X

^^X

i: ð4:48Þ

112 4 Tensor Fields

With this relation and the ﬁrst equation (4.47), induction with respect to r yields

hdx; X

^^X

rþ1

p¼1

ð1Þ

pþ1

hx; X

^^X

p1

^ X

pþ1

^^X

rþ1

p\q

ð1Þ

pþq

hx; ½X

; X

^X

^^X

p1

^ X

pþ1

^^X

q1

^ X

qþ1

^^X

rþ1

i: ð4:49Þ

From (4.48) the coordinate expression of L

x is obtained in the following manner.

Put X

¼ o= o x

; then the left hand side is L

ðx

...i

Þ¼

...i

=ox

; and the

ﬁrst term on the right hand side is ðL

xÞ

...i

: In the rest use X; ðo=ox

Þ½¼



ðon

=ox

Þðo=ox

Þ: The result is

ðL

xÞ

...i

i¼1

...i

p¼1

i¼1

...i

p1

pþ1

...i

ð4:50Þ

which of course coincides with (4.39), if x is treated as an alternating tensor of

type ð0; rÞ: Observe that in the last sum the subscripts of x are not in ascending

order; ordering them introduces additional sign factors. A similar treatment of

(4.49) would make the last sum of this relation vanish since ½X

; X

 would be zero,

and the rest would just recover (4.42).

As an example the phase space X of classical point mechanics is again

considered. This 2m-dimensional manifold has a symplectic structure. A sym-

plectic structure on an even-dimensional manifold is deﬁned by a symplectic

2-form, that is a 2-form (alternating tensor ﬁeld) x which has the properties

dx ¼ 0; x

ðV; WÞ¼0 for all V 2 T

ðXÞðÞ!W ¼ 0: ð4:51Þ

Instead of diffeomorphisms of a differentiable structure, symplectomorphisms

which leave x invariant are now admitted to form the pseudo-group S:

The symplectic 2-form of the phase space X is

x ¼

i¼1

^ dp

: ð4:52Þ

Clearly dx ¼ 0; and xðV; WÞ¼

i¼1

ðv

mþi

 v

mþi

Þ¼0 for all V implies

W ¼ 0: In local coordinates x is given by the skew-symmetric 2m 2m matrix

x ¼

10



; xð V; WÞ¼V  x  W; ð4:53Þ

4.4 Exterior Differential Calculus 113

where the entries 0 and 1 are m m zero and unit matrices. Hamilton’s equations

of motion (3.40) and the Poisson brackets spell now

x ¼ dH ! W ¼ W

; f F; Gg¼i

x ¼hx; W

^ W

i; ð4:54Þ

where in a local coordinate system W

is given by (3.41) and W

correspondingly.

With the ﬁrst relation (4.47) it follows immediately from (4.54) and (4.51) that the

Lie derivative of x with respect to W

vanishes: L

x ¼ dði

xÞþi

ðdxÞ¼

H ¼ 0: This implies that the Hamiltonian ﬂow /

of the vector ﬁeld W

leaves

the symplectic form invariant:



x ¼ x: ð4:55Þ

In this context x is called the Poincaré invariant. L

is called the Liouvillian.

(Applied to real C

-functions on X it is just W

Before continuing and giving further examples of application in physics,

integration over manifolds as an important application of the exterior calculus is

treated in the next chapter.

References

1. Kobayashi, S., Nomizu, K.: Foundations of Differential Geometry. Interscience, vols. I and II.

New York (1963 and 1969)

2. Warner, F.W.: Foundations of Differentiable Manifolds and Lie Groups. Springer, New York

(1983)

114 4 Tensor Fields

Chapter 5

Integration, Homology and Cohomology

5.1 Prelude in Euclidean Space

To start from commonly familiar ground, the Euclidean space R

is considered.

Let x ¼ðx

; ...; x

Þ be Cartesian coordinates in R

so that the volume element

(measure) is s ¼ dx

dx

, a real number equal to the volume of an n-dimen-

sional brick with edge lengths dx

: In (4.17) on p. 102 it was stated that K

ðR

Þ

R and hence dx

^^dx

is equivalent to a real number. Put

s ¼ dx

dx

¼ dx

^^dx

: ð5:1Þ

Let y ¼ wðxÞ¼ðw

ðxÞ; ...; w

ðxÞÞ be arbitrary smooth coordinate functions, and

let x : wðR

Þ!R be a real (piece wise continuous) function. It is well known

from integral calculus that

wðUÞ

xðyÞdy

dy

xðwðxÞÞ

Dðw

; ...; w

Dðx

; ...; x



dx

ð5:2Þ

with the Jacobian deﬁned in (2.16). Here, dy

dy

is the volume element in the

Euclidean target space wðR

Þ of the mapping w where the y

form Cartesian

coordinates. On the other hand, considering w

as a 0-form and dw

as a 1-form on

the original R

; one has according to (4.42) and with (4.22)

^^dw

;...; j



^^dx

;...; j



j

1n

^^dx

Dðw

; ...; w

Dðx

; ...; x

^^dx

: ð5:3Þ

H. Eschrig, Topology and Geometry for Physics, Lecture Notes in Physics, 822,

DOI: 10.1007/978-3-642-14700-5_5,  Springer-Verlag Berlin Heidelberg 2011

115

together with the deﬁnition (5.1), this justiﬁes to write (5.2)as

wðUÞ

x dy

^^dy



x dy

^^dy



; ð5:4Þ

where, besides w

and dw

being treated as forms, w is also treated as a trans-

formation which pulls back x on wðR

Þ to w



ðxÞ¼x w on R

and, according to

(3.31) on p. 74, pulls back dw

to w



ðdw

Þ¼

ðow

=ox

Þdx

on the corre-

sponding cotangent spaces which in the considered Euclidean case are again

wðR

Þ and R

; respectively. U and wðUÞ are supposed to have ﬁnite volume. It is

also assumed that the w

are indexed in such an order that the Jacobian is positive.

Since dim D

ðR

Þ¼1; the expression xðwÞdw

^^dw

is the general

expression of an n-form in wðR

Þ expressed in coordinates w

,ifx is smooth. One

may consider it as a generalized volume element by giving the measure in wðR

Þ a

more ﬂexible meaning. Any n-form

x ¼ xðyÞdy

^^dy

; xðyÞ[ 0 everywhere ð5:5Þ

is called a volume form. Since it transforms from one coordinate system to

another (x being not necessarily the original Cartesian coordinates) by (5.3), a

positive n-form (5.5) remains a positive n-form under all regular coordinate

transformations with positive Jacobian. By writing the integral (5.2)as

wðUÞ

according to (5.4) any smooth transformation w yields

wðUÞ

x ¼



ðxÞð5:6Þ

with the meaning that in Cartesian coordinates (5.1) holds.

The R

is orientable (p. 60). A mapping w of a part of R

into a part of wðR

is said to preserve orientation, if the Jacobian of the mapping is positive, it reverses

orientation, if the Jacobian is negative. For two domains U and U

which contain

the same points but have reversed orientation, U

¼U is written. According to

the last expression (5.1), s

¼s in this case. Therefore,

U

x ¼

x: ð5:7Þ

If the disjoint sum of two domains U

and U

is denoted by U

þ U

; then

moreover

þU

x ¼

x þ

x ð5:8Þ

116 5 Integration, Homology and Cohomology