Eschrig H. Topology and Geometry for Physics
Подождите немного. Документ загружается.

order to distinguish this case from constraints in a totally different context con-
sidered afterwards.
The so far outlined theory presupposes that the Lagrange function L is strictly
convex in V. If as usual L has second derivatives with respect to the v
i
, this means
that for all q 2 M and for any base in T
q
(M) the symmetric m 9 m-matrix of those
second derivatives (the Hessian) has maximal rank:
rank
o
2
L
ov
i
ov
j
¼ m; det
o
2
L
ov
i
ov
j
[ 0: ð3:51Þ
This is not always the case. The theory considered now was pioneered by Dirac in
the 1950 and 1960 [8], essentially to the goal of canonical quantization of gauge
field theories (which itself is beyond the scope of the present text). With the rise of
importance of Yang-Mills theories it was a very active subject of research in the
1980 and 1990 (see, e.g. [9]), and it holds unsolved problems till now.
For the sake of simplicity of notation the theory is usually presented for a finite
number of degrees of freedom (m in our text), although corresponding systems of
that type with a finite number of degrees of freedom look rather academic.
However, the results readily transfer to fields (with a continuum of degrees of
freedom), and all gauge fields are standard cases of this transfer.
Consider, in appropriate coordinates, a Lagrange function
Lðq; VÞ¼hf ðq;
VÞ; Viþ L
ðq; VÞ;
f ¼ðf
mþ1
; ...; f
m
Þ; V ¼ðV; VÞ¼ðv
1
; ...; v
m
; v
mþ1
; ...; v
m
Þ;
rank
o
2
L
ov
i
ov
j
¼
m\m; det
o
2
L
o
v
i
ov
j
[ 0:
ð3:52Þ
Define the action integral as
S½qðtÞ; VðtÞ; PðtÞ ¼
Z
t
2
t
1
Lðq; VÞþhP; dq=dt ViðÞdt ð3:53Þ
where the P
i
; i ¼ 1; ...; m, are Lagrange multipliers for the conditions dq= dt ¼ V
along the trajectories q(t) through M. The variation with fixed end points
(q, V) yields the usual Lagrange equations of motion
dq
dt
V ¼ 0;
oL
oV
P
V¼dq=dt
¼ 0;
oL
oq
d
dt
oL
oV
V¼dq=dt
¼ 0 ð3:54Þ
with a self-explanatory vector notation of the derivatives of L (remark after 3.40).
Now, for instance,
sup
v
m
p
m
v
m
f
m
ðq; VÞv
m
no
¼
0 for
p
m
¼ f
m
ðq; VÞ
þ1 else;
ð3:55Þ
3.7 Examples from Physics 87
(exercise), and
sup
V
hP; ViLð q; VÞ
) P
oL
o
V
¼ 0 )
V ¼Vðq; P; VÞ: ð3:56Þ
From the last line of (3.52) it follows that the middle relations of (3.56) can be
resolved for
V; and for P ¼ðP; PÞ the same notation as for V was used. Inserting
the last result into f yields
p
i
¼ f
i
ðq; Vðq; P; VÞÞ ¼ f
i
ðq; PÞ; i ¼ m þ1; ...; m: ð3:57Þ
If the
V would not drop out from the functions f
i
; then obviously the rank in
(3.52) would be larger than
m: Altogether (3.38) results in
Hðq; PÞ¼
H
ðq; PÞ for P ¼ f
ðq; PÞ;
þ1 else
(
ð3:58Þ
with
H
ðq; PÞ¼hP; Vðq; PÞi L
ðq; Vðq; PÞÞ: ð3:59Þ
There are
m ¼ m m primary constraints
U
ð1Þ
i
ðq; PÞ¼p
i
f
i
ðq; PÞ¼0; i ¼ m þ1; ...; m; ð3:60Þ
for the momenta P on the trajectories.
The trajectories are now obtained from the extremum of the action integral
S
0
½qðtÞ; PðtÞ; kðtÞ ¼
Z
t
2
t
1
ðhP; dq=dtiH
ðq; PÞhU
ð1Þ
ðq; PÞ; kiÞdt; ð3:61Þ
where k
i
; i ¼ m þ 1; ...; m; are the Lagrange multipliers for the constraints. This
may be abbreviated as
S
0
¼
Z
hP; dq=dtiH
ð1Þ
ðq; P; kÞ
dt;
H
ð1Þ
ðq; P; kÞ¼H
ðq; PÞþhU
ð1Þ
ðq; PÞ; ki:
ð3:62Þ
Again with a notation q ¼ð
q; qÞ; the variation yields
dq
dt
¼
oH
ð1Þ
oP
or
dq
dt
¼
oH
ð1Þ
oP
;
dq
dt
¼ k
;
dP
dt
¼
oH
ð1Þ
oq
;
P ¼ f
: ð3:63Þ
88 3 Manifolds
The Lagrange multipliers turn out to be the velocities on the trajectories which
remained unresolved in (3.56). It is seen that the time derivative along a trajectory
of any function A(q, P) is obtained from the Poisson bracket,
Aðq; PÞ :
dA
dt
¼fH
ð1Þ
; Ag
U
ð1Þ
¼0
¼
oA
oq
;
oH
ð1Þ
oP
oH
ð1Þ
oq
;
oA
oP
U
ð1Þ
¼0
ð3:64Þ
where the constraints must be taken after the calculation of the brackets.
Note that the constraints (3.60) form a Pfaffian equation system defining an
m-
dimensional distribution in T(M). Any trajectory being solution of (3.54) must be
kept in this distribution at all times, whence the time derivatives of the constraints
should vanish,
dU
ð1Þ
dt
¼fH
ð1Þ
; U
ð1Þ
g
U
ð1Þ
¼0
¼fH
; U
ð1Þ
g
U
ð1Þ
¼0
þfU
ð1Þ
; U
ð1Þ
g
U
ð1Þ
¼0
; k
DE
¼ 0:
ð3:65Þ
Here, U
(1)
and fH
; U
ð1Þ
g are understood as cotangent vector fields on M while
fU
ð1Þ
; U
ð1Þ
g is a 2-form on M (a q-dependent antisymmetric m m-matrix in local
coordinates q
i
).
Let, as a matrix in local coordinates q
i
,
rank fU
ð1Þ
; U
ð1Þ
g
U
ð1Þ
¼0
¼ q
1
; 0 q
1
m: ð3:66Þ
As the rank of an antisymmetric matrix, q
1
is even. Then, there exist m q
1
non-
zero vector fields U
(k)
so that
fU
ð1Þ
; U
ð1Þ
g
U
ð1Þ
¼0
; U
ðkÞ
DE
¼ 0; U
ðkÞ
¼ðU
1
ðkÞ
; ...; U
m
ðkÞ
Þ; k ¼ q
1
þ 1; ...; m:
ð3:67Þ
Hence, Eq. 3.65 determines the
m linearly independent vector functions
k(q, P, t) modulo U
(k)
; a number of m q
1
linear combinations remain undeter-
mined. Instead, (3.65) comprise the conditions
fH
; U
ð1Þ
g
U
ð1Þ
¼0
; U
ðkÞ
Þ
¼ 0; ð3:68Þ
some of which may be identities, some may not be independent of the constraints
U
(1)
, but a number m
1
of them may form new constraints U
(2,1)
. Inserting the q
1
determined expressions k in terms of q, P (as well as of the suppressed variable t)
and the remaining undetermined combinations k
0
into (3.65) yields a combination
of q
1
independent expressions denoted as W
ð1Þ
ðq; P; k
0
Þ,ofm primary constraints
U
(1)
(q, P) and of m
1
new constraints U
(2,1)
(q, P). Since {H
(1)
, U
(1)
} is linear in
3.7 Examples from Physics 89
the constraints, (3.65) has a structure, with U = (U
l
) further on written as a
column,
fH
ð1Þ
; U
ð1Þ
g
U
ð1Þ
¼0
¼ 0 , K
ð1Þ
ðq; PÞ
W
ð1Þ
ðq; P; k
0
Þ
U
ð1Þ
ðq; PÞ
U
ð2;1Þ
ðq; PÞ
0
@
1
A
¼ 0; ð3:69Þ
where K
(1)
is an (m ðq
1
þ m þ m
1
ÞÞ-matrix function divided into three blocks
with rank K
ð1Þ
U
ð1Þ
;W
ð1Þ
¼ q
1
; K
ð1Þ
U
ð1Þ
;U
ð1Þ
¼ 1
m
; (unit matrix) and rank K
ð1Þ
U
ð1Þ
;U
ð2;1Þ
¼ m
1
in
an obvious block matrix notation. At the same step, introducing the determined
expressions for the k into the Hamiltonian (3.62) results in a new Hamiltonian
H
ð1Þ
1
ðq; P; k
0
Þ for which (3.65) transforms into fH
ð1Þ
1
; U
ð1Þ
g
U
ð1Þ
¼0
¼ 0: Repeating
this process with H
ð1Þ
1
ðq; P; k
0
Þ and with the new constraints results in a second step
fH
ð1Þ
1
; U
ð2;1Þ
g
U
ð1Þ
¼0
U
ð2;1Þ
¼0
¼ 0 , K
ð2Þ
ðq; PÞ
W
ð2;1Þ
ðq; P; k
00
Þ
U
ð1Þ
ðq; PÞ
U
ð2;1Þ
ðq; PÞ
U
ð2;2Þ
ðq; PÞ
0
B
B
@
1
C
C
A
¼ 0: ð3:70Þ
After a finite number of l steps there appear no new independent constraints in the
l ? 1st step although there may still remain unresolved multipliers k. (The number
of independent constraints cannot exceed the dimension of T
p
*
(M).) All constraints
U
ð2; jÞ
are called secondary constraints.
This process of ‘breeding constraints’ results in a number l ¼
m þm
1
þþ
m
k
; unique for a given Lagrange function, of constraints U, independent in the
sense that the rank of the Jacobi matrix
rank
DðUÞ
Dðq; PÞ
U¼0
¼ l: ð3:71Þ
Let (superscript t meaning the transposed, U
t
being a row)
m ¼ l rank fU; U
t
g
U¼0
: ð3:72Þ
These ranks are independent of a linear functional transformation with a ðl lÞ-
matrix V,
U
0
ðq; PÞ¼Vðq; PÞUðq; PÞ; det Vj
U¼0
6¼ 0: ð3:73Þ
There is such a transformation that
VU ¼
v
u;
; v ¼ðv
1
; ...; v
m
Þ
t
; u ¼ðu
mþ1
; ...; u
l
Þ
t
; ð3:74Þ
with
90 3 Manifolds
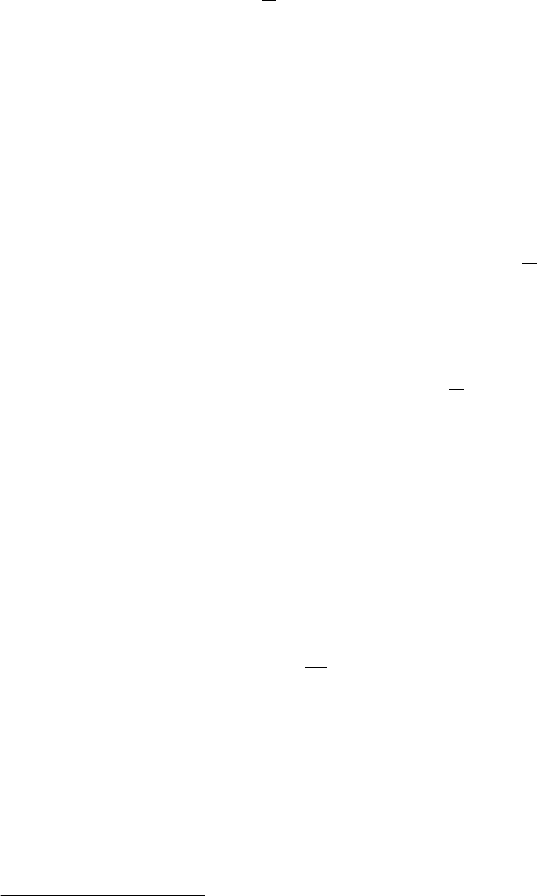
fv; Ug¼OðUÞ; det f u; ug
U¼0
6¼ 0; ð3:75Þ
where O(U) means order of U; OðUÞj
U¼0
¼ 0. The constraints ðv; uÞ¼0 are
equivalent to U = 0. The v are called first-class constraints, and the u are called
second-class constraints.
Consider first the simpler case if there are only second-class constraints.
Compared to (3.60) we subtract
m from all subscripts i of the constraints and of all
superscripts of the k in what follows. In the actually considered case, in any local
coordinate system, the matrix {U, U
t
} has maximal rank in the neighborhood of
U = 0, so that its inverse {U, U
t
}
-1
exists,
fU; U
t
g
1
fU; U
t
g¼1
l
¼fU; U
t
gfU; U
t
g
1
; ð3:76Þ
where 1
l
means the (l 9 l) unit matrix. This means that all k may be determined
from (3.65)tobe
k
k
¼
X
l
l¼1
ðfU; U
t
g
1
Þ
kl
fU
l
; H
gþOðUÞ; k ¼ 1; ...; m; ð3:77Þ
while
X
l
l¼1
ðfU; U
t
g
1
Þ
kl
fU
l
; H
g¼OðUÞ; k ¼ m þ1; ...; l: ð3:78Þ
In the equations of motion (3.64), terms of higher than first order in the U may
be added to the Hamiltonian before the Poisson brackets are calculated, since
after their calculation now all U are put to zero. One hence may define a
Hamiltonian
H
U
¼ H
U
t
fU; U
t
g
1
fU
l
; H
g; ð3:79Þ
and obtain canonical equations of motion
Aðq; PÞ :
dA
dt
¼fH
U
; Ag
U¼0
: ð3:80Þ
Alternatively, one may define Dirac’s brackets
2
instead of the Poisson brackets
by
fA; Bg
U
¼fA; BgfA; U
t
gfU; U
t
g
1
fU; Bgð3:81Þ
and have
2
Do not confuse them with Dirac’s notation of Hilbert vectors by bras and kets.
3.7 Examples from Physics 91
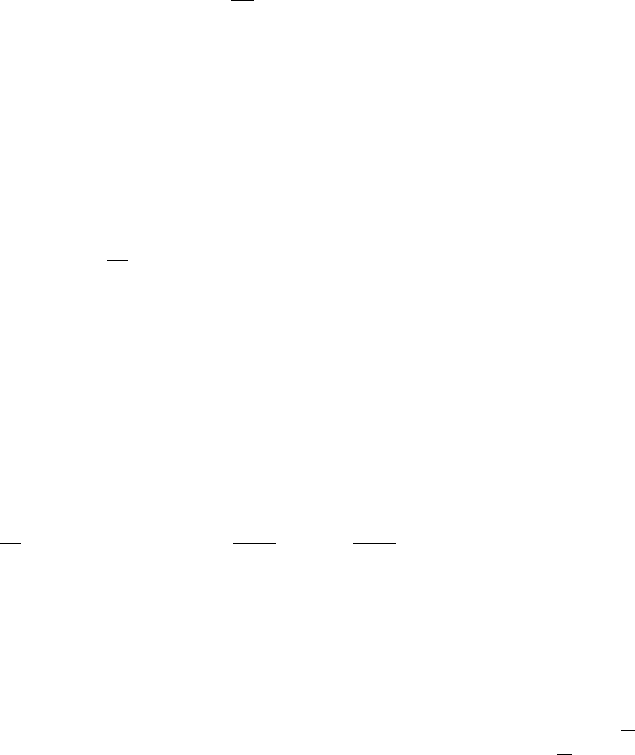
dA
dt
¼fH
; Ag
U
U¼0
: ð3:82Þ
The brackets f; g
U
have algebraic properties (3.42) like the Poisson brackets.
As the rank of the antisymmetric matrix fu; ug of (3.75) must be even, the
number of second-class constraint is always even. It can be shown [9] that a
canonical transformation from (q, P) to new canonical variables (g, /) exists so
that the g and the / separately consist of pairs of canonically conjugate variables
and the / form the constraints in the new coordinates. Then, the equations of
motion take the form
dg
dt
¼fH
/
; gg; / ¼ 0; H
/
¼ Hj
/¼0
¼ HðgÞ: ð3:83Þ
That means, the presence of only second-class constraints simply reduces the
system to an ordinary Hamilton system on a submanifold of M defined by the
distribution of the 1-forms /.
First-class constraints cannot form in Dirac’s ‘breeding’ process, if there were
no primary first-class constraints present: among first-class constraints there are
necessarily primary first-class constraints. In this case the existence of a canonical
transformation has been shown [9] to new canonical variables (g, Q, P, /)in
which the dynamics is described by the equations of motion
dg
dt
¼fH
/
; gg; P ¼ 0 ¼ /;
dQ
ð1Þ
dt
¼ k
P
ð1Þ
;
dQ
ð2Þ
dt
¼ AðgÞ; H
/
¼ Hj
ðP;/Þ¼0
;
ð3:84Þ
where P ¼ðP
ð1Þ
; P
ð2Þ
Þ; P
ð1Þ
are the primary and P
(2)
the secondary first-class
constraints, and Q are the conjugate variables to first-class constraints. A(g) are
fixed functions appearing in Dirac’s procedure, and k
P
ð1Þ
¼ k
P
ð1Þ
ðg; Q; tÞ are the
remaining undetermined Lagrange multipliers which do not enter the other
equations of motion. Hence, for any initial condition the time evolution contains
m
arbitrary functions of the canonical variables and of time t, that is, an
m-dimen-
sional class of trajectories.
The only way to save causality, which is supported by experience, is to say
that each trajectory out of this class describes the same physical process. The
k
P
ð1Þ
merely constitute redundancy in the description, for whatsoever good rea-
sons. This redundancy is conventionally called gauge freedom. Since transitions
between the trajectories of a given class can be performed one after another and
the k
P
ð1Þ
may continuously be varied, those transitions form a continuous
transformation group the elements of which are continuously connected to the
identity transformation. This is the group of gauge transformations (see
Sect. 8.3).
There is a systematic actual way to arrive at the indicated special canonical
variables which is in general, however, quite technical (see [10]).
92 3 Manifolds
3.7.4 Classical Mechanics Under Velocity Constraints
We now consider sketchily a case which was already initiated towards the end of
nineteenth century, essentially by H.R. Hertz and S.A. Chaplygin, which devel-
oped into a huge branch of Mathematical Physics and of various disciplines of
engineering over the last century, and which is a very active field of research even
today including also aspects of quantization [11].
We first switch to a much broader understanding of the configuration space
M. It may be any smooth manifold the points of which describe some mechanical
setting, for instance describing the group elements of translation and rotation
groups of rigid bodies. It may even describe the instantaneous state of some
sensor-actuator system which need not be mechanical.
Let L(q, V) be a regular Lagrange function on M,
Lðq; VÞ : det
o
2
L
ov
i
ov
j
¼ m ¼ dim M: ð3:85Þ
Let be given l \ m linearly independent smooth 1-forms f
(k)
(q)onM so that the
motion of the system is constrained by the conditions
hf
ðkÞ
; VðtÞi ¼ 0 for all t; k ¼ 1; ...; l: ð3:86Þ
According to (3.34) the f
(k)
form the annihilator D
\
of an (m - l)-dimensional
distribution D of velocity vectors. Constraints nonlinear in V are also considered in
literature, but here we limit ourselves to linear constraints. The constraints cause
constraint forces during the motion which are not (and in general cannot be)
described by the Lagrange function (3.85) and which have to be added to the
equations of motion (understood as a cotangent vector equation as previously),
d
dt
oL
oV
oL
oq
¼
X
l
k¼1
f
ðkÞ
ðqÞk
ðkÞ
ðq; tÞ¼f k; ð3:87Þ
where the coefficient functions k(q, t) are uniquely determined by the conditions
(3.86). (One has hf ; Vik ¼ 0, the constraint forces do not perform work along the
trajectories of motion; d’Alembert’s principle.) On transition to the Hamilton
function (3.38) corresponding to the Lagrange function (3.85) and adding the
constraint forces and the constraints to the canonical equations of motion one gets
dq
dt
¼
oH
oP
;
dP
dt
¼
oH
oq
þ f k; f;
oH
oP
¼ 0: ð3:88Þ
The time derivative of the constraints must be zero. The time derivative of the last
equation of (3.88) along trajectories is
o
oq
f ;
oH
oP
;
oH
oP
þ f
o
2
H
oPoP
oH
oq
þ f k
¼ 0;
3.7 Examples from Physics 93

where in the second term a second rank tensor o
2
H=ðoPoPÞ in T(M) is projected
on the 1-forms on both sides. This expression can uniquely be resolved for the k,if
f
o
2
H
oPoP
f
6¼ 0; ð3:89Þ
which condition indeed follows from (3.85) and from the linear independence of
the f
(k)
. Hence, the constraint forces are correctly determined.
If the distribution D defined by (3.86) is involutive, that is, if df
ðkÞ
^f
ð1Þ
^
^f
ðlÞ
¼ 0; k ¼ 1; ...; l, then the constraints are called holonomic. In this case the
constraints are completely integrable and the distribution of velocities D defines a
submanifold N of M as its integral manifold to which the whole motion of the
system is confined.
If D is not involutive, the constraints are called nonholonomic. The classical
example is a rolling disc without slipping on an inclined plane (Chaplygin).
Though nonholonomic motion is rather the standard case in everydays life (see the
just mentioned example) it comprises a huge in large parts unexplored field, and
even the motion of simple (but tricky) toys like the ‘rattleback’ is poorly under-
stood. There is in general a ‘bracket formulation’ of the equations of motion [12],
but the brackets do not obey property 3 of Poisson brackets, the Jacobi identity
(3.42).
3.7.5 Thermodynamics
The thermodynamic equilibrium state of a gas of N particles is described by its
volume v and temperature t. The thermodynamic phase space is M ¼ R
2
in this
case. The amount of heat put into an ideal gas is
dQ ¼ cðtÞdt þ
Rt
v
dv; ð3:90Þ
where c(t) is the heat capacity at constant volume which is a function of tem-
perature only and R is the gas constant. A change of the thermodynamic state is
called adiabatic, if no heat is exchanged, that is, if dQ = 0.
The question is, whether dQ = 0 defines uniquely paths through the phase
space. Since (3.90) is a 1-form in R
2
, dQ = 0 is a Pfaffian equation, for which
ddQ ¼ðoðRt=vÞ= o tÞdt ^ dv 6¼ 0; but since ddQ ^ dQ = 0, the equation is com-
pletely integrable (as any 1-form in two dimensions, since dx ^ x is a 3-form for
every 1-form x). Hence, the answer to the question is positive, and there is an
adiabatic flow /
s
ad
(t, v)(s 2 R is some curve parameter) through the phase space:
through every point (t, v) there is exactly one adiabatic trajectory. Consequently,
there are functions, constant on trajectories and hence invariant under the adiabatic
flow.
94 3 Manifolds
Nature or microscopic reasoning in Statistical Physics tells us, that as part of
Second Law of thermodynamics it always holds that entropy s, given by ds ¼
dQ=t is such an adiabatic invariant, that is, ds is always a total differential, and
s /
ad
¼ s:
References
1. Hartshorne, R.: Algebraic Geometry. Springer, New York (1977)
2. Kobayashi, S., Nomizu, K.: Foundations of Differential Geometry, Interscience, vols. I and
II. New York (1963, 1969)
3. Chern, S.S., Chen, W.H., Lam, K.S.: Lectures on Differential Geometry. World Scientific,
Singapore (2000)
4. Warner, F.W.: Foundations of Differentiable Manifolds and Lie Groups. Springer, New York
(1983)
5. Schwartz, L.: Analyse Mathématique. Hermann, Paris (1967)
6. Arnold, V.I., Kozlov, V.V., Neishtadt, A.I.: Dynamical Systems III. Encyclopedia of
Mathematical Sciences, vol. 3. Springer, Berlin (1988)
7. Morchio, G., Strocchi, F.: Classical and quantum mechanics from the universal Poisson-
Rinehart algebra of a manifold. Rep. Math. Phys. 64, 33–48 (2009)
8. Dirac, P.A.M.: Lectures on Quantum Mechanics. Academic Press, New York (1964)
9. Gitman, D.M., Tyutin, I.V.: Quantization of Fields with Constraints. Springer, Berlin (1990)
10. Chitaia, N.P., Gogilidze, S.A., Surovtsev, Y.S.: Dynamical systems with first- and second-
order constraints. I and II. Phys. Rev. D 56, 1135–1155 (1997)
11. Bloch, A.M., Fernandez, O.E., Mestdag, T.: Hamiltonization of nonholomorphic systems and
the inverse problem of the calculus of variations. Rep. Math. Phys. 63, 225–249 (2009)
12. van der Schaft, A.J., Maschke, B.M.: On the Hamiltonian Formulation of Nonholomorphic
Mechanical Systems. Rep. Math. Phys. 34, 225–233 (1994).
3.7 Examples from Physics 95

