Eschrig H. Topology and Geometry for Physics

Подождите немного. Документ загружается.

Basic notations

Sets A, B, ..., X, Y, ... are subjects of the axioms of set theory. A ¼fx jPðxÞg

denotes the family of elements x having the property P; if the elements x are

members of a set X, x 2 X, then the above family is a set, a subset (part) of the set

X: A , X. X is a superset of A; X  A. ;  will always be used to allow equality.

A proper subset (superset) would be denoted by A ( XðX )AÞ: Union, intersection

and complement of A relative to X have their usual meaning. The product of n sets

is in the usual manner the set of ordered n-tuples of elements, one of each factor.

Set and space as well as subset and part are used synonymously. Depending on

context the elements of a space may be called points, n-tuples, vectors, functions,

operators, or something else. Mapping and function are also used synonymously.

A function f from the set A into the set B is denoted f : A ! B : x 7!y: It maps

each point x 2

A uniquely to some point y = f (x) [ B. A is the domain

of f and f ðAÞ¼ff ðxÞjx 2 AgB is the range of f ;ifU  A; then f ðUÞ¼

ff ðxÞjx 2 Ugis the image of U under f. The inverse image or preimage U ¼

1

ðVÞA of V  B under f is the set f ðUÞ¼fx jf ðxÞ2Vg. V need not be a

subset of the range f (A); f

-1

(V) may be empty. Depending on context, f may be

called real, complex, vector-valued, function-valued, operator-valued, ...

The function f : A ? B is called surjective or onto, if f (A) = B. It is called

injective or one-one, if for each y 2 f ðAÞ, f

-1

({y}) = f

-1

(y) consists of a single

point of A. In this case the inverse function f

-1

: f (A) ? A exists. A surjective and

injective function is bijective or onto and one-one. If a bijection between A and

B exists then the two sets have the same cardinality. A set is countable if it has the

cardinality of the set of natural numbers or of one of its subsets.

The identity mapping f : A ! A : x 7!x is denoted by Id

. Extensions and

restrictions of f are deﬁned in the usual manner by extensions or restrictions of the

domain. The restriction of f : A ? B to A

, A is denoted by f j

: If f : A ? B and

g : B ? C, then the composite mapping is denoted by g f : A ! C :

x 7!gðf ðxÞÞ:

The monoid of natural numbers (non-negative integers, 0 included) is denoted

by N: The ring of integers is denoted by Z; sometimes the notation N ¼ Z

used. The ﬁeld of rational numbers is denoted by Q; that of real numbers is

denoted by R and that of complex numbers by C . R

is the non-negative ray of R:

The symbol ) means ‘implies’, and , means ‘is equivalent to’. ‘Iff’

abbreviates ‘if and only if’ (that is, , ), and h denotes the end of a proof.

xii Basic notations

Chapter 1

Introduction

Topology and continuity on the one hand and geometry or metric and distance on

the other hand are intimately connected pairs of concepts of central relevance both

in analysis and physics. A totally non-trivial concept in this connection is

parallelism.

As an example, consider a mapping f from some two-dimensional area into the

real line as in Fig. 1.1a. Think of a temperature distribution on that area. We say

that f is continuous at point x, if for any neighborhood V of y ¼ f ðxÞ there exists a

neighborhood U of x (for instance U

in Fig. 1.1a for V indicated there) which is

mapped into V by f . It is clear that the concept of neighborhood is central in the

deﬁnition of continuity.

As another example, consider the mapping g of Fig. 1.1b. The curve segment

is mapped into V, but the segment W

is not: its part above the point x is

mapped into an interval above y ¼ gðxÞ and its part below x is mapped disruptly

into a lower interval. Hence, there is no segment of the curve W

which contains x

as an inner point and which is mapped into V by g. The map g is continuous on the

curve W

but is discontinuous at x on the curve W

. (The function value makes a

jump at x.) Hence, it cannot be continuous at x as a function on the two-dimen-

sional area. To avoid conﬂict with the above deﬁnition of continuity, the curve W

must not be considered a neighborhood of x in the two-dimensional area.

If f is a mapping from a metric space (a space in which the distance dðx; x

between any two points x and x

is deﬁned) into another metric space, then it

sufﬁces to consider open balls B

ðxÞ¼fx

jdðx; x

Þ\eg of radius e as neighbor-

hoods of x. The metric of the n-dimensional Euclidean space R

is given by

dðx; x

Þ¼ð

i¼1

ðx

 x

1=2

where the x

are the Cartesian coordinates of x.It

also deﬁnes the usual topology of the R

. (The open balls form a base of that

topology; no two-dimensional open ball is contained in the set W

above.)

Later on in Chap. 2 the topology of a space will be precisely deﬁned. Intuitively

any open interval containing the point x may be considered a neighborhood of x on

the real line R (open intervals form again a base of the usual topology on R).

Recall that the product X  Y of two sets X and Y is the set of ordered pairs ðx; yÞ,

H. Eschrig, Topology and Geometry for Physics, Lecture Notes in Physics, 822,

DOI: 10.1007/978-3-642-14700-5_1, Ó Springer-Verlag Berlin Heidelberg 2011

x 2 X, y 2 Y.IfX and Y are topological spaces, this leads naturally to the product

topology in X  Y with a base of sets fðx; yÞjx 2 U; y 2 Vg where U and V are in

the base of the topology of X and Y, respectively. If this way the Cartesian plane is

considered as the topological product of two real lines, R

¼ R R, then the

corresponding base is the set of all open rectangles. (This base deﬁnes the same

topology in R

as the base of open balls.) Note that neither distances nor angles

need be deﬁned so far in R  R: topology is insensitive to stretchings or skew

distortions as long as they are continuous.

Consider next the unit circle, ‘the one-dimensional unit sphere’ S

, as a topo-

logical space with all open segments as base of topology, and the open unit interval

I ¼0; 1½ on the real line, with open subintervals as base of topology. Then, the

topological product S

 I is the unit cylinder with its natural topology. Cut the

cylinder on a line ‘above one point of S

’, turn one cut edge around by 180



and

glue the edges together again. A Möbius band is obtained (Fig. 1.2). This rises the

question, can a Möbius band be considered as a topological product similar to the

case of the unit cylinder? (Try it!) The true answer is no.

There are two important conclusions from that situation: (i) besides the local

properties of a topology intuitively inferred from its base there are obviously

important global properties of a topology, and (ii) a generalization of topological

product is needed where gluings play a key role.

(a)

(b)

Fig. 1.1 Mappings from a

two-dimensional area into the

real line. a mapping f

continuous at x, b mapping g

discontinuous at x. The

arrows and shaded bars

indicate the range of the

mapping of the sets U

, U

and parts of W

respectively

2 1 Introduction

This latter generalization is precisely what a (topological) manifold is. The unit

cylinder cut through in the above described way may be unfolded into an open

rectangle of the plane R

. Locally, the topology of the unit cylinder and of the

Möbius band and of R

are the same. Globally they are all different. (The

neighborhoods at the left and right edge of the rectangle are independent while on

the unit cylinder they are connected.) Another example is the ordinary sphere S

embedded in the R

. Although its topology is locally the same as that of R

globally it is different from any part of the R

. (From the stereographic projection

which is a continuous one-one mapping it is known that the global topology of the

sphere S

is the same as that of the completed or better compactiﬁed plane R

with

the ‘inﬁnite point’ and its neighborhoods added.) The S

-problem was maybe ﬁrst

considered by Merkator (1512–1569) as the problem to project the surface of the

earth onto planar charts. The key to describe manifolds are atlases of charts.

Topological space is a vast category, topological product is a construction of

new topological spaces from simpler ones. Manifold is yet another construction to

a similar goal. An m-dimensional manifold is a topological space the local

topology of which is the same as that of R

. Not every topological space is a

manifold. Since a manifold is a topological space, a topological product of man-

ifolds is just a special case of topological product of spaces. A simple example is

the two-dimensional torus T

¼ S

 S

of Fig. 1.3.

More special cases of topological spaces with richer structure are obtained by

assigning to them additional algebraic and analytic structures. Algebraically, the

Fig. 1.3 The two-

dimensional torus

¼ S

 S

(b)(a)

Fig. 1.2 a The unit cylinder

and b the Möbius band

1 Introduction 3

is usually considered as a vector space (see Compendium at the end of this

book) over the scalar ﬁeld of real numbers, that is, a linear space. It may be

attached with the usual topology which is such that multiplication of vectors by

scalars, ðk; xÞ7!k x, and addition of vectors, ðx; yÞ7!x þ y, are continuous

functions from R R

to R

and from R

 R

to R

, respectively. As was

already mentioned, this topology can likewise be derived as a product topology

from n factors R or from the Euclidean metric related to the usual Euclidean scalar

product of vectors. The latter deﬁnes lengths and angles. For good reasons a metric

will be used only on a much later stage as it is too restrictive for many consid-

erations. So far, linear operations are deﬁned and continuous, for instance

linear dependence is deﬁned, but angles and orthogonality remain undeﬁned. If

; i ¼ 1...n are n linearly independent vectors of R

, then any vector x 2 R

can

be written as x ¼

with uniquely deﬁned components x

in the basis fe

If X and Y are two topological vector spaces, then their algebraic direct sum

Z ¼ X  Y with the product topology is again a topological vector space. Any

vector z 2 Z is uniquely decomposed into z ¼ x þy, x 2 X, y 2 Y, and the

canonical projections pr

and pr

, pr

ðzÞ¼x, pr

ðzÞ¼y are continuous.

(Orthogonality of x and y again is not an issue here.)

Analysis is readily introduced in topological vector spaces. Let f : R

! R

any function, f ðxÞ¼y or more explicitly with respect to bases, f ðx

; ...; x

Þ¼

ðy

; ...; y

Þ, that is, f

ðxÞ¼y

. If the limits



¼ lim

t!0

ðx þ te

Þf

ðxÞ

ð1:1Þ

exist and are continuous in x, then the vector function f is differentiable with

derivative

; ...;



: ð1:2Þ

For n ¼ 1 think of a velocity vector as the derivative of xðtÞ, for m ¼ n ¼ 4 think

of the electromagnetic ﬁeld tensor as twice the antisymmetric part of the derivative

of the four-potential A

ðx

Þ. Higher derivatives are likewise obtained.

Manifolds are in general not vector spaces (cf. Figs. 1.2, 1.3) and therefore

derivatives of mappings between manifolds cannot be deﬁned in a direct way.

However, if m-dimensional manifolds are sufﬁciently smooth, one may at any

given point of the manifold attach a tangent vector space to it and project in a

certain way a neighborhood of that point from the manifold into this tangent space.

Then one considers derivatives in those tangent spaces. If a point moves in time on

a manifold, its velocity is a vector in the tangent space. If space–time is a curved

manifold, the electromagnetic four-potential is a vector and the ﬁeld a tensor in the

tangent space.

The derivative of a vector ﬁeld meets however a new difﬁculty: the numerator

of Eq. 1.1 is the difference of vectors at different points of the manifold which lie

4 1 Introduction

in different tangent spaces. Such differences cannot be considered before the

introduction of afﬁne connections between tangent spaces in Chap. 7. However,

there are two types of derivative which may be introduced more directly and which

are considered in Chap. 4: Lie derivatives and exterior derivatives. They yield also

the basis for the study of Pfaff systems of differential forms playing a key role for

instance in Hamilton mechanics and in thermodynamics. In any case, analysis

leads to an important new construct of a manifold with a tangent space attached to

each of its points, the tangent bundle.

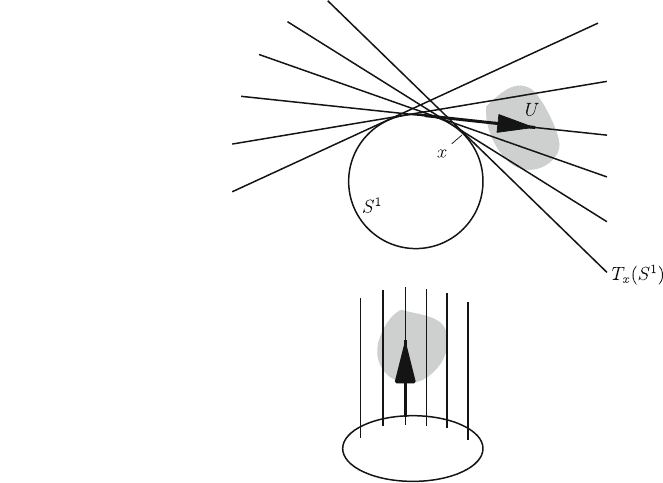
As an example, the circle S

as a one-dimensional manifold is shown in the

upper part of Fig. 1.4 together with its tangent spaces T

ðS

Þ at points x of S

.All

those tangent spaces together with the base manifold S

form again a manifold: If

all tangent spaces are turned around by 90



as in the lower part of Fig. 1.4,a

neighborhood of the tangent vector indicated in the upper part is obviously

smoothly deformed only. Hence it is natural to introduce a topology in the whole

construct which is locally equivalent to the product topology of V  R where V is

an open set of S

and hence in the whole this topology is equivalent to that of an

inﬁnite cylinder, the vertically inﬁnitely extended version of Fig. 1.2a. (Note that

the tangent vector spaces to different points of a manifold are considered disjoint

by deﬁnition. In the upper panel of Fig. 1.4 the lines in clockwise direction from S

must therefore be considered on a sheet of paper different from that for the lines in

counterclockwise direction in order to avoid common points.) In this topology, the

canonical projection p from the tangent spaces to their base points in S

Fig. 1.4 The circle S

attached with a bundle of

one-dimensional tangent

spaces T

ðS

Þ (upper part). A

neighborhood U of a tangent

vector marked by an arrow is

indicated. If the tangent

spaces are turned around as

shown in the lower part, the

neighborhood U is just

smoothly deformed

1 Introduction 5

continuous. Such a rather special construct of a manifold is called a bundle, in the

considered case a tangent bundle TðS

Þ which is a special case of a vector bundle.

All tangent spaces to a manifold are isomorphic to each other, they are iso-

morphic to R

if the manifold M has a given (constant) dimension m (its local

topology is that of R

). Such a bundle of isomorphic structures is in general called

a ﬁber bundle, in the considered case the tangent bundle TðMÞ with base M and

typical ﬁber R

(tangent space). Fiber bundles are somehow manifolds obtained

by gluings along ﬁbers. The complete deﬁnition of bundles given in Chap. 7

includes additionally transformation groups of ﬁbers. The characteristic ﬁber of a

ﬁber bundle need not be a vector space, it can again be a manifold. As already

stated, a ﬁber bundle is again a new special type of manifold. Hence, one may

construct ﬁber bundles with other ﬁber bundles as base...

Given tangent and cotangent spaces in every point of a manifold, the latter as

the duals to tangent spaces, a tensor algebra may be introduced on each of those

dual pairs of spaces. This leads to the concept of tensor ﬁelds and the corre-

sponding tensor analysis. Totally antisymmetric tensors are called forms and play

a particularly important role because E. Cartan’s exterior calculus and the inte-

gration of forms leading to de Rham’s cohomology provide the basis for the

deepest interrelations between topology, analysis and algebra. In particular ﬁeld

theories like Maxwell’s theory are most elegantly cast into cases of exterior cal-

culus. Tensor ﬁelds and forms as well as their Lie derivatives along a vector ﬁeld

and the exterior derivative of forms are treated in Chap. 4. Besides the tensor

notation related to coordinates which is familiar in physics, the modern coordinate

invariant notation is introduced which is more ﬂexible in generalizations to

manifolds, in particular in the exterior calculus.

On the real line R, differentiation and integration are in a certain sense inverse

to each other due to the Fundamental Theorem of Calculus

ðyÞdy ¼ f ðxÞf ðaÞ: ð1:3Þ

In general, however, while differentiation needs only an afﬁne structure, integra-

tion needs the deﬁnition of a measure. However, it turns out that the integration of

an exterior differential n-form on an n-dimensional manifold is independent of the

actual local coordinates of charts. It is treated in Chap. 5. This implies the classical

integral theorems of vector analysis and is the basis of de Rham’s cohomology

theory which connects local and global properties of manifolds.

There are two classical roots of modern algebraic topology and homology,

of which two textbooks which have many times been reprinted still maintain

actuality not only for historical reasons. These are that of Herbert Seifert and

William Threlfall, Dresden [1], and that of Pawel Alexandroff and Heinz Hopf,

Göttingen/Moscow [2]. Seifert was the person who coined the name ﬁber

space, then in a meaning slightly different from what is called ﬁber bundle

nowadays.

6 1 Introduction