Eschrig H. Topology and Geometry for Physics

Подождите немного. Документ загружается.

5.3 Integration of Differential Forms

First, a regular domain X in a paracompact smooth orientable n-dimensional

manifold M is deﬁned: every point x 2 M is either an inner point of X or an inner

point of M n X or there is a coordinate neighborhood ðU; uÞ of x such that uðU \

XÞ¼uðUÞ\R



where R



is the half-space of points x ¼ðk

; ...; k

Þ2R

with

1: In other words, the boundary of X is locally diffeomorphic to an ðn 1Þ-

dimensional hyperplane (the hyperplane

¼ 1 of R

). In this precise sense a

regular domain X is a domain with smooth boundary oX: Note, however, that a

regular domain X need not have a boundary at all, it could for instance be all M:

Let X have a boundary. Consider a smooth real function F on a neighborhood

of oX, which is constant on oX and for which Fðx

Þ\Fðx

Þ whenever x

is an inner

point of X and x

is an inner point of M n X: Let x 2 oX: A vector X of the

n-dimensional tangent space T

ðMÞ is an outer vector to X,ifXF [ 0: Consider

now the ðn 1Þ-dimensional tangent space T

ðoXÞ at a boundary point x 2 oX:

A base X

; ...; X

n1

in this tangent space is called coherently oriented with M,if

with an outer vector X to X the base X; X

; ...; X

n1

of T

ðMÞ deﬁnes the orien-

tation of M, that is, the dual base dx; dx

; ...; dx

n1

in T



ðMÞ deﬁnes the positive n-

form dx ^ dx

^^dx

n1

: It is clear that this deﬁnition of coherent orientation

does not depend on the chosen outer vector X, and that there is a coordinate

neighborhood U of x in oX and there are local coordinates x

; ...; x

n1

in U

smoothly deﬁning an orientation coherent with that of M: In other words, an

orientation of T

ðoXÞ coherent with that of M is a smooth and hence all the more

continuous function of x on oX: Since an orientation can only have two discrete

values, if the orientation on oX is coherent with that of M, it must be constant on

each topological component of oX:

Now, let X be a regular domain in M and let x be an at least continuous n-form,

n ¼ dim M, with compact support. In order to deﬁne the integral of x over X,

regular n-simplices are deﬁned as diffeomorphisms r from a neighborhood in R

of the standard n-simplex D

into M: If r preserves orientation, it is called an

oriented regular simplex.

A partition of unity on M (which exists since M is paracompact) is used to

reduce the integral over X to a sum of integrals over oriented regular simplices

covering supp x \ X: Since supp x \ X is compact, it has a ﬁnite open cover

; ...; U

g: Let furthermore U be the open set U ¼ M nðsupp x \ XÞ, so that

fU; U

; ...; U

g is a ﬁnite open cover of M: Consider a partition of unity

f/; /

; ...; /

g subordinate to this open cover of M, that is, supp / 

U; supp /

 U

; i ¼ 1; ...; m and /ðxÞþ

ðxÞ¼1 on M: If U

 X, choose

an oriented regular simplex r

the image of D

of which contains U

and is entirely

in X (which is always possible since X is closed and U

is open). If U

\ oX is non-

empty, choose an oriented regular n-simplex r

with X  r

ðD

ÞU

\ X and so

that oX intersects only with the image of the face of D

opposite to the origin

(Fig. 5.4).

5.3 Integration of Differential Forms 127

Although U may intersect X, no simplex need be chosen for U since supp / \

supp x \ X ¼ £ and hence /ðxÞxðxÞ¼0 on X: The images of the simplices

; i ¼ 1: ...; m form a closed (overlapping) cover of supp x \ X, and r

ðD

Þ\

ðM n XÞ¼£ for all i: On the other hand, /

ðxÞxðxÞ are smooth n-forms with

support in U

,ifx is smooth (since the /

are smooth by deﬁnition of a partition of

unity), and x ¼ /x þ

x on M: Since, however, /x ¼ 0 on X; x ¼

on X: Therefore, one may deﬁne

x ¼

i¼1

x ¼

i¼1



ð/

xÞ: ð5:30Þ

The last sum is over well deﬁned ordinary integrals in R

: It remains to show that

this expression is unique in the sense that it does not depend on the used partition

of unity.

Indeed, consider another partition fw; w

; ...; w

g subordinate to the open cover

fU; V

; ...; V

g and correspondingly chosen simplices r

; i ¼ 1; ...; l: (U was

deﬁned by X and x only, hence it is not changed.) On supp x \ X, there holds

/ ¼ w ¼ 0: Hence,

i¼1

x ¼

j¼1

x ¼

By the above construction, for each pair ði; jÞ one has that suppðw

xÞ\r

ðD

Þ¼

suppð/

xÞ\r

ðD

Þ: It may be empty. If it is non-empty, r

1

 r

is an ori-

entation preserving diffeomorphism on its open domain of deﬁnition in R

(open

neighborhood of part of D

) which maps part of D

into D

: Therefore,

x ¼



ðw

xÞ¼

ðr

1

 r



ðr



ðw

xÞÞ

0

ð/

xÞ¼

Fig. 5.4 Regular 2-simplices

for a parition of unity of M

128 5 Integration, Homology and Cohomology

and both double sums in the previous expressions are equal. (ðr

1

 r



 r



 r

1



 r



¼ r

0

was used, see p. 74).

The deﬁnition (5.30) may now justly be considered to be the integral of the n-

form x over the regular domain X in M: If, on the other hand, x is a smooth

ðn  1Þ-form on M; dim M ¼ n, and x has compact support, then dx has also

compact support, and Stokes’ theorem holds:

dx ¼

x: ð5:31Þ

Proof Use the partition of unity as in the deﬁnition of

: Since

¼ 1 on a

neighborhood of supp x \ X;

¼ d

¼ 0 there and hence

dð/

xÞ¼

dx ¼ dx on X: For U

 X;

x ¼ 0 because /

¼ 0 on oX. /

¼ 0 on

the image of dr

too, and since a regular simplex is all the more a smooth singular

simplex, (5.29) applies, and

x ¼

x ¼ 0: Let U

\ oX 6¼ £: Then,

6¼ 0 in the interior of r

ðD

n1

Þ only where D

n1

is the face of D

opposite to

the origin. Since D

n1

is coherently oriented with D

and r

is orientation pre-

serving, r

ðD

n1

Þ is coherently oriented with r

ðD

Þ: Again (5.29) applies,

and

dð/

xÞ¼

dð/

xÞ¼

x ¼

x: Hence in total,

dx ¼

dð/

xÞ¼

x ¼

x: h

Observe for both the deﬁnition of the integral over X and the proof of Stokes’

theorem: If X itself is compact, then x need not have compact support in M:

5.4 De Rham Cohomology

Consider as an example dim M ¼ 2 and the equation dx ¼ q where a 2-form q is

given and a 1-form x, in local coordinates x ¼ x

þ x

; is sought. One has

dx ¼ðox

=ox

 ox

=ox

Þdx

^ dx

: How must q behave in order that the

equation has a solution x? For any domain X of ﬁnite measure one has

q ¼

dx ¼

x: Hence, if X has no boundary (for instance if X ¼ S

is the two-

dimensional sphere), then

q ¼ 0 must hold as a necessary condition for a

solution x to exist. If M ¼ R

; then there are no such compact domains X without

boundary, and no such condition need be posed on q:

In the latter case, R

may be considered as the complex plane, x

Re z; x

¼ Im z, and x may be considered as a complex function,

x ¼ iðx

Þ: For an analytic function

x; in this notation dx ¼ 0 by the Cauchy–Riemann

equations, and hence

x ¼ 0; if X is an oriented domain of analyticity of

x the

oriented boundary of which is oX: This integral is in the adopted notation the

imaginary part of the complex integral, and its vanishing is part of Cauchy’s

5.3 Integration of Differential Forms 129

integral theorem. For the integral to vanish it is sufﬁcient that oX is the complete

oriented boundary of a domain of analyticity of

The two natural questions that arise in these considerations are: (i) which are

the domains X of a manifold M that have no boundary, and (ii) which surfaces of

M are complete oriented boundaries of oriented domains X: If for instance M is the

two-dimensional torus of Fig. 1.3 on p. 3 (which is orientable), then non of the

circles drawn in the ﬁgure is a complete oriented boundary, because as a boundary

it would have to have both orientations simultaneously. Only pairs of oppositely

oriented circles (winding around the torus in opposite directions are boundaries of

domains of the torus.

A domain which has no boundaries is called a cycle. (For instance a circle is a

one-dimensional cycle, an n-dimensional sphere S

is an n-cycle.) Clearly, every

boundary is a cycle, but, as the above example shows, the reverse need not be true.

Not every cycle need be a boundary. The classiﬁcation of cycles and boundaries of

manifolds is the subject of homology theory. However, this theory turned out to be

simpler in a more general setting.

In Sect. 5.2, as a certain generalization of domains of manifolds r-chains of

singular r-simplices were introduced. Consider the real vector space

ðM; RÞ of

r-chains c ¼

of linear combinations with real coefﬁcients k

of smooth

singular r-simplices r

: Only the smooth case is treated in the sequel although most

results hold also true in the continuous case. Therefore, the presubscript will be

omitted, C

ðM; RÞ¼

ðM; RÞ: Let B

ðM; RÞ be the set of boundaries and

ðM; RÞ the set of cycles of C

ðM; RÞ: Since linear combinations of boundaries

are boundaries and linear combinations of cycles are cycles, both sets are linear

subspaces of C

ðM; RÞ: The boundary operator (recall that its operation on

ðM; KÞ is sometimes denoted by o

) maps C

ðM; RÞ into B

r1

ðM; RÞ

r1

ðM; RÞC

r1

ðM; RÞ (since o o ¼ 0), and by deﬁnition of cycles it maps

ðM; RÞ to 0:

Im o

¼ B

r1

ðM; RÞ; Ker o

r1

¼ Z

r1

ðM; RÞB

r1

ðM; RÞ; ð5:32Þ

where Im o

means the image of the boundary operator o

deﬁned on C

ðM; RÞ;

and the kernel Ker o

r1

is deﬁned as the preimage of the origin of C

r2

ðM; RÞ in

r1

ðM; RÞ: (See Compendium C.1 on homomorphisms.)

The direct sum of all C

ðM; RÞ; r 2 Z may be considered as a graded (by r)

vector space CðM; RÞ with an endomorphism o of degree 1:

CðM; RÞ¼f!

rþ1

ðM; RÞ!

r1

ðM; RÞ!

g: ð5:33Þ

CðM; RÞ is called a (real) chain complex. Recall that by deﬁnition C

ðM; KÞ¼

f0g for r\0, hence CðM; KÞ may be considered as an inﬁnite sequence of map-

pings o

of modules. Together with a collection of r-simplices (repetition allowed)

the chain complex CðM; ZÞ contains all their oriented faces as ðr  1Þ-simplices,

the oriented faces of the latter as ðr  2Þ-simplices and so on down to the oriented

edges of 2-simplices as line elements and their oriented endpoints as 0-simplices

130 5 Integration, Homology and Cohomology

(set of all vertices of the original collection). This is how complexes originally

were introduced in topology. In the case of CðM; RÞ all those collections have in

addition real coefﬁcients.

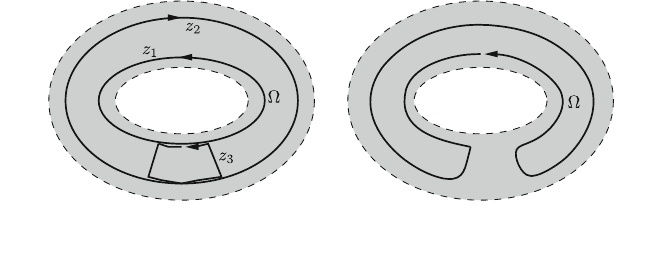
As an example, consider the three 1-cycles on the 2-torus depicted on the left

part of Fig. 5.5. As was already discussed, the cycles z

and z

are not boundaries.

Depending on the orientation of the torus, b ¼ z

þ z

is the boundary of the

visible domain X on the torus or of X: Let the ﬁrst case be valid. Then, z

is the

boundary of minus the visible domain enclosed by this cycle. The sum b ¼

þ z

depicted on the right part of the ﬁgure is the boundary of the visible

enclosed domain denoted again X on this ﬁgure. One realizes, if certain cycles are

not boundaries, nevertheless their sums or differences may be boundaries. The

alert reader also immediately realizes the relevance of considerations of that type

for complex analysis, and indeed complex analysis of several variables was one of

the early motivations to develop homology theory.

Two r-cycles z

; z

are called homologous, z

z

, if their difference is an

r-boundary:

ðM; KÞ3z

z

() z

 z

2 B

ðM; KÞ: ð5:34Þ

A boundary is called homologically trivial. Hence, two cycles are homologous, if

their difference is homologically trivial. Clearly, the homology relation (5.34)is

an equivalence relation. The Abelian group of equivalence classes in homology of

r-cycles is called the rth homology group H

ðM; KÞ: It is the quotient group

ðM; KÞ¼Z

ðM; KÞ=B

ðM; KÞ¼Ker o

=Im o

rþ1

: ð5:35Þ

In the case K ¼ Z; as every Abelian group it may also be considered a module; if

K is a ﬁeld (like R), more speciﬁcally it is a vector space. Unlike Z

ðM; KÞ and

ðM; KÞ; H

ðM; KÞ is ﬁnite-dimensional in most interesting cases.

The reader may convince himself from the above example that the main

topological difference between the 2-torus T

and the plane R

is that in R

every

cycle is a boundary (of the encircled domain) while in T

there are cycles which

are not boundaries. If all cycles of a chain complex (5.33) are boundaries, this

Fig. 5.5 1-cycles on a 2-torus. Left: z

and z

are not boundaries, z

is a boundary. Right:

b ¼ z

þ z

is a boundary

5.4 De Rham Cohomology 131

means that Im o

rþ1

¼ Ker o

for all r, or, equivalently, that all homology groups

are trivial: H

ðM; KÞ¼f0g: A sequence of morphisms between algebraic objects

like (5.33) is called an exact sequence, if the image of one morphism in the

sequence is the kernel of the next. Sequences of non-trivial chain complexes are

not exact.

Yet, exact sequences form a powerful tool in algebra. For instance, the exact

sequence of homomorphisms of Abelian groups or modules (in particular vector

spaces)

0 ! G!

means that f is injective: Since the image of the ﬁrst mapping can only consist of

the zero element of G, the kernel of f must be f0g, and by linearity f must be

injective. If, on the other hand, the sequence

G!

H ! 0

is exact, this means that f is surjective: since all of H is mapped to 0 by the right

mapping, its kernel is all of H which also must be the image of f : Hence, the exact

sequence

0 ! G!

H ! 0

means that the homomorphism f is indeed an isomorphism. Interpret as an exercise

the so called short exact sequence for the case of Abelian groups or modules,

0 ! H ! G ! G=H ! 0;

where H is a subgroup or submodule of G and G=H is the quotient structure.

Coming back to the homology groups H

ðM; KÞ of (5.35), it will be seen later

that their dimensions are topological invariants.

ðMÞ¼dim H

ðM; RÞð5:36Þ

is called the rth Betti number of M:

Recall that a 0-simplex is just a point of M, a 0-chain hence is a linear com-

bination of points. Since C

1

ðM; RÞ is trivial, a 0-chain has zero boundary. Hence,

every 0-chain is a 0-cycle. The standard 1-simplex is a line element, its image in M

is a ﬁnite path between two points. Every pair of points ðz

; z

Þ which can be

connected by a path X in M yields a boundary as its difference: oX ¼ z

 z

Hence, all points which can be connected by a path in M are homologous: the

pathwise connected components of M form a base of the vector space H

ðM; RÞ;

and the zeroth Betti number of any manifold M is equal to the number of pathwise

connected components of M:

If M is contractible (see Sect. 2.5), that is M may continuously be contracted

into one point, then it is intuitively clear and will formally be proved in the next

132 5 Integration, Homology and Cohomology

section that every r-cycle, r [ 0 is a boundary, that is, H

ðM; RÞ¼f0g: Hence,

ðMÞ¼0; r [ 0, if M is contractible. In particular,

ðR

Þ¼1; b

ðR

Þ¼0; r [ 0; n 1: ð5:37Þ

Less trivial cases will be considered in the sequel.

Comparison of o  o ¼ 0 with d  d ¼ 0 for the exterior derivation d of degree

+1 and consideration of Stokes’ theorem suggest a duality between the chain

complex CðM; RÞ and the graded algebra DðMÞ of exterior forms:

DðMÞ¼f 

rþ1

ðMÞ 

r1

ðMÞ 

g: ð5:38Þ

Again, as previously in Sect. 4.2, D

¼f0g if r\0 or r [ dim M: An exterior

r-form x on M is called a closed form,ifdx ¼ 0, it is called an exact form,if

there exists an ðr  1Þ-form r so that x ¼ dr: Two closed forms x

and

; dx

¼ 0 are called cohomologous to each other, x

x

, if their difference is

exact, that is, x

 x

¼ dr for some form r: An exact form is called cohomo-

logically trivial. Clearly, every exact form is closed, and clearly, closed forms as

well as exact forms form linear subspaces of the vector spaces D

ðMÞ: De Rham’s

cohomology group is the quotient group

ðMÞ¼fclosed r-formsg=fexact r-formsg¼Ker d

=Im d

r1

: ð5:39Þ

Since dim H

ðMÞdim D

ðMÞ because H

ðMÞ is a quotient space of a subspace

of D

ðMÞ; clearly dim H

ðMÞ¼0 for r\0 or r [ dim M: Moreover, from

dim D

1

¼ 0 it follows that Im d

1

¼f0g, and hence H

ðMÞ¼Ker d

: Now, a

0-form x

is a real function on M, and hence dx

¼ 0 means that the function x

is constant on each pathwise connected component of M (by integration of dx

along any path in M). If M has m components, then Ker d

is the space of real

m-tuples which means that dim H

ðMÞ¼dim Ker d

is equal to the number of

pathwise connected components of M and hence equal to the Betti number b

ðMÞ:

It will be seen that this is not an accident.

Let x be a closed r-from and let z be an r-cycle. Consider the real number

hx; zi¼

given by the integral (5.27, 5.28). It is obviously bilinear in x and z as suggested

by the way of writing. Let x

¼ dr be any exact r-form and let b ¼ oz

be any

r-boundary. Then, by virtue of Stokes’ theorem (5.29) for singular chains,

hx þ x

; zi¼

x þ

dr ¼

x þ

r ¼hx; zi;

since oz ¼ 0 for a cycle z: Likewise,

5.4 De Rham Cohomology 133

hx; z þbi¼

x þ

x ¼

x þ

dx ¼hx; zi;

since dx ¼ 0 for a closed form x: In effect, the considered integral depends on the

homology class ½z of the cycle z and on the cohomology class ½x of the closed

form x only:

h½x; ½zi ¼

x ð5:40Þ

is a linear form on the space H

ðM; RÞ; that is, an element of the dual space

ðH

ðM; RÞÞ



; and every element ½x of H

ðMÞ yields uniquely such a linear form.

In other words, (5.40) yields a homomorphism of vector spaces

ðMÞ!ðH

ðM; RÞÞ



: ð5:41Þ

This reﬂects the point of view of letting ½x run through H

ðMÞ and considering

(5.40) as linear functions on H

ðM; RÞ; that is, as elements of ðH

ðM; RÞÞ



De Rham’s theorem states that (5.41) is in fact an isomorphism.

In this connection the real number (5.40) is called the period of the r-form x

over the cycle z,

perðzÞ¼h½x; ½zi ¼

x: ð5:42Þ

De Rham’s theorem implies that, if there exists a linear function per on Z

ðM; RÞ

with the property perðbÞ¼0 for every boundary b, then there exists a closed

r-form x so that

x ¼ perðzÞ: It also implies

dim H

ðMÞ¼dimðH

ðM; RÞÞ



¼ dim H

ðM; RÞ¼b

ðMÞ: ð5:43Þ

Two isomorphic vector spaces have the same dimension, and two spaces con-

nected by a non-degenerate bilinear form have also the same dimension. More-

over, H

ðMÞH

ðM; RÞ; if b

ðMÞ\1, since two real finite-dimensional vector

spaces of the same dimension are isomorphic. Now, considering (5.40)asa

bilinear form on H

ðMÞH

ðM; RÞ; for every ½x 6¼ 0 there is a ½z so that (5.40)

is non-zero. Otherwise (5.40) would yield the same result on all ½z for ½x 6¼ 0 and

for ½x

¼0 and (5.41) could not be an isomorphism. Likewise, for every ½z 6¼ 0

there is an ½x so that (5.40) is non-zero. Otherwise for all ½x2dim H

ðMÞ

(5.40) would yield the same value 0 on ½z 6¼ 0 and on ½z

¼0 and (5.41) would

not be surjective.

An immediate consequence is

ðMÞ¼0 for r [ dim M ð5:44Þ

134 5 Integration, Homology and Cohomology

and also that dim H

ðMÞ¼0 for all r [ 0, if M is contractible. Hence in par-

ticular, on a contractible manifold M the necessary and sufﬁcient condition for the

equation dx ¼ q to have a solution x is that q is closed, dq ¼ 0, since

dim H

ðMÞ¼0 means that every closed form is exact.

In these considerations both H

ðMÞ and H

ðM; RÞ are treated as real vector

spaces. (Recall that every vector space is an Abelian group with respect to vector

addition. This justiﬁes to retain the names homology group and cohomology group

in the considered more special cases.) However, DðMÞ is also an algebra with

respect to exterior multiplication. It is easily seen that the wedge product is

compatible with the cohomology classes of DðMÞ: Indeed, let m; m

; x; x

be closed

forms and let m m

¼ dq; x x

¼ dr for some forms q and r, that is, ½m m

¼

0; ½x x

¼0: Then, obviously m ^ x and m

^ x

are also closed forms, and

m ^ x m

^ x

¼ðm m

Þ^x þ m

^ðx x

Þ¼dq ^ x þm

^ dr

¼ dðq ^ x þð1Þ

^ rÞþð1Þ

q ^ dx ð1Þ

^ r:

The last two terms vanish since x and m

are closed forms. Hence, m ^x  m

^ x

is an exact form. This implies that m ^ðx x

Þ and ðm  m

Þ^x as special cases

of the just considered one are also exact forms. This altogether means that the

cohomology class ½m ^ x does not depend on the representatives of the coho-

mology classes ½m and ½x, and one may deﬁne a wedge product in H

ðMÞ by

½m^½x¼½m ^ x: ð5:45Þ

Therefore, the de Rham cohomology H

ðMÞ; the direct sum of all H

ðMÞ; is

indeed again a graded algebra.

5.5 Homology and Homotopy

The alert reader may anticipate from the last section that there is a close con-

nection between the homology of chain complexes and homotopy.

Let F : M ! N be a (smooth) mapping from the (smooth) manifold M into the

(smooth) manifold N: (Recall that generally smooth entities are considered in this

volume.) Let CðM; RÞ be the chain complex on M: A (smooth) singular r-simplex

r 2 CðM; RÞ is a mapping of a neighborhood of the standard r-simplex in R

into

M: Clearly, F



ðrÞ¼F  r is a singular r-simplex in N: Since the oriented

boundary of r was deﬁned in (5.25) as the push forward by r of the oriented

boundary of the standard r-simplex, it is clear that F



maps cycles on M into cycles

on N and boundaries on M into boundaries on N: These mappings need of course

not be one–one, also, M and N need not have the same dimension. Recall that a

singular r-simplex in N even may consist of a single point. Nevertheless, and that

is one of the main advantages of singular chains, it is clear that F



 o ¼ o F



and that F



: H

ðM; RÞ!H

ðN; RÞ is a homomorphism of vector spaces. Indeed,

5.4 De Rham Cohomology 135

if z

z

are homologous chains of CðM; RÞ then F



ðz

ÞF



ðz

Þ are homologous

chains of CðN; RÞ:

Now, let F

and F

be two homotopic mappings from M into N, that is

(Sect. 2.5), there is a continuous mapping H : ½0; 1M ! N with Hð0; Þ ¼ F

and Hð1; Þ ¼ F

. H may be extended to

I  M where

I is an open neighborhood in

R of the closed interval ½0; 1: Together with M;

I  M is also a smooth manifold.

Hence, H may be assumed to be smooth since F

and F

are smooth and a

continuous function on a smooth manifold (which latter is locally diffeomorphic

with R

) may be arbitrarily closely approximated by a smooth function.

Let z 2 CðM; RÞ be an r-cycle. Then, ðId

; zÞ2Cð

I  M; RÞ is a singular

ðr þ 1Þ-chain, which is the image of an ðr þ 1Þ-cylinder in R

nþ1

of height 1 whose

basis and top is the same cycle of ordinary simplices. Clearly its boundary is

ð1; zÞð0; zÞ (Fig. 5.6, z itself as a cycle has no boundary). Hence, H



ðId

; zÞ2

CðN; RÞ is also a chain whose boundary is ðF



ðzÞðF



ðzÞ: Since the latter

difference is a boundary, ðF



ðzÞðF



ðzÞ are homologous:

The homomorphisms in homology ðF



and ðF



of homotopic maps F

and

from M into N are the same: ðF



¼ðF



Finally, let M and N be homotopy equivalent, that is, there exist mappings

F : M ! N and G : N ! M so that G  F ﬃ Id

and F  G ﬃ Id

(Sect. 2.5).

Since ðId



: H

ðM; RÞ!H

ðM; RÞ is the identity homomorphism and

ðG  FÞ



¼ G



 F



(cf. p. 73), it follows that G



¼ðF



1

and hence H

ðM; RÞ

and H

ðN; RÞ are isomorphic:

Homotopy equivalent manifolds have isomorphic homology groups.

Consider now a contractible manifold, that is, a manifold that is homotopy

equivalent to the one-point manifold fxg: In the latter manifold, every singular r-

simplex is a constant mapping r

of the standard r-simplex to x: Hence, every r-

chain is given as kr

; k 2 R; r 0: From (5.25) it follows that for r [ 0 the

boundary of kr

is kr

r1

if r is even and is the zero r-chain, if r is odd. That means

that for r [0; r odd, every r-chain is a cycle and at the same time is a boundary of

an ðr þ 1Þ-chain, while for r [ 0; r even, there are no non-zero cycles. In sum-

mary, all homology groups H

ðfxg; RÞ for r [ 0 are trivial (consist of the zero

element only and hence are also zero-dimensional). In view of the last theorem the

same is true for any contractible manifold, which also proves (5.37).

Fig. 5.6 A cylinder of height

1 with a cycle z (boundary of

a triangle) as basis

136 5 Integration, Homology and Cohomology