Ellis,J. Pressure transients in water engineering, A guide to analysis and interpretation of behaviour

Подождите немного. Документ загружается.

ﬂow has the consequence of producing reversed pump rotation as

illustrated in Fig. 21.19.

A stiffer valve sleeve is required to avoid inversion. Increasing the

maximum allowable differential head to in excess of þ80 m to say

100 m produces the desired effect. Figure 21.20 shows velocity changes

at the valve and at chainage 500 m. An oscillation in velocity was

predicted to develop following sleeve closure after about 4.7 s, with

432

Head (mAD)

Time

(

)

Series 1

Series 2

Series 3

Series 4

Red valve – longer system: c

= 0.08, h

max

= 60.0

–10

–20

0.005

0.475

0.946

1.416

1.886

2.357

2.027

3.218

3.768

4.218

4.749

5.109

5.650

6.120

6.590

7.061

7.581

8.002

8.472

8.942

9.413

9.883

10.354

10.824

11.294

11.765

12.285

12.706

13.176

13.646

14.117

14.587

Fig. 21.18. Head at failing sleeve valve after pump trip

Pump speed/design speed

Time (s)

Series 1

Red valve – longer system: c

= 0.08, h

max

= 60.0

0.005

0.480

0.955

1.431

1.906

2.381

2.857

3.332

3.807

4.283

4.758

5.233

5.708

6.184

6.659

7.134

7.610

8.085

8.560

9.036

9.511

9.986

10.461

10.937

11.412

11.887

12.363

12.838

13.313

13.789

14.264

1.2

1.0

0.8

0.6

0.4

0.2

0.0

–0.2

–0.4

–0.6

–0.8

–1.0

Fig. 21.19. Pump speed for sleeve valve failure

Pressure transients in water engineering

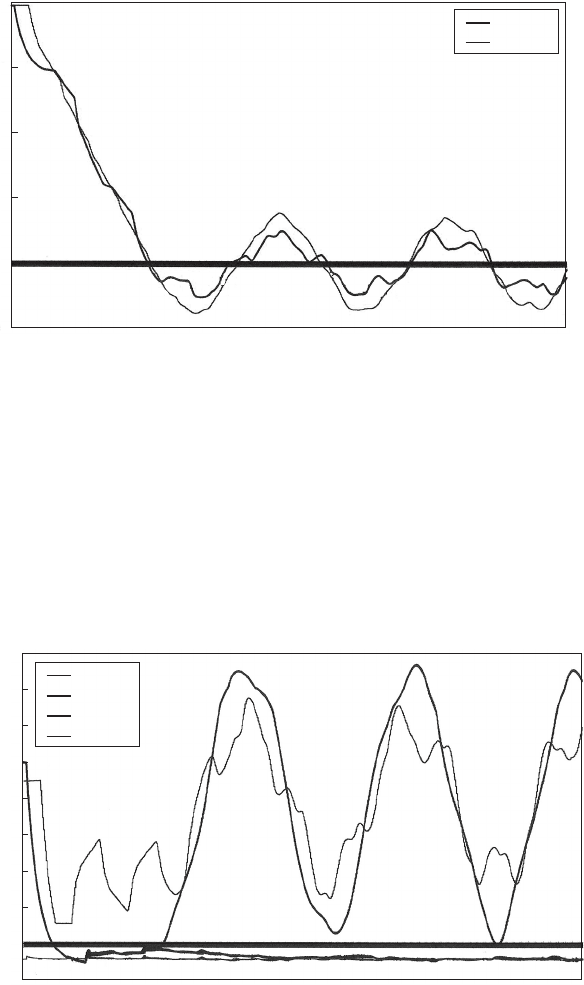
this oscillation taking place around the zero ﬂow condition. A similar

velocity variation occurs at the valve inlet and with no continuous

reversed ﬂow there is no motivation for reversed pump rotation to

occur. The predicted oscillation was due to substantial deformation of

the sleeve. Under the action of transient effects within the pipeline,

only a 10 litre margin remains before inversion could occur. Head

changes are shown in Fig. 21.21, with peak head of þ75 m at the

433

Velocity (m/s)

Time (s)

Series 1

Series 2

Red valve – longer system: c

= 0.08, h

max

= 100.0

0.005

0.603

1.200

1.798

2.396

2.994

3.592

4.189

4.787

5.385

5.983

6.581

7.178

7.776

8.374

8.972

9.570

10.167

10.765

11.363

11.961

12.559

13.156

13.754

14.352

14.950

15.548

16.145

16.743

17.341

17.939

18.537

1.5

0.5

–0.5

Fig. 21.20. Velocity variation at sleeve valve in longer pipeline

Head (mAD)

Time (s)

Series 1

Series 2

Series 3

Series 4

Red valve – longer system: c

= 0.08, h

max

= 100.0

0.005

0.612

1.220

1.818

2.430

3.043

3.650

4.258

4.866

5.473

6.081

6.688

7.296

7.904

8.511

9.119

9.726

10.334

10.942

11.549

12.157

12.764

13.372

13.080

14.587

15.195

15.802

16.410

17.018

17.625

18.233

18.840

–10

Fig. 21.21. Head variations at sleeve valve in longer pipeline

Check valve characteristics

valve outlet. A large oscillation was predicted following deceleration of

the reversed velocity.

It should be noted that use of a sleeve which allows inversion to occur

may produce lower system pressures generally than when a stiffer sleeve

is used which prevents inversion. However, the inverted sleeve is liable

to suffer damage and there is the matter of inverse pump rotation to

consider.

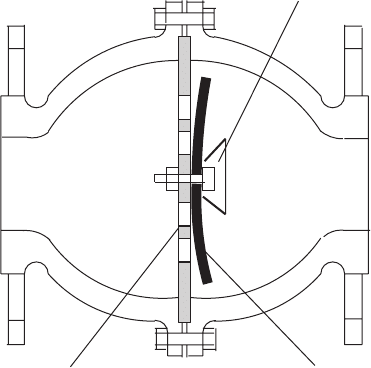
21.11 Membrane valve

The closing system for this type of valve is in the form of a ﬂexible

membrane (Fig. 21.22). During ﬂow the membrane deforms and is

held at its centre on a perforated seat. On ﬂow reversal, the mem-

brane is held against a ﬁxed diaphragm, usually of coated steel. The

diaphragm has openings of area approximating the pipe area. The

thickness and elasticity of the membrane can allow progressive open-

ing and closing, rendering this valve suitable for pulsating operation

or in systems having variable ﬂow pumps. Closure is not dependent

upon gravity and so the valve can be used in all positions. The

valve may be considered for use in circumstances where deceleration

is rapid.

434

Perforated steel seat

Flexible membrane

Steel coated grill

Fig. 21.22. Membrane valve

Pressure transients in water engineering

21.12 Prediction of valve behaviour

The variety of valve designs makes it impossible to have a standard

approach to assessment of valve behaviour. Damped valves and the

sleeve or duckbill valve can be studied by including the valve as part

of the pipeline system into which the valve is intended to be installed.

However, other valves of the free-acting type are amenable to having

their closure performance presented in the form of charts which are

independent of any speciﬁc pipeline system. This section describes

closure behaviour for a range of valve types. Many valves remain

unknown in terms of their dynamic performance and even a relatively

modest change in a documented valve’s conﬁguration can produce a

signiﬁcant change in its performance.

The potential for many patterns of check valve to produce shock

pressures following a delay in valve closure has been long recognised

and extensive studies have been undertaken to improve valve design.

As early as 1954, Livingston described studies undertaken by Glenﬁeld

and Kennedy which included measurements of the hydraulic moment

acting on swing check and tilting disk valve patterns. These studies

led to the development of the ‘recoil’ valve. The year 1959 saw con-

siderable activity in studying check valve performance with Whiteman

and Pearsal measuring closure behaviour of swing check valves at

Kingston Power Station; Worster (1959) and also Esleek and Rosser

(1959) proposed means of calculating dynamic response of a reﬂux

valve door in a decelerating and reversing water column. In 1962

Pool et al. used a modiﬁcation of the work of Esleek and Rosser and

produced good agreement between prediction and observation of

valve closure motion. Conﬁdence in their model was sufﬁciently high

for it to be used in the analysis of check valve performance in both

thermal and nuclear power plants. During his 1965 studies, Parmley

used the techniques developed by Pool et al. to predict response of

swing-check valves, Recoil valves and tilting disk valves under reﬂux

conditions. His predictions showed good agreement with observations

obtained from a transient test facility constructed by Glenﬁeld and

Kennedy. Despite these studies, problems associated with check

valves continued to occur and in his opening address to the second

Conference on Pressure Surges in 1976, Lupton (1976) appealed for

further research and development into check valves and suggested

that up to 50% of waterhammer incidents could be attributed to this

source. Since his address, numerous studies, both experimental and

numerical, have been undertaken and dynamic closure performance

of a large number of valve patterns has now been quantiﬁed. Despite

435

Check valve characteristics

the research into valve behaviour, incidents of unacceptable valve

performance still continue to occur.

Model testing plays an essential role in quantifying dynamic perfor-

mance of check valves and around the world test facilities have been

constructed which allow a check valve to be subject to varying decelera-

tion rates in order to establish how that valve will respond over a range

of operational circumstances. An early example was that of Glenﬁeld

and Kennedy and among later installations were those of CEGB at

Marchwood in England and Delft Hydraulics. Delft laboratory has

been especially active in examining different valve patterns and in

working to establish a means of presentation for test results. By testing

different patterns of valve in this way, the relative merits of each valve

can be gauged and appropriate limits of operation, in terms of allowable

gradient jdV=dtj, deﬁned. In the absence of information on dynamic

performance, check valves have often been selected on the basis of

price and availability. However, increasingly engineers are specifying

the need for ‘non-slam’ performance. ‘Slam’ refers to the noise gener-

ated on closure and is a function of the dynamic response of the

valve. However, valves come in a range of sizes. Take, for example,

the popular ‘split-disk’ type. This may be obtained in diameters ranging

from 40 mm to 1800 mm. Dynamic closure performance deteriorates

with increasing diameter and so a means of extrapolating ﬁndings

from tests on one valve size to a geometrically similar family of valve

diameters is required. Further complications may also arise, for instance

from a range of spring stiffnesses, or different properties of lever, weight

and lever/door angle, all of which can signiﬁcantly alter the dynamic

response of a valve. Mathematical modelling has a role to play by

allowing a diameter of valve which has been tested to be treated as a

model for other valve sizes.

Before any reliance can be placed upon computational models, the

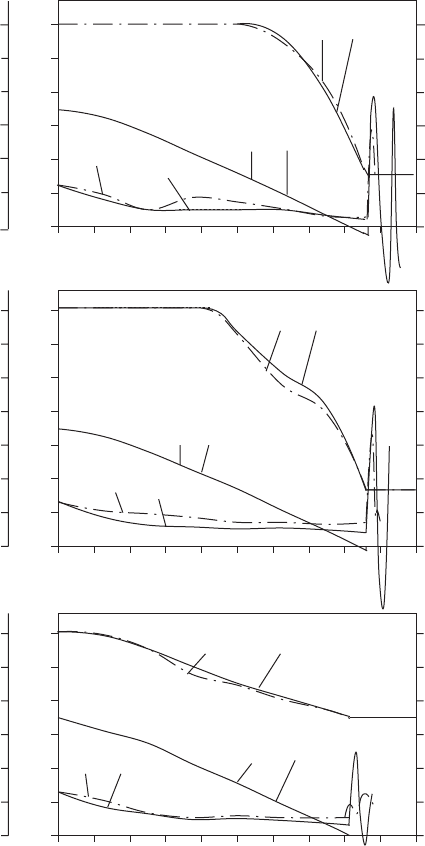
predictions must be compared with observations. Figure 21.23 shows

some typical comparisons between model predictions and laboratory

measurements for Glenﬁeld Valves of the swing check, tilting disk

and recoil patterns. These valves were all installed in a horizontal pipe-

line. In this ﬁgure, H is the pressure head just downstream of the check

valve,  is the valve door angle measured from the vertical and V is the

velocity of ﬂow in the pipe at the check valve. The subscript ‘m’ denotes

measured valves and subscript ‘c’ indicates a computed value.

A convenient means of presentation for many but not all valve types,

is to plot deceleration gradient jdV=dtj against the reversed velocity V

at the time of valve closure. Results both directly from physical testing

436

Pressure transients in water engineering

and supplemented by computational predictions have been presented

for different valve types. In any speciﬁc pipeline investigation, the

value of deceleration gradient jdV=dtj will be obtained from hydraulic

transient investigation. Entering the curve at the appropriate point

437

0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0

Swing check DN 225

H (m) q (deg) V (m/s)

Tilting disk DN 225

Recoil valve DN 225

Fig. 21.23. Measured and computed behaviour at closing check valves

Check valve characteristics

along the horizontal j dV=dtj axis using the gradient obtained by

analysis, the intercept with the appropriate curve is obtained and the

value of reversed velocity V

at closure is found.

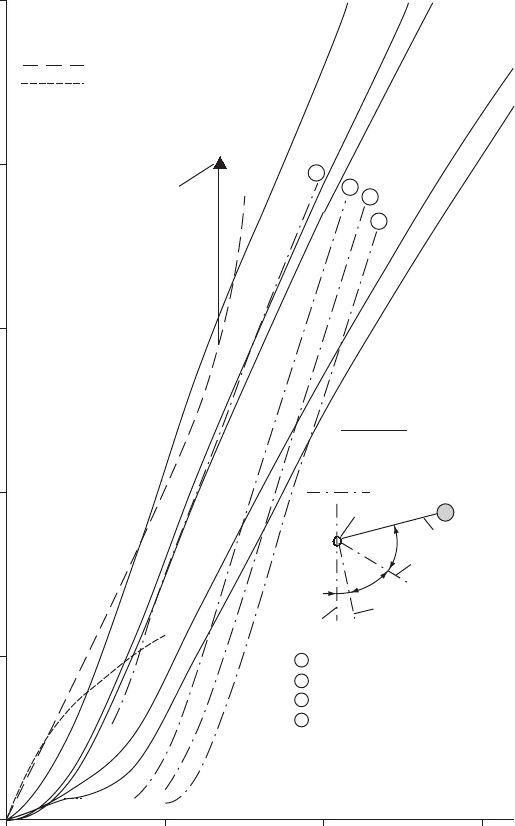
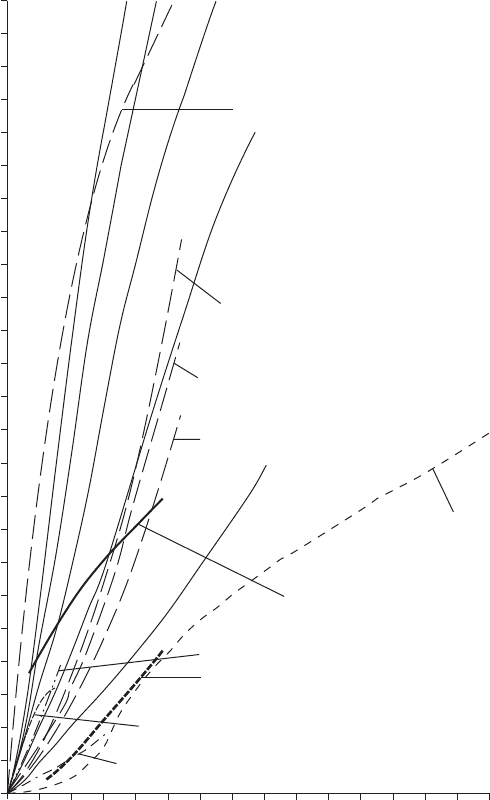
Figure 21.24 shows results from studies of swing check valves of

differing patterns. The Keystone Figure 85 is a wafer type with a seating

438

2.5

2.0

1.5

1.0

0.5

0.0

0 5 10 15

Magnitude of reversed velocity at closure (m/s)

DN 100 Delft hydraulics data

Keystone Fig. 85 DN 200

Delft hydraulics data

Effect of shifting centre of

gravity of valve door

400

300

200

250

150

Glenfield M1

Glenfield M1 DN 225

Deceleration

radient |dV/dt|

(

m/s

)

Lever length 508 mm

Vertical

1 Initial velocity 1.6 m/s no wt.

2 Initial velocity 2.7 m/s 44.53 N

3 Initial velocity 3.1 m/s 66.8 N

4 Initial velocity 3.5 m/s 92.5 N

Seat angle 16.1∞

Weighted lever

Fully open door position

40∞

44∞

Pivot

Fig. 21.24. Performance curves for swing-check valves

Pressure transients in water engineering

angle close to the vertical when installed in a horizontal pipeline. By

contrast, the Glenﬁeld M1 has a seating angle 16.18 from the vertical

in a similar installation and a 448 angle of turn to the full open position.

A spread in performance results from differences in size, opening angle

and seating angle. Valve performance deteriorates as opening angle

increases. Door weight and other factors such as a lever and weight

may also inﬂuence closure performance. When a lever and weight are

added (curves 2—4), the performance is improved for lower deceleration

rates up to around 6 m/s

but for steeper rates of retardation the effect of

additional inertia caused by the weighted lever produces deterioration

in performance. In one of many tests Provoost (1980) moved the

centre of gravity of the check valve towards the pivot and measured

a deterioration in performance as shown in the ﬁgure. Application of

swing check valves will usually be restricted to modest deceleration

gradients unless special measures are introduced such as damping of

439

Magnitude of reversed velocity at closure (m/s)

Deceleration

radient |dV/dt|

(

m/s

)

2.0

1.5

1.0

0.5

0 5 10 15

Glenfield tilting disk

DN 225

Glenfield recoil

series 5100

DN 600 recoil type

DN 300

DN 250

DN 200

DN 150

DN 100

Fig. 21.25. Performance curves for Glenﬁeld recoil and tilting disk valves

Check valve characteristics

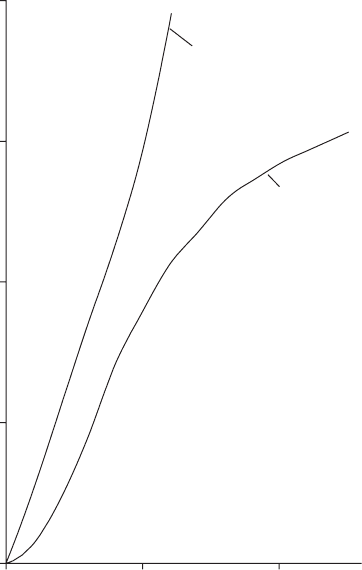
valve movement. A maximum reversed velocity <1.0 m/s would seem

reasonable.

The recoil type of valve represents a derivation of the swing check,

with a considerable improvement in performance (Fig. 21.25). The

curves shown are a combination of ﬁndings from both measurements

and computer simulations. Performance deteriorates with size, possibly

for the same reason as for the swing check with lever and weight.

Deceleration gradients of 10 m/s

or more are considered acceptable

without risk of valve slam.

Also contained in Fig. 21.25 are limited data for the Glenﬁeld tilting

disk valve DN 225. Performance of this valve is not as good as the recoil

type but has been designed to fulﬁl a different function.

Measurements from the test facility at Delft Hydraulics on the

moving ball type valve, reported by Provoost (1980, 1983), are shown

in Fig. 21.26. Closure performance is relatively poor, with substantial

440

Magnitude of reversed velocity at closure (m/s)

Deceleration

radient |dV/dt| (m/s

)

2.0

1.5

1.0

0.5

0 5 10

DN 200

from Delft hydraulics data

DN 100

from Delft hydraulics data

Fig. 21.26. Performance of moving ball valves

Pressure transients in water engineering

reversed velocity at closure attained with deceleration gradients

<5 m/s

. While other valves show a deterioration in performance

with increasing size, the curves in Fig. 21.26 show an improvement

for the large valve tested. It may be expected that ball weight and

rolling friction play some part in determining closure time, or some

441

Magnitude of reversed velocity at closure (m/s)

Deceleration

radient |dV/dt|

(

m/s

)

2.4

2.3

2.2

2.1

2.0

1.9

1.8

1.7

1.6

1.5

1.4

1.3

1.2

1.1

1.0

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0.0

0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30

Duo-chek DN 200, strong springs

Gestra BB16 DN 200 weak spring

Valve open at velocity = 0.5 m/s

Duo-chek DN 150 vertically upward flow

Duo-chek DN 200 weak springs

Gestra BB16 DN 200

super-strong springs

Valve open at velocity = 4.8 m/s

1 broken spring

Duo-chek DN 150

DN 150

Duo-chek DN 225

spring stiff = 0.01 Nm/deg

Duo-chek DN 225

spring stiff = 0.0 Nm/deg

Duo-chek DN 225

spring stiff = 0.012 Nm/deg

Duo-chek DN 225

spring stiff = 0.016 Nm/deg

DN 750

DN 600

DN 300

DN 450

Fig. 21.27. Performance of split-disk valves

Check valve characteristics