Ellis,J. Pressure transients in water engineering, A guide to analysis and interpretation of behaviour

Подождите немного. Документ загружается.

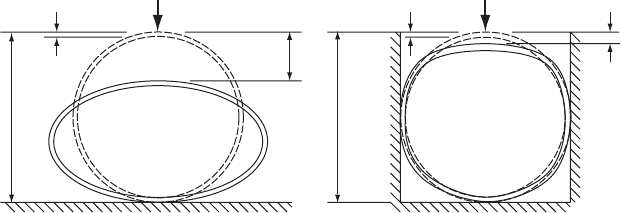
For dumped beddings and modest degrees of compaction an elliptical

deformed shape should result with horizontal deformation about 90% of

vertical. This applies to ﬂexible steel pipe as well as plastic pipes.

Deformation up to 5% of the initial outside diameter was considered

acceptable. Assuming simpliﬁed values for the supporting effect of ﬁll

and its internal friction for HDPE pipes, the vertical deﬂection

y  m was given by Hoechst Plastics (1971) as:

y ¼ 5 10

5

ðq=EÞðD

=sÞ

ð22:7Þ

where q is vertical load on the pipe N/m length and E is modulus of pipe

material N/m

Considering pipes without sideﬁll support (Fig. 22.2a), the

corresponding deformation can be calculated from:

y ¼ 22:3 10

5

ðq=EÞðD

=sÞ

ð22:8Þ

where the pipe was supported by a stiff sideﬁll (Fig. 22.2b), the deforma-

tion is given by:

y ¼ 3 10

5

ðq=EÞðD

=sÞ

ð22:9Þ

The laterally supported pipe undergoes only 13.3% of the deformation

suffered by the unsupported pipe.

22.5 Long-term buckling pressures — unconstrained

surroundings

Considering ﬁrst the case of a pipeline which is either above ground,

under water or in a trench where the ﬁll is loose or soft. Then the

deformed shape may be taken as elliptical. For ring stiffness/unit

452

s Dy

(b)(a)

Fig. 22.2. Deformed shapes for alternative side support

Pressure transients in water engineering

length of pipe:

¼ EI=r

ð22:10Þ

where I ¼ s

=12.

As regards the allowable buckling pressure within a deformed pipe

Timoshenko (1936) and others have studied the elastic stability of

cylindrical shells and predicted buckling of a round pipe using the

following equation:

¼ 24EI=½ð1 

ÞoD

ð22:11Þ

where p

is the critical buckling pressure; E is the modulus of

elasticity of the pipe material;  is Poisson’s ratio for the pipe

material, for HDPE  ¼ 0:4; I is moment of inertia of the original

circular cross-section ¼s

/12; and oD is mean outside pipe diameter.

Where out-of-roundness has occurred, a reduction factor c is applied,

giving critical pressure p

¼ p

c. Alternative expressions for the reduc-

tion factor c have been developed. These reduction factors may include

corrections both for ellipticity as well as variations in pipe wall thick-

ness. Considering ﬂexible pipes ‘creep’, effects were accounted for by

using the long-term secant modulus and long-term Poisson’s ratio for

pipe material. For a plastic pipe displaying ‘creep’, any calculation of

long-term deﬂection or buckling strength requires use of the ‘creep’

modulus. For HDPE the creep modulus at 50 years is typically 0.2—

0.3 GN/m

. When calculating initial deﬂection and strength for

HDPE, the short-term modulus is 0.8—1.0 GN/m

. The modulus for

polyethylene may be calculated from equation (22.12):

E ¼ 10:0½5:88  0:067 log

ðhoursÞ0:6 log

ð8FÞ ð22:12Þ

The reduction factor c is given variously by:

c ¼ðoD

min

=oD

max

ðs

min

max

; that is, c always <1 ð22:13aÞ

Subscripts ‘max’ and ‘min’ denote maximum and minimum values of

diameter and wall thickness.

Ignoring the inﬂuence of variations in pipe wall thickness, Allman

(1975) reported an experimentally derived expression for Alydn R ‘D’

PE pipe giving reduction factor c

as:

¼ðoD

min

=oD

max

4:62

ð22:13bÞ

Again, neglecting the effect of wall thickness changes, Gaube et al.

(1974) gave a reduction factor c

¼½ð1  Þ=ð1 þ Þ



ð22:13cÞ

453

Flexible pipe

where  ¼ D=D

is out-of-roundness. D ¼ oD

max

 oD

. Values

used are those for the pipe as received or when ﬁrst installed.

For proﬁle wall pipes then an equivalent solid wall thickness is

required for use in the equations for buckling pressure.

Above-ground mains subject to internal vacuum, or pipes subject to

external water pressure, must be designed to withstand the differential

pressure by their own stiffness. Tests on PE pipe under hydrostatic

loading show deformation to proceed progressively until at about 10%

deﬂection when the rate of deformation increases and can lead to

total collapse ( Jenkins and Krolle, 1981). This 10% deformation has

been taken as the point of failure. This study also showed strong support

for the Gaube et al. form of correction factor c

as in equation (22.13c).

22.6 Long-term buckling pressures — constrained pipelines

Where pipes were buried in compacted soil or gravel, the collapse

resistance was increased. Performance of ﬂexible pipe is determined

as much by the quality and density of compaction of the soil around

the pipe as by the properties of the pipe itself. If the buried ﬂexible

pipe is subject to internal vacuum, soil will resist the collapse. The

mechanism of buckling will be an increase in any initial deformation

of the pipe. The amount of support provided by the soil could be

calculated approximately by mathematical methods and corresponding

formulae have been proposed. For polyethylene pipes at temperatures

below 278C (808F), the chance of a pipe failure due to internal

vacuum is virtually impossible in adequately compacted soil surround-

ings.

Where the pipeline is laid in a trench and backﬁlled, the deformed

shape of pipe may be signiﬁcantly inﬂuenced by the nature of the back-

ﬁll and bedding material and on the manner of placement. When the

pipe is buried and able to take advantage of support from surrounding

soil or grout media then the pipe should resist a differential pressure

greater than that given by equation (22.11).

Allman (1975) offered an expression for buckling pressure in

constrained soil which has often been used in the absence of other data:

¼ 0:67

ðE

Þð22:14Þ

where p

is the buckling pressure in constrained soil, p

is the un-

constrained buckling pressure from equation (22.11) including any

reduction for the deformed shape, and E

is the tangent modulus of

the soil ¼

er, e being Spangler’s (1941) modulus of passive soil

454

Pressure transients in water engineering

resistance and r the pipe radius. The modulus of soil reaction E

is not a

constant but among other factors depends upon the stiffness of the pipe

used. Spangler recommended that E

values should be based upon

experience and judgement.

Equation (22.14) is acknowledged to be a relatively crude tool for

calculating collapse pressure.

Compacted soil embedment factors in the pipe zone increase pipe

resistance to hydrostatic collapse. For properly compacted embedment

areas a supporting factor fos ¼ 3 may be applied. Taprogge (1981)

calculated critical pressure p

using the relationship:

¼ p

fos ð22:15aÞ

where p

is the buckling pressure for a round pipe, fos is a factor of

safety ¼3 for properly compacted embedments, and f

is an ovality

correction factor. Table 22.3 lists values of f

as a function of  and

shows how f

varies with deﬂection.

For polyethylene sewer pipes Taprogge indicates a factor of safety

ðfosÞ¼1:5 so that the allowable differential pressure becomes:

 p ¼ p

=1:5 ð22:15bÞ

For GRP pipes the vertical deﬂection  is limited to 5%.

Greatorex (1981) has supplied data for GRP/RPM pipes and some of

his comments were as follows.

(a) In the USA GRP pipes are supplied with stiffness EI=D

¼ 1280 N/m

and this is considered close to the optimum for most applications

with a 5% deﬂection being normal. In Europe GRP pipe is supplied

with a range of stiffness.

(b) Pipes of stiffnesses < 1000 N/m

cannot be safely installed at any

depth where there is a risk of full vacuum occurring.

1100 N/m

or that obtained from the equation:

 p ¼

f32E

rtEI=D

g1=fos ð22:16Þ

where p

is external pressure; p is the internal pressure (ve if

vacuum); E

rt is the tangent value of the resultant modulus of

455

Table 22.3. Correction factor f

v. 

 (%)123456

0.91 0.84 0.76 0.7 0.64 0.6

Flexible pipe

the embendment including native soil ¼1.5E

r; EI=D

is the long-

term elastic stiffness of RPM pipe, taken to be 2/3 the initial stiff-

ness; and fos is the factor of safety. Greatorex (1981) used

fos ¼ 3 for RPM but others have used fos ¼ 2. Some values of

tr are included in Table 22.4 as a function of modiﬁed Proctor

density.

3:0  E

r  20:0MN=m

for normal embedments

Including the factor of safety ðfosÞ¼3, initial pipe stiffness and E

equation (22.16) becomes:

 p ¼

f3:56E

rEI=D

gð22:16aÞ

(d) Minimum stiffness for 1:0 D depth of cover ¼1500 N/m

(e) Minimum stiffness for installation with < 1 D depth of cover is

given by the lowest value from the equation using alternative

values of m:

 p ¼ Et=ðrðm

 1Þf1 þ½mL=ðrÞ

gÞ þ EI=½ð1 

Þr



ðm

 2 þð2m

 1 Þ=f1 þ½mL=ðrÞ

gÞ

ð22:17Þ

where r ¼ Dm=2, L is the length between pipe sockets (assuming

relatively stiff sockets), Et is the tangent modulus of passive soil

resistance, and m is the number of waves ¼1, 2, 3, . . .

(f ) With depth of cover  1:6  D the pipe may buckle under vacuum

by heaving soil upwards if the pipe is held rigidly at its sides. Pipes

are more likely to deform upwards by sideﬁll compaction during

installation and the deformation may remain under shallow

cover, especially in the absence of vehicle loading.

For SDR 18 pipes the collapse pressure was 2 unsupported value;

for SDR 32 pipes the collapse pressure was 3 unsupported value;

and where grout ﬁll was used, collapse pressure increased by ﬁve to

six times provided any gap in the grout was <1or2 D in length.

456

Table 22.4. E

tr v. modiﬁed Proctor density

Modiﬁed Proctor density 80 85 90 95

tr (MN/m

) 3.0 5.0 7.0 10.0

Pressure transients in water engineering

Kurt and Mark (1981) quoted the equation of Slocum for collapse

pressure of thermoplastic elliptical sections as:

¼ p



ð22:18Þ

where  ¼ D

min

¼ 1 .

At 5% eccentricity  ¼ 0:05 and  ¼ 0:95, giving p=p

¼ 0:63%,

and at 10% eccentricity  ¼ 0:10 and  ¼ 0:90, giving p=p

¼ 39%.

These results do not consider the stiffening effect of the reducing

minimum radius of curvature of the deforming section.

Investigations have shown that it is possible to place pipes in clay

surround and the necessary interaction between pipe and soil will be

obtained. However, the support from this clay will be less than if the

trench were reﬁlled with sand. The pipe has to be designed for its

surroundings.

Leaving aside the matter of factor of safety, the equation for long-

term buckling pressure p

 p is:

 p ¼

f32E

trEI=D

max

gð22:16Þ

This may be written in terms of the original round pipe diameter D

thus:

 p ¼ð1 "

=sÞ

1:5

f32E

trEI=D

gð22:19Þ

For long-term buckling calculations either the long-term ‘creep’

modulus E

may be used giving stiffness ¼ E

=ð12D

Þ. Alterna-

tively the long-term elastic stiffness ¼ 0:7E

=ð12D

Þ can be used.

The factor 0.7 is an adjustment for reduction in modulus over time

and may also include some compensation for out-of-roundness. The

long-term modulus is thus taken as 70% of the short-term modulus.

Equation (22.19) would indicate that if:

1  "

fð50Þ

=s ¼ 0

then the pipe will buckle under a small differential pressure p

 p, giving:

fð50Þ

¼ s=D

¼ Df

ð50Þ



ð50Þ

s=D

ð50Þ



ð50Þ

¼ 1; giving 

ð50Þ

¼ 1=Df

ð50Þ

ð22:20Þ

In the long term Df

ð50Þ

may reach values of 10—15, corresponding with

values of 

ð50Þ

in the range 6—10%. Practical experience has shown

that thin-walled pipes have collapsed after some years, even at low

backﬁll heights — that is, low values of p

 p.

457

Flexible pipe

For thicker-walled pipes Df

ð50Þ

 3 to 4, showing that 

ð50Þ

 0:25 or

25% for pipe to fail through instability. Prior to this happening however,

some thermosetting plastics such as GRP would fail due to cracking from

excessive bending strain. Soil movement would also be liable to occur.

22.7 Deformation of a circular section and its effect on wave

speed

Changes of pipe cross-sectional area due to alteration in shape are often

relatively small in comparison with the original undeformed area. In

considering the overall change of area with changing pressure, the

inﬂuence of hoop stress included in the majority of everyday pressure

transient analyses is assumed independent of the shape-change

component and these two effects are considered additive.

The act of increasing ovalisation or of partial re-rounding produces a

change in the cross-sectional area of the pipe regardless of any change in

the circumference. The term:

1=A dA=dp

which appears in the equation of conservation of mass then consists of

two components. First, there is the rate of change of area due to

changing hoop stress in the pipe wall but without shape change, as

included in elastic theory based waterhammer or pressure transient

computations. Second, there is a rate of change of area with changing

shape caused by changing internal pressure. Both of these components

will inﬂuence the rate of propagation of a pressure wave through the

composite liquid/pipe medium.

To illustrate the effect of changing shape, consider a deformed shape

having the properties:

perimeter ¼ ða þ bÞð22:21Þ

where a and b are the semi-major and semi-minor axes as shown in

Fig. 22.3.

Cross-sectional area ¼ ab ð22:22Þ

Neglecting the effect of hoop strain on the pipe circumference,

assuming perimeter length to be constant,

2r ¼ ða þ bÞ

a ¼ r þ h and b ¼ r þ v ð22:23Þ

458

Pressure transients in water engineering

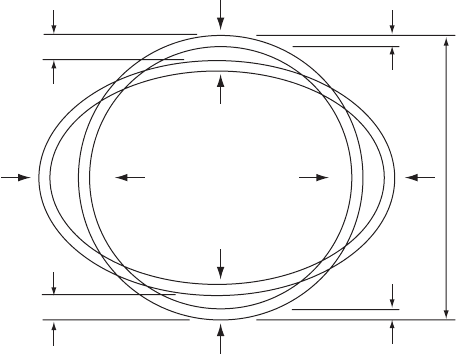
where h is the horizontal radial deviation from the circular shape and

v is the corresponding vertical deviation, then if circumference is of

constant length:

2r ¼ ðr þ h þ r þ vÞ¼2r þ ðh þ vÞ

giving,

h ¼v ¼  ð22:24Þ

Substituting in the formula for cross-sectional area A then:

A ¼ ab ¼ ðr þ Þðr  Þ¼ðr

 

Þð22:25Þ

Irrespective of the value and sign of  the cross-sectional area is

smaller than for the circular form with  ¼ 0.

Differentiating with respect to :

dA=d ¼2

and

1=A dA=d ¼2=ðr

Þ¼2=r

ð22:26Þ

From theory of elastic stability described by Timoshenko (1936), the

relationship between deﬂection and buckling pressure is given by:

=

¼ p

=ðp

 p

þ pÞð22:27Þ

459

Fig. 22.3. Deﬁnition sketch for deformation analysis

Flexible pipe

where differential pressure normal to the pipe wall is p

 p, p

being

the external pressure and p is the internal pressure;  is deformation and



is the initial deformation. p

is the differential pressure which

produces buckling in a circular section and is given by:

¼ 2E=ð1 

Þðs=D

¼ 2E=½gð1 

Þðs=D

ð22:11Þ

where h

¼ p

=ðgÞ. When p

 p ¼ p

the pipe collapses completely.

Writing:

 ¼ 

=ðp

 p

þ pÞ

and differentiating with respect to p:

d=dp ¼

=ðp

 p

þ pÞ

Assuming this is applicable to the approximately elliptical shape

under consideration, then:

1=A dA=dp ¼ 1=A dA=d d=dp ¼2=r

½

=ðp

 p

þ pÞ



1=A dA=dp ¼ 2f

=rg

=fp

 p

þ pg

ð22:28Þ

In considering the speed of propagation of a pressure wave in an

elliptically deforming HDPE outfall pipeline, Larsen (1976) derived

the expression:

ðA  A

Þ=A

¼3f

=½rðp

 p

þ pÞg

Differentiating with respect to p gives:

1=A=dA=dp ¼ 6f

=rg

=fp

 p

þ pg

ð22:29Þ

Equations (22.28) and (22.29) have different coefﬁcients, reﬂecting the

alternative assumptions with respect to the shape of deformed section

but the form of expression is the same.

Whereas the expression for changing area, at constant shape,

due to hoop stress yields a constant gradient 1=A dA=dp ¼ Dc

=ðsEÞ,

the gradient of area with pressure under changing shape is itself

pressure dependent. The pressure wave propagation rate is not a

system constant but varies with changing ﬂow conditions in a similar

manner to inclusion of gas/vapour content variation with pressure.

460

Pressure transients in water engineering

For simplicity, ignoring the effect of gas/vapour, acoustic wave speed

a now becomes:

a ¼ 1=

ðf1=K þ Dc

=ðsEÞþc

ðh

=½gðh

 h

þ hÞ

gÞ

ð22:30Þ

with pressure terms p, p

and p

having been replaced by the corre-

sponding pressure head values h, h

and h

, using h ¼ p=ðg Þ.

The changing shape factor effectively creates more storage within the

pipe than is given by simply using the area change due to hoop stress

variations. The effect is to produce a reduction in wave speed with

falling pressure and therefore a reduced pressure wave amplitude or

‘damping’ of the wave. Figure 22.4 shows the dependence of wave

speed upon ovalisation for HDPE pipes of SDR ratio 17.6 and 26.0

and for initial deformations i of 2% and 4%. Variation of the

coefﬁcient c

from 2 to 6 was also included. SDR 11 pipes are

sufﬁciently stiff to display little variation of wave speed with internal

pressure.

Larsen (1976) predicted the propagation of pressure transients

using the irregular grid of characteristics produced by varying wave

speed caused by ovalisation. While quite suitable for the relatively

straightforward case of a single pipeline without internal boundary

conditions or branches, this approach becomes more awkward for

general use. Just as the option exists of separating air or gas from the

water component when predicting wave propagation following air/gas

release under low pressures, so the same approach can be used to

separate the ovalisation factor from the area change produced by

hoop stress changes. This may be achieved by ‘collecting’ the ovalisa-

tion effect at computing sections in the same way as gas or vapour is

numerically collected. Alternatively the ovalisation effect can be

analysed as a separate pressure-dependent component distributed

along the pipeline.

Larsen (1976) was primarily interested in the use of HDPE pipes for

undersea outfalls and his concerns were largely with pipes surrounded

by water. In this context he presented curves showing how theoretical

buckling pressure varied when stiffeners in the form of anchoring

weights were placed at intervals along an HDPE pipeline. Inclusion of

pipe ovalisation would also be applicable to above-ground installations

or buried pipe where the response of the pipe was not signiﬁcantly

inﬂuenced by its surroundings. This implies soft soil surroundings

such as marsh, swamp and loose or slightly compacted ﬁll. Inﬂuence

461

Flexible pipe