Елизаров А.М. Математические методы в библиотечной работе

Подождите немного. Документ загружается.

Отметим, что при формулировке ограничений в

задачах из п. 1 — 3 встречались неравенства не только

вида (1), но и вида

(2)

или даже уравнения

а*

+ ... +

= b*

(3)

Однако любую систему ограничений (2) или (3) всегда

можно загасать в виде (1) и наоборот. (Неравенство

вида (2) сводится к (1) умножением обеих частей

на —1. Уравнение (3) эквивалентно выполнению од-

новременно двух неравенств

+ a*

... +

а*

≤

+ а*

+ .

.. +

а*

≥ b*

Заменяя каждое из уравнений (3) двумя неравенствами

и изменяя во втором неравенстве знак, снова при-

ходим к (1)).

Отметим, что от ограничений-неравенств в (1)

можно перейти к эквивалентным ограничениям в

форме уравнений. Для этого от неравенств вида (1)

перейдем к ограничениям вида

+ ... +

≥ 0.

Введем новое, так называемое добавочное неизвест-

ное

п+1

= a*

+ a*

... +

Тогда предыдущее неравенство есть просто условие

неотрицательности х

п+1

≥ 0. Если для каждого из

неравенств в (1) ввести добавочное неизвестное,

потребовав, чтобы они были неотрицательными, то

придем к системе ограничений, состоящей только из

уравнений.

В некоторых задачах иногда вместо наименьшего

значения функции f требуется отыскать наибольшее.

Но линейный характер f позволяет найти наимень-

шее значение (— f), а затем взять это значение с

другим знаком. Это и будет требуемый максимум,

иными словами, задача на максимум f также сводится

к основной.

251

Любое неотрицательное решение системы ограни-

чений называется допустимым. Допустимое решение,

дающее минимум функции f, называется оптималь-

ным. Отыскание оптимального решения и является

нашей целью. Оптимальное решение (если оно су-

ществует) не обязательно единственно: возможны

случаи, когда имеется бесконечное множество опти-

мальных решений.

§ 20. Методы решения задач линейного

программирования

В данном параграфе изучаются методы решения

основной задачи линейного программирования. Одним

из простейших способов решения является метод

перебора, когда отбираются допустимые решения и

для них вычисляется показатель эффективности.

Конечно, этот метод достаточно громоздок и зачас-

тую просто неприменим, т. к. число допустимых

решений в большинстве задач либо практически не-

обозримо, либо бесконечно. Однако модификации

метода перебора, позволяющие заранее отбросить

большее число вариантов, уже вполне применимы на

деле. Одной из таких модификаций является симплекс-

метод. Еще один метод решения, связанный с

переходом от одной задачи линейного программи-

рования к другой (возможно, более простой), заключен

в использовании так называемой теории двойствен-

ности, рассмотренной в конце параграфа.

1. Элементы линейной алгебры. Задачи линейного

программирования сводятся к рассмотрению систем

линейных уравнений и неравенств и отысканию их

решений. Подобные вопросы разрабатываются в ли-

нейной алгебре — математической дисциплине, изу-

чающей линейные операции. В данном пункте описаны

простейшие понятия линейной алгебры — координатное

линейное пространство, выпуклые множества, линей-

но-независимые системы векторов и т. д.

Известный (еще со школы) метод координат

предполагает, что каждой точке Р плоскости можно

поставить в соответствие набор действительных чисел

(х

, у

), называемых ее координатами. При этом точка

Р описывается единственным образом парой чисел

(х

, у

) и, наоборот, любой паре чисел соответствует

некоторая точка координатной плоскости.

252

Наличие координатной системы на плоскости поз-

воляет производить над точками некоторые операции,

которые имеют простую запись в координатах.

Определение 1. Суммой точек P=(x

) и

Q = (х

, у

) называется точка Р + Q = (х

+ х

, у

+ у

Произведением точки Р на число λ называется

точка λ Р=( λ х

, λ у

Введенные операции очень удобны для перевода

геометрических фактов на язык алгебры, и, наоборот,

они позволяют некоторые алгебраические соотноше-

ния интерпретировать геометрически. Начнем с опи-

сания простейших фигур на плоскости, сформулировав

без доказательства некоторые их свойства.

Отрезок, соединяющий точки P

и Р

, можно опи-

сать как множествo точек

]={P|P= λ

+ λ

}, где λ

, λ

≥0,

+ λ

=1.

Треугольник с вершинами в точках P

, Р

и Р

может быть задан как множество точек

ΔР

= {Р|Р = λ

+ λ

}, где λ

, λ

≥0,

+ λ

=1. (1)

Если λ

= 0, то точка Р, задаваемая в (1), описывает

отрезок [Р

], являющийся стороной треугольника;

если же λ

= 0 или λ

= 0, то Р описывает [Р

] или [P

]

соответственно.

Прямая, проходящая через точки P

, y

) и

, y

), также может быть описана как множество

точек Р(х, у),

P = λ

+ λ

тде λ

+ λ

= 1, но λ

, λ

уже должны быть произволь-

ными числами. При атом координаты х, у удовлетво-

ряют уравнению ах + bу = с, где а = 1/(х

—х

b = 1/ (у

— y

), с = х

/ (х

— х

) — у

/ (y

- у

Таким образом, мы пришли к следующему заклю-

чению: координаты точек, лежащих на прямой линии,

удовлетворяют линейному уравнению с двумя неиз-

вестными. Это наблюдение представляет собой пример

перевода геометрического факта на алгебраический

язык. Изучение прямых на плоскости оказывается

эквивалентным изучению линейных уравнений первой

степени. Однако указанный дуть допускает обратную

253

Рис. 70. Полуплоскость

процедуру, а именно: геометрическую интерпретацию

алгебраических соотношений.

Выясним теперь, какое множество на плоскости

образуют точки, координаты которых удовлетворяют

неравенству ах + by ≤ с. Ответ на этот вопрос при-

водит нас к геометрическому понятию полуплоскости.

Если b ≠ 0, то данное неравенство приводится к виду

у ≥ kx + l или у ≥ kx + l. Понятно, что первому из

неравенств удовлетворяют точки, лежащие над прямой

у = kx +l или на ней, а второму—все точки, лежащие

под этой прямой или на ней. Если же b = 0, то нера-

венство приводится к виду х ≥ т или х ≤ m. Послед-

ним условиям удовлетворяют точки, лежащие правее

или левее прямой х = т или на самой прямой (рис. 70).

Итак, полуплоскость определяется как множества

точек плоскости, координаты которых удовлетворяют

неравенству ах + by ≤ с.

Выпуклые множества и крайние точки. При опре-

делении точек отрезка [P

] была введена линейная

комбинация точек Р

и Р

, задаваемая как точка

P = λ

+ λ

, λ

≥ 0, λ

+ λ

= 1.

Мы видели, что любую точку отрезка можно было

представить как линейную комбинацию концов от-

резка. Аналогичное построение было осуществлено

и для треугольника, который представлялся как

линейная комбинация точек P

, P

и Р

. По аналогии с

этими случаями введем

Определение 1. Точка Р называется линей-

ной комбинацией точек P

, P

, ..., Р

, если

Р = λ

+ λ

+ ... + λ

где λ

, λ

, ..., λ

≥0 и λ

+ λ

+ ... + λ

= 1.

254

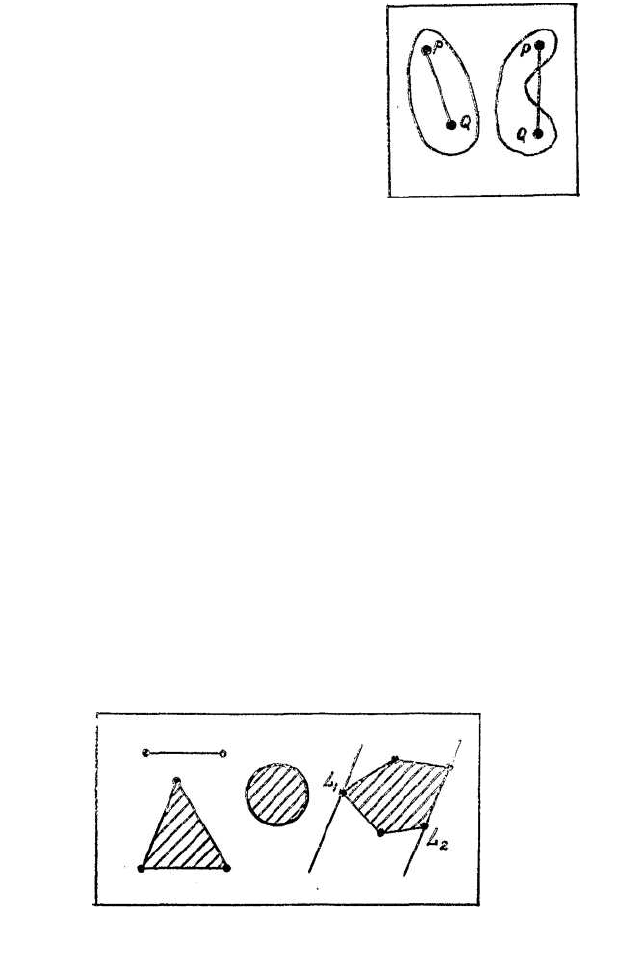
Как отрезок, так и треугольник

представляли собой примеры

множеств, которые вместе с лю-

быми двумя точками содержали

отрезок, соединяющий эти точки.

В математике такие множества

принято называть выпуклыми.

Определение 2. Множество

называется выпуклым, если

вместе с любыми двумя точками

оно содержит их произвольную

линейную комбинацию.

Примерами выпуклых множеств также являются

прямая, полуплоскости, круг и т. д. (см, рис. 71).

Введем еще одно важное понятие, обобщающее

понятие вершин треугольника и концов отрезка.

Определение 3. Крайними точками выпук-

лого множества называются точки, которые нельзя

представить в виде линейной комбинации двух дру-

гих точек этого множества.

Например, крайними точками отрезка являются

его концы, крайними точками треугольника — его

вершины, крайними точками круга — все точки

окружности, ограничивающие этот круг, и т. д. Как

видно из примеров, выпуклое множество может иметь

как конечное, так и бесконечное число крайних точек.

В то же время прямая или плоскость крайних точек

не имеют.

Определение 4. Опорной прямой выпуклого

множества называется прямая, имеющая с этим

множеством, расположенным по одну ее сторону,

хотя бы одну общую крайнюю точку.

Рис. 72. Крайние точки и опорные прямые

255

Рис. 71. Выпуклое и

невыпуклое множества

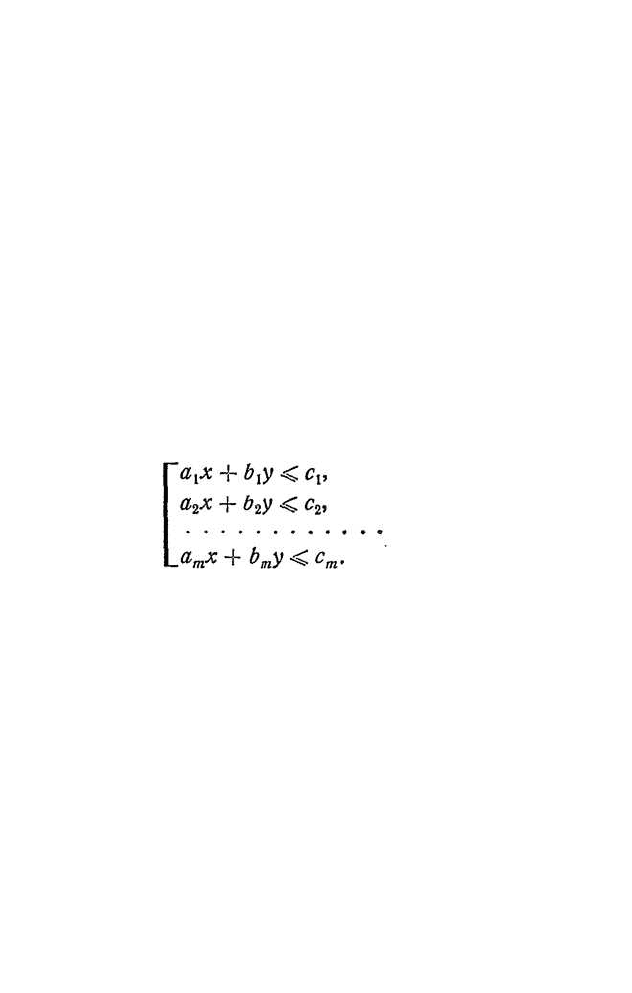
Например, прямые L

и L

на рис. 72 являются

опорными. Одно из наиболее важных свойств выпук-

лых множеств описано в следующей теореме, приводи-

мой без доказательства.

Теорема 1. Пересечение любых двух выпуклых

множеств есть выпуклое множество.

Сейчас мы изучим класс выпуклых множеств на

плоскости, который имеет особое значение в теории

линейного программирования.

Определение 5. Выпуклым многоугольником

называется выпуклое множество плоскости, имею-

щее конечное число крайних точек.

В линейной алгебре доказывается, что ограничен-

ный выпуклый многоугольник может быть представ-

лен как линейная комбинация своих крайних точек

(случай отрезка и треугольника мы разбирали выше).

Этот факт будет необходим для геометрической ин-

терпретации решения систем линейных неравенств, к

которой мы сейчас переходим.

Обратимся к описанию области решений системы

линейных неравенств с двумя неизвестными x и у

(2)

Так как уравнения а

x + b

у = c

(k = 1, 2, ..., т)

определяют прямые в плоскости, то каждое неравен-

ство системы определяет одну из полуплоскостей,

на которые соответствующая прямая разбивает всю

плоскость. Если пара чисел (х, у) удовлетворяет всем

неравенствам системы, то соответствующая точка

Р(х, у) принадлежит всем указанным полуплоскостям, т.

е. их пересечению. Иными словами, область решений

системы линейных неравенств М образуется путем

пересечения полуплоскостей, задаваемых каждым

неравенством системы (рис. 73).

Пересечение любых двух полуплоскостей, являю-

щихся выпуклыми множествами, также является в

силу теоремы 1 выпуклым множеством. Поэтому

можно утверждать, что область М решений системы

является выпуклым множеством. Сразу отметим, что

область M не всегда является ограниченным выпук-

лым многоугольником (см. рис. 73). В том случае,

256

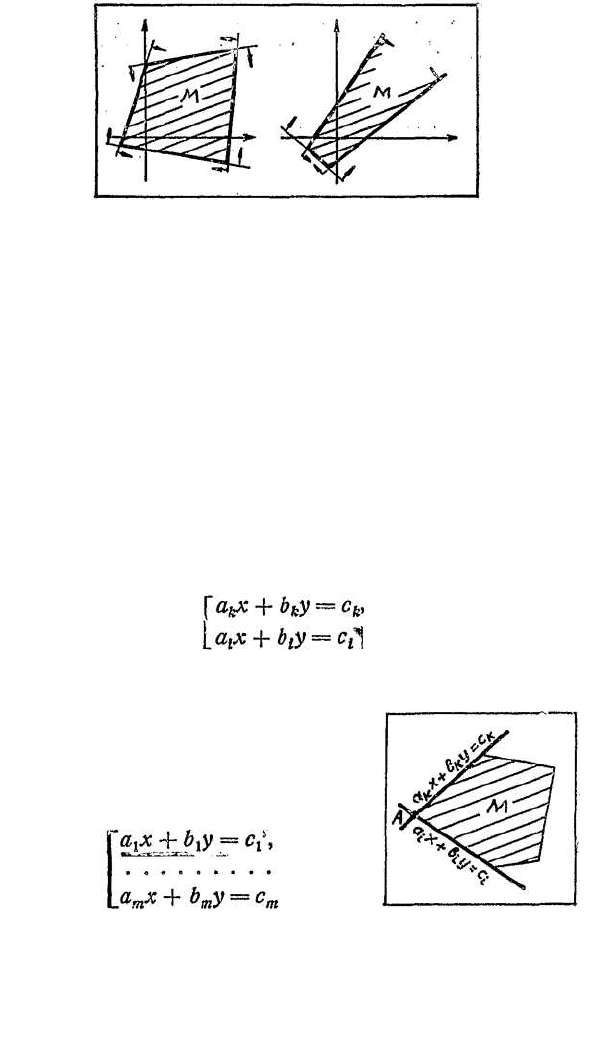
Рис. 73. Область решений системы

когда множеетво М не пусто, говорят, что система

линейных неравенств совместна. Мы уже отмечали,

что знание крайних точек, позволяет представить

ограниченный выпуклый многоугольник как линейную

комбинацию своих крайних точек. Сейчас мы опишем

способ нахождения крайних точек области решений

системы. Так как каждому неравенству соответствует

полуплоскость, граничная, прямая которой

определяется уравнением а

x + b

y = с

, то точка А из

области М в том и только в том случае является

крайней точкой, когда она принадлежит двум

различным прямым (рис. 74). В элементарной алгебре

доказано, что прямые, задаваемые уравнениями a

x +

y = c

и a

х + b

у = с

, различны, (и пересекаются

в единственной точке), если система

имеет единственное решение. Такие системы назовем

правильными. Теперь можно описать способ нахож-

дения крайних точек области M:

чтобы найти все крайние точки,

необходимо найти решения всех

правильныx подсистем из двух

уравнений системы уравнений

и отобрать из них те, которые

удовлетворяют исходной системе

неравенств.

17 Т-743

Рис. 74. Крайние точ-

ки системы

257

Поскольку число правильных подсистем исходной

системы конечно, то конечно и число крайних точек

области М. Таким образом, мы приходим к следую-

щему утверждению.

Teopeмa 2. Область решения системы линейных

неравенств (2) представляет собой выпуклый

многоугольник М, получающийся в результате пере-

течения всех полуплоскостей, отвечающих неравен-

смвам данной системы.

Для описания положения точки на плоскости

достаточно двух координат (х, у), но если описывать

положение точки в пространстве, то уже необходимо

задавать три координаты (х, у, z). Если к тому же

следить за перемещением этой точки с течением

времени, то полное описание потребует знания четырех

чисел (х, у, z, t) — трех координат и момента времени. В

физике, экономике, технике часто изучают объекты

для задания которых недостаточно двух или трех

координат. Поэтому целесообразно обобщить метод

координат на случай произвольного координатного

пространства.

Назовем упорядоченный набор из п действительных

чисел x

, x

, ..., х

точкой n-мерного пространства и

обозначим через Р = (x

, x

, ..., х

). Числа х

назы-

ваются координатами точки. В одномерном случае

мы получаем точки на прямой, в двухмерном — точки

на координатной плоскости и т. д.

Множество n-мерных векторов образует линейное

пространство R

. Простейшими множествами в R

являются отрезок, соединяющий точки P

€R

(т. е. множество {P€R

|P = λ

+ λ

}, λ

+ λ

=1), а полупространства, определенные

неравенствами вида а

+ ... + а

≥ b.

Понятие выпуклости также обобщается на n-мер-

ный случай. Как и в случае R

, множество точек из

называется выпуклым, если вместе с любыми двумя

точками оно содержит весь отрезок, соединяющий

эти точки.

В дальнейшем нам понадобится свойство, которое

мы формулируем без доказательства в следующем

виде.

Теорема 3. Любое полупространство является

выпуклым множеством.

258

Теперь мы готовы дать геометрическую интерпре-

тацию системы линейных неравенств с п неизвестны-

ми вида

(3)

Каждое из неравенств системы определяет некоторое

полупространство. Все неравенства совместно опре-

деляют некоторую область М, образованную путем

пересечения полупространств, задаваемых каждым

неравенством системы. Так как все полупространства

выпуклы, то область М, получившаяся в результате

пересечения, также является выпуклым множеством.

Как и в двухмерном случае, выпуклое множество

называется выпуклым многогранником, если оно

имеет конечное число крайних точек. Метод отыска-

ния крайних точек множества М, получившегося в

результате пересечения полупространств, также можно

обобщить по аналогии с двухмерным случаем, однако

мы на этом не останавливаемся. Отметим лишь, что

число крайних точек конечно; это приводит нас к

следующему утверждению.

Теорема 4. Область решений системы линейных

неравенств (3) представляет собой выпуклый много-

гранник М, составленный из точек пространства

, координаты которых удовлетворяют системе.

Определение 2. Система векторов P

, ..., Р

называется линейно зависимой, если найдутся та-кие

числа λ

, λ

, ..., λ

, не все равные нулю, что имеет место

равенство

+ λ

+ ... + λ

= 0.

В противном случае система называется линейно

независимой.

2. Решение общей задачи. Напомним формулировку

основной задачи линейного программирования. Дана

система линейных ограничений (в виде уравнений)

(4)

259

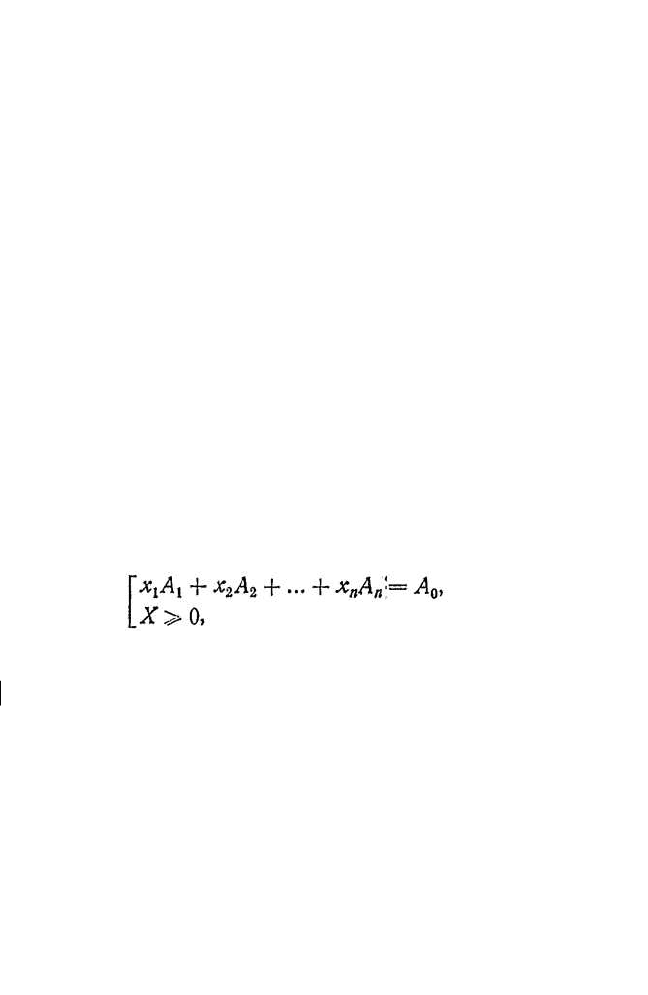
и линейная функция f = с

+ с

+ ... + с

. Требуется

найти такие неотрицательные значения х

≥ 0, x

≥ 0, ...,

≥ 0, при которых функция f принимает наименьшее

значение.

Геометрическая интерпретация. Как уже отмеча-

лось в п. 1, область решений системы линейных

уравнений (4) представляет собой выпуклый много-

гранник допустимых решений. Поэтому геометри-

чески решение задачи линейного программирования

представляет собой отыскание такой точки много-

гранника решений, координаты которой доставляют

линейной функции минимальное значение. Эта точка и

представляет собой оптимальное решение.

В теории линейного программирования доказана

важная

Теорема 5. Линейная функция задачи линейного

программирования достигает минимального значения

в крайней точке выпуклого многогранника решений.

Если эта функция принимает минимальное значение

более чем в одной точке, то она достигает того

же значения в любой точке, являющейся линейной

комбинацией этих крайних точек.

Таким образом, для решения задач линейного

программирования важно уметь отыскивать крайние

точки. Опишем общий способ нахождения этих точек.

Для этого перепишем систему ограничений в виде

(5)

где А

= (а

, а

, ..., а

), ..., А

= (а

, а

, ..., а

= (b

, ..., b

), X = (x

..., x

). Справедлива следую-

щая общая

Теорема 6. Если система векторов А

, ..., А

(т ≤ п) в

представлении системы ограничений (5) линейно

независима и такова, что х

+ ... + х

= А

и все

≥ 0, то точна Х

== (х

, х

, ..., х

, 0, ..., 0) является

крайней точкой многогранника решений. Если Х = (x

..., x

) — крайняя точка многогранника ре-шений, то

векторы в разложении (5), соответствую-щие

положительными x

, линейно независимы.

В простейшем случае с данной теоремой мы по-

знакомились в п. 1 при описании способа нахождения

крайних точек области М; в общем случае доказа-

тельство теоремы гораздо более сложное. Теорема 6

260