Елизаров А.М. Математические методы в библиотечной работе

Подождите немного. Документ загружается.

отношения между затратами на функционирование

системы и потерями потребителей из-за ее несовер-

шенства, то критерий оценки комплектования можно

взять в виде

F = S + R

G, (1)

где S — стоимость, затраченная на достижение цели, а

G—эффективность. Коэффициент R

служит для

согласования величин S и G. Рассматриваемый кри-

терий хорош тем, что включает в себя затраты всей

системы. Чем меньше значение F, тем эффективнее

проведено комплектование. Трудность состоит в оп-

ределении значений S, R

, G. Стоимость библиотечных

операций можно определенным образом оценить.

Эффективность затраченной на формирование фонда

стоимости, как правило, оценивают числом отказов

или средним временем удовлетворения запроса. Пос-

ледний показатель является более общим, т. к. пред-

полагает оценку всей системы, а не одного фонда.

При этом коэффициент R

будет характеризовать по-

тери в единицу времени, которые несет потребитель

в процессе ожидания. Единого подхода к определе-

нию величины R

пока нет. Опишем один из извест-

ных способов.

Рассмотрим модель распределения времени потре-

бителя в процессе творческой деятельности с момента,

когда он узнал о существовании документа, способного

ускорить решение стоящей перед ним задачи. Пусть в

начальный момент времени t

потребитель делает

запрос и приступает к работе с тем, чтобы закончить

ее за время t . В момент t

= t

+ Т (T — среднее время

удовлетворения запроса) он получает документ и

продолжает работу, заканчивая ее за время

= t

+ (1 —t

/ t

), где t

— среднее время, за которое

потребитель выполнил бы работу, если бы в момент t

знал информацию из документа, t

— среднее, время, за

которое он выполнил бы работу, не имея этой

информации. Итак, затраты потребителя из-за

несовершенства системы есть з = g (1 — t

) T, где

g — средняя заработная плата. Если оценить, как ус-

ловлено, эффективность системы средним временем

удовлетворения запроса, то R

= g (I — t

/ t

). Величина

/ t

меняется в интервале от 0 до 1 и определя-

14* 211

ется характером научной или производственной дея-

тельности абонентов.

Выбор того или иного критерия оценки эффектив-

ности комплектования фонда позволяет построить

соответствующую этому критерию математическую

модель определения экземплярности издания в фонде.

Опишем такую модель для критерия (1). Задача сос-

тоит в определении такого количества М экземпляров

конкретного издания, чтобы оптимизировать данный

критерий.

Будем предполагать, что при наличии в фонде не-

виданного экземпляра время ожидания равно нулю.

В данном случае критерий (1) принимает вид

F=M•Q +R

Tλ. Стоимость S определяется как затраты

на приобретение, обработку и хранение искомого

количества экземпляров М, а эффективность G —

как суммарное время ожидания потребителями

документов при λ обращениях. Время ожидания можно

оценить в стоимостном выражении исходя из катего-

рий зарплаты абонентов. Специально нужно исследо-

вать вопрос, какую часть этого времени считать не-

производительной. Есть мнение, что задержка в 2—3

дня ведет к потере 2—3 часов рабочего времени.

Будем считать, что R

имеет размерность руб/час

и лежит в интервале [0, 1]. Величину R

выбирает

исследователь исходя из финансовых возможностей

данной библиотеки.

Рассмотрим систему массового обслуживания

„с ожиданием" (см. гл. 4), где каналами обслуживания

являются экземпляры документа, процесс обслужива-

ния заключается в получении абонентами информации,

а дисциплина обслуживания такова: первым пришел,

первым обслужили. Известно, что входной поток

заявок нестационарен и пиковая его интенсивность

приходится на первые годы после издания документа.

Потом документ стареет, интенсивность падает. Нас

интересует начальный момент, для него и рассчитаем

экземплярность. Предположим, что в этот момент

поток читательских требований будет простейшим

с интенсивностью λ. Время обслуживания Т — случай-

ная величина, подчиненная показательному закону

распределения с параметром и

= 1/Т. Из результатов

теории массового обслуживания вытекает справедли-

вость следующей формулы:

212

где α = λ/и

и предполагается, что α<М. Зная зави-

симость Т = Т (М), определяемую выписанной форму-

лой, нетрудно найти оптимальное (по данному кри-

терию) значение М, при котором значение F мини-

мально.

Экземплярность книг и брошюр в фонде можно

рассчитать, используя формулы Эрланга (см. п. 5 § 15).

Для такого расчета необходимо определить интен-

сивность потока заявок λ на каждое конкретное наи-

менование изданий (в принципе, при практических

расчетах под интенсивностью потока заявок можно

понимать среднюю обращаемость части фонда, со-

держащей данное издание). Значение 1/и

среднего

времени обслуживания одной заявки определяется

условиями работы каждой конкретной библиотеки и

заранее известно. Величина α = λ/и

— это „приведенная

интенсивность" потока заявок, представляющая собой

среднее число заявок, приходящихся на среднее время

обслуживания одной заявки. Из формул Эрланга

следует, что если все п экземпляров книги выданы, то

заявка получает отказ с

вероятностью p

/n! где р

= —ве-

роятность того, что все экземпляры данной книги

находятся на полке. Вероятность того, что читатель

получает потребованное издание, есть q = 1—р

Среднее количество выданных экземпляров можно

вычислить по формуле =aq. Для определения эк-

земшшрносга n нужно задать максимальную вероят-

ность отказа. Как правило, это требование выражается

неравенством р

≤ 0,15.

Для сравнения теоретических результатов с дан-

ными, полученными в результате изучения читатель-

ских интересов, можно использовать формулу

Э = At/T

, где Э — экземплярность, А — число чи-

тателей книги, t — средний срок использования книги

одним читателем (в днях), определяемый либо опыт-

213

ным путем, либо из правил пользования библиотекой,

а Т

— время активной жизни книги (в днях), опреде-

ляемое прогностически.

При оценке эффективности формирования фонда

вместо критерия (1) могут быть использованы неко-

торые другие критерии, учитывающие в первую оче-

редь те показатели, которые являются определяющими

в проводимом исследовании. Остановимся еще на

одном примере такого типа.

Так как система показателей эффективности в пер-

вом приближении состоит из показателей количества,

качества и экономичности, расчленим показатель об-

щей эффективности на составные части F = α

кол.

+ α

кач.

+ α

экон.

, где α

, α

— весовые коэффициенты, α

+ α

= 1. Показателями количественного характера

кол.

считаем представительность фонда k

пpедcт.

коэффициенты обращаемости и книгообеспе-ченности.

Представительность фонда определяется формулой

предст.

=Р

вып.

/Р

биб.

и выражает долю из выпускаемых

изданий по определенной тематике, приобретенных

библиотекой.

К показателям качественного характера относятся:

профильность фонда k

проф.

, коэффициент читаемости,

средний возраст фонда, оперативность формирования,

Профильность фонда — число, показывающее, какая

доля из приобретенных изданий соответствует про-

филю фонда, т. е. k

проф.

= P

биб.

/ Р

темат.

. Средний возраст

фонда — это среднестатистический год издания, рас-

считанный по всему фонду.

Показатели экономического характера — общая

стоимость фонда на одного реального (или потен-

циального) абонента и средняя стоимость одной пе-

чатной единицы. Ряд других показателей эффектив-

ности комплектования приведен в ([22], гл. 3, п. 2).

Наконец, при оценке эффективности комплектова-

ния можно использовать закон Брэдфорда (см. п. 3

§ 16). Действительно, т. к. количества изданий в ядре

и последующих зонах соотносятся как 1:п:п

:... , то

для удовлетворения всех читательских запросов тре-

буется фонд в 5—10 раз больший, чем для удовлетво-

рения 75% запросов. Фонд можно считать укомплекто-

ванным оптимально и по составу, и по величине

214

если им удовлетворяется 75—80 % от общего числа

требований.

В заключение настоящего пункта остановимся на

вопросе прогнозирования обращаемости книг неко-

торой группы. Хотя средняя обращаемость О (t) с

течением времени по всем книгам некоторого класса

может изменяться довольно слабо (поскольку более

старые книги с уменьшающимися показателями обра-

щаемости непрерывно заменяются новыми), ясно, что

средняя обращаемость по фиксированной выборке

книг должна убывать со временем. Простейшая ве-

роятностная модель, позволяющая учесть зависимость

обращаемости от времени, описывается марковскими

процессами (см. § 15). Это означает, что обращаемость

О в конце данного промежутка времени целиком оп-

ределяется обращаемостью в начале этого промежутка.

Так, если документ выдавался т раз в течение года,

то случайная величина, характеризующая его обра-

щаемость в следующем году, будет иметь вероятност-

ное распределение, выражающееся через т и лишь

неявно зависящее от обращаемости документа в пре-

дыдущие годы.

Рассмотрим набор документов, имеющий в неко-

тором году среднюю обращаемость O(t). Согласно

модели, его средняя обращаемость О (t +1) в сле-

дующем году должна зависеть лишь от O(t). Пусть

— условная вероятность перехода от обращаемости

т в предыдущем году к обращаемости п в рас-

сматриваемом. Имеем Р

т,0

+ Р

т,1

+ ... = 1. Если набор

документов имел обращаемость т в году t, то его

средняя обращаемость 0(t+1) в (t+1)-м году вы-

разится так:

О(t + 1) = 0•P

m,0

+ 1•P

m,1

+ 2•P

m,2

+ ...

Как было показано экспериментально, для конкретных

библиотечных фондов средние обращаемости в t-м

и (t + 1)-м годах связаны соотношением

О(t+1)=α+ β 0(t), β <1, (2)

где αи β — параметры, характеризующие данный фонд.

Параметр β характеризует скорость убывания интepeca

к фонду, а α — асимптотическое значение обращае-

мости, которого рано или поздно достигает средняя

215

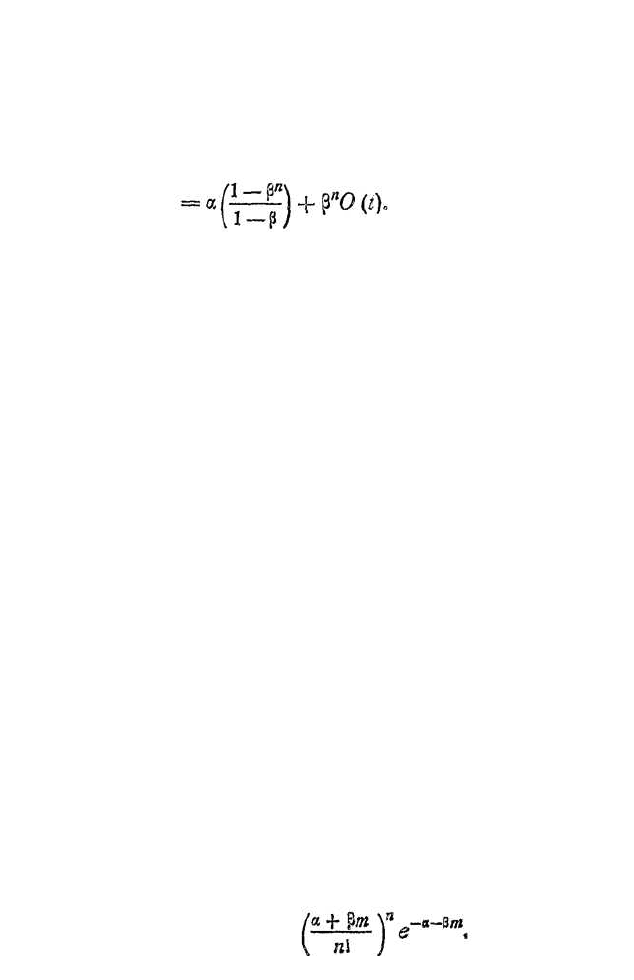
обращаемость старых книг фонда. Когда β намного

меньше 1, обращаемость резко падает. Обычно

0,2≤β≤0,8 и параметр β остается приблизительно

постоянным в течение 10 лет, тогда как 0,3≤α≤0,7

и медленно убывает с каждым годом. Из уравнения (2)

выводим

О(t + n) = α + αβ + αβ

+ ... + αβ

n-1

+ β

O(t) =

(3)

Изучение обращаемости некоторой совокупности биб-

лиотечных материалов проводится в два этапа:

1) собираются статистические данные по обра-

щаемости, и эмпирическое вероятностное распределе-

ние отождествляется с полученными частотными дан

ными;

2) первоначальное распределение вместе с мар-

ковской моделью используется для прогноза обра-

щаемости.

Первый этап не всегда прост, т. к. обращаемость

изменяется в зависимости от времени и обстоятельств,

а также потому, что единственное выбранное эмпи-

рическое распределение не может должным образом

характеризовать все классы библиотечных материалов.

Например, имеются данные, показывающие, что по-

ведение книг „нулевого спроса" не подчиняется ни-

какому из известных распределений (пуассоновскому,

геометрическому и т. д.). При таких обстоятельствах

некоторые классы книг требуют специального иссде-

дования.

Опыт показывает, что в большинстве ситуаций

удовлетворительные результаты дает геометрическое

распределение (см. § 10) при надлежащем выборе его

параметров. Если допустить, что обращаемость до-

кументов случайна по природе, то ее частотные ха-

рактеристики достаточно хорошо согласуются с пу-

ассоновским распределением. Если в году t имеем

O(i\t) = m, то при пуассоновском распределении веро-

ятность того, что О (t + 1) = п, определяется форму-

лой

m,n

= Р

(α + βm) =

216

Выписанные фoрмулы, прогнозирующие обращаемость

книг в фонде, используются при вторичном отборе.

Подсчитаем ожидаемую обращаемость О

нулевого

(единственного) экземпляра документа. Имеем: О

есть время, на которое книга будет выдана (напом-

ним, что через 1/u

в теории массового обслуживания

мы обозначили среднее время обслуживания одной

заявки, а через и

— интенсивность прибытия заявок,

= λ — для простейшего потока). За это время по-

студит и

/и

заявок, которые окажутся неудовлетво-

ренными. Тогда число удовлетворенных за это вре-

мя требований (т. е. искомая обращаемость) есть

= и

- u

/и

или О

= и

/(и

+ и

). (4)

Если имееуся второй экземпляр книги, обращаемость

единственного экземпляра которой равна О

, то второй

экземпляр будет выдаваться примерно О

(О

/и

) раз, где

/и

— доля времени, в течение которого

предполагаемый абонент не найдет первый экземпляр

книга на полке. Если O

не слишком велико (≤1/2),

то общая обращаемость обоих экземпляров будет

приблизительно равна

= О

+ О

/и

. (5)

Из этой формулы видно, что при очень малых O

второй экземпляр мало полезен.

4. Вторичный отбор осуществляется в уже имею-

щемся фонде в целях обеспечения его соответствия

задачам библиотеки и интересам ее читателей. В про-

цессе вторичного отбора решают, какие издания сле-

дует оставить в фонде для их дальнейшего исполь-

зования и какими изданиями следует доукомплекто-

вать фонд.

Для выработки рекомендаций по приобретению

дублетов можно пользоваться моделью расчета обра-

щаемости из предыдущего пункта. В частности, фор-

мула (5) дает выражение ожидаемой обращаемости

для двух экземпляров книга. Решение о приобретении

дублетов может быть основано на прогнозируемой

величине возрастания обращаемости на будущие годы

по следующей схеме:

а) исходя из обращаемости 0(1) в 1-м году, из

уравнений (3) находим значения 0(2), 0(3) на после-

дущие годы;

217

б) значение 0(1) для единственных экземпляров

определяем по формуле (4);

в) вводим дополнительный показатель обращае

мости О

(1)/и

для дублетов;

г) вычитая из полной обращаемости документа

обращаемость его дублета и сравнивая эти разности

с характерными показателями обращаемости (напри-

мер, со средней обращаемостью по всем документам

библиотеки), даем рекомендации о приобретении дуб-

лета, если предполагаемое увеличение показателя об-

ращаемости превосходит некоторое выбранное поро-

говое значение.

Приобретение новых документов требует решения

проблемы их размещения и хранения. Стабильная

ситуация достигается в том случае, когда интенсив-

ность потока вновь приобретаемой литературы ста-

новится равной интенсивности потока удаляемой ли-

тературы. Среди прочих, не поддающихся измерению

факторов, влияющих на решение об удалении доку-

мента, следует отметить наличие дублетов или других

документов на ту же тему.

Среди количественных показателей для оценки

важности документа особенно интересны следующие:

а) возраст документа (количество лет со дня его

первого издания);

б) количество ссылок на данный документ в позд-

нейшей литературе;

в) используемость документа, измеряемая коли-

чеством выдач или длительностью срока пользования.

Все эти показатели (кроме возраста) обычно не

имеют универсального значения и решение об удале-

нии документа во многих случаях принимается на

основании неполной информации. Все существующие

модели удаления документов основаны на вычислении

старения документа — показателя, характеризующего

падение спроса на документ с течением времени.

В большинстве случаев используется первоначальное

допущение (провереннее экспериментально), что ин-

тенсивность использования убывает со временем

экспоненциально, например, R (t) = R

ехр (—tа), где R

(t) — суммарное количество ссылок на документы

возраста t и более, R

— количество ссылок на все

документы массива, а — возрастной множитель, зави-

сящий от предметной области. Разрешая выписанное

218

соотношение при фиксированных значениях R

и а

можно определить время t, за которое общее число

ожидаемых ссылок сократится до половины (или до

четверти, или до десятой части), что в свою очередь

может определять политику удаления документов из

фонда. На практике такая модель все же не является

достаточной для определения политики удаления, т. к.

документы различной важности в смысле закона Брэд-

форда, по-видимому, должны удаляться в различные

моменты времени. Следовательно, нужно комбиниро-

вать характеристики важности журналов, измеряемые

количеством опубликованных в них релевантных ста-

тей, с моделями прогнозирования обращаемости, оце-

нивающими ожидаемый спрос, и с моделями опреде-

ления количества ссылок на данный документ.

Большинство вычислений старения документов вы-

полняется не в экспоненциальной модели, а в эквива-

лентной геометрической модели u(t)=а

u(0), а<1, где

u(t)—общее количество ожидаемых ссылок на статьи

из данного множества журналов по прошествии t лет,

и (0) — общее количество ожидаемых ссылок начиная

с настоящего времени. Такая модель основана на

предположении, что если имеется С ссылок в течение

первого года, то в течение второго года будет Са

ссылок, в течение третьего — Са

и т. д. Тогда,

и (0) = С (1 + а + а

+ ...), и (t) = Са

(1 + а + а

+ ...).

откуда и выводится указанная выше зависимость

Данную модель можно положить в основу стратегий

удаления, если условиться списывать документы, для

которых отнощение „остаточной полезности" u(t) к

первоначальной и(0) достигает порогового значения

, т. е. когда а

≤T

Часто для оценки темпов старения подсчитывается

„годовой коэффициент старения" а

, получаемый как

отношение частоты использования документа в тече-

ние какого-либо года С

к частоте использования в

предыдущем году С

: а

= C

. Если под исполь-

зованием понимать наличие ссылки, то а

= а. Б. Брукс

ввел „общий коэффициент полезности" u = 1/(1— a

Идеальной схемой проведения наблюдений за старе-

нием какой-либо совокупности документов, появив-

шихся в году t, было бы измерение частоты исполь-

зования этой совокупности в первый (t +1), второй

(t + 2), третий (t + 3) и последующие годы вплоть до

219

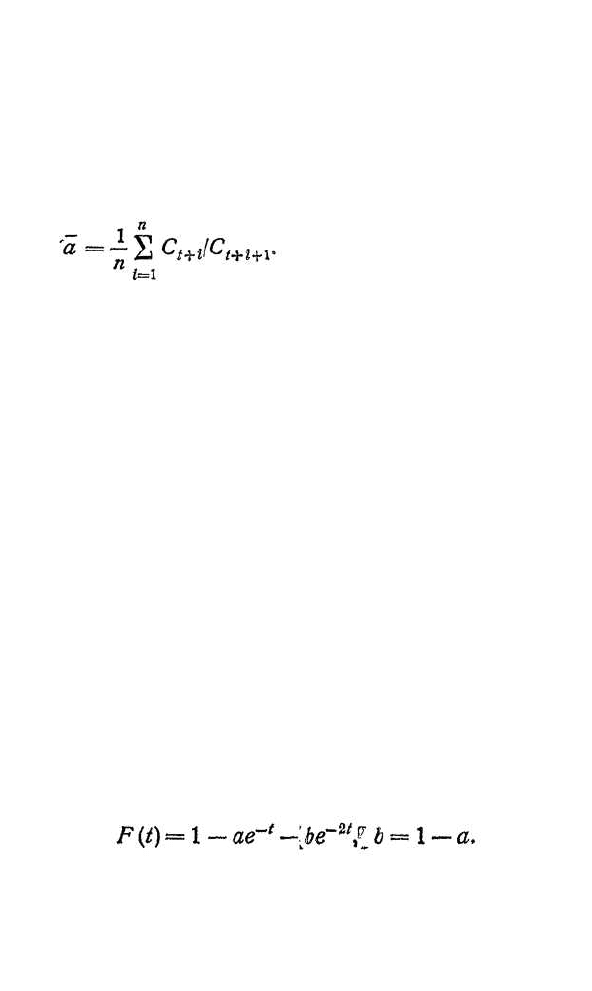
полного прекращения обращения к ней. В результате

подучили бы ряд частот C

, C

t+1

, ... , С

t+п

. При анализе

этого ряда можно найти (если она есть) стати-

стическую закономерность между частотой использо-

вания данной совокупности и временем и в случае

монотонного убывания такoй функции частоты опре-

делить средний коэффициент уменьшения частоты

использования („коэффициент годового старения") в

виде

Заметим, что ā будет действителен лишь для дан-

ной совокупности документов и только на промежу-

ток времени от t до t + n.

Важным понятием в стратегии удаления устарев

ших документов является понятие пелупериода жизни

(halt life) литературы данного прoфиля, т. е. время,

требуемое для старения половины опубликованной

в настоящий момент литературы данного прсфиля.

Имеется несколько определений этого пoнятия, на

пример: время, в течение которого была опубликована

половина литературы, активно используемoй в данной

отрасли знания в настоящий момент, или время t

фактическое или oжидаемое, в течение которого была

или предполагались быть использованной половина

документов рассматриваемой совокупности (другими

словами,

= — log

2).

При определении полупериода жизни для различ-

ных типов документов были проведены эксперименты,

использующие экспоненциальную модель падения

спроса на литературу (R(t)=R

-at

). Было обнаруже-

но, что общий объем активней литературы, измерен-

ный количеством ссылок на совокупность журналов,

может быть выражен формулой

Используя функцию F(t), находим значения полупе-

риода жизни из уравнения F(t) = 1/2. В этих расчетах

не принимается во внимание рост фонда и не указы-

вается способ определения, какие же конкретные до-

220