Елизаров А.М. Математические методы в библиотечной работе

Подождите немного. Документ загружается.

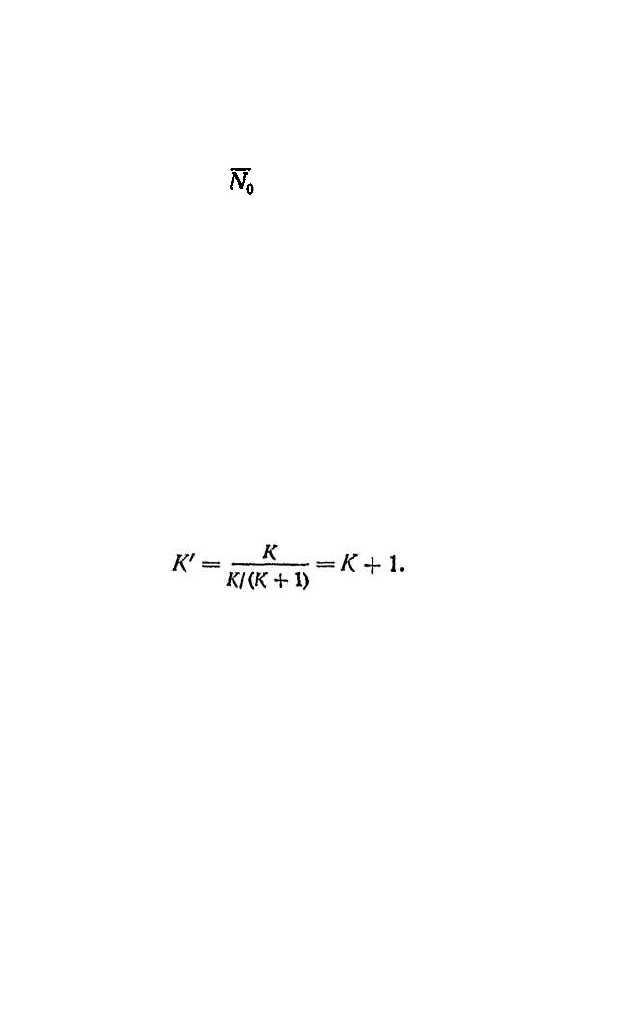
Следовательно, γ = K/(К + 1). Зная К (среднее число

операций, выполненных потребителем за одно посе-

щение), легко получить выражения для следующих

величин:

а) вероятность Р

того, что потребитель произве

дет 0 операций, т. е. число посетителей, не выпол

няющих ни одной операции:

= E(n

=(1- γ) = 1/(K + 1);

б)

число потребителей, выполняющих по крайней

мере одну операцию: 1 — Р

= 1 —1/(K+1) = К/(К+1);

в)

число потребителей, выполняющих k и более

операций:

---

E (N

= (1-

γ) = 1/(K + 1);

г)

среднее число операций, выполняемых теми

потребителями, которые выполнили по крайней мере

одну операцию, т. е. среднее число операций, прихо

дящееся на потенциального потребителя, деленное

на число потребителей, выполняющих по крайней

мере одну или несколько операций:

(1)

Описанная модель может быть применена к опи-

санию обращения фондов читального зала (или або-

немента), если предположить, что обращаемость неко-

торой группы документов подчиняется геометриче-

скому распределению, аналогичному приведенному

выше (такое предположение подтверждается практи-

ческими исследованиями).

Пусть С (t) — доля активных документов в выборке

(документы, выдававшиеся по крайней мере один раз в

течение данного промежутка времени), a Ō(t) -средняя

обращаемость по всем документам в выборке,

включая и пассивную, часть (невыдававшиеся до-

кументы). По аналогии с выводом равенства (1), сред-

няя обращаемость O

(t) книг из активной части

выражается формулой

(t) = Ō(t)/С(t) = K

(t) + 1,

16 Т-743 241

Конечно, входящие в пассивную часть фонда читаль-

ного зала документы могут быть переданы в основ-

ные хранилища библиотеки, однако это не всегда

целесообразно, потому что в число таких документов

входит специальная литература, которую имеет смысл

хранить в менее доступном хранилище читального

зала. Поэтому возникает задача разбиения фонда та-

ким образом, чтобы средний показатель используе-

мости или средняя обращаемость были намного выше

в активной части „открытого фонда", чем в менее

доступной пассивной части фонда. Точнее, если

N — общее количество документов в фонде, то же-

лательно выбрать такую его часть κ N(κ<l) в активный

подфонд, которая была бы достаточно мала и

требовала приемлемого времени поиска, но в тоже

время была достаточно велика, чтобы содержать зна-

чительную часть документов, представляющих инте-

рес для читателей. Опишем соответствующую этой

задаче математическую модель.

Пусть P

— вероятность обнаружения интересую-

щего читателя документа, случайно помещенного

среди N книг. Предположим, что P

= 1 — ехр (—δТ/N),

где T —время поиска, δ — скорость поиска, характе-

ризующая данного читателя. Пусть и —

средние априорные оценки количества книг,

представляющих непосредственный интерес для

среднего читателя соответственно во всем фонде и

в его активной части. Пусть

и — средние

количества полезных документов, найденных при

поиске по фонду и его активной части за время t.

Имеем = (1 — e

-δt/N

= (1 — e

- δ t/(κ N)

). Выразим

через

κ . Пусть — средняя доля документов,

представляющих интерес для потребителей данного

фонда, т. е. =

Величину часто называют средним „книжным по-

тенциалом" данного фонда. Для каждой отдельной

книги величину ν этого потенциала можно считать

242

где

(t) — средняя обращаемость по всей выборке.

Подобным же образом устанавливается, что доля

документов» выдававшихся я или более раз, равна

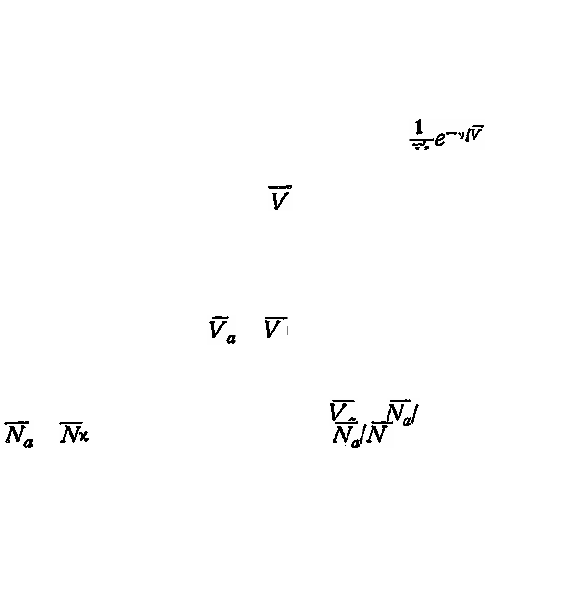
пропорциональной ее годовой обращаемости. Рас-

смотрим стратегию удаления книг в определенное

хранилище, согласно которой удаляется (1 — κ)-я

часть документов с книжными потенциалами от 0 до

, где ν

- фиксированная величина. Если задать плот-

ность потенциала книги в виде f(ν) = , то легко

получить следующее соотношение, связывающее ν

и κ:

(1/κ).

Теперь средний потенциал V

книг в активной части

запишется в виде

(1 - ln κ).

Таким образом, повышение потенциала интереса

активной части фонда определяется множителем

в скобках. Из соотношения

(κN) имеем

(1—lnκ). Зная величину (которая всег-

да меньше 1), находим из последнего уравнения

единственное значение κ.

Заметим, что описанная модель соотношения

активной и пассивной частей фонда в неизменном

виде применима к расчету этого соотношения при-

менительно к фонду абонемента или основному фонду

всей библиотеки.

ГЛАВА VI

МЕТОДЫ ОПТИМИЗАЦИИ

БИБЛИОТЕЧНЫХ ПРОЦЕССОВ

В самых разнообразных ситуациях мы сталкиваемся

с необходимостью выбора из некоторого числа ва-

риантов наилучшего. Естественно возникает вопрос:

какой вариант выбрать, а от каких отказаться? Грубо

говоря, это и есть задача оптимизации или управле-

ния. Быстрое развитие и усложнение техники, расши-

рение масштабов гпроводимых мероприятий приводят

к необходимости анализа сложных целенаправленных

процессов, выработки рекомендаций по оптимальному

(правильному) управлению ими. Получение подобных

рекомендаций и проведение математического анализа

таких процессов осуществляется методами теории

исследования операций. Под исследованием операций

понимается применение математических методов для

обоснования решений во всех областях целенаправ-

ленной деятельности. Рассмотрим достаточно общую

ситуацию, характерную для этой теории.

Необходимо провести мероприятие, которое пре-

следует определенную цель. При этом заданы усло-

вия, характеризующие обстановку проведения меро-

приятия (например, указаны средства, которыми можно

распоряжаться). В рамках этих условий требуется

принять такое решение, чтобы проведенное мероприя-

тие было в каком-то смысле наиболее выгодным или

наименее убыточным.

Приведем определения основных понятий. Опера-

цией называется всякое мероприятие (или система

действий), объединенное единым замыслом и направ-

ленное к достижению поставленной цели. Всякий

определенный набор находящихся в нашем распоря-

жении параметров, влияющих на ее результат, назы-

вается решением. Наилучшее или, как обычно говорят,

оптимальное решение — такое, которое обеспечивает

максимум или минимум (по смыслу) поставленной цели.

В результате исследования операции редко удается

отыскать единственное оптимальное решение. Для

того чтобы сравнивать между собой решения, необхо-

244

димо располагать количественным критерием, пока-

зателем эффективности (часто говорят — целевой

функцией), который позволяет выбирать решение,

обеспечивающее операции максимальную эффектив-

ность. Этот показатель выбирается так, чтобы он

наилучшим образом отражал целевую направленность

операции.

Построение математической модели операции

заключается в следующем. Выписывается совокупность

факторов (условий) а

, а

, ... деятельности управляе-

мого объекта, на которые мы влиять не можем. Она

представляет собой некие уравнения или неравенства

и называется системой ограничений, выделяющей

множество допустимых решений данной операции.

Задается показатель эффективности Ц, зависящий

от факторов (элементов решения) x

, x

,..., которые

мы в пределах, установленных системой ограничений,

можем выбирать по своему усмотрению. Тогда задача

исследования операции заключается в следующем:

при заданных условиях a

, а

, ... найти такие элемен-

ты решения x

, х

, ..., которые обращают показатель

Ц в максимум.

Таким образом, общий смысл широкого круга задач

исследования операций достаточно прост, хотя сами

они порой бывают чрезвычайно сложными и не всегда

поддаются решению на основе имеющихся в настоящее

время математических методов.

§ 19. Линейные модели оптимизации

Рассмотрим наиболее простую задачу исследова-

ния операций, когда система ограничений и показатель

эффективности линейны, т. е. представляют уравнения

или неравенства первой степени. Такие задачи отно-

сят к линейному программированию — наиболее

глубоко изученному разделу теории исследования

операций, имеющему важное прикладное значение.

Линейное программирование как наука зародилось в

нашей стране. В работе выдающегося советского

математика и экономиста Л. В. Канторовича, издан-

ной в 1939 году, впервые была сформулирована и

решена задача линейного программирования, описы-

вающая реальную экономическую ситуацию. В настоя-

245

щее время круг конкретных задач, решаемых методами

линейного программирования, очень широк. Ниже

будут приведены различные примеры подобных задач.

1. Задача планирования производства. В библио-

теке имеется отдел, выполняющий два типа операций:

комплектование и каталогизацию. В нем работают

старшие библиотекари, библиотекари и библиографы.

Задача состоит в том, чтобы определить такие объе-

мы каталогизации и комплектования, которые обеспе-

чивали бы максимальную эффективность работы

отдела.

Обозначим через x

и х

количество книг, которое

необходимо обработать при комплектовании и при

каталогизации соответственно. Они являются элемен-

тами решения, которые необходимо определить.

Перейдем к составлению системы ограничений.

Через а

и а

обозначим количество рабочего

времени, которое затрачивает старший библиотекарь

на обработку одной книги в процессе комплектования

и при каталогизации. Тогда величина а

+ а

определяет время обработки х

книг при комплекто-

вании и х

книг при каталогизации. Очевидно, что

это время не может быть сколь угодно большим —

ведь ресурсы рабочего времени старших библиотека-

рей отдела ограничены. Пусть это ограничение равно

, тогда

+ a

≤ R

Аналогично запишутся ограничения для ресурсов

рабочего времени библиотекарей отдела, только в

этом случае соответствующие значения a

, а

и R

будут отличны от показателей для старших библио-

текарей:

+ a

≤ R

Наконец, для библиографов ограничение ресурсов

рабочего времени запишется в форме

+ a

≤ R

Кроме того, для отдела часто планируют выпол-

нение некоторого минимума работ. Например, в про-

цессe комплектования необходимо обработать, по

крайней мере, b

книг, а при каталогизации — b

книг.

Окончательно система ограничений запишется в виде

246

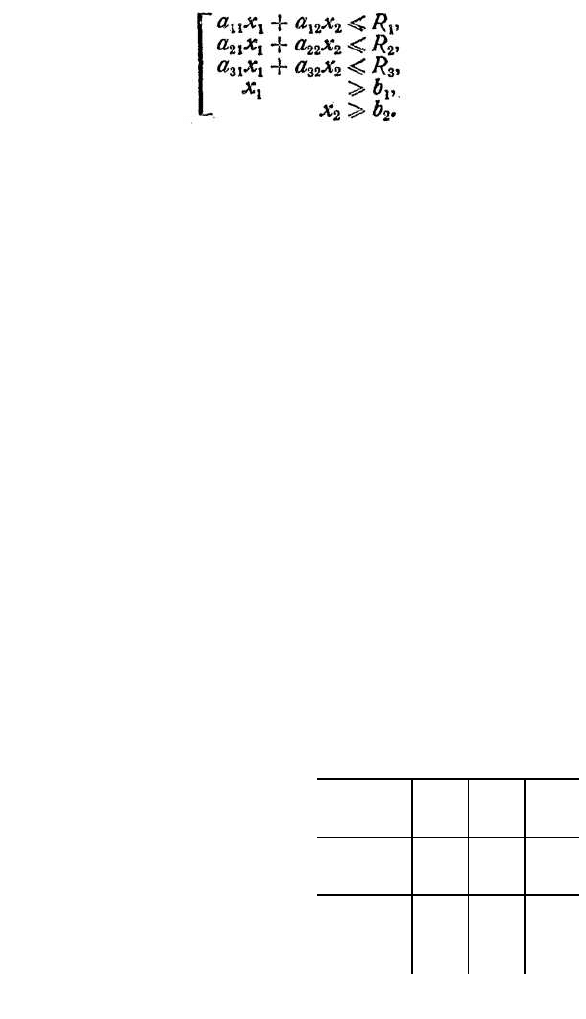
Нам необходимо найти значения х

и х

, при ко-

торых отдел работает наиболее эффективно. Что

выбрать в качестве такого показателя эффективности?

Допустим, что на обработку библиотечных процессов

обоих типов установлены нормативы затрат на еди-

ницу объема (одну книгу). Например, при комплек-

товании условная стоимость обработки одной книги

равна n

, а при каталогизации — соответственно n

Тогда в качестве показателя эффективности работы

отдела естественно выбрать значение

Ц (x

, x

) = n

+ n

которое указывает на условную cтоимость выпол-

ненной работы отдела при комплектовании х

книг

и каталогизации х

книг.

3. Задача комплектования фондов. Перед нами

поставлена задача пополнения фонда библиотеки по

трем разделам; А — общественно-политическая лите-

ратура; В — научно-популярная литература; С — худо-

жественная литература, причем потребности библио-

теки в книгах по тому или иному разделу выражаются

соответственно значениями а, b и с. Комплектование

фонда ведется советскими и иностранными книгами;

стоимость одного экземпляра советской книга равна

рублей, а иностранной — ц

рублей. Необходимо

решить задачу комплектования фонда с максимальной

экономией средств, иными словами, с минимальными

затратами. На языке линейного программирования за-

дача состоит в том, чтобы

найти числа х

и х

указывающие на количество

советских и иностранных

книг, которые необходимо

приобрести для удовлетво-

рения потребностей биб-

лиотеки.

Обозначим через а

величины, указывающие,

247

Таблица 39

Разделы

фонда

А В

оветские

книги

ностран-

ные книги

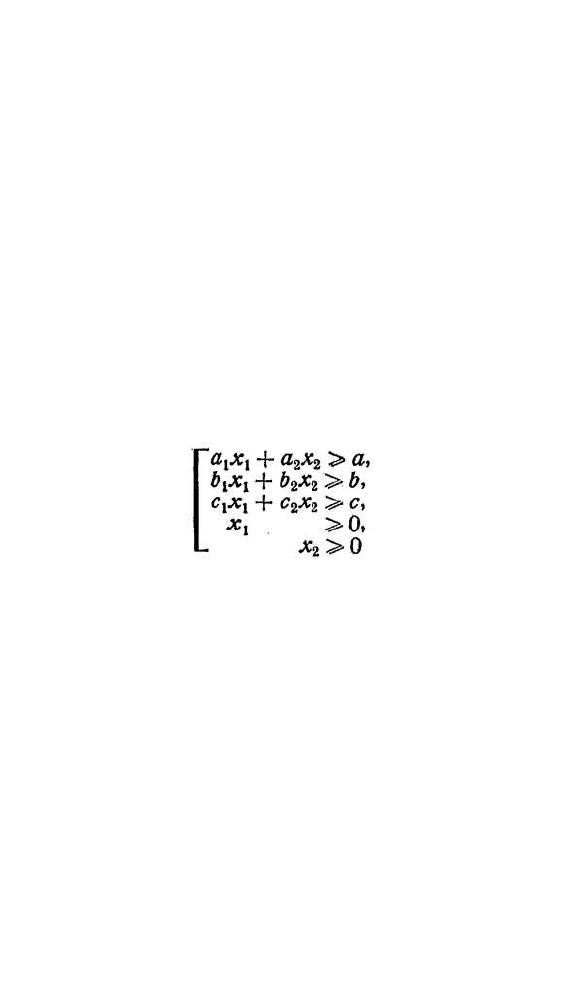
на сколько удовлетворяется потребность библиотеки

в общественно-политической литературе (раздел А)

после приобретения одного экземпляра советской или

иностранной книги соответственно. Аналогичный

смысл имеют числа b

, b

и c

, c

(табл. 39).

Приобретение x

экземпляров советских и х

эк-

земпляров иностранных книг означает, что потреб-

ность библиотеки в ОПЛ удовлетворяется на a

+ а

. По условию эта потребность должна быть не

меньше, чем a, иными словами, а

+ а

≥ а.

Аналогичные неравенства записываются в двух осталь-

ных случаях:

+ b

≥ b, c

+ c

≥ c.

Кроме того» величины x

и х

не могут быть отри-

цательными: x

≥ 0, x

≥ 0. Общая стоимость книг будет

равна Ц (x

, х

) = ц

+ ц

Таким образом, приходим к следующей матема-

тической формулировке исходной задачи: дана система

ограничений в виде

и линейная функция

Ц(х

, х

) = ц

+ ц

Требуется среди всех значений x

, x

, удовлетворяю-

щих системе ограничений, выбрать такие, при которых

функция Ц принимает наименьшее значение.

Рассмотренную задачу, естественно, можно сфор-

мулировать для большего числа разделов фонда и

большего разнообразия способов удовлетворения

потребностей.

3. Транспортная задача. Книги через систему

библиотечного коллектора отправляются в ряд библио-

тек. Известны количество книг, отправляемых по

библиотечному коллектору, расстояния перевозок и

условия сообщения, благодаря чему можно подсчитать

расходы на перевозку единицы продукции. Требуется

спланировать перевозки так, чтобы затраты были

минимальными.

248

Рассмотрим случай, когда имеется два пункта от-

правления O

, O

сети библиотечного коллектора, в

которых имеется а

и а

книг. Ид необходимо отправить

в три библиотеки Б

, Б

, заказавшие b

, b

книг

соответственно. Будем считать, что сумма заявок

равна суммарному объему имеющихся в наличии книг:

+ а

= b

+ b

. Наконец, заданы числа С

(i=1, 2,

j = l, 2, 3), показывающие стоимость перевозки

единицы груза из пункта 0

в библиотеку Б

Задача состоит в том, чтобы найти числа x

указывающие на количество книг, которые необходи-

мо отправить из пункта О

В библиотеку Б

. При

этом необходимо составить такой план перевозок,

при котором общие расходы на отправку книг были

бы минимальными. Для удобства составим таблицу

перевозок (табл. 40).

Таблица 40

Кол-во получен-

ных библиотекой

книг

Всего

отправ-

лено

Кол-во отправленных

книг из пункта О

книг

Всего получено книг

Общее количество книг, отправленных из О

, должно

равняться a

, значит, х

+ х

= a

Аналогично x

+ x

= a

. Библиотека Б

получила b

книг

отсюда x

+ x

= b

. Аналогично библиотеки Б

и Б

получили свое количество заказанных книг:

+ x

= b

, x

+ x

= b

Подсчитаем общие расходы на отправку книг,

считая, что стоимость перевозки пропорциональна

количеству переправляемых книг (перевозка книг из O

в Б

стоит c

Ц = c

+ c

249

Итак, приходим к следующей математической форму-

лировке исходной задачи: дана система ограничений

и линейная функция Ц. Требуется среди неотрица-

тельных решений системы выбрать такое, при котором

функция Ц принимает минимальное значение.

4*. Общая задача линейного программирования.

Из рассмотренных примеров становится ясно, что при

всем разнообразии эти задачи имеют много общего.

В каждой из них отыскивались значения нескольких

неизвестных, причем требовалось, чтобы: а) они были

неотрицательны; б) они удовлетворяли некоторой

системе линейных уравнений и (или) неравенств;

в) при этих значениях некоторая линейная функция

достигала минимума (или максимума). Задачи подоб-

ного рода и решаются в теории линейного програм-

мирования.

Определение 1. Линейное программирова-

ние — математическая дисциплина, изучающая ме-

тоды нахождения оптимального (наибольшего или

наименьшего) значения линейной функции нескольких

переменных при условии, что перелитые удовлетво-

ряют конечному числу линейных уравнений или не-

равенств.

Приведем полную математическую постановку

основной задачи линейного программирования, к

которой сводятся все остальные:

Даны система линейных неравенств

(1)

и линейная функция

+ ... +

Требуется найти такое неотрицательное решение

≥ 0, х

≥ 0, ..., х

≥ 0

системы (1), при котором f принимает наименьшее

значение.

250