Елизаров А.М. Математические методы в библиотечной работе

Подождите немного. Документ загружается.

Данные о читаемости (последняя колонка табли-

цы 22) приведены в виде ряда чисел в табл. 23.

Таблица 23

Читатель Ч

ξ = число

книг

19 16 20

21 17 20 18 15

Как правило, цифровая информация в виде ряда

мало пригодна для непосредственного изучения

(представим, что в библиотеке 1000 читателей).

Такой ряд представляет собой первичную форму

записи статистического материала и подлежит даль-

нейшей обработке. Наиболее простой и распростра-

ненный способ упорядочения — это ранжирование,

т. е. расположение значений случайной величины ξ в

порядке их возрастания или убывания.

Пример 2. В результате ранжирования ряда чи-

сел из таблицы 23 получается ранжированный ряд

(табл. 24).

Таблица 24

Ранг

2 3 4 5 6 6 7 8

ξ 15 15 16 17 18 19 20 21 22 26

В некоторых случаях ранжирование оказывается

достаточным для получения содержательных выводов.

Например, ранжирование периодических изданий по

годовому количеству публикаций по определенной

теме позволяет судить о рассеянии информации и

организовать подписку на наиболее продуктивные

журналы. Однако ранжирование перестает быть на-

глядным при большом числе вариантов в выборке

и чаще всего используется как вспомогательный прием

перед другими видами упорядочения.

Одним из таких видов упорядочения является

дискретная группировка, заключающаяся в распре-

делении совокупности вариантов по грушам, содер-

жащим одинаковые варианты. Получающийся при этом

ряд становится более обозримым, чем ранжированный.

121

Пример 3. В результате группировки данных

таблицы 24 получаем ряд» представленный табли-

цей 25.

Таблица 25

Количество читателей 2 1 1

1 2 1 1

ξ = количество книг 15 16 17 18 19 20 21 26

Определение 1. Число п

, показывающее, сколько

раз некоторый вариант х

встречается в выборке х

..., x

, называется чистотой данного варианта.

Ясно, что сумма всех частот равна объему выбор-

ки: п

= k.

Отметим, что дискретная группировка позволяет

обработать данные об атрибутивной вариации при-

знака без предварительного ранжирования, невозмож-

ного для качественных признаков.

Пример 4. Распределение читателей мини-биб-

лиотеки по профессии и образованию представляется

таблицами 26 и 27.

Таблица 26

Слесарь Оператор

Сварщик Инженер

4 2 2

Таблица 27

Однако частота не позволяет сравнивать совокуп-

ности разного объема (из равенства частот еще не

будет следовать, что вариант встречается одинаково

часто для обеих совокупностей, т. к. их объем может

быть различен). Для удобства сопоставления в стати-

стике вводятся относительные величины.

Определение 2. Относительной частотой ω

некоторого варианта х

называется доля этoго

122

Имеет среднее образование Имеет высшее образование

варианта среди всех вариантов выборка, т. е.

= n

/ ∑ n

Относительную частоту также назы-

вают частостью.

Для удобства относительную частоту выражают

в процентах, умножая ω

на 100%.

Определение 3. Дискретным вариационным

рядом называется таблица, составленная из значений

варьируемого признака (вариантов) и соответ-

ствующих им числовых характеристик.

Пример 5. Построим дискретные вариационные

ряды для распределения совокупности читателей мини-

библиотеки по читаемости (таблица 28).

Таблица 28

i 1

6 7

16 17 18 19

20 21 26

0,2

0,1

0,2

0,1

Часто собранный материал всё же очень обширен,

и дискретный вариационный ряд получается громозд-

ким. В этом случае для упорядочения статистических

данных используется способ интервальной группи-

ровки: область вариации значений признака разбива-

ется на некоторое число интервалов и подсчитывается

число вариантов, попавших в каждый интервал. Поня-

тия частоты и относительной частоты определяются,

как и при дискретной группировке, но относятся теперь

не к отдельному варианту, а ко всему интервалу.

Пример 6. В таблице 29 представлен результат

интервальной группировки данных из таблицы 22.

Таблица 29

Читаемость

(интервал

для x

)

15-17,75

17,75—20,5 20,5—23,25

23,25—26

Частота n

(чис-

ло читателей)

4 4 1

Относительная

частота

0,4 0,4 0,1

0,1

123

При составлении таблицы мы разбили область изме-

нения ξ (от 15 до 26 книг) на четыре равных интер-

вала и подсчитали частоты и относительные частоты

вариантов, попавших в каждый из интервалов.

Определение 4. Интервальный вариацион-

ный ряд — это ряд, полученный в результате интер-

вальной группировки.

Примерами таких рядов могут служить строки

из таблицы 29.

Максимальнее значение варианта из заданного

интервала называется верхней границей Xj

max

, а

минимальное—нижней границей Xj

тiп

интервала, h

max

- Xj

тiп

называется величиной интервала.

Например, в вариационных рядах из таблицы 29:

тiп

= 15, X1

таx

=17,75, h

=2,75.

Построение интервального вариационного ряда

осуществляется следующим образом: выбирается ниж-

няя граница первого интервала х

1тin

так, чтобы

1тin

= х

тin

- h/2, затем строятся интервалы длины h до

тех пор, пока начало очередного интервала не

окажется равным или большим х

таx

3. Графическое представление. Для наглядности

рассмотрения статистических данных вариационные

ряды изображают графически. Наиболее часто исполь-

зуют полигон распределений и гистограмму.

Определение 1. Полигон — графическое изобра-

жение дискретного вариационного ряда в прямо-

угольной системе координат, когда величины признака

откладываются по оси абсцисс, частоты (или отно-

сительные частоты) — по оси ординат и полученные

точки соединяются отрезками.

Полигон применяется преимущественно для пред-

ставления дискретных рядов с небольшим числом

вариантов.

Пример 1. Построим полигон частот для дискрет-

ного вариационного ряда, представленного табли-

цей 25 из п. 2. Для этого по оси Ох отложим значения

а по оси Оу—соответствующие им частоты. Затем

соединим полученные точки отрезками (рис. 52).

Определение 2. Гистограмма — графическое

изображение интервального вариационного рядa

в виде прямоуголъников, основания которых coвпа-

дают с интервалами изменения признака, а высоты

124

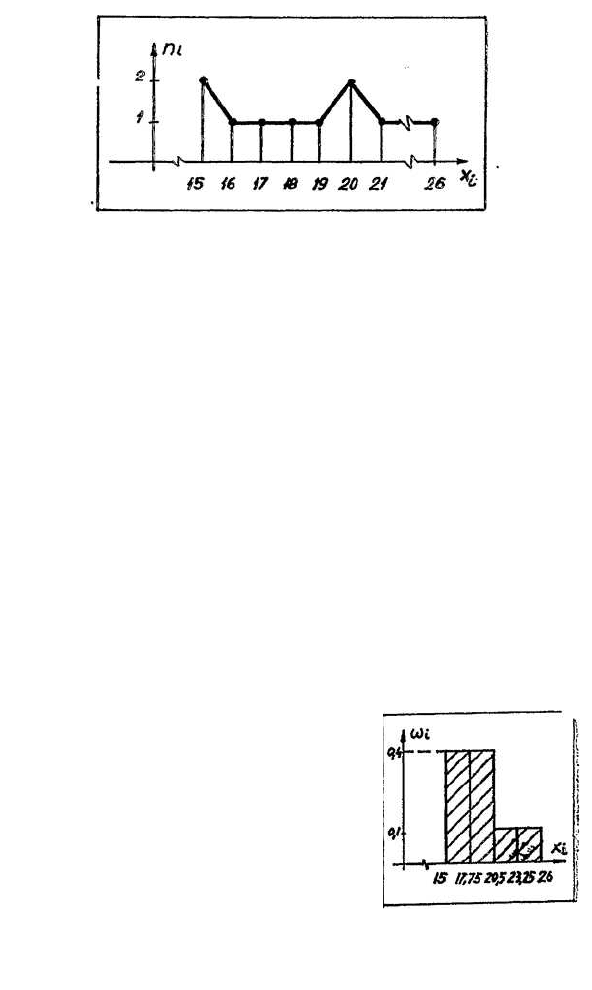
Рис. 52. Полигон частот

пропорциональны частотам (или относительным

частотам) вариантов, попавших в соответствующие

интервалы.

Гистограмма строится таким образом, что площадь

всех прямоугольников оказывается равной числу всех

наблюдаемых вариантов (т. е. объему совокупности)

или равной 1 в зависимости от того, что мы строим—

гистограмму частот или относительных частот.

Пример 2. Построим гистограмму относительных

частот для интервального вариационного ряда из

таблицы 29 п. 2. Имеем h = 2,75. Над каждым интер-

валом строим прямоугольник следующей высоты:

определяем все варианты, попавшие в интервал; скла-

дываем все их относительные частоты; делим их на

величину h; получившееся число и есть требуемая

высота. Площадь построенного таким образом прямо-

угольника равна сумме относительных частот, попав-

ших в интервал (рис. 53).

Укажем практические приемы построения таблицы

определяющей интервальный ряд. Выбирают интер-

валы (как привило, не более 20)

и в верхней строке указывают их

границы; затем просматривают под-

ряд все варианты и во второй

строке делают отметки против

соответствующего интервала, если

очередной вариант попал в указан-

ные границы. Эти отметки полезно

группировать, используя следую-

щую символику. Первые четыре

варианта отмечают точками - вер- Рис. 53. гистограмма

шинами квадрата, следующие че- относительных частот

125

тыре варианта отмечают отрезками—сторонами квад-

рата, девятый и десятый варианты — диагоналями.

Получается

Следующий десяток отмечается

вторым квадратом и т. д.

Лучше всего длины интервалов брать одинаковы

ми. Это облегчает построение гистограмм и дает

наглядную картину. Однако иногда оказывается, что

в несколько интервалов попадает основное количество

вариантов. Гистограмма в этой части может неправиль-

но отражать распределение частот, сглаживать подоб-

ные всплески и „размазывать" их на весь интервал.

В этом случае полезно разбить интервалы на более

мелкие. Если взять очень большое количество интер-

валов малой длины, то число вариантов, попавших

в каждый интервал, будет невелико и изменение

высот ступенек не даст правильного представления

о вариационном ряде. Поэтому число интервалов

выбирают исходя из характерных особенностей того

или иного ряда. Эмпирическим путем установлено,

что оптимальную величину интервалов ряда h

опт

можно расчитывать по формуле h

oпт

=(x

max

— x

min

)/l,

где х

тax

и х

min

— значения

Таблица 30 самого большого и самого

маленького вариантов со-

вокупности, k — объем cово-

купности. Число же интер-

валов определяется из

выражения l ≈ 1 + 3,3 1gk

(с округлением до большего

целого) или из эмпирических

наблюдений, приведенных в

таблице 30.

§ 12. Статистические характеристики

случайных величин

Пусть на генеральной совэкуцносш задана, слу-

чайная величина ξ (дискретная или непрарывная), при-

нимающая на объектах совокупности числовые значе-

ния. Осуществив выборку, мы цолучаем ряд чисел

, ... , x

. По этим числам нужно охарактеризоватьξ,

т. e. приближенно описать, ее закон распределения,

математическое ожидание, дисперсию и т. д. Что вы-

126

исло

интервалов, l

Объем, k

—

6—8

7—10

8—12

15—20

—

40-60

60—100

100—200

более 200

бирается в качестве таких статистических эквивален-

тов —об этом и пойдет речь в настоящем параграфе.

Вопросы о степени соответствия вводимых характе-

ристик мы отложим до следующего раздела.

1. Статистический закон распределения. Наблю-

даемые в эксперименте значения x

сами представляют

случайные величины (лишь от случая зависит, что

в качестве i-го значения было зафиксировано именно

число x

, а не какое-нибудь другое значение ξ). По-

этому событие ξ = x

является случайным и связано с

соответствующей выборкой х

, х

, ... , x

из генеральной

совокупности. При определенных условиях (ниже мы

укажем, каких) на эту выборку можно смотреть, как на

k независимых опытов, в результате которых происходят

события типа ξ = x

. При этом вероятность появления

этого события (кaк мы отмечали в п. 1 § 9)

приближенно характеризуется частотой появления

варианта x

среди элементов выборки. Приведем здесь

для полноты это определение.

Определение 1. Статистической вероят-

ностью события А (обозначается Р*(А)) в серии

из k опытов называется отношение числа опытов

в которых это событие произошло, к общему числу

произведенных опытов.

Иными словами» для события ξ = х

статистическая

вероятность Р* (ξ = x

) = ω

есть просто относительная

частота ω

варианта x

. Простейшей формой закона

распределения был ряд распределения, задаваемый

таблицей пар значений (ξ, P) (см., п. 1§9). Статисти-

ческим аналогом этого закона будет, естественно,

таблица из выборочных значений случайной величи-

ны x

и статистических вероятностей Р* (ξ = x

) = ω

их

появления, т. е. статистический закон распределения

случайной величины ξ представляет дискретный

вариационный ряд относительных частот. Следова-

тельно, статистическим многоугольником распреде-

лений является полигон относительных частот. Дру-

гой способ графического представления статистиче-

ского закона распределения связан с построением,

гистограммы (см. п. 3 из § 11).

Остановимся на определении статистической функ-

ции распределения.

127

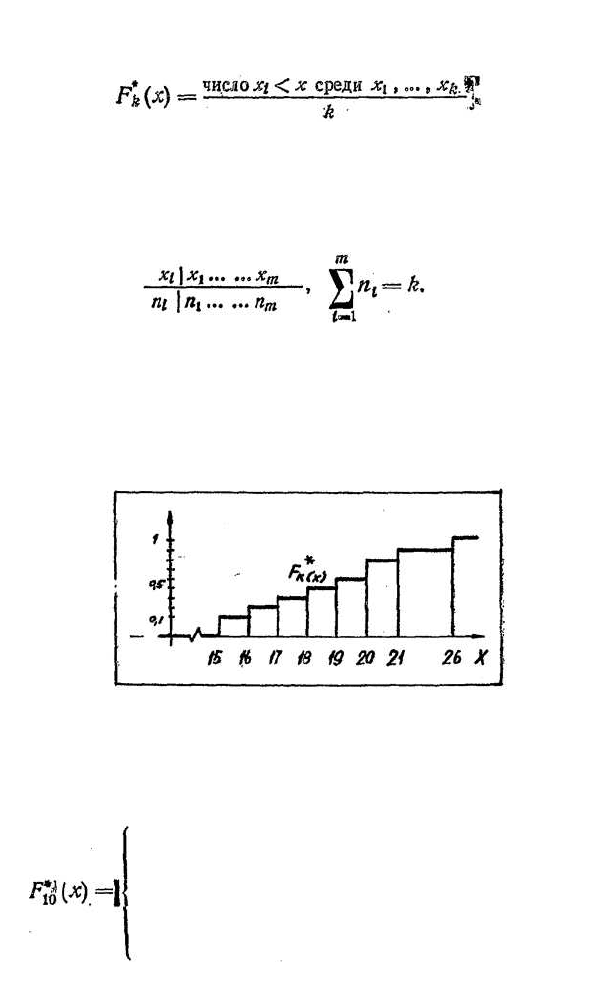
Определение 2. Статистической (элпшри-

ческой или выборочной) функцией распределения

случайной велтини ξ называют функцию

Она зависит от случайных значений x

, ... , x

, реа-

лизовавшихся в k экспериментах, и, следовательно,

сама является случайной функцией. Укажем способ

ее построения. Пусть задан дискретный вариацион-

ный ряд

Каждому значению х

припишем число 1/k. Для всех

х<х

полагаем F*

(x)=0. Если х

≤х<х

, то F*

(x)=

/k = Р* (ξ < х

). С переходом через очередное зна-

чение х

к значению F*

добавляется n

/k = Р* (ξ = x

Пример 1. Построим статистическую функцию

распределения для вариационного ряда из таблицы 23

Рис. 54

(см. п. 2 § 11). График функции F*

(x) - ступенчатая

линия со скачками n

/k (рис. 54). Поэтому она задается

соотношениями

128

О при

< 15, 6/10 при 19≤x<20,

2/10 при 15≤х<16, 8/10 при 20≤x<21,

3/10 при 16≤x<17, 9/10 при 21≤x<26,

4/10 при 17≤x<18, 1 при х≥26.

5/10 при 18≤x<19,

Имея график F*

(x), можно приблизительно указать,

как ведет себя (теоретическая) функция распределе-

ния случайной величины.

Для построения статистического аналога понятия

плотности вероятности применяется интервальный

вариационный ряд, в котором область изменения зна-

чений признака (вариантов) разбивается на интервалы

=(x

, х

) и ω

подсчитываются для всех вариан-

min max

тов x

, попавших в соответствующий интервал I

Определение 3. Статистической плот-

ностью вероятности называется функция

где х

, х

— начало и конец интервала I

, a h

—

mln max

его длина.

Она представляет кусочно-постоянную ступенча-

тую функцию. График р*(х) есть не что иное, как

гистограмма относительных частот данного ряда. Ею

мы по сути дела уже пользовались при интуитивном

обосновании понятия плотности вероятности в рас-

суждениях п. 2 § 9.

2. Меры центральной тенденции. Для более пол-

ного анализа статистических данных используют ха-

рактеристики, определяющие основную тенденцию

признака, некоторое среднее, типичное, значение при-

знака, вокруг которого группируются остальные вари-

анты. Эти меры являются аналогами понятия матема-

тического ожидания случайной величины. К ним

относятся статистическое (или эмпирическое) матема-

тическое ожидание, мода и медиана.

Пусть в результате статистического эксперимента

из генеральной совокупности значений случайной

величины ξ была осуществлена выборка х

, х

,..., x

Определение 1. Статистическим (или выбо-

'очным) математическим ожиданием называется

число =Е*ξ=

Если в совокупности произведена диокретная груп-

пировка, например, если задан статистический закон

распределения ξ, то вместо нахождения среднего ариф-

9 Т-743 129

метического всех вариантов, Е*ξ можно вычислять

по формуле Е*ξ= x

Пример 1. Найдем Е*ξ для выборки, заданной

таблицей 28 из п. 2 § 11 (табл. 31).

Таблица 31

Заметим, что по указанной формуле можно про-

извести упрощенное вычисление Е*ξ для интерваль-

ного вариационного ряда. В этом случае принимается,

что значения признака внутри интервала равны полу-

сумме верхней и нижней границ интервала (это число

называют центром интервала), которую берут в каче-

стве вариантов в формуле.

Непосредственным следствием отмеченной фор-

мулы является формула вычисления Е*ξ по относи-

тельным частотам или статистическим вероятностями

Е*ξ=

•ω

= x

P*(ξ = x

Статистическое математическое ожидание является

в некотором смысле условной величиной, ибо в сово-

купности может не быть ни одного объекта с найден-

ным ожиданием (см. пример 1). Так, при определении

средней посещаемости библиотеки могут получиться

дробные числа (дробное число посещений?), которые

приближенно отражают посещаемость библиотеки.

В некоторых случаях вместо математического ожида-

ния используют так называемые непараметрические

средние — моду и медиану.

Определение 2. Модой называется значение

варианта, имеющее наибольшую частоту (обознача-

ется Мо ξ).

На полигоне частот Мо ξ — самая высокая вершина.

Если полигон имеет более одного максимума, то

130

15 18

20 26

1 1

1 1 12 2

Здесь