Елизаров А.М. Математические методы в библиотечной работе

Подождите немного. Документ загружается.

распределение называется многомодальным. Напри-

мер, распределение из примера 1 п. 3 § 11 многомо

дально.

Мода — единственная мера центральной тенденции,

которой может быть охарактеризована совокупность

с качественной вариацией признака. Например, для

распределения из таблицы 26 (п. 2 § 11) модальной

является профессия оператора.

Укажем способы отыскания моды в тех случаях,

когда статистические данные заданы не в виде дис-

кретного вариационного ряда частот. Если информа-

ция представлена ранжированным рядом и два сосед-

них варианта имеют одинаковую частоту, превышаю-

щую все остальные частоты, модой считают полусумму

этих вариантов. В интервальном вариационном ряде

расчитывают условное значение моды по формуле

Мо ξ = x

Моmin

+ h

(п

-n

Mo-1

)/(2n

- п

Mo-1

-n

Mo+1

где x

Mo min

—начало модального интервала, h

и n

—

величина и частота модального интервала, n

Mo-1

—ча-

стота интервала, предшествующего модальному,

Mo+1

- частота интервала, следующего за модальным.

Определение 3. Медианой называется значе-

ние варианта, делящее ранжированный ряд пополам

(обозначается Me ξ).

Геометрический смысл медианы прост — это абс-

цисса точки, в которой площадь гистограммы делится

пополам. Ее еще можно определить соотношением

Р *(ξ< М e ξ)=Р *(ξ>М e ξ).

Укажем способы вычисления медианы. Если стати-

стические данные заданы дискретным вариационным

рядом с нечетным числом вариантов, то Me ξ—вариант

с номером (k + 1)/2. Если же число вариантов четно,

то в качестве Meξ берут полусумму вариантов х

k/2

k/2+1.

Пример 2. Найдем медиану для выборки, пред-

ставленной таблицей 24 из п. 2 § 11: число вариантов

четно, поэтому Meξ = (x

+ х

)/2 = 18,5. В интервальном

вариационном ряду рассчитывается условное

значение медианы по формуле

ξ = x

Me min

+ h

(1/2

∑

- N

Me-1

)/n

9* 131

где x

Ме min

—начало медианного интервала I

Ме

, т. е.

интервала, которому соответствует первая частота,

прибавление которой к сумме частот всех предыдущих

интервалов становится больше половины объема вы-

борки (т. е. n

); n

, h

— частота и величина

медианного интервала; N

Me-1

— сумма частот для всех

предшествующих интервалов.

При использовании той или иной меры централь-

ной тенденции в практических исследованиях необ-

ходимо учитывать, в каких случаях применение этой

меры сопровождается наименьшим числом ошибок.

На моду и медиану величины вариантов с небольшой

частотой не влияют. Как правило, крайние значения

совокупности больше всего склонны к неустойчивости

и имеют наибольшую частоту. С другой стороны, на

величину математического ожидания влияют все вари-

анты. Эти соображения определяют целесообразность

использования моды и медианы при наличии в сово-

купности значений, резко отличающихся от остальных,

но имеющих малую частоту. В небольших совокуп-

ностях мода может быть нестабильной и поэтому

непригодной для оценки. Здесь нужно использовать

медиану или математическое ожидание.

Мода обычно применяется в тех случаяx, когда

варианты, тесно сгруппированы в центре ряда. Медиана

дает большее число ошибок, но зато величина каждой

ошибки в этом случае минимальна. Если сведения об

изучаемом явления неполны и точны лишь для вари-

антов, расположенных в центре ряда, то целесообраз-

нее всего использовать медиану.

Математическое ожидание характеризуется тем,

что при его вычислении оказываются наименьшими

квадраты ошибок. Этим объясняется его широкое

применение в статистике.

3. Меры изменчивости. Меры центральной тенден-

ции характеризуют совокупность с точки зрения одно-

родности ее элементов. Но именно различия элемен-

тов вызывают необходимость их статистической обра-

ботки. В исследованиях вводятся меры, оценивающие

вариацию (разброс) признаков. Основными из них

являются: а) статистическая (или эмпирическая) дис-

персия; б) среднее квадратичное отклонение; в) вариа-

ционный размах; г) среднее линейное отклонение.

132

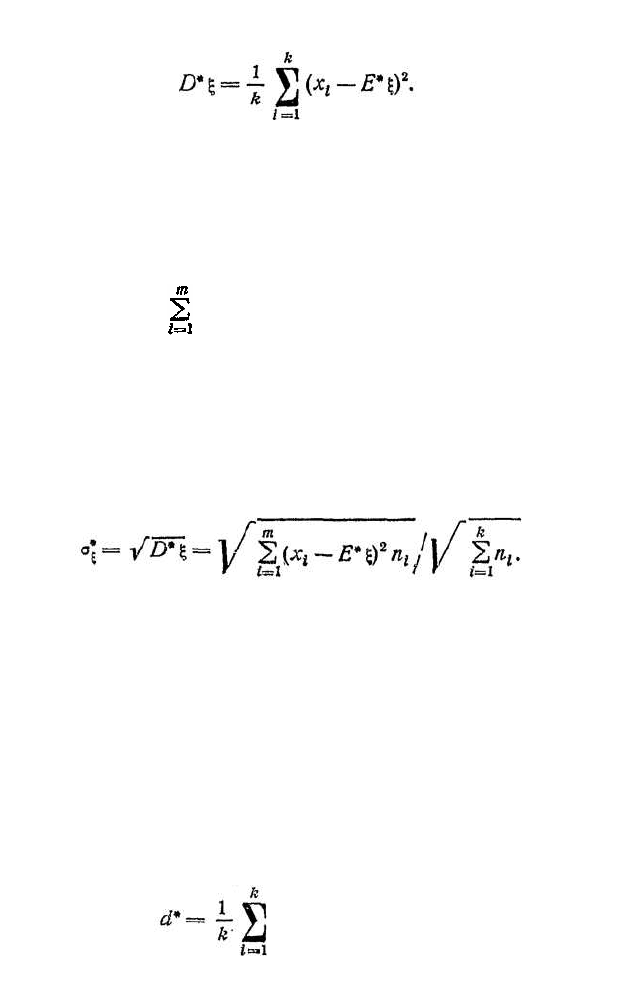
Определение 1. Статистической (или вы-

борочной) дисперсией называется число

Иногда D*ξ обозначают s

или σ

Это число указывает, на сколько в среднем вари-

анты отклоняются от центра (статистического мате-

матического ожидания).

Если статистические данные представлены в виде

дискретного вариационного ряда относительных ча-

стот, то статистическая дисперсия вычисляется по

формуле D*ξ = (x

— Е* ξ)

• ω

, которая получается

из определения D*ξ группировкой одинаковых слагае-

мых. С помощью этой формулы дисперсию можно

вычислять и для интервальных вариационных рядов,

если в качестве вариантов x

выбрать значения центров

интервалов.

Для того чтобы выразить меру рассеяния в тех

же единицах измерения, что и значения признака,

используют среднее квадратичное отклонение

Простейшим показателем, характеризующим разно-

образие изучаемой совокупности, является вариацион-

ный размах r* = x

тax

— х

тiп

. Как мода и медиана,

вариационный размах не учитывает всех значений

признака в совокупности. Он зависит лишь от край-

них вариантов и дает весьма грубую оценку вариации

признака. Используется г* лишь для приближенной

характеристики. Более надежным показателем является

среднее линейное отклонение.

Определение 2. Средним линейным отклоне-

нием навивается среднее арифметическое абсолют-

ныл величин отклонений вариантов от их стати-

стического математического ожидания, т. е.

-E*ξ|.

133

Поскольку d* учитывает величину всех вариантов,

характеристика получается более объективной. Отме-

тим, что если в качестве меры центральной тенденции

используется математическое ожидание, то дисперсия

в роли показателя вариации предпочтительнее. На-

оборот, если центральная тенденция измеряется при

помощи медианы, то в качестве меры изменчивости

следует использовать линейное отклонение. Оценку

представительности меры центральной тенденции мож-

но произвести не только в абсолютных единицах, но

и с помощью относительных величин, называемых

коэффициентами вариации.

Определение 3. Коэффициентом вариации V

называется отношение меры изменчивости к мере

центральной тенденции.

Как правило, это отношение выражается в про-

центах. Наиболее распространены следующие коэф-

фициенты:

— по вариационному размаху V

= 100% r*/E*ξ;

— по среднему линейному отклонению

=100%•d*/E* ξ;

— по среднему квадратичному отклонению

V σ,= 100% σ*/E*ξ.

§ 13. Выборочный метод исследования

Суть выборочного метода заключается в изучении

генеральной совокупности по части ее объектов,

называемой выборкой. К подобному методу исследо-

вания мы обращаемся тогда, когда интересующая

нас совокупность слишком многочисленна или ее

объекты труднодоступны. Отбор выборки желательно

осуществить так, чтобы она наилучшим образом пред-

ставляла целое, была репрезентативной. Для мало

или совсем неизученной генеральной совокупности

лучшее, что можно предложить, — это случайный

выбор. При этом возникает ряд случайных величин,

которые необходимо соотнести с исходной совокуп-

ностью и описать надлежащим образом то явление,

которое подвергается исследованию. В математической

статистике созданы несколько математических моде-

лей, описывающих способы статистической обработки,

с которыми мы познакомимся в этом параграфе.

134

1. Выборка. Начнем с обсуждения вопросов о по-

строении математической модели, достаточно верно

отражающей статистическую обработку данных экспе-

римента.

Пусть мы имеем ряд наблюдений х

, х

,...,х

которые представляют собой случайные величины.

Имеются две возможности: либо эти случайные вели-

чины распределены одинаково (имеют один и тот же

закон распределения), либо по-разному. Вторая воз-

можность выглядит более общей, однако, начав ее

моделировать, мы сразу же сталкиваемся с непреодо-

лимыми трудностями. Действительно, предположим,

что указанный ряд наблюдений получен в результате

длительного (многолетнего) исследования посещае-

мости ξ библиотеки и х

дают число посетителей

в один из месяцев того или иного года. Если мы

хотим спрогнозировать среднюю посещаемость (будем

описывать ее с помощью Ех

), то при условии отсут-

ствия связей между х

, ... , х

мы ничего не сможем

сказать о величине Ех

в зависимости от Ех

, ..., Ех

k-1

С другой стороны» более частная модель» когда

предполагают, что х

,...,х

распределены одинаково,

позволяет дать приближенную оценку для Ех

, выбрав

для этого Ех

≈ (x

+ ... + x

k-1

)/(k — 1) = Е* ξ. Сразу

же заметим, что указанная модель может неправильно

отражать изучаемое явление. Например, из-за расши-

рения библиотеки посещаемость ир года в год могла

расти: Ех

< Ех

< ... < Ех

k-1

< Ех

. Но мы в качестве

Ех

выбрали величину Е*ξ и, тем самым, занизили прогноз

посещаемости библиотеки на будущий год. Итак, при

построении статистической модели необходимо

выбирать между общей моделью (бесполезной из-за

невозможности определить ее параметры) и частной

(которая может быть неверной и привести к не-

правильным выводам). Поэтому использование того

или иного допущения, в частности, о равнораспре-

деленности ряда наблюдений х

, ..., х

должно быть

тщательно проверено. Допустим, что х

— одинаково

распределенные случайные величины. Но этого пред-

положения мало, чтобы делать выводы о значении Ех

ибо нам важно знать величину ошибки в приближен-

ном равенстве Ех

≈ E*ξ. Для этого нужно вычислить

дисперсию величины E*ξ, т.е. D[(x

+ ... +x

)/(k —

-1)]= D (х

+ ... + x

k-1

)/(k — 1)

. Однако в случае зависи-

135

мых случайных величин х

, ... , х

мы ничего не

сможем сказать о дисперсии, суммы—она зависит от

степени зависимости (корреляции) х

i .

и x

. Лишь в случае

независимых случайных величин мы можем утверждать

(см. теорему 8 из п.З § 9), что D(x

+ ... + x

k-1

) =

= Dx

+ ... + Dx

k-1

вследствие равнораспределенности

величин x

. Таким образом, мы пришли к модели

независимых одинаково распределенных случайных

величин.

Определение 1. Выборной называется сово-

купность независимых одинаково распределенных

случайных величин, получаемых в результате слу-

чайного отбора из генеральной совокупности.

Выборочная модель наиболее разработана и нахо-

дит широкие приложения на практике. Но нельзя

забывать, что модель выборки часто бывает и неверна.

При этом могут нарушаться и требование одинако-

вости распределения случайных величин (как в при-

мере с расширением библиотеки), и требование неза-

висимости (например, при росте посещаемости библио-

теке могут увеличивать оборудование, фонды и т. д.,

что вызывает увеличение посещаемости в будущем).

В математической статистике разработаны модели,

отличающиеся от выборки небольшим числом пара-

метров, определяемым либо по части имеющихся ста-

тистических данных, либо теоретически. При этом

изучают либо отклонения от одинаковости распреде-

лений на некоторую величину, описываемую функцией

(так возникает модель тренда с ошибкой), либо откло-

нения от независимости при сохранении одинаковых

распределений (так возникает модель случайного

процесса). Мы более детально познакомимся лишь

с выборочной моделью описания статистических явле-

ний и опишем способы построения выборки, гаранти-

рующие случайный отбор объектов из генеральной

совокупности.

Сама выборка может проводиться двумя спосо-

бами.

Повторная выборка (или выборка с возвратом).

Объекты для исследования берут поочередно из гене-

ральной совокупности и возвращают после обследо-

вания. При этом не исключено, что один и тот же

объект возьмут несколько раз.

136

Бесповторная выборка (или выборка без

возврата). Объекты после обследования в генеральную

совокупность не возвращают.

Различие в этих способах выбора существенно

лишь при относительно небольших объемах генераль-

ных совокупностей.

Встречается также простой и сложный выбор. При

простом выборе объекты берут из всей генеральной

совокупности по одному. Однако в тех случаях, когда

генеральная совокупность имеет неоднородность,

предпочитают сложный (или типический) выбор. Для

этого совокупность разбивают на группы, а объекты

затем уже случайным образом выбирают из каждой

группы. Например, при изучении читательского спроса

университетской библиотеки желательно разбить

генеральную совокупность читателей на группы сту-

дентов (разных курсов или факультетов) и препода-

вателей (различной квалификации).

На практике не просто обеспечить случайность

выбора, особенно если выбор зависит от человека,

осуществляющего эту операцию. Психологами уста-

новлено, что невольно человек отдает предпочтение

определенным группам предметов или явлений даже

в тех случаях, когда стремится сделать выбор бес-

пристрастным. Поэтому для осуществления случайного

выбора на практике часто используют либо датчики,

либо таблицы случайных чисел. В таких источниках

числа появляются действительно случайным образом.

Пример. Если нужно отобрать 100 читателей и

изучить их спрос, то открывают любую страницу

таблиц случайных чисел и берут любые (хотя бы и

стоящие подряд) 100 чисел. Читатели, имеющие реги-

страционные карточки с такими номерами, и войдут

в выборку.

Наиболее универсальным и употребительным явля-

ется способ простого случайного выбора. При этом

способе на каждом шаге берется один объект сово-

купности. Он выбирается случайным образом и воз-

вращается в совокупность. Выбор следующего объекта

не зависит от результатов обследования предыдущих.

Можно отбирать для исследования каждый деся-

тый (или двадцатый, или сотый, и т.д.) объект. Та-

кой выбор называется механическим. Он не всегда

дает репрезентативную выборку.

137

Наконец, возможна и такая система отбора: если

продукция производится несколькими однотипными

и одинаково налаженными автоматами, дающими одно-

родную продукцию» то выработку одного автомата

за некоторый промежуток времени можно сделать

выборкой. При этом говорят, что произведен серий-

ный выбор.

2. Оценки параметров случайных величин.

Вероятности любых событий, относящихся к

наблюдаемой случайной величине, можно выразить

через ее функцию распределения. Следовательно, зная

приближение к функций Р(x), мы получим

приближенные значения для любых вероятностей. В

математической статистике, как правило, изучаются

такие случайные величины, у которых закон

распределения задается формулой, содержащей один

или несколько параметров. Например, в распределении

Пуассона неизвестен параметр λ, в нормальном законе

распределения Гаусса — величины σ и т и т. д.

Поэтому для приближенного определения функции

распределения достаточно иметь приближенные

значения параметров. Задача оценивания неизвестных

параметров по ряду наблюдений является одной из

основных в математической статистике. Она решается в

предположении существования распределения

вероятностей F(x) для исходной случайной величины

и применимости выборочной модели в данной

ситуации (хотя в некоторых случаях выборочная

модель не применима — не забывайте об этом).

Точечные оценки. Значение параметра θ*, вычис-

ленное на основе результатов выборки из генеральной

совокупности значений ξ, нельзя, конечно, отожде-

ствлять со значением параметра θ, характеризующего

функцию распределения. Величину θ* можно рассмат-

ривать лишь как точечную оценку значения θ.

Определение 1. Приближенные равенства

Eξ ≈ E*ξ, Dξ ≈ D*ξ называются точечными оценками

параметров Еξ и Dξ случайной величины ξ.

Так как мы решаем задачу оценивания параметров θ

с помощью параметров θ*, найденных по выборке х

... ,х

, представляющей набор одинаково распре-

деленных независимых случайных величин x

, то

Ех

= Еξ и Dx

= Dξ. Наша задача состоит в том,

чтобы найти критерии, позволяющие выбирать такие

параметры θ*, которые наилучшим образом соответ-

138

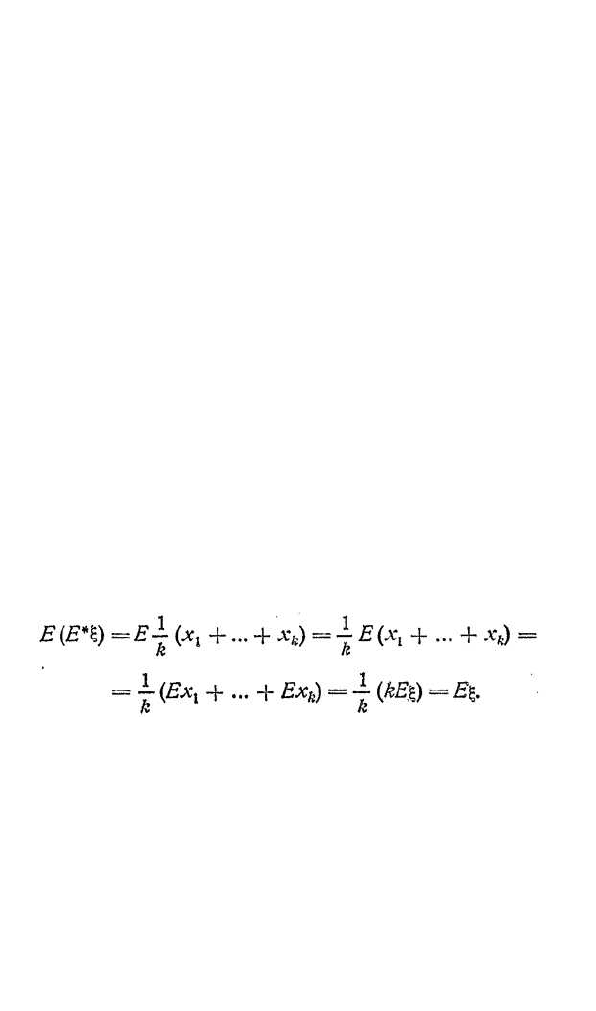
ствовали бы значению θ. Действительно, мы еще не

внаем, что является наилучшей оценкой для Eξ—ста-

тистическое математическое ожидание Е*ξ, мода Моξ

или медиана Меξ. Аналогично мы не можем сказать,

что точнее всего оценивает Dξ—статистическая дис-

персия D*ξ, вариационный размах r* или среднее

линейное отклонение d*.

В математической статистике к точечным оценкам

параметров предъявляют три требования.

Состоятельность точечной оценки для θ означает,

что для любого положительного числа ε выполняется

равенство limP(|θ — θ*|< ε) = 1, которое означает,

что при большом объеме выборки отклонения θ* от

истинного значения θ будут практически маловероят-

ны. Иными словами, параметр θ* с любой степенью

точности приближает значение 0 почти наверняка

при большом объеме выборки. Доказательство состоя-

тельности точечных оценок Еξ ≈ Е*ξ, Dξ ≈ D*ξ доста-

точно сложно, поэтому мы его не приводим.

Несмещенность точечной оценки означает, что

E(θ*) = θ. Иными словами, несмещенность оценки

гарантирует отсутствие систематической ошибки

в вычислениях. Докажем несмещенность точечной

оценки для математического ожидания, т. е. убедимся

в равенстве Е(Е*ξ) = Eξ.

Так как ЕХ

= Eξ для всех i = 1, ... , k и E*ξ =

= (x

+ ... + x

)/k, то

Несмещенность точечной оценки Dξ ≈ D*ξ, вообще

говоря, не имеет места для выборок малого объема

(k ≤ 50), Несмещенной оценкой дисперсии Dξ служит

величина — D*ξ. При больших объемах выборки

k-1

смещенность D*ξ мала, и ею обычно пренебрегают.

Эффективность точечной оценки означает, что D (θ*)

минимальная. Например, точечная оценка Eξ ≈ Е*ξ

эффективна (мы не будем этого доказывать), и мини-

мальность D(E*ξ) означает, что для любой другой

139

точечной оценки Eξ ≈ θ* (например, моды или медианы)

выполняется неравенство D (E*ξ) < Dθ*. Точечная оцен-

ка Dξ ≈ D*ξ также эффективна.

Рассмотренные выше свойства статистических ха-

рактеристик являются общими, т. е. имеют место для

любого закона распределения случайной величины.

Если же закон распределения нормален, то имеются

более точные результаты.

Интервальные оценки. Недостаток оценок θ ≈ θ*

состоит в том, что не известно, с какой точностью

они оценивают параметр. В случае большого числа

испытаний точность обычно достаточна для практи-

ческих выводов, тогда как для выборок небольшого

объема вопрос о степени точности уже существен.

Чтобы устранить этот недостаток, вводят новый тип

оценок—интервальный.

Пусть θ — неизвестный параметр распределения. По

сделанной выборке отыскивают (по определенным

правилам) числа θ

* и θ

* так, чтобы Р(θ

*< θ < θ

*) ≥

γ,

0<γ<1.

Определение 2. Числа θ

* и θ

* называются до-

верительными границами, а (θ

*, θ

*) — доверитель-

ным интервалом для параметра θ. Число γ назы-

вается надежностью сделанной оценки.

Нахождение интервальной оценки для параметра θ

начинают с того, что задают надежность γ, которую

принято выбирать равной γ

=* 0,95 при обычных иссле-

дованиях, γ

= 0,99 при исследованиях повышенной

точности и

з = 0,999 при сверхточных исследованиях.

Как правило, библиотековедческие исследования отно-

сят к категории обычных.

Мы полагаем, что события с вероятностью 0,95

и выше являются практически достоверными, следо-

вательно, попадание параметра θ в доверительный

интервал (θ

*, θ

*) также является таковым. Поэтому

середина доверительного интервала—число (θ

* +

*)/2— дает нам значение θ с точностью (θ

* — θ

*)/2 и

практически достоверно. Числа θ

* и θ

* находятся

по выборке и поэтому носят случайный характер.

Доверительный интервал (θ

*, θ

*) может покрывать

параметр θ или нет. Именно в этом смысле и

понимается случайное событие (θ

* < θ < θ

* ).

140