Елизаров А.М. Математические методы в библиотечной работе

Подождите немного. Документ загружается.

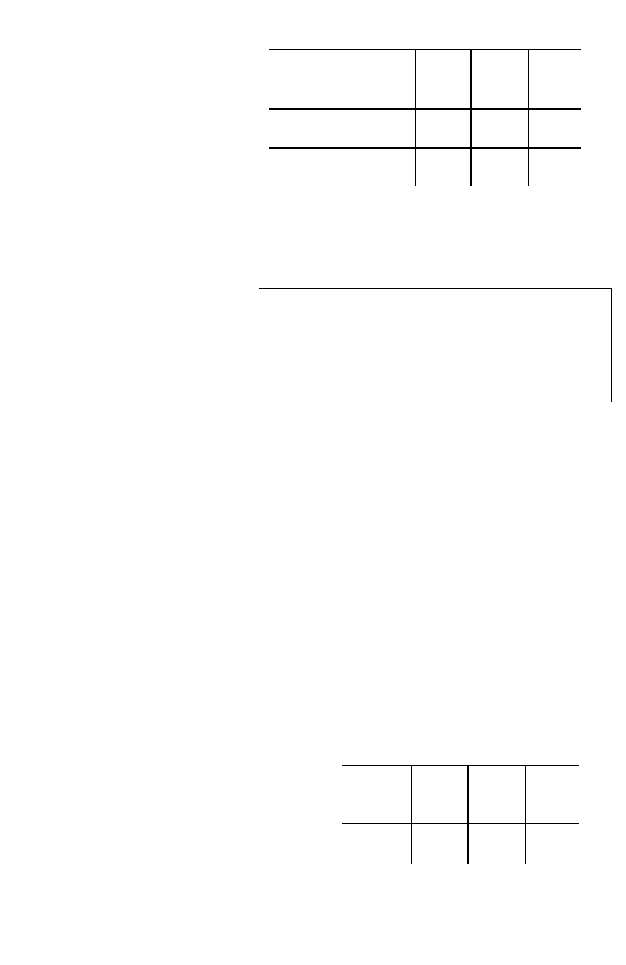
cловом, проделывать Таблица 17

все арифметические

операции по правилам

действия над числами

(табл. 17) (здесь y

—

значения другой слу-

чайной величины η на

тех же элементарных

событиях).

Часто мы будем

иметь дело с функция-

ми от случайных величин, которые также

являются случайными величинами. Так,

функция f от случай-

ной величины ξ есть

случайная величина

f (ξ), заданная табли-

цей 18.

Среди случайных

величин есть более или менее вероятные, поэтому для

полной характеристики случайной величины

необходимо иметь представление о вероятности

того или иного ее значения.

Определение 2. Законом распределения слу-

чайной величины называется соотношение, уста-

навливающее связь между вoзможными значениями

случайной величины и вероятностями появления

этих значений.

Формы закона распределения могут быть различ-

ными. Начнем со способов задания закона распреде-

ления дискретной случайной величины. Прежде всего

этот закон можно задать таблицей 19, называемой

рядом распределения.

Пример 1. Выясним закон

распределения для случайной

величины в опыте с бросанием

игральной кости. Здесь —

выпало число k — принимаем

возможные значения 1, 2, ... , 6.

При этом вероятность

появления каждой цифры одинакова, ибо события

равновозможны. Ряд распределения ξ представлен в

таблице 19а.

101

Элементарные

события

• • •

ξ + η • • • x

• • •

ξ • η • • • x

• y

•••

Таблица 18

Элементарные

события

...

_________________________________

(

)

. . .

(

)

.. .

Таблица 19

• • •

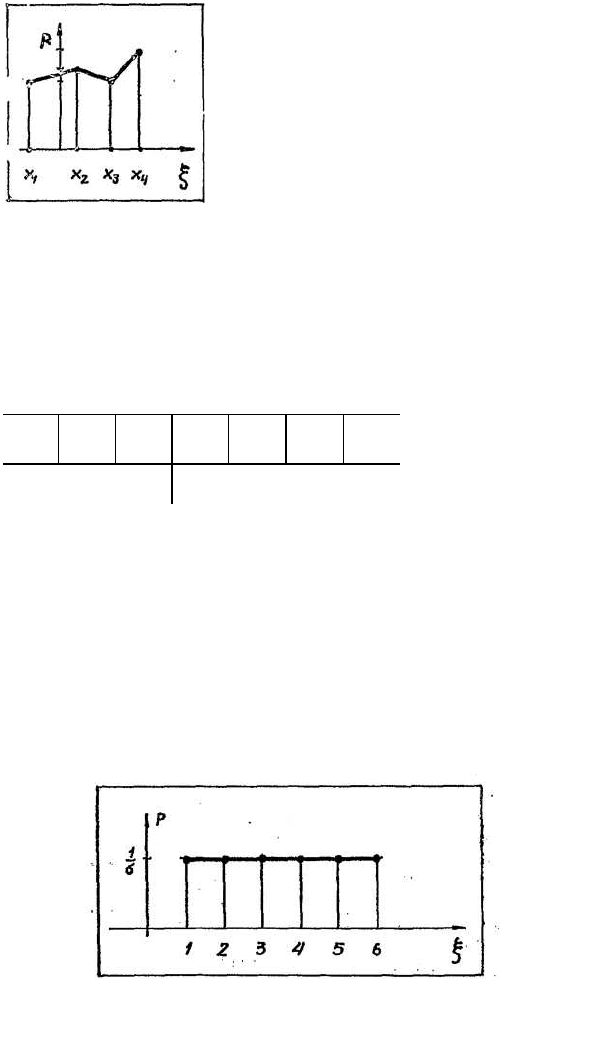
Ряд распределения можно пред-

ставить еще и в графической

форме: на горизонтальной прямой

откладывают значения ξ , а на

вертикальной — вероятности их

появления. Затем отмеченные

точки соединяют отрезками.

Получившаяся в результате фигура

(рис. 40) называется

многоугольником распределения.

Рис. 40. Многоугольник

распределения

Обратим внимание, что сумма ординат многоугольни-

ка распределения равна 1, т. к. представляет собой

сумму вероятностей всех возможных значений

случайной величины.

Таблица 19а

1 2 3 4

р 1/6 1/6 1/6 1/6 1/6 1/6

Пример 2. Построим многоугольник распределе-

ния для случайной величины из примера 1 (рис. 41).

Указанные способы задания закона распределения

хороши лишь для дискретной случайной величины,

принимающей конечное число значения. Как быть в

том случае, когда число значений бесконечно или же

требуется задать непрерывную случайную величину?

Ответ на эти вопросы дается в следующем разделе.

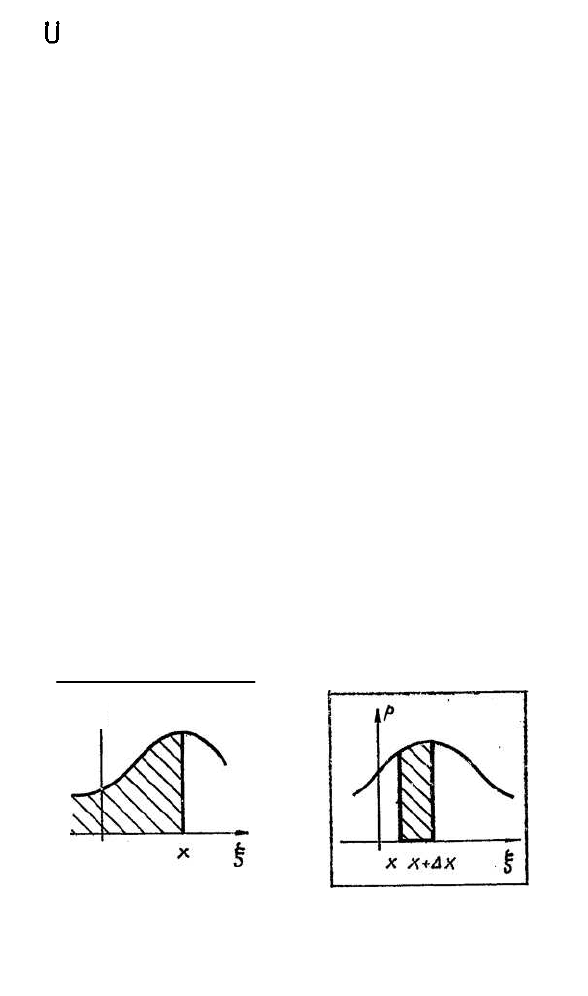
2. Функция распределения и плотность вероятности.

Прежде чем приводить строгие определения, предста-

вим, что произойдет при увеличении числа возмож-

l02

Рис. 41

Рис. 42.

Кривая распределения

Рис. 43.

Вероятность

Р(a<ξ <b)

ных значений случайной величины. Если мы начнем

строить многоугольник распредения, то при неогра-

ниченном увеличении числа значений ξ точки, изобра-

жаемые на чертеже, начнут сливаться в одну сплошную

линию и многоугольник превратится в „кривую" рас-

пределения (рис 42). Что при этом произойдет с ве-

роятностями отдельных значений ξ ? Ответить на это

нам поможет следующее усовершенствование много-

угольника распределения (рис.43). Условимся строить

его так, что расстояние между двумя соседними воз-

можными значениями равно 1 (как в примере 2 из п. 1).

Подобного можно добиться путем выбора достаточно

мелкого масштаба. Построим для каждого значения

прямоугольник высоты p

с основанием 1. Тогда

площадь каждого из элементарных прямоугольников

численно равна вероятности появления соответст-

вующего значения. Подсчитаем вероятность того, что

значения ξ попали в интервал (а, b). Численно она

будет равна сумме площадей прямоугольников, рас-

положенных над этим интервалом. Теперь начнем

увеличивать число возможных значений ξ (и умень-

шать масштаб). Тогда сумма площадей прямоуголь-

ников будет приближенно равна площади криволиней-

ной фигуры, расположенной над (а, b).

Сейчас мы готовы дать ответ на вопрос о том, что

происходит с вероятностью отдельного значения дис-

кретной случайной величины с бесконечным числом

возможных значений. Возьмем любое значение х

заключим его в некоторый интервал (а, b). Тогда

вероятность того, что а<ξ<b, есть площадь

соответствующей криволинейнрй фигуры (рис. 44).

103

Рис. 44.

Вероятность Р (a<ξ <b)

Рис. 45.

Функция распределения

Нам нужно вычислить вероятность того, что ξ = х

Для этого устремим а и b к х

. Но тогда площадь

криволинейной фигуры будет стремиться к нулю,

следовательно, и вероятность P(ξ = x

) будет стре-

миться к нулю! Аналогичные рассуждения можно

привести и для непрерывной случайной величины.

Вот что вносит бесконечность в наши допущения!

Поэтому для непрерывной случайной величины, да

и для дискретной с бесконечным числом значений,

уже невозможно задать распределения в виде ряда

или многоугольника. Тем не менее, в подобных слу-

чаях эти понятия вводятся несколько иначе, следуя

примерно по тому пути, который проделан выше, но

уже со всей строгостью.

Определение 1. Функция F(X) = P(Ξ < x), за-

дающая вероятность того, щто случайная величина

принимает значения, меньшие х, называется функ-

цией распределения.

Функция распределения позволяет полностью

описать случайную величину (как дискретную, так и

непрерывную) и поэтому является одной из форм

закона распределения. Для дискретной случайной

величины она является ступенчатой (рис. 45), причем

высота каждой ступеньки равна вероятности появления

соответствующего значения. Сама функция F (х)=

= ∑ Р(Ξ = x

), где символ x

<x означает, что сум-

мируются вероятности тех событий Ξ = х

, для кото-

рых x

<x.

Пример 1. Построим функцию распределения

для случайной величины Ξ из примера 1 п. 1. Величи-

104

Рис. 46

на Ξ может принимать значения x

= 1, х

= 2, ... ,

=6, причем во всех случаях Р(Ξ =x

) = 1/6. Тогда

функция F(x) принимает следующий вид (рис. 46):

1. На интервале —∞ < х < 1 функция F (х) = 0, т.

к. ни одно из значений Ξ не может быть меньше

1 иР( Ξ<1)=0.

2. На интервале 1≤ X<2 функция

F(x) = ∑ P(Ξ = X

) = P(Ξ = X

) = 1/6.

<х

3. На интервале 2≤х<3 F(х)=Р(Ξ=х

)+ +Р(Ξ = x

)

= 1/6 + 1/6 = 1/3. Аналогичные рассуждения проводятся

для остальных интервалов. Наконец,

4. Для 6≤х<∞ F(x) =

P(Ξ=x

)+...+P(Ξ=x

)=1. В атом можно убедиться и

иначе. В самом деле, т. к. вероятность того, что Ξ

примет значение x

≤6, равна 1, то F(x) =

= P(Ξ<x)=l для 6≤x<∞.

Отметим некоторые общие cвойства функции рас-

пределения

Свойство 1. 0≤F(x)≤1, т.к. это есть ве-

роятность случайного события.

Свойство 2. F(—∞) = 0, F(+∞) = l, что сле-

дует из определения F(x).

Свойство 3. Вероятность появления случайной

величины в интервале [а, b) равна Р(а≤ξ<b) =

= F(b) - F(a).

Доказательство. Пусть события A =

= „ξ<b", В = ,,ξ<а", C=,,a≤ξ<b". Имеем

А=ВUС и B∩C=Ø. По определению функции

распределения

105

F(b) = P(A), F(a) = P(B). Значит, F(b) = P(A) = =

P(B C) = P(B) + P(C) = F(a) + P(a≤ξ<b), откуда

следует требуемое ■.

Свойство 4. Функция F(x) не убывает, т. е. при

а<b всегда F(a)≤F(b).

Доказательство. Так как F(b) = F (a) +

+ Р(а ≤ξ<b) и вероятность Р (а ≤ ξ < b) ≥ 0, то

F(b)≥F(a) ■.

Более наглядное представление о функции распре-

деления можно получить, если отметить (ср. свой-

ство 3), что F(x) дает площадь под кривой распреде-

ления от —∞ до точки х (рис. 47). Обратите внима-

ние, что мы пока обладаем лишь неформальным по-

нятием кривой распределения, которое в дальнейшем

будет уточнено. Теперь мы можем аккуратно ввести

понятие, близкое к понятию вероятности отдельного

значения дискретной случайной величины с конечным

числом значений.

Пусть х — произвольное значение, принимаемое

случайной величиной ξ . Назовем „средней" вероят-

ностью попадания ξ в интервал (х, x + Δx) величину

вероятности события x≤ξ<x+Δx, деленную на длину

интервала. (В физике, например, подобным образом

определяют среднюю скорость движения). Теперь

осталось определить „мгновенную" вероятность

попадания ξ в точку х, т. е. заставить Δх уменьшаться, и

проследить за поведением „средней" вероятности (в

физике таким образом определяют мгновенную

скорость в заданной точке). Мы подошли к еще

одному важному понятию теории вероятностей.

Рис. 47.

F(x)=P(ξ<

<x)

Рис, 48.

P(х≤ξ<х+Δх)=

=F(x + Δx) - F(x)

106

Определение 2. Предел отношения вероятнос-

ти попадания случайной величины ξ на малый учас-

ток, примыкающий к точке х, к длине этого участ-

ка., когда последняя стремится к нулю, называется

плотностью вероятности и обозначается р(x).

График функции у = р(х) называется кривой рас-

пределения (рис. 48, 49).

3. Числовые характеристики случайной величины.

Мы познакомились с различными способами задания

случайных величин — рядом распределения, функцией

распределения, плотностью вероятности. Они пол-

ностью описывают случайную величину с вероятност

ной точки зрения. Но иногда не обязательно знать

всю информацию о случайной величине (это не всегда

возможно по ряду причин), а лишь указать ее наи

более существенные характеристики — среднее значе-

ние, вокруг которого группируются все значения, и

степень разброса значений относительно этого сред

него положения.

Перейдем к точным формулировкам. Мы опять

ограничиваемся рассмотрением дискретных случайных

величин с конечным числом значений, отмечая в не

которых случаях, как распространить установленные

факты на случай непрерывных случайных величин.

Математическое ожидание

Определение 1. Математическим ожида-

нием дискретной случайной величины ξ, заданной

таблицей 20 в опыте с п равновозможными элемен-

тарными событиями, называется число

Еξ

(х

+х

... +

)/п

= 1/n

∑x

k=1

Таблица 20

Элементарные

события

. . .

• • •

107

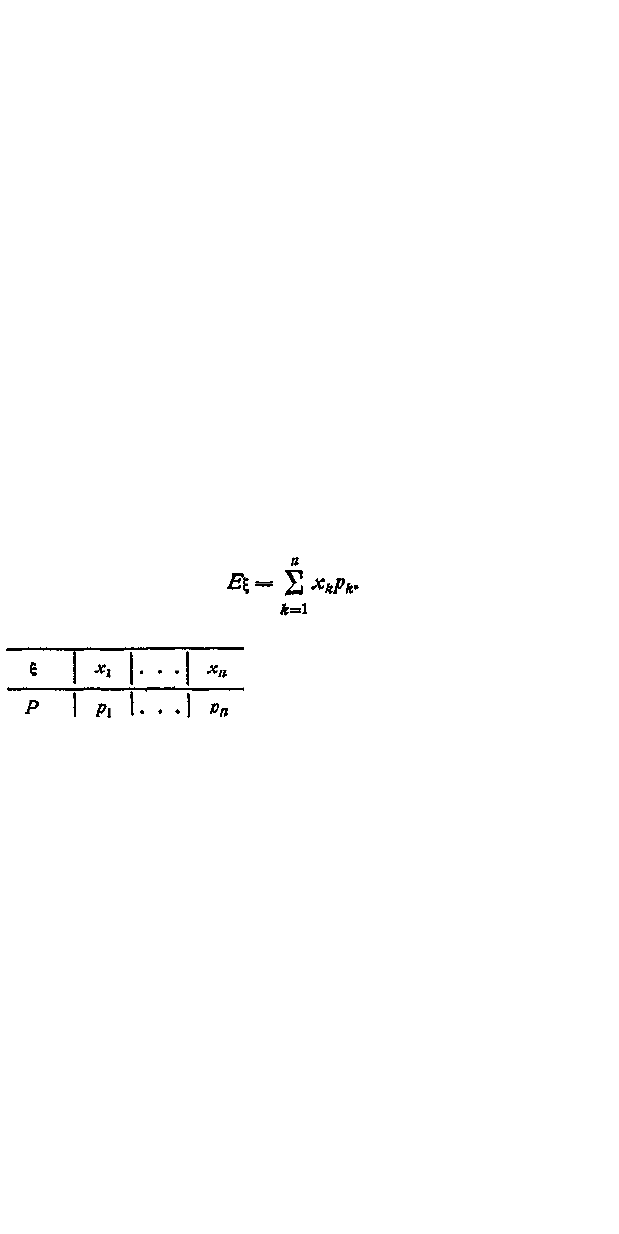
Иногда математическое ожидание называют сред-

ним арифметическим значением случайной величины.

Оно является как бы примерным, грубым приближе-

нием случайной величины. Отметим некоторые свой-

ства математического ожидания, вытекающие непо-

средственно из определения 1.

Теорема 1. Если а и b—постоянные, то

E(aξ + b)=aEξ + b.

Теорема 2. Если а и b — постоянные, то

Е(аξ)=аЕξ, Eb=b.

Эта теорема следует из предыдущей при b = 0 и

а = 0 соответственно.

Теорема 3. Для любых двух случайных величин ξ

и η E(ξ + η) = Eξ+ Eη.

Ранее мы задавали случайную величину при по-

мощи одной из форм закона распределения. Как по

закону распределения определить математическое

ожидание? Мы укажем (без доказательства) способ

его нахождения в классическом случае.

Теорема 4. Пусть дискретная случайная ве-

личина ξ задана законом распределения (рядом рас-

пределения) (табл. 21). Тогда

Т а б л и ц а 21

Приведенная теорема показывает, что в случае

опыта с равновозможными исходами математическое

ожидание случайной величины ξ можно подсчитывать как

сумму произведений значений х

случайной величины на

вероятности событий (ξ = x

). При этом события (ξ = x

вообще говоря, не равновозможны, хотя тоже образуют

множество элементарных событий. Поэтому в общем

случае, когда рассматривают опыт с неравновозможными

исходами, математическое ожидание случайной величины

определяют по формуле из теоремы 4.

Дисперсия. Кроме числовой характеристики центра

рассеивания (математического ожидания), нужны по-

108

казатели, определяющие, насколько

тесно сгруппированы возможные

значения случайной величины

около этого центра. Например,

математические ожидания

случайных величин ξ и η могут быть

одинаковы, хотя возможные

значения η могут быть более

разбросаны, чем у ξ. Хорошим

показателем разбросанности

значений является дисперсия.

Определение 2. Дисперсией

случайной велшшни ξ называется

число Dξ = Е (ξ - Еξ)

Дисперсия имеет наглядный смысл: из каждого

возможного значения случайной величины вычитается

среднее (математическое ожидание), полученное от-

клонение от среднего возводится в квадрат (чтобы

избавиться от отрицательных величин отклонения),

а затем берется „среднее" отклонение, подсчитанное

с помощью формулы для математического ожидания.

Отметим простые свойства дисперсии.

Теорема 5. Дисперсию можно вычислять по

формуле Dξ = Еξ

— (Еξ)

Доказательство. Преобразуем выражение для

дисперсии:

= E(

ξ -

ξ)

= E(

-2

+ (Е

ξ)

)

= = E

- E(2

ξЕξ

)+E(Е

)

Так как Еξ является постоянным числом, то пор тео-

реме 2

Dξ = Eξ

- 2Еξ

Еξ + (Eξ)

= Eξ

- (Eξ)

■.

Теоремаб. Если а — постоянная, mo D (aξ) = a

Dξ.

Доказательство. По определению дисперсии и

теореме 5:

D (аξ) = E(aξ)

-[E(aξ)]

= Е(a

) - (aEξ)

= a

[Eξ

- (Eξ)

] = a

Dξ ■.

109

Рис. 49. Р (a ≤ ξ < b) =

= ∫ p (x) dx

Дисперсия имеет один недостаток: ee размерность

равна квадрату размерности случайной величины, что

не очень удобно. Чтобы избежать этого, вводят новую

характеристику разброса, извлекая из дисперсии

квадратный корень.

Определение 3. Средним квадратным от-

клонением случайной величины ξ называют число

Как уже отмечалось ранее, в теории вероятностей

важную роль играет понятие независимости событий.

Распространим это понятие на случайные величины.

Определение 4. Две дискретные случайные

величины ξ и η с законами распределения называются

независимыми, если попарно независимы событий

(ξ = x

) и (η = y

), или, иными словами, для любых i

и j выполнено равенство

P((ξ = x

) ∩ (η = y

)) = P(ξ = x

) • P(η = y

Введенное понятие независимости случайных ве-

личин позволяет уточнить некоторые свойства мате-

матического ожидания и дисперсии, которые мы при-

ведем без доказательств.

Теорема 7. Если случайные величины ξ и η не-

зависимы, то

Е(ξη ) = Eξ • Eη.

Теорема 8. Для любых двух независимых слу-

чайных величин ξ и η D (ξ + η) = Dξ + Dη.

4*. Корреляция случайных величин. Довольнo

часто происходящие в действительности случайные

события взаимосвязаны, и если происходит одно из

них, то происходит и другое (хотя и не всегда). На-

пример, число читателей, обслуженных на абонементе

в течение определенного дня — случайная величина

(ξ ), количество выданных книг — также случайная ве-

личина (η). Ясно, что η зависит от ξ: чем больше

придет читателей, тем больше выдадут книг. При

этом отмеченная зависимость между случайными ве-

110

. . . х

...

•

• • •

. . .

. .

. . . Pk ...