Елизаров А.М. Математические методы в библиотечной работе

Подождите немного. Документ загружается.

решает выбор между схемами, отвечающими трем или

четырем равновозможным событиям).

3. Для получения удовлетворительного приближе-

ния к истинным результатам при решении задач, где

события в опыте не являются равновозможными. (На-

пример, мальчиков рождается больше, но мы до-

пускаем, что новорожденный имеет одинаковые шансы

оказаться мальчиком или девочкой).

Общая идея классического определения вероятно-

сти заключается в выделении из всего множества

равновозможных событий определенного подмножест-

ва благоприятных событий. При этом вероятность

указывает на шансы реализации события. Приведем

строгое

Определение. Пусть множество элементар-

ных событий состоит из п равновозлюжных исходов.

Если т из них благоприятствует событию А, то

вероятностью события А называется число Р (А) =

= m/n (Р — от английского probability — вероятность).

Отметим два простейших свойства вероятности,

вытекающих из определения:

(В

) Вероятность любого события неотрицательна,

Р(А)≥0;

(В

) Вероятность достоверного события равна 1,

P(U)=1.

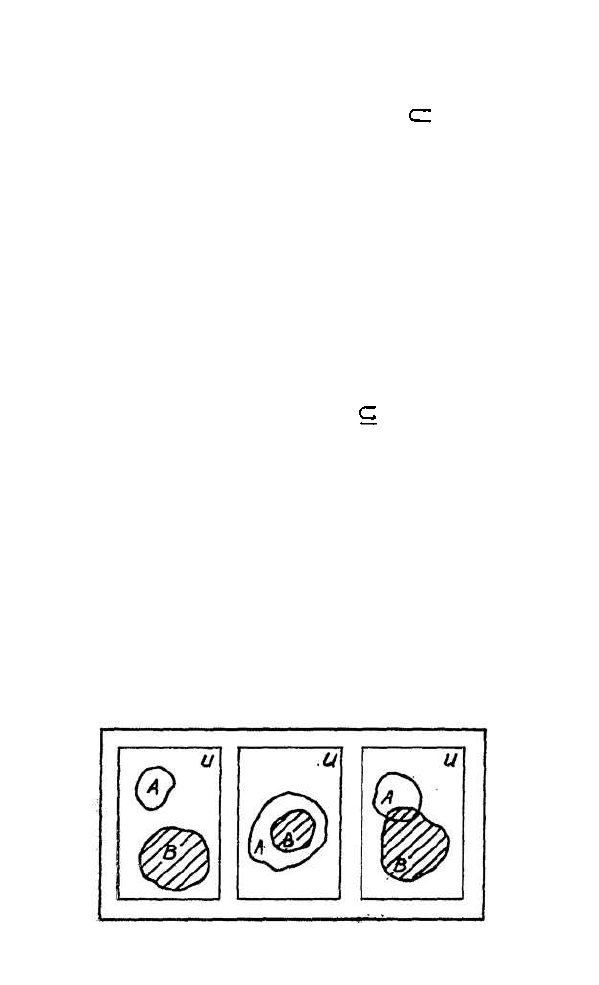
Указанная в предыдущем разделе интерпретация

событий с помощью множеств позволяет дать на-

глядное представление и о вероятности событий. Для

этого разобьем квадрат единичной площади на столько

равных квадратов (или других фигур), сколько есть

элементарных событий в опыте. Заштрихуем те из

квадратов, которые благоприятствуют событию А.

Тогда Р(А) будет численно рав-

няться площади заштрихованной

фигуры (рис. 36).

Пример 1. Вычислим ве-

роятность события Q

в опыте с

мини-библиотекой. Здесь число

п = 10. Событию Q

благо-

приятствуют элементарные со-

бытия Q

, Q

, т. е.

m = 5. Поэтому P(Q

) = 1/2.

Эту задачу можно решить и по-

другому. Выше мы отмечали,

6 Т-743

Рис.

Вероятность Р(А)

что {Q

, Q

} также] представляет множество элемен-

тарных событий. В этом случае п = 2, а m=1, сле-

довательно, P(Q

) = 1/2, что вполне согласуется с

предыдущим решением.

Пример 2. Определим вероятность выпадения

двух гербов в опыте с подбрасыванием двух монет.

Имеем: n = 4, m = 1, значит, Р(ГГ) = 1/4.

Опишем теперь схему введения понятия вероят-

ности в опыте с конечным числом равновозможнмх

событий. Если множество элементарных событий сос-

тоит из п равновозможных исходов, то каждое эле-

ментарное событие получает вероятность 1/п. Веро-

ятность события А определяется сложением вероят-

ностей всех элементарных событий, входящих в со-

бытие А.

Сейчас мы обратимся к задаче определения по

вероятностям одних случайных событий вероятности

других случайных событий. Простейшие результаты,

относящиеся к этой задаче, получили название тео-

ремы сложения.

(ВЗ) Если события А и В несовместны, то

Р(А В)=Р(А) + Р(В).

Доказательство. Пусть рассматриваемый опыт

состоит из п равновозможных элементарных событий

и т из них благоприятствуют событию A, a k бла

гоприятствуют событию В. Поэтому P(A)=m/n,

а Р(В)=k/п. Поскольку события А и В несовместны

(А∩В = Ø), то нет элементарных событий, благопри

ятствующих одновременно и А, и В. Следовательно,

событию А В благоприятствуют т + k исходов

(т благоприятствуют событию А, k — событию В).

Тогда

Р (А В)= (m + k)/n= m/n + k/n = P (A) + Р(В)

Рассмотрим произвольный случай.

Теорема 1. Пусть А и В — произвольные собы-

тия. Тогда

Р(А В)=Р(А)+Р(В)-Р(А∩В).

Доказательство. Р(А В) есть сумма вероят-

ностей элементарных событий, входящих как в А,

так и в В. С другой стороны, Р(А)+Р(В) равна

сумме вероятностей элементарных событий, состав-

ляющих А и В. Очевидно, что в этой сумме дважды

учтены вероятности событий, благоприятствующих

одновременно как А, так и В, т.е. входящих в A ∩ B.

Вычитая Р(А∩В) из суммы Р(А) + Р(В), получаем

сумму вероятностей, составляющих Р(А В), что в

требовалось доказать

Пример 3. Читатель берет на выставке новых

поступлений одну заинтересовавшую его книгу по

литературе или искусству. Вычислим вероятность.

того, что читатель выбрал книгу по литературе или

искусству, если вероятность выбора книги по лите-

ратуре равна 0,5, а книги по искусству — 0,3. Опыт

состоит в том, что читатель посетил библиотеку и

выбрал одну из новинок. Событие А = „читатель вы-

брал книгу по литературе", событие В = „читатель-

выбрал книгу по искусству". Эти события несовместны,

т. к. выбирается только одна книга. Поскольку нас

интересует событие А

= „читатель выбрал книгу

по литературе или искусству", то

Р(А В) = Р(А)+Р(В) = 0,3 + 0,5 = 0,8.

Может возникнуть вопрос: откуда известны вероят-

ности выбора книг? Ответ: из изучения читательского

спроса в течение ряда лет.

Отметим еще одно свойство, связывающее собы

тия

Ā.

Теорема 2. Вероятность события Ā может

быть вычислена по формуле Р(Ā) = 1-Р(А).

Доказательство. Так как А Ā = U неверо-

ятность P(U) = 1 (см. свойство В2), то Р(А Ā) = 1.

Но события А и Ā несовместны, следовательно (по

свойству В3), 1 = Р(А Ā)=Р(А) + Р(Ā), откуда и

следует утверждение теоремы

Пример 4. Вычислим вероятность события Q

в опыте с мини-библиотекой. Так как Q

= Q

, а ве-

роятность P(Q

) = l/2 (см. пример 1), то P(Q

)= =

1 — P(Q

) = 1 - 1/2 = 1/2. Здесь мы воспользовались, тем,

что Q

∩Q

= Ø, И применили теорему 2.

3. Условная вероятность. В предыдущих разделах

мы широко применяли связь между понятиями алгебры

множеств и алгебры событий. Но теория вероятно-

стей изучает ряд понятий, специфичных для науки

о случайном и не имеющих прямых аналогий в теории

множеств. Если бы это было не так, то теория ве-

роятностей представляла бы собой скучный перевод

фактов из теории множеств на свой, вероятностный

язык. Одним из таких сугубо вероятностных понятий

является понятие независимости событий, к обсужде-

нию которого мы переходим.

Пример 1. Вернемся к опыту, связанному с бро-

санием двух монет —медной и серебряной. Множество

элементарных событий в этом опыте состоит из

{ГГ; ГЦ; ЦГ; ЦЦ}, где первая буква указывает на

выпавшую сторону медной монеты, а вторая — сереб-

ряной. Вычислим вероятность события ГЦ = „на

медной монете выпал герб и на серебряной монете

выпала цифра", представляющего собой событие

∩Ц

. Очевидно, что Р(Г

∩Ц

) = 1/4. С другой

стороны, вероятность того, что в опыте с подбрасы-

ванием медной монеты выпадет герб, равна Р(Г

) =1/2.

Точно так же P(Ц

) = 1/2. Мы считаем, что выпаде-

ние герба на одной монете никак не влияет на выпа-

дение герба на другой монете. В этом случае вычис-

ления показывают, что Р(Г

∩ Ц

)= 1/4 = 1/2 • 1/2 =

= Р (Г

) • Р (Ц

). Полученная формула подсказывает

способ строгого определения независимых событий.

Определение 1. События А и В называются

независимыми, если выполняется условие

Р(А∩В)=Р(А)•Р(В).

Отметим полезное свойство независимых событий.

Теорема 1. Если А и В — независимые события с

положительными вероятностями, то они совместны.

Доказательство. Мы должны убедиться, что

А∩В≠Ø. Допустим, что это не так и А∩В=Ø.

Тогда 0 = Р(Ø) = Р(А ∩В) =Р(А)•Р(В). Следовательно,

либо Р(А) = 0, либо Р(В) = 0. Но это противоречит

условию теоремы. Значит, наше предположение

неверно

Часто приходится определять вероятности одних

событий после того, как уже произошли другие со-

бытия. Меняется ли при этом вероятность? Очевидно,

да. Например, вероятность того, что выбранная из

данного количества книга окажется технической,

изменится, если предварительно убрать с полки все

книги по зарубежной литературе. Как описать эту

взаимосвязь?

Начнем с простейших случаев. Так, если А и В

несовместны, то А произойти после В уже не может-

Здесь А играет роль невозможного события — его

вероятность равна нулю. Если же В А, то А всегда

происходит после того, как произошло В — в этой

ситуации событие А играет роль достоверного собы-

тия с вероятностью единица. Для того, чтобы оха-

рактеризовать промежуточный случай, вводится по-

нятие условной вероятности.

Определение 2. Условной вероятностью со-

бытия А при условии, что произошло событие В,

Р(В)≠0, называется число

Р(А|В)=Р(А∩В)/Р(В).

Как согласуется это определение с рассмотренны-

ми выше случаями? Если А и В несовместны, то

А∩В=Ø, Р(А∩В)=0, значит, Р(А|В) = 0. Если В

благоприятствует А, т, е. В А, то А∩В=В и

Р(А∩В)=Р(В). Значит, Р(А | В) = Р(В)/Р(В) = 1. Со-

гласование полное.

Нетрудно заметить, что условная вероятность

численно выражает часть площади фигуры А, которую

она составляет в площади фигуры В (рис. 37).

Пример 2. При информационном поиске необ-

ходимо задавать критерий соответствия ПОД и ПОЗ.

Обычно ИПС обладает своим порогом релевантности,

и другой порог устанавливает пользователь системы.

Для принятия конкретного поискового решения на

практике пользуются следующим правилом: документ

нужно выдавать, если вероятность его релевантности, с

точки зрения пользователя, выше, нежели вероят-

Рис. 37. Условная вероятность Р(А|В)

ность его релевантности в ИПС. Тем самым обеспе-

чивается большая полнота поиска. В этом примере

вероятность релевантности документа с точки зрения

пользователя представляет собой условную вероят-

ность события, которое происходит лишь тогда, когда

отыскан релевантный (с точки зрения системы) до-

кумент.

Укажем некоторые свойства условной вероятности.

Теорема 2. Если события А и В независимы и

имеют положительные вероятности, то

Р(A|В)=Р(А), Р(В|А)=Р(B).

Доказательство. Так как А и В независимы,

А∩В = В∩А, то Р(А∩В) = Р(В∩А) = Р(А)•Р(В).Раз

Р(А)>0, Р(В)>0, то разделив обе части равенства

на Р(В), получим

Р(А|В) = Р(А∩В)/Р(В)=Р(А)•Р(В)/Р(В)=Р(А), а

разделив на Р(А), получим Р(B | А) = Р(В ∩ А)/Р(А) =

= Р(А)• Р(В)/Р(А) = Р(В)

Особенно просто вычисляется условная вероят-

ность в случае множества с равновозможными исхо-

дами.

Теорема 3. Если событию В благоприятствуют

m(>0) равновозможных элементарных событий и к

из них благоприятствуют событию А, то

P(A|B) = k/m.

Доказательство. Пусть в опыте п элементар-

ных событий. По условию теоремы P(B) = m/n, а

P(A∩B) = k/n. Тогда

Р (А | В) =Р(А ∩ B)/P (B)=(k/n)/(m/n) = k/m

Пример 3. ИПС выдает пользователю документ

из 10 дескрипторов (среди которых есть несоответ-

ствующие запросу), если при просмотре двух из них,

выбранных наугад, будет установлена релевантность.

Какова вероятность того, что ИПС отыщет документ,

содержащий 4 нерелевантных дескриптора?

Пусть событие А

= „первый дескриптор документа

есть в ПОЗ", а событие A

= „второй дескриптор

документа есть в ПОЗ". Нас интересует вероятность

события A

∩A

. По формуле условной вероятности

Р(А

∩ A

) = Р(А

)•Р(А

| А

). Имеем Р(А

) = 3/5 (среди 10

дескрипторов выданного документа 6 релевантных).

Далее, событие A

состоит в том, что из 9 деск-

рипторов, среди которых 5 релевантных (один из ре-

левантных отыскали в событии A

), нужно найти ре-

левантный дескриптор. В этом случае Р(А

|А

) = 5/9.

Окончательно, Р(А

∩А

) = 3/5•5/9= 1/3. Значит, при-

мерно в одном случае из трех при подобной страте-

гии поиска ИПС выдаст документ с четырьмя нере-

левантными дескрипторами.

4*. Некоторые сведения из комбинаторики. Если

число элементарных событий очень велико, то метод

их выписывания становится непригодным. Однако

здесь можно обойтись и без перечисления всех ва-

риантов, если воспользоваться некоторыми результа-

тами комбинаторики — математической науки, изучаю-

щей комбинации и перестановки элементов конечных

множеств. Мы рассмотрим две основные задачи ком-

бинаторики и укажем формулы для расчетов.

Число перестановок. Пусть имеется мно-

жество из п элементов. Перестановкой элементов

множества называется их размещение в определенном

линейном порядке. Число таких перестановок обозна-

чается Р

. Мы хотим найти формулу для Р

. Начнем с

простого случая.

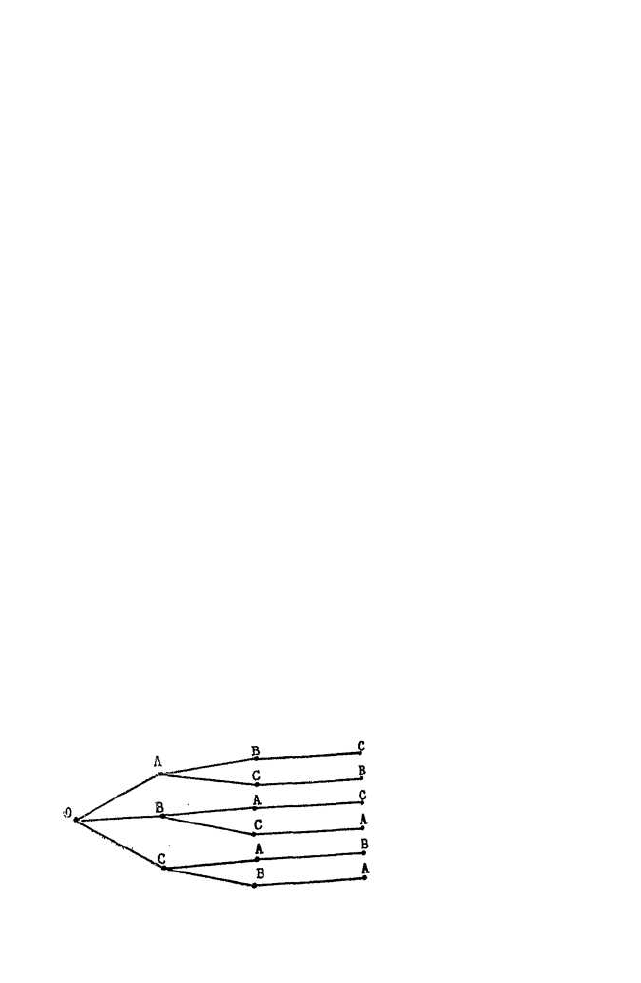
Пример 1. Выясним, сколькими способами можно

расставить на полке три книги А, B, С.

Выпишем дерево всех возможных размещений

(рис. 38).

Рис. 38

аэмещени

Книга

м м

Книга на

ес

Книга на

1-м месте

ачало

ABC

АС8

ВАС

ВСА

CAB

СВА

Кратко наш способ рассуждений можно представить

так. На первое место можно поставить любую из

книг, т. е. можем заполнить его тремя способами.

Для каждого из трех вариантов заполнения первого

места есть две возможности заполнения второго места.

Теперь первые два места мы можем заполнить 3•2

способами. Для каждого из этих 6 вариантов есть

только одна возможность заполнения третьего места.

Таким образом, всего имеется 3•2•1 способов рас-

становки трех книг. При решении примера 1 мы

использовали удобный универсальный метод, в основе

которого лежит следующее утверждение.

Принцип умножения. Пусть необходимо выполнить

одно за другим к действий. Если первое действие

можно выполнить п

способами, после чего второе

действие можно выполнить n

способами, и т. д. до k-

го действия, которое можно выполнить n

способами,

то все k действий можно выполнить п

• п

... n

способами.

Напомним, что произведение всех натуральных

чисел от 1 до п называется факториалом числа п и

обозначается п!:

п! = n(n — 1)...2•1, 0! = 1 (по определению).

Непосредственным следствием принципа умноже-

ния является следующее утверждение.

Теорема 1. Число перестановок из n элементов

=n!

Число сочетаний. Нас интересует вопрос, сколько

различных подмножеств из т элементов можно вы-

брать из множества, включающего п элементов (п ≥ т).

Перестановкой из п элементов по r называется

произвольное размещение r элементов, которые при-

надлежат множеству из n элементов (r ≤ n). Общее

число таких перестановок обозначается Р

Выше мы рассматривали перестановки вида Р

нашли для них формулу Р

= Р

= п!. Сформулируем

более общий результат. Известна

Теорема 2. Число перестановок из элементов

по r равно

=п!/(п-r)!

Пример 2. Сколькими способами из семи книг

можно отобрать три и расставить их на книжной

полке?

Для решения необходимо найти P

. Имеем

= 7!/4! =7•6•5 = 210.

Во многих комбинаторных задачах не играет роли

порядок следования предметов. В связи с этим вво-

дится следующее понятие.

Сочетанием из п элементов по r называется произ-

вольное неупорядоченное r-элементное подмножество

множества из n элементов. Общее число таких соче-

таний обозначают С

или (

). Имеет место

Теорема 3. Число сочетаний из п элементов

по r равно

=n!/[r!(n-r)!].

Пример 3. Сколькими способами читатель мо-

жет отобрать три книги из четырех, если порядок

книг его не интересует?

Решение: C

=4!/[3!(4 — 3)!] = 4.

Приведем пример на вычисление вероятности со-

бытия в опыте с большим числом элементарных со-

бытий.

Пример 4. В читальном зале находится 30 жур-

налов — 20 советских и 10 зарубежных. Случайным

образом отбираются 5 журналов для анкетирования.

Какова вероятность того, что в число отобранных

войдут; а) только советские журналы; б) в точности

два зарубежных издания?

а) Количество всех равновозможных наборов из

30 элементов по 5 равно С

= 142506. Набор, состоя-

щий из советских журналов, может быть выбран

= 15504 способами. Таким образом, 15504 элемен-

тарных события из 142506 благоприятствуют событию

A=,,набор состоит из советских журналов". Следо

вательно, Р(А) = С

= 15504/142506 ≈ 0,109.

б) Отбор 2 зарубежных и 3 советских журналов

можно осуществить C

•C

способами. Поэтому

вероятность события B=„в наборе 2 зарубежных и

3 советских журнала" равна

P(B) = C

•C

= 51300/142506 ≈ 0,36.

§ 8. Вероятность

Предыдущий параграф был посвящен построению

теории вероятностей в классическом случае для рав-

новозможных элементарных событий. Однако на прак-

тике это далеко не всегда выполнимо, и поэтому

приведенная схема изучения вероятности не срабаты-

вает. Необходимо избирать другой путь построения

модели, достаточно правильно отражающей понятие

вероятности случайного события. Мы укажем общий

подход к созданию теории вероятностей, охватываю-

щий все наиболее распространенные частные случаи

и получивший надежное экспериментальное подтверж-

дение.

I. Неравновозможные события и вероятность.

Начнем с рассмотрения опыта, требующего отказа от

классической схемы введения вероятности.

Пример 1. Возьмем волчок, представляющий из ceбя

диск с прикрепленным перпендикулярно к его центру

заостренным стержнем (рис. 39). Произведем опыт,

заключающийся в том, что волчок подбрасывается

вверх, затем падает на твердую поверхность, где

вращается до полной остановки. Остановившись он

может оказаться в двух положениях: А — острием

вверх, В—острием вниз. Проведенный опыт имеет

ровно два неравновозможных элементарных события

и нет явного способа определить вероятность каж-

дого из них. Каждый раз при бросании волчка ра-

зумно предположить, что событие А имеет опреде-

ленную вероятность Р(А) = р. Но даже тщательно

осмотрев волчок, невозможно сказать, чему равно

значение р. У нас нет никаких оснований полагать

р = 1/2, как в опыте с монетой, ведь волчок несим-

метричен и элементарные события А

и В, конечно, неравно-возможны.

Ясно, что классическое

определение вероятности здесь

неприменимо.

Как поступать в подобных

случаях? Что можно выбрать

за вероятность событий А? По

пробуем несколько раз повто

рить наш опыт и выяснить, ка-

Рис. 39 кое событие (А или В) проис-