Елизаров А.М. Математические методы в библиотечной работе

Подождите немного. Документ загружается.

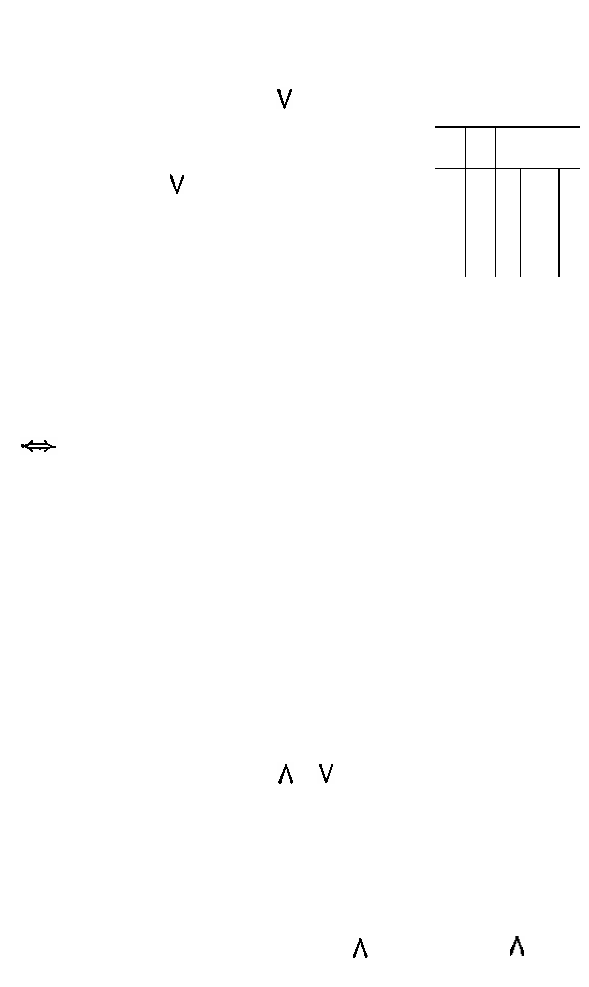
истинно, а при других — ложно. Выяснение значений

истинности сложных высказываний достигается путем

построения таблиц истинности.

Пример. Построим таблицу истин-

ности для высказывания

В. Для Таблица 10

этого перечислим комбинации всех

возможных значений истинности для

высказываний A и В. Затем в сложном

высказывании

В выполним последо-

вательно все операции — сначала отри-

цание Ā, а потом дизъюнкцию Ā и В.

Результат каждой выполненной опера-

ции записывается в таблице истинности

под знаком соответствующей операции.

Мы видим, что построенная таблица имеет точна

такой же вид, что таблица истинности для высказы-

вания А→В. В математической логике такую ситуацию

описывают следующим образом.

Определение 6. Два высказывания X, У на-

зываются равносильными (обозначается

X У), если при любых значениях истинности

логических переменных, входящих в X и У, их

таблицы истинности совпадают.

Таким образом, с точки зрения логики, два равно-

сильных высказывания утверждают одно и то же,

они взаимозаменяемы.

3. Дизъюнктивные нормальные формы. В преды-

дущем разделе мы познакомились со способом опре-

деления значений истинности произвольного сложного

высказывания через таблицы истинности. Часто

представляет интерес и обратная задача: по известной

таблице истинности найти одно или несколько

высказываний с этой таблицей (ясно, что все они

равносильны). В исчислении высказываний доказано,

что обратная задача всегда имеет решение, содержа-

щее лишь операции ,

и —. Мы укажем

способ (в математике говорят „алгоритм") построения

высказывания по заданной таблице истинности,

ограничившись случаем двух логических

переменных.

Введем несколько вспомогательных понятий. Эле-

ментарной конъюнкцией называется сложное выска-

зывание, в котором логические переменные или их

отрицания соединены операцией

Например, А

В,

4* 51

А В

Ā\/

и и

и л

л л

л и и и

л и и

ĀΛB — элементарные конъюнкции» тогда как А

Λ(

А)

такой не является.

Определение 1. Дизъюнктивной нормальной

формой (ДНФ) высказывания называется дизъюнк-

ция элементарных конъюнкций, равносильная исход-

ному высказыванию.

Понятие ДНФ играет важную роль в математи-

ческой логике, т. к. любое высказывание можно

представить при помощи ДНФ и в дальнейшем опе-

рировать с ДНФ, имеющей более простую структуру-

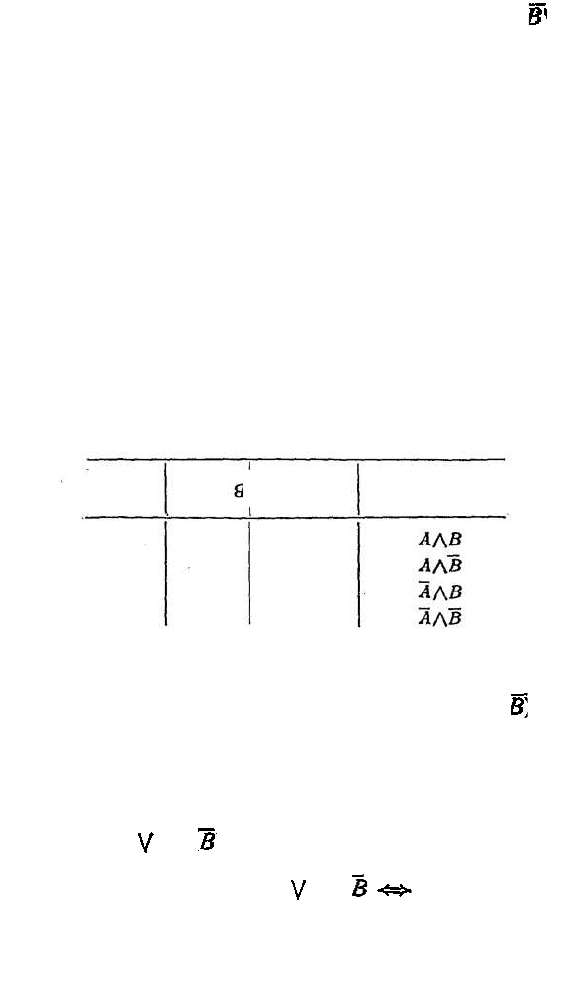
Алгоритм построения ДНФ. Пусть задана

таблица истинности и необходимо по ней построить

высказывание. Составим элементарные конъюнкции

ио следующему правилу: берем конъюнкции всех

логических переменных или их отрицаний соответ-

ственно тому, стоит ли под этой переменной в стро-

же, где написана конъюнкция, значение ,,и" или ,,л"

(см. табл. 11). Затем строим дизъюнкцию всех эле-

Таблица 11

ментарных конъюнкций, которые стоят в строках,

соответствующих значению „и" за данной таблицы

истинности. В данном примере это (А/\В)\/(

ĀΛ

Полученное в результате высказывание записано

в дизъюнктивной нормальной форме и имеет требуе-

мую таблицу истинности. На доказательстве изложен-

ных фактов мы останавливаться не будем.

Полученное в результате построения высказыва-

ние (АΛВ) (ĀΛ ) имеет таблицу истинности

такую же, как и А←→В. Поэтому мы можем

утверждать, что (АΛВ) (

ĀΛ

) А←→В, т. е.

найденную ДНФ можно упростить.

4*. Алгебра высказываний. При исследовании зна-

чений истинности высказываний нам приходилось в

Таблица

истинности

Элементарные

конъюнкции

.л

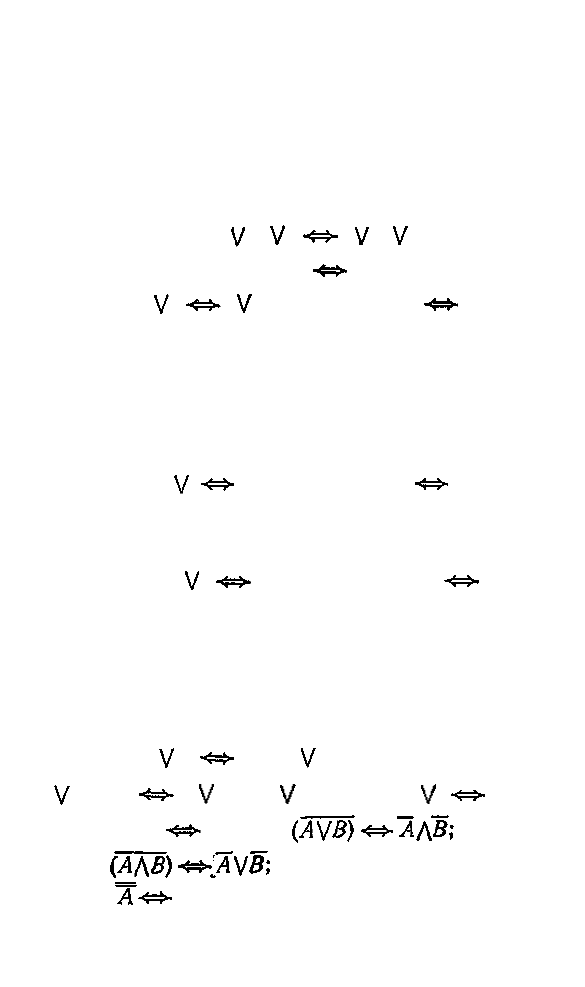
каждом случае строить таблицу истинности. Хотя

такой метод может быть и утомительным, он всегда

приводит к цели. Другой путь решения поставленной

задачи связан с введением понятия равносильных

высказываний, которое позволяет упрощать сложные

высказывания. Подобно тому, как алгебра чисел ос-

нована на нескольких основных равенствах, алгебра

высказываний (или, как иногда говорят, алгебра ло-

гики) основана на нескольких основных равносиль-

ностях. Приведем несколько примеров:

(АЛ1)(А В) С А (В С);

(АЛ1') (AΛB)ΛC AΛ(BΛC);

(АЛ2)А В В А; (АЛ2') АΛВ ВΛА.

Сравните эти равносильности с формулами алгебры

множеств — как много сходства. Мы продолжим эту

аналогию. В алгебре множеств особую роль играли

универсальное множество U и пустое множество Ø.

Подобную роль в алгебре логики выполняют логи-

ческие постоянные "и" и „л".

(АЛ3)А

и;

(АЛ3')АΛл л.

Следующие две равносильности также похожи на

равенства алгебры множеств:

(АЛ4) А

и; (АЛ4')АΛĀ л.

Это закон исключенного третьего (либо имеет место

„А", либо „не A"— третьего не дано, поэтому выска-

зывание „А или не А" всегда истинно) и закон про-

тиворечия (высказывания „А" и „не А" не могут

выполняться одновременно). Приведем еще ряд по-

лезных равносильностей:

(АЛ5)АΛ(В С) (АΛВ) (АΛС); (АЛ5')

А (ВΛС) (А В)Λ(А С); (АЛ6) А А А;

(AЛ6') АΛА А; (АЛ7)

(АЛ7')

(АЛ8) А.

Равносильности (АЛ7) и (АЛ7'), как и в алгебре

множеств, называются законами де Моргана, а со-

отношение (АЛ8) получило название закона двойного

отрицания.

Отмеченное сходство между алгеброй множеств

и алгеброй логики не случайно — далее мы укажем,

что в некотором смысле эти две алгебры являются

различными формулировками одной и той же теории.

Как установить справедливость этих равносиль-

костей? Укажем полезный способ проверки, который

можно применить в данной ситуации.

Теорема. Логические выражения X и У равно-

сильны в том и только в том случае, когда экви-

валенция Х←→У истинна при всех значениях логи-

ческих переменных.

Доказательство. Пусть выражения равносиль-

ны: X У. Это означает, что для любой комбинации

значений логических переменных X и У одновременно

или истинны, или ложны. Но тогда эквиваленция

Х←→У истинна.

Пусть теперь X←→У истинна при любых наборах

значений переменных. Это возможно лишь тогда,

когда X и У либо одновременно истинны, либо одно-

временно ложны, что указывает на равносильность

X У .

Отметим разницу между эквиваленцией и равно-

сильностью: эквиваленция — это логическая операция,

позволяющая по двум высказываниям строить новое,

а равносильность — это отношение между высказы-

ваниями» состоящее в том» что значения истинности,

этих высказываний всегда одни и те же.

Логические выражения» истинные при любых зна-

чениях истинности входящих в них переменных, на-

зывают тождественно истинными или тавтологиями

(от греческого „тауто"— то же самое, ,,логос" —

слово).

Пример 1. Докажем один из законов де Моргана

(АЛ7): Для этого построим таблицу

истинности для , и убедимся, что она

является тавтологией (табл. 12).

Покажем, как на основе знания основных равно-

сильностей можно упрощать сложные высказывания.

Пример 2. Упростим сложное высказывание

Та б л и ца 12

Равносильность 1— это (АЛ7'), 2 — (АЛ8), 3 (АЛ1),

4-(АЛ4), 5-(АЛЗ).

§ 5. Исчисление предикатов

Теория, которую дает нам исчисление высказыва-

ний, недостаточна для математики и приложений.

Так, простейший силлогизм „Все люди смертны.

Сократ — человек. Следовательно, Сократ смертен"

уже не может быть доказан в рамках исчисления

высказываний. Объяснимо это тем, что в исчислении

высказываний интересуются лишь истинностью со-

ставных частей высказывания, тогда как для проверки

сделанного выше логического вывода необходим

анализ структуры самого высказывания.

Сейчас мы обращаемся к изучению высказываний

на втором, более глубоком уровне, который осуществ-

ляется в разделе математической логики, называемом

исчислением предикатов.

1. Высказывательные формы. Начнем с простых

примеров. Высказывания „Все книги печатные",

„Некоторые книги рукописные" — сходны, но в то

же время отличны по форме строения друг от друга.

В самом деле, первое утверждает, что некоторое

свойство присуще всем книгам, тогда как во втором

идет речь о свойстве, которым обладают лишь не-

которые из книг.

Анализ показывает, что эти высказывания состоят

аз трех частей. Одной из них является подлежащее

„книги", характеризующее множество объектов, от-

носительно которого делается данное высказывание.

Второй частью являются сказуемые „печатные" или

„рукописные". Сказуемое называют предикатом (от

латинского praedicatum). Наконец, в высказывания

входят слова „все" или „некоторые", указывающие

на количество элементов с данным свойством. Эти

слова называют кванторами (от латинского quantum —

количество).

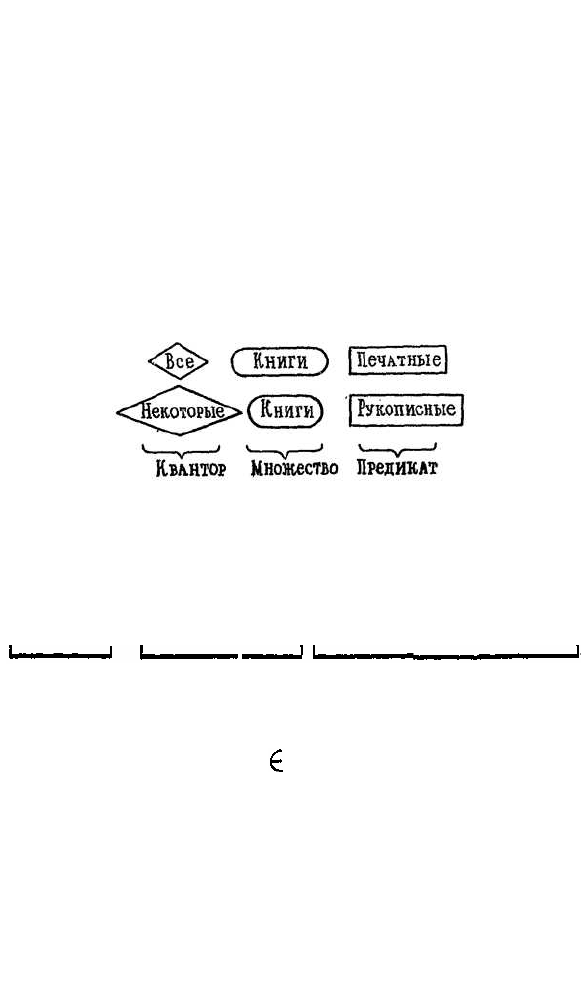
Подведем итоги. Высказывания, касающиеся

свойств некоторого множеству состоят из описания

этого множества, указания свойств (предикатов) и

квантора, показывающего, обладают ли этим свой-

ством все элементы множества или лишь некоторые

из них (рис. 28).

Рис. 28.

Таким высказываниям можно придать следующую фор-

му:

Для всех х из множества X выполняется свойство Р(x),

Некоторые х из множества X обладают свойством Р(x),

Квантор множество предикат

Часть высказывания ,,х из множества X, обладающая

свойством Р(х)" называется высказывательной фор-

мой и обозначается ,,х X Р(х)", или, сокращенно,

Р(х). Сразу же подчеркнем, что высказывательная

форма не является высказыванием (пока не выбран.

элемент х из множества Х, нельзя проверить, выпол-

нено для х свойство Р или нет). Иногда Р(х) назы-

вают высказыванием со свободной переменной.

Чтобы получить из высказывательной формы выска-

зывание, необходимо подставить вместо х опреде-

ленный элемент а из множества X; в результате обра-

зуется высказывание Р(а).

Пример 1. A (х) = „х — рукописная, х принадле-

жит множеству книг"— не высказывание, а высказы-

тельная форма. Она может принимать на множестве

книг как истинное, так и ложное значения. А вот

„Книги сошного письма — рукописные" — высказыва-

ние, т. к. мы всегда можем проверить, истинно оно

или ложно.

Пусть высказывательные формы А (х), В (х), ... за-

даны на одном и том же множестве X (мы опускаем

х X в записи форм). Тогда с помощью логических

операций из них можно строить новые выражения вида

А(х)/\В(х), А(х)

→

А(х)

←→В(х) и т. д., которые

также будут выеказывательньши формами.

Действительно, если в каждом из таких выражений

заменить переменную х каким-то значением а X, то

получится сложное высказывание, составленное из

высказываний А (а), В (а),... Поэтому основные пра-

вила алгебры высказываний распространяются и на

алгебру высказывательных форм.

Пример 2. Пусть А(х) =,,х — рукописная", B(x) =

,,x — древнерусская" и обе эти формы заданы на

множестве книг X. Тогда сложные высказывательные

формы, указанные выше, означают:

А (х) Λ В (х)-— ,,х — древнерусская рукописная книга",

А(х)

→

—„если х рукописная, то х недревнерус

ская книга",

А(х)←→В{х)- ,,х рукописная книга тогда и только

тогда, когда х — древнерусская".

2. Кванторы. В исчислении предикатов по сравне-

нию с алгеброй высказываний появляются новые,

дополнительные логические операции квантификации,

которые делают его значительно богаче по содержа-

нию. Эти операции также позволяют превращать

высказывательные формы в высказывания. Для этого

реред высказывательными формами записывают кван-

торы. Они имеют специальные обозначения и назва-

ния: вместо слов „для всех х" пишут х и называют

квантором всеобщности, а вместо слов „существует

х» пишут х и называют квантором существования.

Символ

произошел от английского слова Аll —

все, а символ

— от английского Exist —

существовать. Кванторы х и х называют

двойственными друг другу.

Определение 1. Универсальным высказыва-

нием называется

X Р(х) (читается „для

всех х, принадлежащих X, выполнено Р(х)"), которое

считается истинным, если Р(х) истинно для каж~

дого элемента х множества X, и ложным в про-

тивном случае.

Говорят, что высказывание х X Р(х) есть ре-

зультат применения квантора всеобщности к преди-

кату Р(х).

Определение 2. Экзистенциальным выска-

зыванием называется выражение х X Р(х) (чита-

ется „существует такой x, принадлежащий X, что

выполнено Р(х)"), которое считается истинным,

если найдется хотя бы один элемент х множества

X, для которого истинно Р(х), и ложным в про-

тивном случае.

Говорят, что высказывание х X Р(х) есть ре-

зультат применения квантора существования к пре-

дикату Р(х).

Пример 1. Пусть А(х) означает предикат ,,х —

рукописная книга", заданный на множестве книг X.

Тогда в результате применения кванторов всеобщ-

ности и существования получим следующие выска-

зывания:

х X А(х), означающее „Все книги рукописные"

(ложь);

х X А (х), означающее „Некоторые книги

рукописные" (истина).

До сих пор мы рассматривали высказывательные

формы, в которые входила только одна переменная.

Обычно такие формы связаны с описанием свойств

элементов множества X. Если же речь идет о задании

соотношений между элементами различных множеств

(или одного и того же множества), то приходится

использовать высказывательные формы, содержащие

несколько переменных. Так, при изучении отношений

на множествах мы столкнулись с понятием бинарной

(двухместной) высказывательной формы. Например:

„читатель х запросил книгу у", „читатель х старше

читателя у", „река х впадает в море у" и т. д. В этих

формах х и у являются свободными переменными,

принимающими значения из множеств X и У.

Над двухместными выскавывательньши формами

также можно проделывать все логические операции

и строить новые формы. Например, при изучении

зависимости читательского спроса от возраста нам

необходимо исследовать сложную форму „читатель

х запросил книгу у", „читатель х старше читателя у"

и т. д. Двухместные высказывательные формы можно

превращать в высказывания путем подстановки кон-

кретных элементов (а, b) из X У. Если же в двух-

местную форму подставить только один элемент, то

она превратится в одноместную высказывательную

фoрму. Например, подставляя х = „Волга" в двух-

местную форму ,,х впадает в море у", мы получим

одноместную форму „Волга впадает в море у".

Применение по каждой из переменных одного из

кванторов также превращает двухместную высказы-

вательную форму в высказывание. При этом кванторы

могут быть как одноименными, так и разноименными.

Сразу же обратим внимание, что одноименные кван-

торы можно менять местами, а разноименные —

нельзя.

Пример 2. Пусть Р(х, у) означает „писатель х

написал книгу у". Тогда применение кванторов поз-

воляет построить следующие высказывания:

Р(х, у) — „Все писатели написали все книги".

Р(х, у) —„Для всех писателей есть книга,

которую они написали".

Р(x, у) — „Существует писатель, написав-

шнй все книги".

Р(x, у) — „Существует писатель, написавший

некоторую книгу".

Второе и третье высказывания, в которых разноимен-

ные кванторы поменялась местами, имеют различный

смысл.

Если к двухместной высказывательной форме при-

менить квантор по одной переменной, то получится

одноместная высказывательная форма относительно

той переменной, которая осталась свободной. Напри-

мер, xP(x, у) означает „Все писатели написали кни-

гу y", a yP(x, у) означает „Писатель х написал

некоторую книгу".

В заключение мы ВЫЯСНИМ важный вопрос построения

отрицания высказываний с кванторами. Начнем с

примера. Задано истинное высказывание „Все люди

смертны". Чтобы убедиться в ложности высказывания

„Не все люди смертны", нужно найти хотя бы одного

бессмертного человека, т. е. должно быть истинным

высказывание „Существует человек, который не смер-

тен". Мы видим, что отрицание высказывания с

квантором всеобщности и предикатом „смертны"

привело нас к высказыванию с квантором существо-

вания и отрицанием предиката „смертны". Докажем

общее утверждение, подсказанное примером.

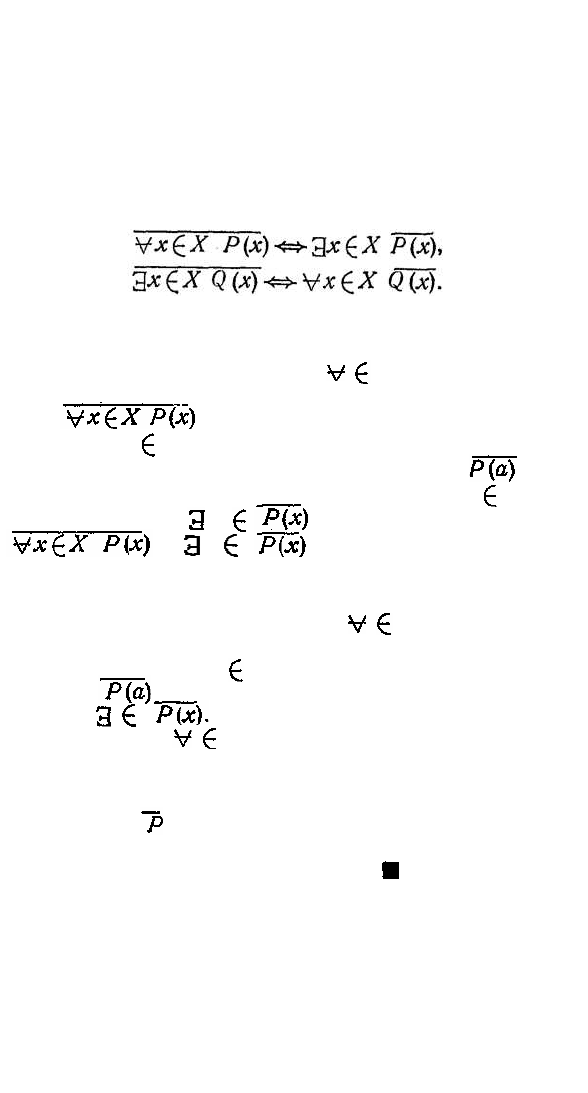
Теорема. Правило отрицания высказываний с

кванторами описывается следующими равносиль-

ностями:

Пусть теперь высказывание х X Р(х) оказалось

ложным. Для этого достаточно, чтобы нашелся хотя

бы один элемент а X, для которого Р(а) ложно.

Но тогда

истинно и таким же является выска-

зывание х X

Так как отрицание ложного

высказывания х X Р{х) истинно, то и во втором

случае выписанные высказывания имеют одинаковые

значения истинности. Поэтому они равносильны.

Для доказательства второй равносильности пере-

обозначим (х) через Q(x), возьмем отрицание

обеих частей первой равносильности и воспользуемся

законом двойного отрицания (АЛ8)

3. Множества истинности. Между множествами и

высказываниями уже не раз отмечалась тесная взаимо-

связь. Сейчас мы изучим эту аналогию более деталь-

но. Введем следующее

Определение 1. Совокупность М

значений

переменной х из множества X, при которых выска-

зывательная форма А(х) истинна, называется мно-

жестеом истинности этой формы.

тогда

ложно. Это означает, что нет

элементов а X, которые не обладали бы свойством

Р(а). Следовательно, свойство

не

выполняется ни для одного элемента а X, т. е.

высказывание

х X ложно. Значит, для

х X

значения истинности в

данном случае совпадают.

Доказательство. Начнем с первой равносиль-

ности. Пусть высказывание х X Р(х) истинно,