Елизаров А.М. Математические методы в библиотечной работе
Подождите немного. Документ загружается.

Т а б л и ц а 1
ситуациях — "х меньше у", „x севернее у", "х — чита-
тель книги у", „запрос х релевантен документу у" —
два объекта х и у находятся в некотором отношении
друг с другом. При этом для некоторых двух объек-
тов эти выделенные свойства выполняются, а для
некоторых — нет. Так, про два пункта на поверхности
Земли имеет смысл говорить, что один севернее
другого (это можно проверить, глядя на карту), тогда
как бессмысленно спрашивать, находится ли Москва
севернее Луны. Кроме того, далеко не всегда х и у
21
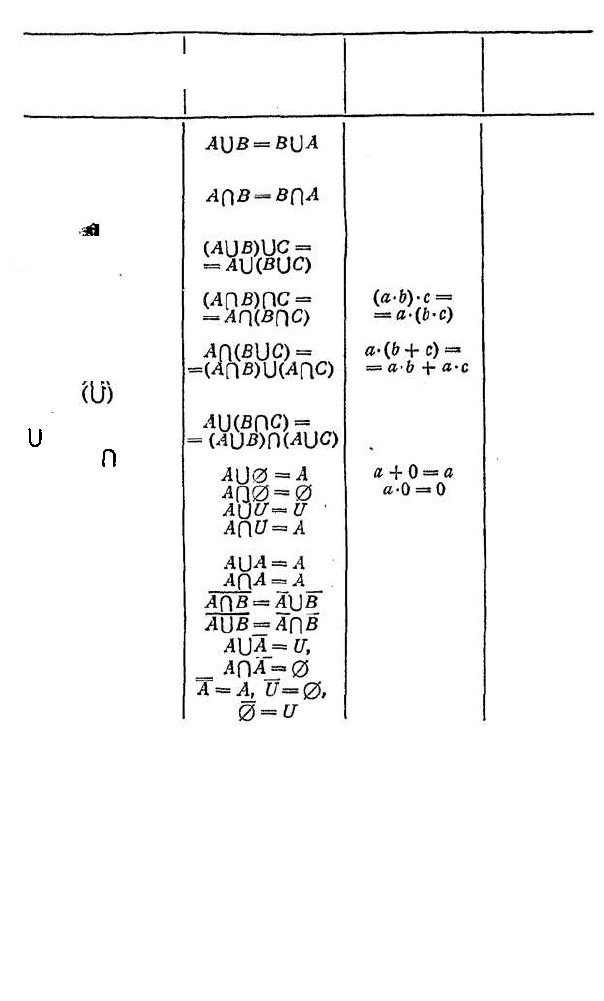
Названи
е
формулы
алгебры
чисел
Формула
алгебры
чисел
Название форму-
лы алгебры
множеств
Формула
алгебры множеств
а + b = b + a
Коммутати
в
-
ность сло-
жения
Коммутатив-
ность умно-
жения
Ассоциатив-
ность сло-
жения
Ассоциатив-
ность умно-
жения
Дистрибу-
тивность (•)
относитель-
но (+)
Свойство
н
у
л
я
К
оммутативность
объединения
Коммутативность
пересечения
Ассоциативность
объединения
Ассоциативность
пересечения
а•b=
b
•a
(
а
+
b
)
+
с
=
=а + (b + с)
Д истрибутивность
(∩) относительно
Дистрибутивность
( ) относительно
(∩)
Свойство пустог
о множества
Свойство универ-
сального множе-
ства
Идемпотентность
Законы де Мор-
гана

можно менять местами. Например, если в случае
отношения "х — читатель книги у" взять x = „Алек-
сандров", а у = „Мастер и Маргарита", то мы получим
разумное утверждение „Александров — читатель книги
„Мастер и Маргарита"", тогда как, выбрав вместо х
элемент у, придем к бессмысленному утверждению.
Поэтому будем в дальнейшем, кроме выбора пары
элементов х и у, отличать порядок следования х, у от
у, х. Иными словами, будем рассматривать
упорядоченные пары элементов. Перейдем к строгим
формулировкам.
Определение 1. Декартовым произведением
множеств А и В (обозначается А Х В) называется
множество всех упорядоченных пар (х, у) таких,
что х — элемент множества А, у — элемент мно-
жества В: АХВ={(х, у)|х А и у В}.
При этом элемент х называется первой, а у —
второй координатой упорядоченной пары.
Пример 1. Пусть А — {Блок; Булгаков; Пушкин},
В = {„Двенадцать"; „Мастер и Маргарита"}. Тогда
декартово произведение множеств А и В состоит из
следующих пар;
АХВ = {(Блок, „Двенадцать"); (Блок, „Мастер и
Маргарита "); (Булгаков, „Двенадцать "); (Булгаков,
„Мастер и Маргарита"); (Пушкин, „Двенадцать");
(Пушкин, „Мастер и Маргарита")}.
Отметим, что для конечных множеств А и В не-
трудно подсчитать число элементов, входящих в
декартово произведение: |АХВ| = |А |•|B|. В дан-
ном примере | A | = 3, |B| = 2, а |АХВ| = 2• 3=6.
Определение 2. Бинарным, отношением R на
множестве A X В называется подмножество R де-
картова произведения АХВ.
Формально отношение мы будем записывать как
пару (А X В, R). Тот факт, что два элемента х, у
находятся в отношении R, обычно записывают в виде
xRy.
Пример 2. Зададим на множестве AХВ из при-
мера 1 несколько отношений. Пусть R
1
— библиогра-
фическое отношение "х написал книгу у". Тогда
R
1
={(Блок, „Двенадцать"); (Булгаков, „Мастер и
Маргарита")}. Пусть R
2
— отношение „х читал книгу
у", тогда это отношение может иметь вид R
2
=
22

= {(Блок, „Двенадцать"); (Булгаков, „Двенадцать");
(Булгаков, „Мастер и Маргарита")}.
Часто встречается случай задания бинарного отно-
шения на декартовом произведении одного и того
же множества М. В этом случае отношение обозна-
чают как (M, R), где М —множество, на котором
задается отношение, а R М X М. Имеется несколько
простейших бинарных отношений, которые выделяют-
ся специальными свойствами.
Определение 3. Отношение (М, М) называется
полным отношением, отношение (М, Ø) — пустым
отношением, а отношение (М, Е), где E = {(x, у) |х =
у} — отношением равенства.
Полное отношение обозначается буквой U и вы-
полняется для всех пар элементов из М; пустое
отношение обозначается Ø и показывает, что ни для
одной пары элементов из М оно не выполнено. Отно-
шение равенства Е означает: хЕу тогда и только
тогда, когда х = у, т. е. х и у — один и тот же эле-
мент множества М.
Рассмотрим один из способов задания отношений,
который приведет нас к важному математическому
понятию.
Пример 3. Пусть М={Ф
1
, Ф
2
, Ф
3
, Ф
4
, Ф
5
}— множество
филиалов централизованной библиотечной системы
(ЦБС), на котором задано отношение „филиал х
передал книгу филиалу у". Изучая это отношение, мы
выясняем спрос на литературу в филиалах ЦБС и пути
ее движения. Вместо тогo, чтобы выписывать все
пары (x, у), в которых указываются филиалы,
передавшие и принявшие книги, занесем в таблицу
данные, отмечая факт передачи книги числом 1, а
отсутствие передачи — числом 0. По ней можно
получить полное представление о запросах
на книгу и о путях ее передачи.
Так, из таблицы 2 видно, что
филиал Ф
1
передал книгу в фи-
лиалы Ф
2
, Ф
5
, но не передавал ее
в филиалы Ф
3
, Ф
4
и т. д. С
аналогичным способом задания
отношений мы сталкиваемся,
например, при знакомстве с
турнирными таблицами сорев-
нований. При этом исходное
23
Таблица 2
множество М составляют команды-участницы, а би-
нарным отношением на М служит отношение "х
победил у".
Такой способ интерпретации называется матрич-
ным, т. к. таблица чисел, состоящая из нескольких
строк и столбцов, называется матрицей. Матричная
интерпретация бинарных отношений осуществляется
следующим образом. Пусть M —множество из n
элементов и R — некоторое отношение на нем. Про-
нумеруем элементы множества М числами от 1 до п
Построим теперь квадратную таблицу (матрицу) раз-
мером n X n. Ее i-я строка соответствует i-му эле-
менту множества М, а j-й столбец —j-му элементу.
На пересечении i-й строки и j-го столбца ставится
элемент a
ij
= 1 (читается ,,а-и-жи"), если выполнено
соотношение x
i
Rx
j
, и 0 — в противном случае. Тогда
общее правило задания матрицы бинарного отноше-
ния примет вид
1, если выполнено x
i
Rx
j
,
0, если не выполнено x
i
RX
j
.
Матрицу, составленную из чисел a
ij
, обычно записы-
вают в виде
Пример 4. Выясним, какими матрицами задаются
полное, пустое отношения и отношение равенства.
По определению, полное отношение U выполняется
для любых двух элементов х
i
, x
j
из M, следовательно, в
этом случае a
ij
= 1 для любых номеров i и j. Матрица,
задающая U, имеет вид |1|. Пустое отношение не
выполняется ни для одной пары элементов х
i
, x
j
,
значит, в этом случае a
ij
= 0 и матрица имеет вид |0|.
Отношение равенства Е выполняется только для двух
совпадающих элементов x
i
и х
j
. Тогда элементы
матрицы, задающей E, имеют вид
Иной способ интерпретации бинарных отношений
связан с геометрическим представлением отношений
на плоскости. Изобразим элементы множества М точ-
ками на плоскости и соединим точки x
i
и x
j
стрел-
24

Рис. 11. Полное отношение, пустое отно-
шение и отношение равенства
ками, если выполнено соотношение х
i
Rх
j
. Если x
i
Rx
i
то у точки x
i
нарисуем петлю, выходящую из х
i
и
входящую в ту же точку. Фигура, составленная из то-
чек и соединяющих стрелок, называется графом, а
соединяющие стрелки — ребрами графа.
Пример 5. Опять обратимся к отношениям U,
Ø, E и нарисуем их графы (рис. 11). Будем считать,
что множество М={х
1
, х
2
, х
3
, х
4
}. В графах полного
отношения и отношения равенства стрелки про-
ведены из вершины x
i
в x
j
и наоборот. В подобных
случаях принято стрелки не обозначать вовсе.
2. Общее понятие о матрицах. При интерпретации
бинарных отношений мы столкнулись с матрицами,
представляющими таблицы чисел, составленные из
нулей и единиц. Понятие матрицы широко применя-
ется в математике и ее приложениях, поэтому мы
более подробно ознакомимся с элементами теории
матриц.
Определение 1. Матрицей порядка mХп на-
вызается прямоугольная таблица, имеющая вид
Здесь а
ij
обозначают какие-нибудь вещественные
числа и называются элементами матрицы. Число т
указывает на количество строк матрицы, a n — на
количество столбцов. Если т = n, то матрицу назы-
вают квадратной. Элементы а
11
, а
22
, ..., а
nn
называют
главной диагональю квадратной матрицы.
Две матрицы, имеющие одинаковые размеры (т. е.
одинаковое число строк и столбцов), называются
25
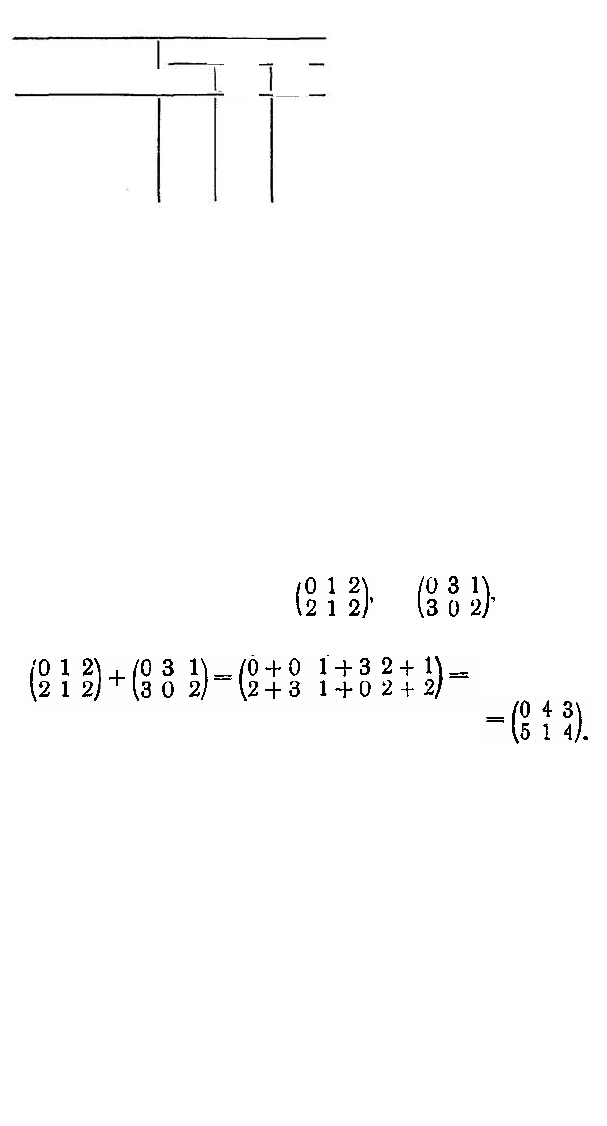
равными
тогда и только
тогда, когда равны их
соответственные
элементы.
Познакомимся с
примером использова-
ния матриц при про-
ведении библиотеко-
ведческих исследова-
ний.
Пример 1. При изучении читательских интересов
полезно составлять матрицу содержания запросов.
Для этого в строку располагают темы или разделы
фонда библиотеки, а в столбец — фамилии читателей. На
пересечении соответствующих строк и столбцов
указывается количество книг (или запросов), заказанных
соответствующими читателями. Получившаяся в
результате матрица отражает содержание запросов
читателей данной библиотеки (табл. 3).
Над матрицами производятся операции» аналогичные
операциям над числами.
Определение 2. Суммой матриц А, В одного
и того же порядна т Х п называется матрица С
(обозначаемая С = А + В), элементы которой получены
путем сложения соответствующих элементов: с
ij
=
= а
ij
+ b
ij
.
Пример 2. Пусть
А
=
В =
тогда
C = A + B =
=
Другой важной операцией является умножение
матриц.
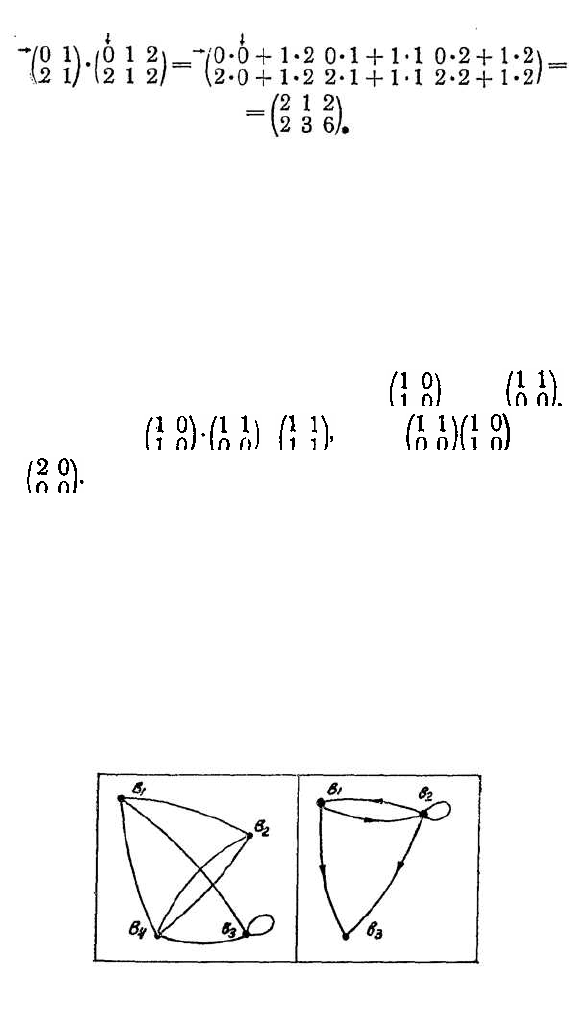
Определение 3. Произведением матрицы А
порядка m X k на матрицу В порядка k X n назы-
вается матрица С порядка т X п (обозначаемая
С = А•В), компоненты которой равны с
ij
= а
ij
b
ij
+
+ a
i2
b
2j
+... +
а
ik
b
kj
.
Обратим внимание, что умножение матрицы
А
на
матрицу
В
возможно только в случае, если число
столбцов матрицы
А
равно числу строк матрицы
В.
В
противном случае операция умножения A на В не-
возможна.
26
Таблица 3
Раздел
Читатель
нп
хл
ОПЛ
Александров
Борисов
Володина
Гришин
Данилов
5
3
1
9
1
3
2
4
2
При этом нужно взять строку» отмеченную → по-
вернуть и приложить в столбцу» помеченному ↓ .
Перемножив соответствующие элементы и сложив их,
мы получим элемент на пересечении строки → и
столбца ↓ . Аналогично поступаем в остальных
случаях.
Наиболее просто перемножать квадратные матри-
цы, однако сразу же предупредим, что произведение
матриц не подчиняется законам умножения для чисел.
Так» вообще говоря, А•В ≠ В•А.
Пример: возьмем матрицы А = и В =
тогда А•В = =
В•А= =
=
Очевидно, что А•В ≠В•А.
Тем не менее, ряд законов алгебры матриц похож
на соответствующие законы алгебры чисел. Например, А
+ В = В + А, А + (В + С) = (А + В) + С, А• (В+С)=
=А•B + А•С, А•(В•С)=(A•В)•С и т. д.
3. Общее понятие о графах. Познакомимся де-
тальнее с математическим объектом, возникшим при
изучении бинарных отношений,— с графом. Представ-
ление связей между элементами с помощью графа —
совокупности точек плоскости и отрезков, соединя-
ющих некоторые из них,— оказывается полезным в
27
Пример 3.
Рис. 12. Граф и орграф

самых различных разделах математики и техники,
физики и биологии, кибернетики и библиотековедения.
Дадим строгие определения.
Определение 1. Графом Г называется пара
<В (Г), Р(Г)>, где В (Г) — непустое конечное множе-
ство элементов, называемых вершинами, а Р(Г) —
конечное множество пар элементов из В (Г) (не
обязательно различных), называемых ребрами.
Обычно говорят, что ребро {х, у} соединяет вершины
х и у. Ребро {х, х}, соединяющее вершину х с ней
самой, называется петлей. Отметим, что в графах
допускается несколько ребер, соединяющих одну и
ту же пару вершин.
Например, на рис. 12 изображен граф, у которого
В ( Г )={b
1
, b
2
, b
3
, b
4
},
а множество ребер
Р ( Г )
состоит из
пар {b
1
, B
2
},
{b
1
, b
3
}, {
b
1
, b
4
}, {b
3
,, b
3
}, {b
2
,
b
4
}, {b
2
, b
4
), {b
3
, b
4
). В
этом графе ребро {b
3
, b
3
} является петлей, а ребро {b
2
,
b
4
} проведено дважды.
Заметим, что в определении графа в качестве ребер
выбирались неупорядоченные (!) пары вершин. Взяв
вместо неупорядоченных пар упорядоченные, мы при-
дем к понятию ориентированного графа.
Определение 2. Ориентированным графом
(или кратко, орграфом) называется пара <В(Г),
С (Г)>, где В (Г)—непустое конечное множестве эле-
ментов, называемых вершинами, а С(Г) — конечное
множество упорядоченных пар элементов из В (Г) (не
обязательно различных), называемых стрелками.
Обычно говорят, что (х, у) является стрелкой из
вершины х в вершину у. Заметим, что стрелки (x
-
, у)
и (у, х) различны. Так, на рис. 12 изображен орграф со
стрелками (b
1
, b
2
), (b
1
, b
3
), (b
2
, b
1
), (b
2
, b
3
) и (b
2
, b
2
).
При изучении графов оказываются полезными
числовые характеристики, связывающие множества
вершин и ребер (или стрелок). Назовем степенью
вершины х (обозначается ст (х)) в графе число ребер,
соединенных с этой вершиной. Если в вершине графа
есть петля, то ребро, образующее эту петлю, под-
считывается дважды. Между числом ребер и степе-
нями вершин графа существует простое соотношение.
Теорема 1. Число ребер графа равно половине
суммы степеней его вершин.
Доказательство. Пусть дан граф Г с верши-
нами b
1
, ..., b
п
, степени которых соответственно
28

равны ст (b
1
), ..., ст (b
n
). Чтобы найти число всех
ребер графа, сосчитаем их в каждой вершине. Оно
равно степени этой вершины ст (b
k
). Сложим все
числа ст(b
k
). Тогда число всех ребер будет равно
половине этой суммы, потому что каждое ребро мы
сосчитаем дважды в тех вершинах, которые оно
соединяет ■.
Для орграфов также имеется подобное утвержде-
ние. Назовем полустепенью исхода вершины х
(обозначается cт(x)) число стрелок орграфа,
имеющих вид (х, у); аналогично
полустепенью
захода вершины х
(обозначается ст(x)) назовем число стрелок орграфа
вида (у, x): Отсюда сразу следует
Теорема 2. Число стрелок орграфа равно сум-
же полустепеней исхода или сумме полустепеней
вахода его вершин.
Пример 1. Пусть Ф
1
, ..., Ф
т
— филиалы ЦБС,
которые обмениваются литературой в процессе об-
служивания читателей. Подсчет обращаемой литера-
туры в сети несложно осуществить, если сформули-
ровать эту задачу на языке теории графов. Для этого
обозначим вершины графа Ф
1
, ..., Ф
т
и соединим Ф
i
и
Ф
j
стрелкой в том случае, когда филиал Ф
i
передал
книгу филиалу Ф
j
. Тогда количество переданных
книг будет равно числу стрелок построенного оргра-
фа, т. е., по теореме 2, сумме полустепеней исхода
(или захода) всех вершин графа. В нашем случае
полустепень исхода (захода) представляет собой коли-
чество книг, переданных (принятых) филиалом, соот-
ветствующим данной вершине. Таким образом, коли-
чество обращаемой литературы в ЦБС равно сумме
книг, передаваемых (или только
принимаемых) филиа-
лами.
Познакомимся еще с одним
важным типом графов.
Определение 3. Двудоль-
ным графом (или орграфом)
называется граф (орграф), вер-
шины которого можно разбить
на два непересекающихся мно-
жества так, что никакие две
вершины из одного и того же
множества не соединены реб-
ром (или стрелкой) (рис. 13).
29
Рис. 13. Двудольный
граф

Отметим, что в двудольном
графе совсем не обязательно каждая
вершина из одного множества
соединена с каждой вершиной
другого множества; если же это
так, то он называется полным
двудольным графом. Если одно
множество вершин состоит из т
элементов, а другое — из п эле-
Рис. 14. Цепь и цикл ментов, то нетрудно проверяется
следующая
Теорема 3. Полный двудоль-
ный граф
с n + m вершинами имеет n m ребер.
С двудольными орграфами мы сталкиваемся при
интерпретации бинарного отношения R, заданного на
декартовом произведении двух множеств А X В. При
этом элементы множеств А и В обозначают вершины
графа, а стрелки, соединяющие эти вершины» прово-
дятся тогда, когда выполнено отношение R между
соответствующими элементами. Например, отношение
R
2
из примера 2 п. 1 характеризует читаемость чита-
телями из множества А литературы, перечисленной
в множестве В. Поэтому отношение R
2
легко пред-
ставить двудольным графом.
Цепью в данном графе с началом b
0
и концом b
п
называется последовательность ребер {b
0
, b
1
}, {b
1
, b
2
},
... , {b
n-1
, b
n
}, в которой все вершины b
0
, b
1
..., b
n
различны (кроме, быть может, b
0
=b
n
). Цепь, у которой
начало и конец совпадают, т. е. b
0
= b
n
, называется
циклом (рис. 14).
Например, {b
0
, b
1
}, {b
1
, b
2
}, {b
2
, b
4
} представляет
собой цепь с началом в вершине b
о
и концом в вер-
шине b
4
. Последовательность ребер {b
о
, b
1
}, {b
1
, b
3
}, {b
3
,
b
2
}, {b
2
, b
4
}, {b
4
, b
0
} является циклом.
Аналогичные понятия определяются и для оргра-
фов, например, орцепью называется последователь-
ность стрелок (b
0
, b
1
), (b
1
, b
2
), ..., (b
n-1
, b
n
) с раз-
личными вершинами.
С помощью введенных выше понятий можно оха-
рактеризовать свойство графа и орграфа состоять из
одного куска. Граф называется связным, если любые
две его вершины можно соединить цепью. Познако-
мимся с одним из наиболее распространенных типов
связанных грав,
vbvмимся с одним из наиболее распространенных типов
связных графов, часто используемым в приложениях.
30
связных графов, часто используемым в приложениях.
