Елизаров А.М. Математические методы в библиотечной работе

Подождите немного. Документ загружается.

Рис. 15. Дерево и лес деревьев

Определение 4. Деревом называется связный

граф, не имеющий циклов. Лесом называется мно-

жество, состоящее из неснольних деревьев.

Например, на рис. 15 изображен лес, состоящий

из четырех деревьев. Деревья представляют простей-

ший тип графов, для которых получено много полез-

ных характеристик. Рассмотрим детальнее способ

построения деревьев. Для этого выберем какую-нибудь

вершину b

. Из нее проведем ребра в соседние вер-

шины b

, b

, ..., из них проведем ребра к их соседям b

, ..., b

, b

, и т. д. Первоначально выбранная

вершина b

называется корнем дерева. Поскольку в

дереве нет циклов, различные цепи, выходящие из

, будут изолированы друг от друга. Каждая цепь

дерева имеет последнее ребро с конечной вершиной,

из которой уже не выходит ни одного нового ребра.

На основании указанного процесса построения де-

ревьев нетрудно устанавливается

Теорема 4. Лес, состоящий из т деревьев и

имеющий п вершин, содержит п — т ребер.

Приведем пример одного из многочисленных при-

ложений понятия дерева.

Пример 2. В библиотечной практике нашли при-

менение информационно-поисковые системы ручного

обращения, реализованные на перфокартах с краевой,

перфорацией. Процесс поиска на перфокартах можно

пре ь как дерево специального вида. Отверстия на

перфокартах дставит разбиты на группы (по 10

отверстий в каждой), которые выделены по тем или

иным признакам. Поэтому при поиске перфокарт по

первому признаку имеется 10 возможностей b

, b

, ...,

, b

; по второму признаку при выполнимости

первого — еще 10 возможностей для каждого

случая: b

, b

..., b

и т. д. Полученное в результате дерево дает

полное редставленне о процессе поиска. Если поиск

осуществляется сразу по нескольким группам призна-

ков, то его можно представить как лес деревьев.

При этом, как показывает результат теоремы 4, сни-

жается число операций, выполняемых при поиске.

4*. Операции над отношениями. Бинарные отно-

шения были введены как подмножества декартова

произведения двух множеств, поэтому над ними мож-

но производить все операции, которые проделывались

над множествами. Тем самым мы получаем возмож-

ность строить новые отношения из уже известных.

Возьмем два отношения R

и R

, заданные на

множестве М (мы рассматриваем этот наиболее рас-

пространенный частный случай). Каждому из них

соответствует некоторое подмножество пар R

ХМ и

MXM.

Определение I. Объединением отношений

называемся отношение, определяемое объ-

единением подмножеств, соответствующих R

и R

Ясно, что отношение х R

y выполняется в том

случае, когда имеет место хотя бы одно из отноше-

ний xR

y или xR

y. На основании этого правила не-

трудно привести интерпретацию операции объединения

отношений с помощью графов: в графе, характери-

зующем объединение отношений, проводятся стрелки,

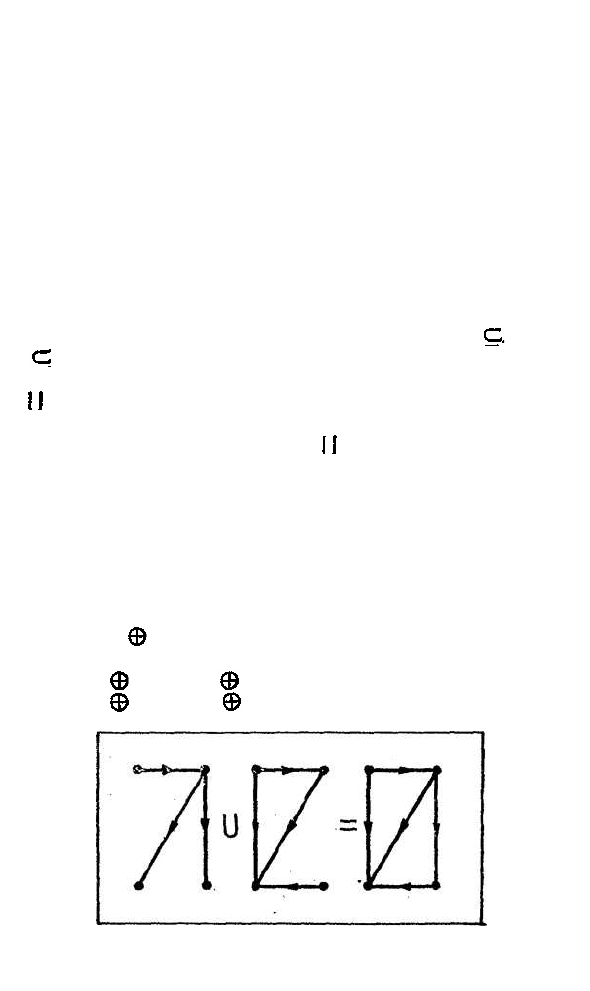
которые имеются хотя бы в одном из графов (рис. 16).

Для матричной интерпретации операции объеди-

нения введем булеву алгебру чисел 0 и 1, в которой

сложение ( ) и умножение (•) определены следую-

щим образом:

0 = 0, 1 0 = 1; 0•0 = 0, 1•0 =0;

0 1 = 1, 1 1 = 1; 0 •1 = 0, 1• 1 = 1.

Рис. 16. Объединение отношений

Пусть отношения R

и R

заданы матрицами

и соответственно. Тогда отношение R

задается

матрицей, элементы которой с

, иными словами,

Пример 1. Ecли R

— отношение „<" на мно-

жестве чисел, а R

— отношение „==", то R

— это

отношение „≤". В самом деле, xR

y означает x<у,

y означает х = у, а вместе эти соотношения дают

х<у или х = у, т. е. x≤y.

Рассмотрим эти отношения на множестве М =

= {1, 2, 3}. Тогда отношения R

и R

заданы матрицами

задается матрицей

Определение 2. Пересечением отношений

∩R

называется отношение, определяемое пере-

селением подмножеств М ХМ, задающих отношения

и R

Соотношение xR

∩ R

y, очевидно, выполнено в тех

случаях, когда одновременно выполнены xR

y и xR

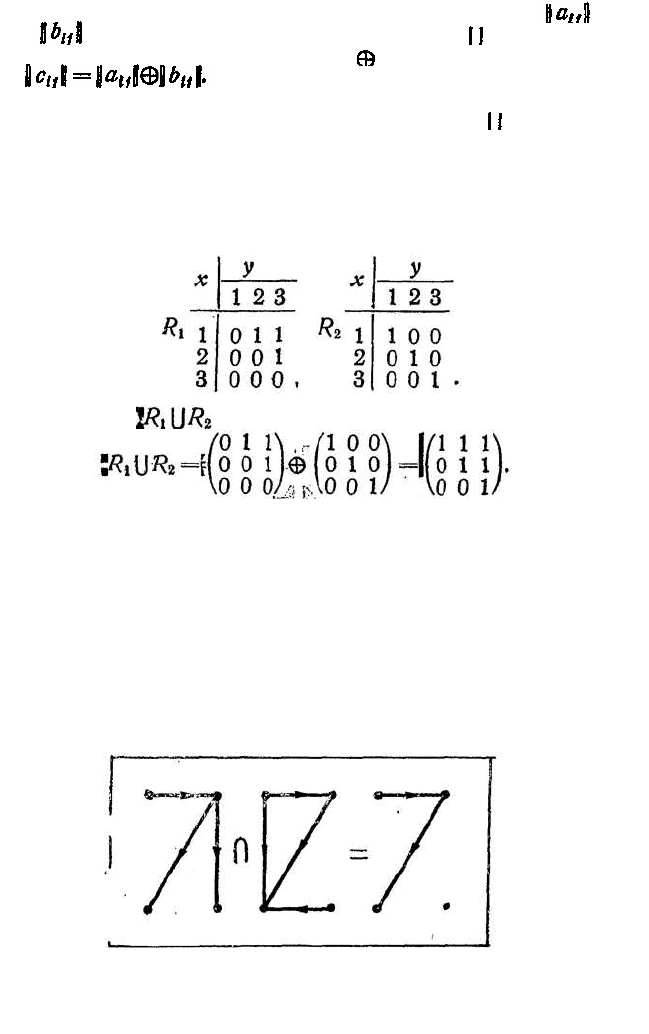
Поэтому граф пересечения отношений содержит лишь

те стрелки, которые соединяют одни и те же верши-

ны в обоих графах (рис. 17). Матрица, задающая пере-

сечение отношений, строится по правилу

Рис. 17. Пересечение отношений

3 Т-743

Отношение

= a

• b

где и —матрицы отношений R

и R

Пример "2. Пусть R

обозначает отношение "<",

а R

— отношение "≠", заданные на множестве чисел.

Тогда R

∩R

есть отношение „<". Рассмотрим эти

отношения на множестве М={1, 2, 3}. Тогда соот-

ветствующие матрицы имеют вид

Для отношений также определено понятие вклю-

чения. Мы будем говорить, что R

включается в R

, и

писать R

, если множество пар, для которых

выполнено отношение R

, содержится во множестве

пар, для которых выполнено отношение R

. Например,

отношение "<" включается в „<". Очевидно, что

для произвольного непустого отношения R можно

записать, что

R U.

Введем еще две операции над отношениями, ко-

торые не сводятся к теоретико-множественным опе-

рациям.

Определение 3. Если R — отношение на мно-

жестве М, то обратное отношение R

-1

(читается

„R в минус первой") определяется условием; xR

-1

тогда и только тогда, когда yRx.

Образно говоря, R

-1

„переставляет" местами x и у

в упорядоченной паре и проверяет выполнимость

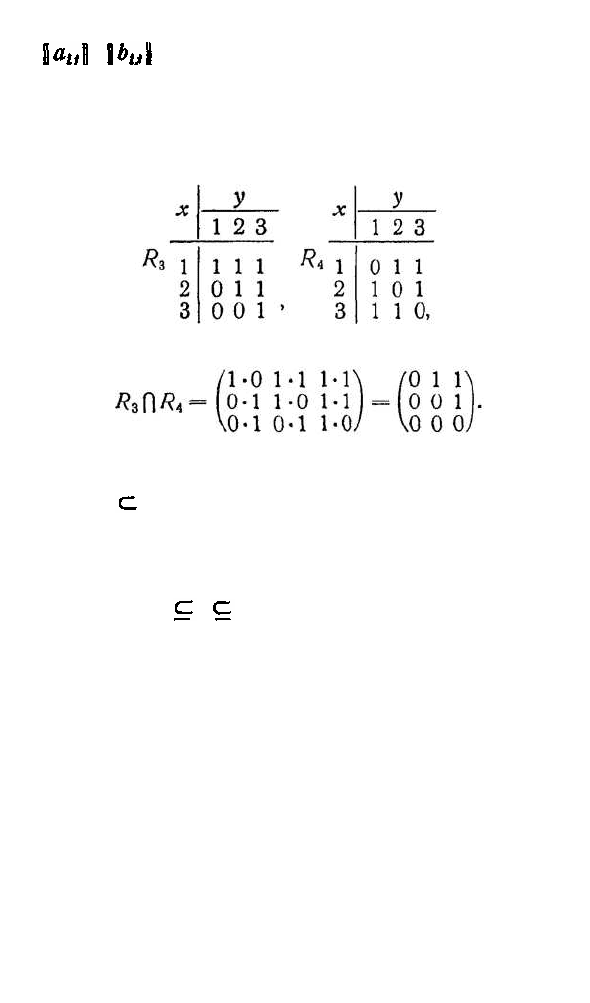
отношения R. При этом граф обратного отношения

отличается от графа исходного отношения тем, что

все стрелки в нем имеют противоположное направле-

ние (рис. 18). Матрица обратного отношения получа-

ется из матрицы исходного отношения путем сим-

метричного отображения элементов относительно

главной диагонали.

а отношение R

∩R

задается матрицей

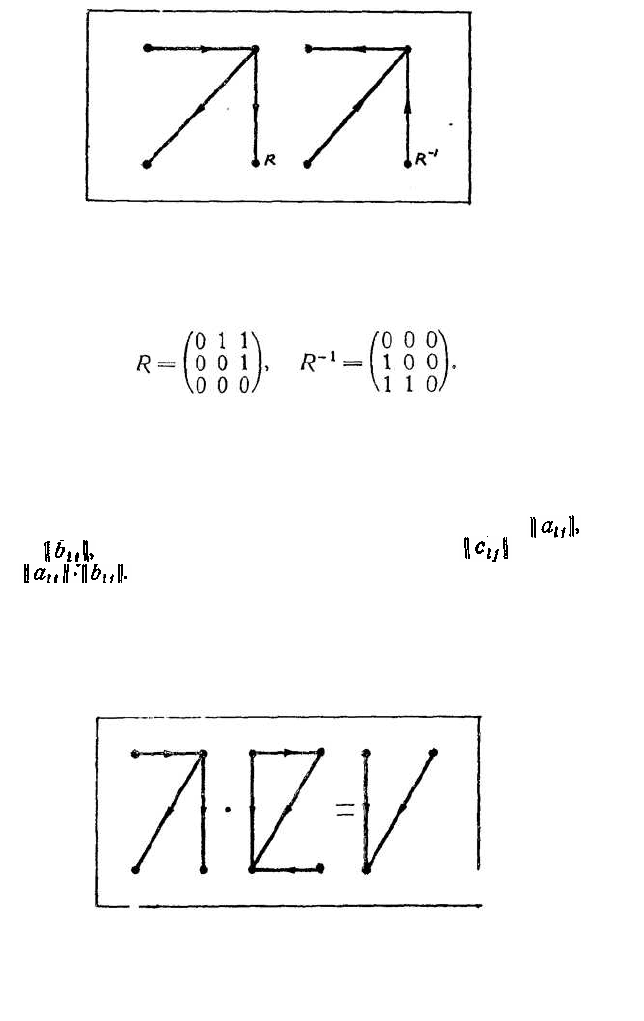
Рис. 18. Обратное отношение

Пример 3. Если R —отношение „<", то R

-1

—

отношение ,,>". Матрицы для отношений R и R

-1

соответственно имеют вид

Определение 4. Произведением двух отноше-

ний R

и R

называется отношение xR

•R

y, которое

выполняется, если существует элемент z такой, что

z и zR

Эта операция на языке матриц интерпретируется

как произведение: если R

задано матрицей

тогда R

•R

задается матрицей =

= Граф произведения отношений строится

следующим образом. Стрелка из вершины х в вер-

шину у проводится в том случае, если найдется

третья вершина z такая, что в графе отношения R

есть стрелка, соединяющая х и z, а в графе отноше-

ния R

— стрелка, соединяющая z и у (рис. 19).

Рис. 19. Произведение отношений

§ 3. Основные типы бинарных отношений

Данный параграф посвящен наиболее распростра-

ненным бинарным отношениям равенства, сходства,

порядка и функциональному отношению. Из всего

многообразия бинарных отношений они выделяются

рядом свойств, к изучению которых мы и обраща-

емся.

1. Свойства отношений. В приведенных ранее при-

мерах бинарных отношений имелось много общего

и в то же время наблюдалось некоторое отличие.

Например, отношения

х равен у (на множестве чисел),

х синоним у (на множестве слов),

х родственник у (на множестве людей)

очень похожи друг на друга, но не похожи на отно-

шения.

х больше у (на множестве чисел), х

род—вид у (на множестве слов), х

старше у (на множестве людей),

которые в свою очередь сходны между собой,

Отвлечение от частностей и конкретного содер-

жания приведенных отношений приводит нас к выде-

лению свойств, характерных для первой или второй

группы.

Определение 1. R называется рефлексивным

отношением на множестве М, если для любого эле-

мента х М выполнено xRx. Иными словами, реф-

лексивное отношение выполняется между элемен-

том и им самим.

Ясно, что отношения равенства или синонимии

рефлексивны, тогда как отношения „больше" или

,,старше" этим свойством не обладают. Если построить

граф рефлексивного отношения, то в каждой его вер-

шине будет проведена петля (рис. 20). В матрице реф-

лексивного отношения на главной диагонали стоят

единицы.

Определение 2. Отношение R называется

антирефлексивным, если из xRy следует х≠ у.

Примерами антирефлексивных отношений могут

служить отножения „род—вид" или „больше".

Рис. 20. Рефлексивное и антирефлексивное

отношения

В графе антирефлексивного отношения петли в вер-

шинах обязательно отсутствуют (рис. 20), а матрица

имеет на главной диагонали нули.

Определение 3. Отношение R называется сим-

метричным, если из xRy следует, что также и yRx.

Например, отношения синонимии или равенства

являются симметричными, В самом деле, если слово x

синоним слову у, то у также синоним для x. Свойство

х = у выполняется для чисел х и у вместе со свой-

ством у = х.

Граф симметричного отношения вместе с каждой

стрелкой» идущей от вершины x

к вершине x

со-

держит стрелку, идущую от вершины x

к вершине х

(рис. 21). В матрице, задающей симметричное отноше-

ние, элементы, симметрично расположенные относи-

тельно главной диагонали, равны между собой.

Определение 4. Отношение R называется

антисимметричным, если из двух соотношений xRy

и yRx выполняется только одно.

Рис. 21. Симметричное и транзитивное

отношени

Отношения „больше" и „старше"— примеры анти-

симметричных отношений. Их графы содержат стрелки

лишь из одних вершин в другие, но не допускают

стрелок, проведенных в обратном направлении.

Наконец, приведем определение последнего рас-

сматриваемого нами свойства бинарных отношений.

Определение 5. R навивается транзитивным

отношением на множестве М, если для любых трех

элементов х, у и z множества M uз того, что xRy

и yRz, следует xRz.

Все отношения, приведенные ранее в примерах,

обладают этим свойством. Например, пусть слово х

синонимично слову у, а слово у синонимично слову z.

Тогда, очевидно, слово х является синонимом и для z,

что доказывает транзитивность отношения синонимии.

Примером нетранзитивного отношения может слу-

жить сходство слов. Будем говорить, что ,,х сходно у",

если слова х и у состоят из одного и того же числа

букв и отличаются лишь одной буквой. Так, мука

сходно мура, мура сходно мера, но уже неверно,

что мука сходно мера — различие в две буквы!

Отличительной особенностью графа транзитивного

отношения является то обстоятельство, что наряду

со стрелками, соединяющими вершины х и у, у и z,

обязательно имеется стрелка, идущая из вершины х

в вершину z (рис. 21).

2. Равенство. Мы переходим к изучению основных

бинарных отношений, которые обладают одновремен-

но несколькими свойствами, описанными ранее.

Определение 1. Отношение R на множестве М

называется равенством (или эквивалентностью),

если оно рефлексивно, симметрично и транзитивно.

Отношение равенства ,,х = у", заданное на множестве

чисел, обладает всеми перечисленными в определении

1 свойствами и, следовательно, является отношением

эквивалентности. Другим примером эквивалентности

является отношение синонимии.

Граф отношения эквивалентности обладает всеми

характерными особенностями для рефлексивных, сим-

метричных и транзитивных отношений: в каждой вер-

шине имеется петля; он состоит из ребер, т. е. стрелки

проведены в обе стороны; вместе с ребрами, соеди-

няющими вершины х, у и у, z, в графе имеются ребра,

соединяющие вершины х и z (рис. 22).

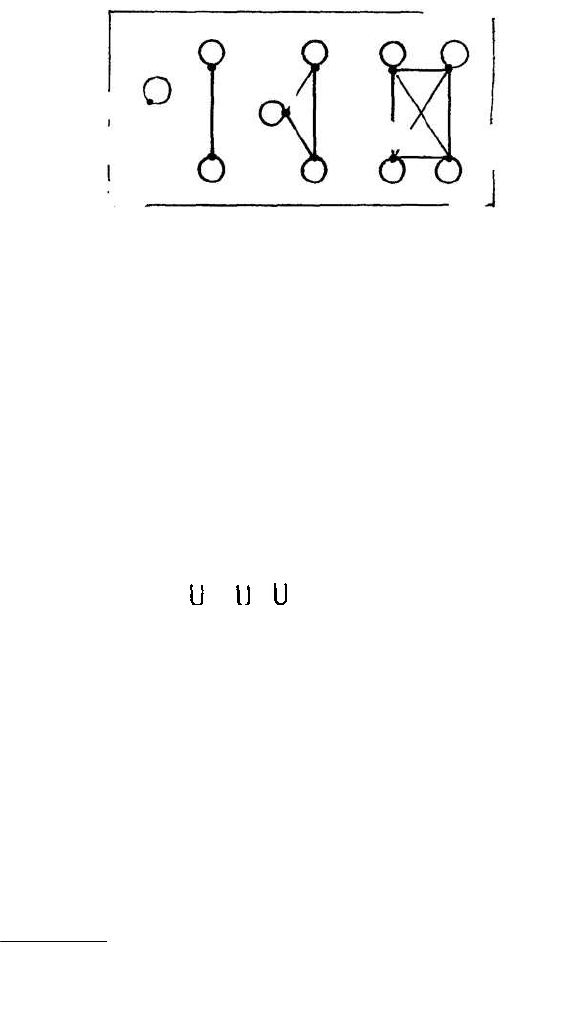
Рис. 22. Графы эквивалентности

Матрица для эквивалентности симметрична, на ее

главной диагонали стоят единицы.

Понятие эквивалентности лежит в основе важного

для библиографическoй деятельности процесса клас-

cификации. Под классификацией понимается „деление

понятий (классов) по одному основанию таким обра-

зом, чтобы получаемые в результате деления под-

классы исключали друг друга" *. Это означает, что

множество понятий М разбито на систему подмно-

жеств (классов) {М

..., М

), которая характеризуется

следующими свойствами:

К1. Ни одно из M

не пусто, М

≠Ø , k = 1,... ,n;

К2. Для различных k и l множества M

и М

не

пересекаются; M

∩M

=Ø, k≠ l;

КЗ. Объединение всех подмножеств из системы

составляет М: М

1 M2

... М

= М.

Определение 2. Система подмножеств из М,

удовлетворяющая свойством (К1) —(КЗ), называется

разбиением множества М.

Оказывается, что задание на множестве М отно-

шения эквивалентности порождает разбиение М на

классы, а разбиению множества на классы соответ-

ствует некоторое отношение эквивалентности. Напри-

мер, отношение синонимии на множестве слов раз-

бивает это множество на классу синонимов. Дадим

строгую формулировку этого свойства.

Теорема 1. Отношение эквивалентности R

на

множестве М определяет разбиение М на классы,

такие, что xR

y сыполнено в том или только в том

случае, когда х и у принадлежат общему классу.

________

.* Черный А. И. Введение в теорию информационного поиска.-

М.: Наука, 1975, с. 37.

На доказательстве теоремы 1 не останавливаемся.

Отношение синонимии, разбивающее множество

слов на классы синонимов,— не единственное отно-

шение эквивалентности, которое можно определить

на этом множестве.

Пример 1. Зададим на множестве слов отноше-

ние ,,х грамматически эквивалентно у", которое счи-

тается выполненным, если после замены слова х на

слово у из грамматически правильной фразы русского

языка вновь получается грамматически правильная

фраза. С помощью этого отношения в русском языке

выделяются лексико-грамматические классы (части

речи). Например, взяв фразу „Свеча горела на столе,

свеча горела" и х = „свеча", объединим в один лек-сико-

грамматический класс (существительные женского

рода) слова, при подстановке которых вместо х

получаются грамматически правильные предложения

русского языка:

Свеча горела на столе, свеча горела

Лучина...

Спичка ...

Луна...

Банка...

Здесь мы следили лишь за грамматической (!) пра-

вильностью фразы. Если же требовать при замене

слов сохранения смысла (семантической правильности),

то мы придем к выделению лексико-семантических

классов, которые играют важную роль в теории инфор-

мационного поиска. Эти классы задаются отношением

„х семантически эквивалентно у", которое выполня-

ется, если замена слова х на слово у не нарушает

смысловой правильности предложения.

3. Сходство. Отношение эквивалентности, обсуж-

давшееся выше, в некотором смысле описывало оди-

наковость эквивалентных элементов, их взаимозаме-

няемость без всяких потерь. Однако далеко не все

объекты равноценны и взаимозаменяемы. Широко

распространена и такая ситуация, когда объекты

лишь похожи друг на друга и замена одного на

другой возможна с некоторыми потерями (разрешае-

мыми в данной ситуации). В этом случае, конечно,

объекты будут похожи сами на себя, и если объект х

похож на у, то у также похож на х. Чем же отли-