Елизаров А.М. Математические методы в библиотечной работе

Подождите немного. Документ загружается.

чается понятие сходства от экви

валентности? Из примера отноше-

ния сходства между словами мы

видели, что транзитивность не

свойственна этому отношению,

поэтому естественным будет сле-

дующее

Определение. Отношение R

на множестве М называется

сходством (или толерант-

ностью), если оно рефлексивно

и симметрично.

Граф отношения сходства характеризуется нали-

чием петель в каждой вершине и стрелками, прове-

денными в обе стороны (рис. 23). Матрица для сход-

ства симметрична, на ее главной диагонали стоят

единицы.

Сходство от эквивалентности отличается тем, что

теперь уже нельзя разбить все объекты на классы,

внутри которых объекты похожи, а между объектами

разных классов сходства нет. В случае сходства воз-

никает ситуация, когда нет четких границ и переход

от одного класса к другому осуществляется последо-

вательным накоплением и (или) потерей некоторых

свойств.

Пример 1. Рассмотрим множество М и все его

непустые подмножества. Два множества А, В из М

назовем сходными друг другу (обозначим AR

B),

если А∩В≠ Ø. Проверим, что введенное таким обра-

зом отношение является сходством на М.

Ясно» что отношение R

рефлексивно, ибо A∩A=

= А≠Ø. Симметричность R

также очевидна в силу

коммутативности, операции пересечения: AR

B, тогда

Ø ≠ А∩В = В∩А ≠ Ø, тогда BR

A. Отметим, что

введенное отношение сходства множеств не тран-

зитивно. Например, пусть А = {1,2,3}, В={3, 4, 5},

С={5,6,7}. Тогда AR

B, т.к. А∩В = {3}; BR

C, т. к.

В∩С={5}, но множество А не сходно С, т.к.

A∩C=Ø.

Пример 2. В процессе информационного поиска

приходится устанавливать релевантность читатель-

скому запросу выдаваемых документов. Для этого

запрос представляют в виде множества дескрипторов,

(т. е. составляют поисковый образ запроса — ПО3),

Рис.

. Гра

сход-

ства

а документ также описывают опре-

деленными наборами дескрипто-

ров, множество которых состав-

ляет поисковый образ документа—

ПОД. Затем, сравнивая ПОЗ и

ПОД, выдают документы, для ко-

торых ПОД∩ПОЗ≠Ø, и назы-

вают их релевантными данному

запросу. Из предыдущего примера

Рис. 24. Граф стро- ясно, что отношение релевантности

гого порядка на множестве дескрипторов явля-

ется сходством, но не эквивалентностью.

4. Порядок. Это отношение возникает при выде-

лении общих свойств, характерных для примеров

второй группы из п.1.

Определение 1. Отношение R на множестве М

называется строгим порядком, если оно антиреф-

лексивно и транзитивно.

Примерами строгого порядка могут служить отно-

шения „больше", „старше", родо-видовое отношение и

т. д.

В графе отношения строгого порядка отсутствуют

петли (рис. 24), а в матрице на главной диагонали

стоят нули. Более того, граф строгого порядка не

содержит циклов, т. е. отсутствуют последователь-

йости вершин х

, х

, …, х

, соединенные ребрами,

такие, что х

=х

. Убедимся в этом.

Теорема. Если R — отношение строгого поряд-

ка, то оно антисимметрично.

Доказательство. Предположим противное.

Пусть нашлись два таких элемента х, у из множества М,

что одновременно xRy и yRx. В силу транзитивности

строгого порядка R отсюда следует, что xRx. Но это

противоречит антирефлексивности отношения R, сле-

довательно, предположение о том, что R не является

антисимметричным, неправильно ■. Из доказанной

теоремы непосредственно следует утверждение о том,

что граф строгого порядка не имеет циклов.

Множество, на котором задано отношение строгого

порядка, называют упорядоченным множеством. На-

пример, множество N натуральных чисел с заданным

отношением „<" является упорядоченным множеством.

Определение 2. Отношение строгого поряд-

на R называется совершенным строгим порядком,

если для всякой пары несовпадающих элементов

х и у из М выполняется либо xRy, либо yRx.

По доказанной выше теореме оба эти свойства не

могут выполняться одновременно, поэтому все пары

из М М разбиваются на три класса: класс пар (х, x);

класс пар (х, у) таких, что xRy; класс пар (х, у) таких, что

yRx.

Примерами совершенного строгого порядка могут

служить отношения „больше", лексикографического

порядка на множестве словарных статей в энцикло-

педии и т. д.

Пример 1. Алфавитный каталог представляет

собой картотеку библиографических описаний, рас-

ставленную по алфавитному принципу: сначала фами-

лии, начинающиеся на А, затем на Б и т. д. С нашей

точки зрения, алфавитный каталог — это множество

фамилий авторов, на котором задано отношение лек-

сикографического порядка.

Однако далеко не во всяком множестве можно

задать естественное отношение совершенного строгого

порядка. Например, на множестве всех подмножеств

из М отношение включения не является совершенным

строгим порядком, т. к. существуют подмножества

из М, которые не включаются одно в другое. Наибо-

лее интересный случай такого частичного строгого

порядка — так называемый древесный порядок.

Определение 3. Отношение строгого порядка

R на М называется древесным порядком, если:

1) из того, что xRy и xRz, следует, что либо

yRz, либо zRy;

2) в М существует максимальный элемент x

та

кой, что для любого x М выполнено xRx

Первое условие этого определения означает, что

для всех элементов, предшествующих х, исходный

древесный порядок превращается в совершенный по-

рядок. Второе условие означает наличие элемента,

которому все подчинены.

Граф отношения древесного порядка является

деревом (рис. 25).

Пример 2. Рассмотрим множество рубрик Уни-

версальной десятичной классификации (УДК) и зада-

дим на нем древесный порядок: xRy, если рубрика х

(д. п.)

Рис. 25. Древесный порядок и граф-схема

УДК

содержит у в качестве подрубрики. Тогда все мно-

жество рубрик УДК превратится в частично упоря-

доченное множество, представляющее из себя лес

деревьев. Например, выберем рубрики, начинающиеся

с цифр 5и 7. Тогда примером упорядочения будет

дерево, изображенное на рис. 25. При этом деревья

с максимальными элементами 5 и 7 не связаны друг

с другом. Аналогичные деревья можно выстроить

и для остальных разделов УДК. В совокупности они

образуют лес деревьев, дающий полное представление

о взаимосвязи рубрик УДК.

5. Функция. С понятием функции знакомятся еще

в школе. Оказывается, функция — это тоже частный

тип бинарного отношения.

Определение 1. Отношение R на множестве М

называется функциональным отношением (сокра-

щенно—функцией), если для всякого элемента х М

существует не более одного элемента у М, для

которого справедливо соотношение xRy.

Элемент х называется аргументом функции, а эле-

мент у, соответствующий элементу х, называется зна-

чением функции R на элементе х. Эта зависимость

по традиции обозначается как у = R (х). Иногда гово-

рят, что у—образ х, а х—прообраз у при отображе-

нии функцией R.

Синонимами слова „функция" в математике явля-

ются „отображение", „оператор", „соответствие",

„преобразование", „функционал".

Пример 1. Рассмотрим несколько отношений,

заданных на множестве М = {1,2,3} (рис.26). Здесь

f и g — функции, a h функцией не является, т.к.

элементу х = 2 соответствуют два (!) разных значе-

ния у = 2 и у = 3.

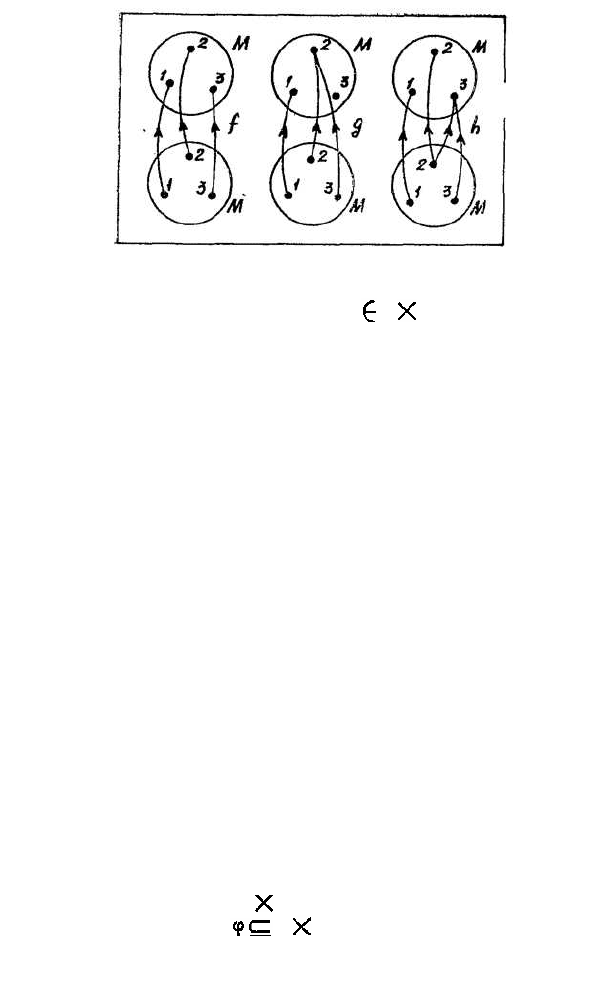
Рис. 26.

Множество всех пар (х, у) М М, для которых

выполнено соотношение xRy, называют графиком

отношения R. Как правило, графики функций изобра-

жают в случае задания функций на бесконечных мно-

жествах.

Пример 2. Если М = R, a R есть отношение ра-

венства Е, то график функции у = E(x), или, как

принято обозначать, у=х представляет из себя бис-

сектрису первого и третьего координатных углов.

Существует несколько способов задания функции

связанных с различной интерпретацией бинарных .

отношений:

1) с помощью таблицы 4 где

указываются все пары (х, у), для Таблица 4

которых выполнено соотношение xRy -------------------

(в данном случае R = Е); x | 1 | 2 | 3...

2) с помощью формулы y = R(x) -------------------

(в данном случае у = х); y | 1 | 2 | 3...

3) с помощью графика.

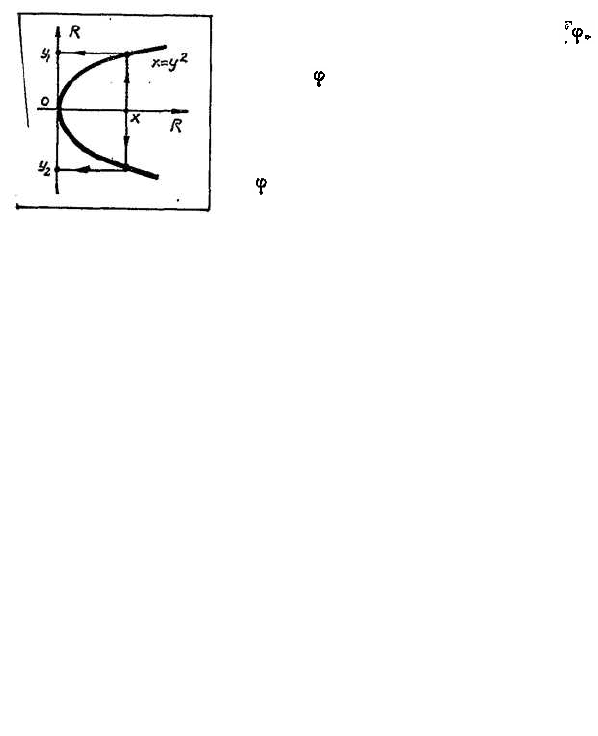
Последний характерен тем, что любая прямая,

параллельная оси Оу, пересечет график функции не

более, чем в одной точке. В то же время график

отношения R = {(x, у) | х = у

} показывает, что это

отношение не является функцией, т. к. любому неот-

рицательному числу х соответствуют два числа у

и —у такие, что у

= (— y)

= x (рис. 27).

Функциональные отношения задают и на декарто-

вом произведении М N двух различных множеств.

При этом функцию М N называют отображением

множества М в множество N, а сами множества М

и N— областью определения и

областью значений функции

Обозначают этот факт следующим

образом: :М→N.

Весьма важным для дальней-

шего является понятие взаимно-

однозначной функции.

Определение 2. Функция

:М→N называется взаимно-

однозначной, если различные эле-

менты множества М отобража-

ются в различные элементы мно-

жества N и любой элемент у

из N имеет прообраз в множестве М.

Рассмотренная в примере 1 функция f является

взаимно-однозначной, а функция g — нет, т. к. разные

элементы х=2 и х=3 отображаются ею в один и тот

же элемент у = 2.

Введенное понятие позволяет нам дать точное

определение понятия эквивалентности двух множеств

(см. п. 1 § 1).

Определение 3. Два множества М и N назы-

ваются эквивалентными или равиомощиыми, если

существует взаимно-однозначная функция, отобра-

жающая одно множество на другое.

Это определение применимо как для конечных,

так и для бесконечных множеств. Заметим, что мно-

жества, эквивалентные множеству N натуральных чи-

сел, называются счетными, а бесконечные множества,

не эквивалентные множеству N, называются несчет-

ными. Первой содержательной теоремой теории мно-

жеств была доказанная Г. Кантором неэквивалентность

множеств N и R, т. е. несчетность множества веще-

ственных чисел.

Рис.

7. Гра

ик отно-

шени

ГЛАВA II

МАТЕМАТИЧЕСКАЯ ЛОГИКА

И ЕЕ ПРИМЕНЕНИЕ В

БИБЛИОТЕЧНОЙ РАБОТЕ

§ 4. Исчисление высказываний

Раздел логики, с которым мы начинаем знаком-

ство, посвящен изучению связей между высказыва-

ниями (каким oбразом одни высказывания строятся

иа других посредством простейших логических опе-

раций).

1. Основные понятия. Мы воспринимаем высказы-

вания через выражающие их повествовательные

предложения русского языка. Высказывания суть

смысл этих предложений. При этом мы не отождеств-

ляем их с предложениями, т. к. одно и то же выска-

зывание можно изложить по-разному. Например,

фразы „Читатель Александров взял в библиотеке

книгу Булгакова" и „Книгу Булгакова взял в библио-

теке для чтения Александров" представляют одно и

то же высказывание, тогда как предложение „Чита-

тель Александров не взял книгу Блока" отражает

нечто другое. В исчислении высказываний различают

лишь высказывания, имеющие разный смысл, а не

высказывания, представленные различными предложе-

ниями. Мы будем предполагать, что встречающиеся

нам высказывания можно отличать друг от друга.

Многие повествовательные предложения, кроме

того, носят многозначный характер, поэтому нельзя

сказать, правильны или нет соответствующие выска-

зывания. Например, про фразы „Сумма чисел 2 и 6

больше 8", „Марс дальше от Солнца, чем Венера",

„Блок написал поэму „Двенадцать" можно сказать,

правильны они или нет, а о высказывании „В нашей

Галактике есть внеземные цивилизации" сейчас мы

этого сказать не можем. В исчислении высказываний

такие предложения не рассматриваются.

Определение 1. Под высказыванием понима-

ется повествовательное предложение, которое мо-

жет быть классифицировано либо как истинное,

либо как ложное (но не как то и другое вместе).

Тем самым из множества всевозможных предложений

русского языка выделяются истинные и ложные

высказывания. Слова „истина" и „ложь", которые

приписывают высказыванию, называются значениями

истинности. Мы будем кратко обозначать их ,,и" и

,,л".

Некоторые высказывания можно разложить на

отдельные части так, что каждая из атих частей будет

самостоятельным высказыванием. Например, высказы-

вание „Александров взял книгу Блока, а Борисов

попросил книгу Булгакова" состоит из двух частей;

„Александров взял книгу Блока" и „Борисов попро-

сил книгу Булгакова".

Определение 2. Высказывание, которое можно

разложитъ на части, также являющиеся высказы-

ваниями, называется сложным, а неразложимое

высказывание — простым.

Основная задача исчисления высказываний — опре-

делить, как зависит истинность сложного высказыва-

ния, построенного при помощи логических операций

из простых, если известно, ложными или истинными

являются эти простые высказывания.

2. Логические операции. Для конструирования из

простых высказываний сложных применяют пять ос-

новных логических операций.

Определение 1. Отрщанием высказывания А

называют такое высказывание В, что В ложно,

когда А истинно, и В истинно, если А ложно.

Отрицание высказывания А обознача-

ют Ā (читается „не А" или „неверно, что Таблица 5

А"). Занесем данные в таблицу, называе- Отрицание

мую таблицей истинности (табл. 5).

По ней можно получить всю нужную

информацию об операции отрицания.

Определение 2. Конъюнкцией (ло-

гическим умножением) высказываний А, В

называется сложное высказывание A/\B

(читается „А и В"), истинное лишь в том случае,

когда оба высказывания истинны. Если же хотя бы

одно из них ложно, mo сложное высказывание А/\В

считают ложным (табл. 6). В лингвистике эта

операция характеризуется союзом „и", соединяющим

два предложе-

ния. Например, высказывание „Алек- Таблица 6

сандров взял книгу Булгакова и не

Конъюкция

взял книгу Блока" является конъюнк-

цией двух высказываний. Заметим, что ----------------

в русском языке в подобных случаях А | B | A /\ B

подлежащее дважды не повторяют но -----------------

подразумевают.

Высказывания можно связать друг с и | и | и

другом не только союзом „и", но и и | л | л

союзом „или". Например, „Александров л | и | л

взял книгу Булгакова или Пушкина". л | л | л

В повседневной речи союз „или" имеет два различ-

ных значения — разделительное и неразделительное.

В приведенном примере читатель может взять ту

или иную книгу, а может быть, и обе — здесь „или"

имеет неразделительное значение. Однако в предло-

жении „Борисов учится в Москве или Казани" подра-

зумевается, что выполняется только одна из возмож-

ностей— здесь союз „или" имеет разделительное

значение. Чтобы устранить эту неопределенность, в

исчислении высказываний условились использовать

лишь неразделительное „или".

Определение 3. Дизъюнкцией (логическим

сложением) высказываний А, В называется сложное

высказывание А В (читается „А или В"), истинное,

если хотя бы одно из этих высказываний истинно,

и ложное лишь в том случае, когда ложны оба

высказывания (табл. 7).

Рассуждения чаще всего представляют

собой цепочки высказываний и носят

условный характер, т. е. утверждают, что

некоторое высказывание истинно в

предположении истинности другого

высказывания. Например: „Если мы

рассмотрим настоящее время, то налицо

информационный взрыв". В общем виде

такие высказывания записываются как

„Если истинно А, то истинно В", или,

короче, „Если А, то В". В исчислении

высказываний также есть операция,

описывающая подобную ситуацию.

Определение 4. Импликацией высказываний

А, В называемся сложное высказывание А→В

4 Т-743

Таблица 7.

Дизъюнкция

А\/В

и и

л и

(читается

если A, то В"), ложное лить в том

случае, когда А истинно, а В ложно (табл. 8).

Высказывание А называют условием, а В—заклю-

чением. Импликация с ложным условием считается

истинной как при истинном, так при ложном заклю-

чении. Говорят, что такая импликация

истинна тривиальным образом. Пример:

„Если Александров придет в библиотеку,

то он выберет себе книгу Булгакова". Но

если читатель не пришел в библиотеку,

можно ли утверждать, что наше

высказывание неверно? Конечно нет.

Определение 5. Эквиваленци-

ей высказываний, А, В называется,

сложное высказывание А←→В (читается

„А тогда и только тогда, когда В"),

истинное в том и только том случае, когда одно-

временно истинны или ложны оба высказывания

(табл. 9).

Примером эквиваленции двух выска-

зываний может служить предложение

„Множество М равно множеству N

тогда и только тогда, когда выполнены

включения М

N М".

Теперь после введения операций,

позволяющих из простых высказываний

строить новые, более сложные, мы

обратимся к задаче определения зна-

чений истинности сложных высказываний

по известным значениям истинности

простых высказываний. Прежде всего условимся о

порядке выполнения логических операций: сначала

выполняется операция отрицания —, затем

затем

затем → и, в последнюю очередь, ←→. Это

соглашение позволяет_ сокращать запись, например,

формула А В→С←→Ċ\/A является краткой записью

сложного высказывания ((А В)←→((С)

). Буквы,

обозначающие произвольные высказывания, будем

называть логическими переменными.

Если составить из логических переменных выра-

жение, связав их по определенным правилам логи-

ческими операциями, то получится сложное выска-

зывание, которое при одних значениях переменных

Тaблица 8

Импликация

А В А→В

и и

и л

Таблица 9

Эквиваленция

А←→В

и и

и л л