Елесин В.Ф., Кашурников В.А. Физика фазовых переходов
Подождите немного. Документ загружается.


ɥɟɧɢɹ. Ɋɚɫɫɦɨɬɪɢɦ ɝɚɡ ɱɚɫɬɢɰ ɫ ɫɢɦɦɟɬɪɢɱɧɨɣ ɜɨɥɧɨɜɨɣ ɮɭɧɤ-
ɰɢɟɣ, ɨɩɢɫɵɜɚɟɦɵɯ ɜɨ ɜɬɨɪɢɱɧɨɦ ɤɜɚɧɬɨɜɚɧɢɢ ɨɩɟɪɚɬɨɪɚɦɢ
ɪɨɠɞɟɧɢɹ a
+
ɢ ɭɧɢɱɬɨɠɟɧɢɹ a ɢ ɩɨɞɱɢɧɹɸɳɢɯɫɹ ɫɥɟɞɭɸɳɢɦ
ɤɨɦɦɭɬɚɰɢɨɧɧɵɦ ɫɨɨɬɧɨɲɟɧɢɹɦ (Ȼɨɡɟ):
aa aa aa aa aa aa
kk kk kk kk kk kk kk'' ' '' ''
,,
G
00. (9.1)
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɜ ɨɬɥɢɱɢɟ ɨɬ ɮɟɪɦɢɨɧɨɜ ɜɨɥɧɨɜɚɹ
ɮɭɧɤɰɢɹ ɫɢɦɦɟɬɪɢɱɧɚ ɩɨ ɩɟɪɟɫɬɚɧɨɜɤɚɦ ɤɨɨɪɞɢɧɚɬ (ɢɢɦɩɭɥɶ-
ɫɨɜ) ɱɚɫɬɢɰ. ɇɚ ɜɨɥɧɨɜɭɸ ɮɭɧɤɰɢɸ ɜ ɩɪɟɞɫɬɚɜɥɟɧɢɢ ɱɢɫɟɥ
ɡɚɩɨɥɧɟɧɢɹ |n
k1
....n
kN
>, ɝɞɟ n
ki
- ɱɢɫɥɚ ɡɚɩɨɥɧɟɧɢɹ ɜ ɫɨɫɬɨɹɧɢɢ
ɫ ɢɦɩɭɥɶɫɨɦ k
i
, ɨɧɢ ɞɟɣɫɬɜɭɸɬ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ
an nn an n n aan nn
kk kk kk k k kkk kk
||,| |,||! ! ! ! !
!
111 . (9.2)
ɑɢɫɥɚ ɡɚɩɨɥɧɟɧɢɹ ɤɜɚɧɬɨɜɵɯ ɫɨɫɬɨɹɧɢɣ ɩɪɢ ɫɢɦɦɟɬ-
ɪɢɱɧɵɯ ɜɨɥɧɨɜɵɯ ɮɭɧɤɰɢɹɯ ɧɢɱɟɦ ɧɟ ɨɝɪɚɧɢɱɟɧɵ (ɜ ɨɬɥɢɱɢɟ
ɨɬ ɩɪɢɧɰɢɩɚ ɉɚɭɥɢ ɜ ɮɟɪɦɢɨɧɚɯ) ɢ ɦɨɝɭɬ ɢɦɟɬɶ ɩɪɨɢɡɜɨɥɶɧɵɟ
ɡɧɚɱɟɧɢɹ. Ɏɭɧɤɰɢɸ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɛɨɡɟ-ɱɚɫɬɢɰ ɧɟɫɥɨɠɧɨ ɩɨ-
ɥɭɱɢɬɶ, ɪɚɫɫɦɨɬɪɟɜ ɬɟɪɦɨɞɢɧɚɦɢɱɟɫɤɢɣ ɩɨɬɟɧɰɢɚɥ ɫɢɫɬɟɦɵ
, ɝɞɟ ɫɬɚɬɢɫɬɢɱɟɫɤɚɹ ɫɭɦɦɚ Q ɜ ɛɨɥɶɲɨɦ ɤɚɧɨɧɢ-
ɱɟɫɤɨɦ ɚɧɫɚɦɛɥɟ (ɫ ɭɱɟɬɨɦ ɯɢɦɢɱɟɫɤɨɝɨ ɩɨɬɟɧɰɢɚɥɚ
P
) ɢɞɥɹ
ɫɢɫɬɟɦɵ ɧɟɜɡɚɢɦɨɞɟɣɫɬɜɭɸɳɢɯ ɱɚɫɬɢɰ ɢɦɟɟɬ ɜɢɞ:
: TQln
QNTET
N
nN
n
k
n
n
k
k
¦¦ ¦
exp{ / }[ exp{ / }] (exp[ ( )])
PE
PH
, (9.3)
ɬɚɤ ɤɚɤ ɷɧɟɪɝɢɹ n
k
ɱɚɫɬɢɰ ɜ ɫɨɫɬɨɹɧɢɢ k ɪɚɜɧɚ
H
k
n
k
. Ɉɬɦɟɬɢɦ,
ɱɬɨ ɦɵ ɢɧɬɟɪɟɫɭɟɦɫɹ ɤɨɧɤɪɟɬɧɵɦ ɫɨɫɬɨɹɧɢɟɦ k ɢ ɟɝɨ ɡɚɩɨɥɧɟ-
ɧɢɟɦ, ɬɚɤ ɤɚɤ ɜ ɨɬɫɭɬɫɬɜɢɢ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ ɜɫɟ ɫɨɫɬɨɹɧɢɹ ɫɬɚ-
ɬɢɫɬɢɱɟɫɤɢ ɧɟɡɚɜɢɫɢɦɵ. Ɂɚɦɟɬɢɦ, ɱɬɨ ɦɵ ɩɨɥɭɱɢɥɢ ɜ (9.3)
ɝɟɨɦɟɬɪɢɱɟɫɤɭɸ ɩɪɨɝɪɟɫɫɢɸ, ɢ ɞɥɹ ɟɟ ɫɯɨɞɢɦɨɫɬɢ ɧɟɨɛɯɨɞɢ-
ɦɨ, ɱɬɨɛɵ
exp[ ( )]
E
P
H
k
1. ɗɬɨ ɭɫɥɨɜɢɟ ɞɨɥɠɧɨ ɜɵɩɨɥɧɹɬɶ-
160
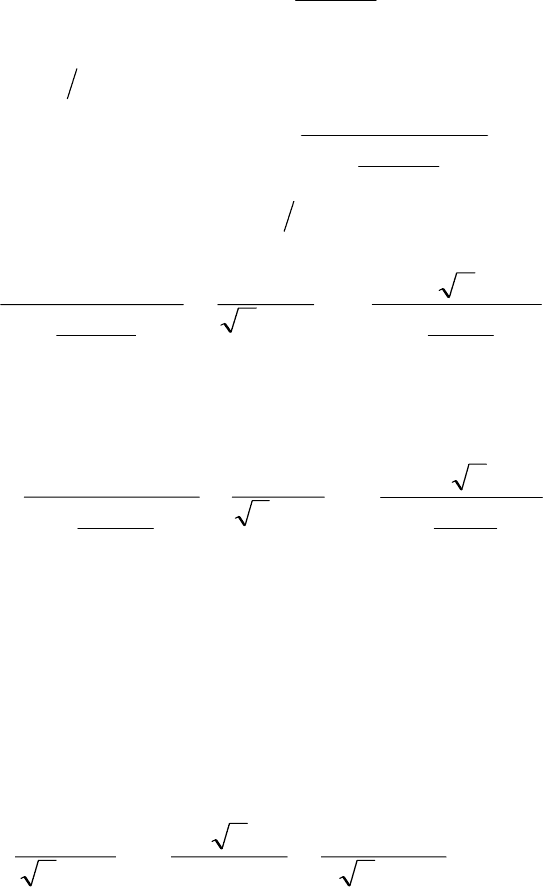
ɫɹ ɞɥɹ ɜɫɟɯ ɫɨɫɬɨɹɧɢɣ
H
k
, ɜ ɬɨɦ ɱɢɫɥɟ ɢ ɞɥɹ
H
k
=0. Ɉɬɫɸɞɚ ɯɢɦ-
ɩɨɬɟɧɰɢɚɥ ɞɨɥɠɟɧ ɛɵɬɶ ɨɬɪɢɰɚɬɟɥɟɧ:
P
<0. ɋɭɦɦɢɪɭɟɦ ɝɟɨ-
ɦɟɬɪɢɱɟɫɤɭɸ ɩɪɨɝɪɟɫɫɢɸ ɢ ɧɚɯɨɞɢɦ:
:
k
q
T
T
ln( exp[ ])1
P
H
. (9.4)
Ɍɟɩɟɪɶ ɦɨɠɧɨ ɧɚɣɬɢ ɫɪɟɞɧɢɟ ɱɢɫɥɚ ɡɚɩɨɥɧɟɧɢɹ
! n
kk
ww
:
P
:
nT n aa
T
kkkk
k
()
exp[ ]
! !
1
1
HP
. (9.5)
ɗɧɟɪɝɢɹ ɨɞɧɨɣ ɱɚɫɬɢɰɵ
H
k
km
!
22
2.ɉɨɥɧɨɟ ɱɢɫɥɨ ɱɚɫɬɢɰ
N
ɜ ɝɚɡɟ ɩɨɥɭɱɚɟɦ, ɫɭɦɦɢɪɭɹ (9.5):
N
T
Vm
d
T
k
k
¦
³
f
1
1
2
1
32
23
0
exp[ ] exp[ ]
/
HP
S
H
H
HP
!
. (9.6)
ɍɪɚɜɧɟɧɢɟ ɧɨɪɦɢɪɨɜɤɢ (9.6) ɨɩɪɟɞɟɥɹɟɬ ɧɟɹɜɧɨ ɯɢɦɢɱɟɫɤɢɣ
ɩɨɬɟɧɰɢɚɥ
P
ɤɚɤ ɮɭɧɤɰɢɸ ɬɟɦɩɟɪɚɬɭɪɵ
T
ɢ ɩɥɨɬɧɨɫɬɢ
n = N/V
.
ɗɧɟɪɝɢɹ ɛɨɡɟ-ɝɚɡɚ
E
T
Vm
d
T
k
k
k
¦
³
f
H
HP
S
H
HH
HP
1
1
2
1
32
23
0
exp[ ] exp[ ]
/
!
. (9.7)
Ɋɚɫɫɦɨɬɪɢɦ ɫɥɭɱɚɣ ɧɢɡɤɢɯ ɬɟɦɩɟɪɚɬɭɪ. ɉɪɢ ɧɢɡɤɢɯ
ɬɟɦɩɟɪɚɬɭɪɚɯ ɫɜɨɣɫɬɜɚ ɛɨɡɟ-ɝɚɡɚ ɤɚɪɞɢɧɚɥɶɧɨ ɨɬɥɢɱɚɸɬɫɹ ɨɬ
ɫɜɨɣɫɬɜ ɮɟɪɦɢ-ɝɚɡɚ ɯɨɬɹ ɛɵ ɩɨɬɨɦɭ, ɱɬɨ ɨɫɧɨɜɧɨɟ ɫɨɫɬɨɹɧɢɟ
ɫɢɫɬɟɦɵ ɢɦɟɟɬ ɷɧɟɪɝɢɸ
E=0 (ɬ.ɟ. ɜɫɟ ɱɚɫɬɢɰɵ ɫɤɨɧɞɟɧɫɢɪɨɜɚ-
ɧɵ ɜ ɫɨɫɬɨɹɧɢɟ ɫ
H
k
=0). ɋɨɝɥɚɫɧɨ ɧɨɪɦɢɪɨɜɨɱɧɨɦɭ ɭɪɚɜɧɟɧɢɸ
(9.6) ɩɪɢ ɩɨɧɢɠɟɧɢɢ ɬɟɦɩɟɪɚɬɭɪɵ ɯɢɦɢɱɟɫɤɢɣ ɩɨɬɟɧɰɢɚɥ
P
ɜɨɡɪɚɫɬɚɟɬ, ɛɭɞɭɱɢ ɨɬɪɢɰɚɬɟɥɶɧɵɦ, ɢ ɞɨɫɬɢɝɚɟɬ ɡɧɚɱɟɧɢɹ
P
=0
ɩɪɢ ɬɟɦɩɟɪɚɬɭɪɟ
T
0
, ɭɞɨɜɥɟɬɜɨɪɹɸɳɟɣ ɫɨɨɬɧɨɲɟɧɢɸ:
NV
mT
dz
z
z
mT
/
()
exp[ ]
()
(/)
//
/
f
³
0
32
23
0
0
32
32 3
2
1
22
32
SS
9
!!
. (9.8)
161

Ɂɞɟɫɶ ɭɱɬɟɧɨ, ɱɬɨ
xdx
z
ZZ
Z
f
³
1
0
1exp[ ]
()(),*
9
9
(Z) - ɞɡɟɬɚ-
ɮɭɧɤɰɢɹ Ɋɢɦɚɧɚ (
9
(3/2)=2.612), Ƚ(Z) - ɝɚɦɦɚ-ɮɭɧɤɰɢɹ
(Ƚ(3/2
)=1/2Ƚ(1/2)=
S
2). ɂɡ (9.8) ɩɨɥɭɱɚɟɦ ɬɟɦɩɟɪɚɬɭɪɭ (ɤɚɤ
ɦɵ ɭɜɢɞɢɦ ɧɢɠɟ, ɬɟɦɩɟɪɚɬɭɪɭ ɤɨɧɞɟɧɫɚɰɢɢ)
>@
T
m
N
Vm
N
V
0
23
2
23
2
23
2
32
331
S
9
(/)
() . ()
/
//
!!
. (9.9)
Ɂɚɦɟɬɢɦ, ɱɬɨ ɩɪɢ ɛɨɥɟɟ ɧɢɡɤɢɯ ɬɟɦɩɟɪɚɬɭɪɚɯ
T<T
0
ɭɪɚɜɧɟɧɢɟ
ɧɨɪɦɢɪɨɜɤɢ (9.6) ɧɟ ɢɦɟɟɬ ɪɟɲɟɧɢɣ
P
<0, ɯɨɬɹ ɷɬɨ ɞɨɥɠɧɨ
ɛɵɬɶ ɞɥɹ ɛɨɡɟ-ɫɬɚɬɢɫɬɢɤɢ. ɗɬɨ ɫɜɹɡɚɧɨ ɫ ɬɟɦ, ɱɬɨ ɧɟɥɶɡɹ ɜ ɷɬɨɦ
ɫɥɭɱɚɟ ɩɟɪɟɯɨɞɢɬɶ ɮɨɪɦɚɥɶɧɨ ɨɬ ɫɭɦɦɢɪɨɜɚɧɢɹ ɤ ɢɧɬɟɝɪɢɪɨ-
ɜɚɧɢɸ ɜ (9.6). ɇɟɨɛɯɨɞɢɦɨ ɛɨɥɟɟ ɚɤɤɭɪɚɬɧɨ ɭɱɢɬɵɜɚɬɶ ɱɥɟɧ ɫ
H
k
=0, ɬɚɤ ɤɚɤ ɨɧ ɭɦɧɨɠɚɟɬɫɹ ɧɚ
H
ɢ ɜɵɩɚɞɚɟɬ ɢɡ ɫɭɦɦɵ. Ɉɞ-
ɧɚɤɨ ɢɦɟɧɧɨ ɨɧ ɜɚɠɟɧ ɩɪɢ ɧɢɡɤɢɯ ɬɟɦɩɟɪɚɬɭɪɚɯ, ɬɚɤ ɤɚɤ ɢɦɟɧ-
ɧɨ ɜ ɷɬɨ ɫɨɫɬɨɹɧɢɟ ɤɨɧɞɟɧɫɢɪɭɸɬɫɹ ɜɫɟ ɱɚɫɬɢɰɵ. Ɏɨɪɦɚɥɶɧɨ
ɢɡ (9.6) ɦɨɠɧɨ ɡɚɦɟɬɢɬɶ, ɱɬɨ ɩɪɢ ɩɟɪɟɯɨɞɟ ɤ ɩɪɟɞɟɥɭ
Po
0
ɷɬɨɬ ɱɥɟɧ ɪɚɫɯɨɞɢɬɫɹ. ɍɫɬɪɟɦɥɹɹ
P
ɧɟ ɤ ɧɭɥɸ, ɚ ɤ ɧɟɤɨɬɨɪɨɦɭ
ɤɨɧɟɱɧɨɦɭ ɦɚɥɨɦɭ ɡɧɚɱɟɧɢɸ, ɦɨɠɧɨ ɟɝɨ ɩɪɢɜɟɫɬɢ ɤ ɤɨɧɟɱɧɨɣ
ɜɟɥɢɱɢɧɟ. Ɉɞɧɚɤɨ ɦɨɠɧɨ ɮɨɪɦɚɥɶɧɨ ɨɛɨɣɬɢ ɷɬɨɬ ɦɨɦɟɧɬ, ɪɚɫ-
ɫɱɢɬɚɜ ɫɧɚɱɚɥɚ ɱɢɫɥɨ ɱɚɫɬɢɰ ɩɪɢ
H
>0 (ɩɪɢ T<T
0
), ɬɚɤ ɤɚɤ ɷɬɚ
ɜɟɥɢɱɢɧɚ, ɨɩɪɟɞɟɥɹɟɦɚɹ (9.6) ɫ
P
=0, ɤɨɧɟɱɧɚ:
N
VmT
dz
z
z
N
T
T
H
S
!
f
³
0
32
23
0
0
32
2
1
()
exp[ ]
{}
/
/
!
(9.10)
(ɡɞɟɫɶ ɦɵ ɢɫɩɨɥɶɡɨɜɚɥɢ ɨɩɪɟɞɟɥɟɧɢɟ
T
0
(9.8)). Ɉɫɬɚɥɶɧɵɟ
ɫɤɨɧɞɟɧɫɢɪɨɜɚɧɧɵɟ ɩɪɢ
H
=0
ɱɚɫɬɢɰɵ ɨɩɪɟɞɟɥɹɸɬɫɹ ɢɡ ɧɨɪɦɢ-
ɪɨɜɤɢ
NNNTT
H
00 0
32
1[( )
/
]
. (9.11)
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɩɪɢ ɬɟɦɩɟɪɚɬɭɪɟ T=T
0
ɧɚɱɢɧɚɟɬɫɹ ɤɨɧ-
ɞɟɧɫɚɰɢɹ ɛɨɡɟ-ɱɚɫɬɢɰ ɜ ɧɚɢɧɢɡɲɟɟ ɷɧɟɪɝɟɬɢɱɟɫɤɨɟ ɫɨɫɬɨɹɧɢɟ
162

H
=0, ɢ ɱɢɫɥɨ ɫɤɨɧɞɟɧɫɢɪɨɜɚɧɧɵɯ ɱɚɫɬɢɰ N
0
ɨɩɪɟɞɟɥɹɟɬɫɹ ɫɬɟ-
ɩɟɧɧɨɣ ɡɚɜɢɫɢɦɨɫɬɶɸ (9.11).
Ɉɩɪɟɞɟɥɢɦ ɬɟɪɦɨɞɢɧɚɦɢɱɟɫɤɢɟ ɜɟɥɢɱɢɧɵ ɛɨɡɟ-ɝɚɡɚ ɜ
ɭɫɥɨɜɢɹɯ ɧɚɥɢɱɢɹ ɤɨɧɞɟɧɫɚɬɚ (T<T
0
). ȿɫɬɟɫɬɜɟɧɧɨ, ɨɧɢ ɨɩɪɟ-
ɞɟɥɹɸɬɫɹ ɬɨɥɶɤɨ ɱɚɫɬɢɰɚɦɢ ɫ
H
>0 . ɉɨɥɚɝɚɹ ɜɟɡɞɟ
P
=0, ɧɚɯɨ-
ɞɢɦ ɷɧɟɪɝɢɸ E, ɬɟɩɥɨɟɦɤɨɫɬɶ C, ɷɧɬɪɨɩɢɸ S ɢ ɫɜɨɛɨɞɧɭɸ
ɷɧɟɪɝɢɸ F:
E
Vm
T
VmT T
NT T T
CETETT
SCTTET
FETS E
f
³
³
32
23
0
32
32 3
0
32
32
2
1
3
42
52
0770
52
53
2
3
//
/
/
/
exp[ ]
()
(/)
.[],
~,
[] ,
.
S
H
HH
H
S
9
ww
!!
d
d
(9.12)
ȼ ɬɨɱɤɟ T=T
0
ɜɫɟ ɜɟɥɢɱɢɧɵ (9.12) ɧɟɩɪɟɪɵɜɧɵ. Ɉɞɧɚɤɨ ɩɪɨɢɡ-
ɜɨɞɧɚɹ ɬɟɩɥɨɟɦɤɨɫɬɢ ɢɫɩɵɬɵɜɚɟɬ ɜ ɷɬɨɣ ɬɨɱɤɟ ɤɨɧɟɱɧɵɣ ɫɤɚ-
ɱɨɤ (ɫɦ. ɧɢɠɟ ɡɚɞɚɱɭ), ɬ.ɟ. ɬɟɩɥɨɟɦɤɨɫɬɶ ɢɦɟɟɬ ɩɪɢ T=T
0
ɢɡ-
ɥɨɦ ɢ ɪɚɜɧɚ 1.92N. Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɹɜɥɟɧɢɟ ɛɨɡɟ-ɤɨɧɞɟɧɫɚɰɢɢ -
ɬɢɩɢɱɧɵɣ ɮɚɡɨɜɵɣ ɩɟɪɟɯɨɞ ɜɬɨɪɨɝɨ ɪɨɞɚ.
Ɂɚɞɚɱɢ
9.1.
1. Ɋɚɫɫɱɢɬɚɬɶ ɫɤɚɱɨɤ ɩɪɨɢɡɜɨɞɧɨɣ ɬɟɩɥɨɟɦɤɨɫɬɢ
dC/dT ɜ ɬɨɱɤɟ T=T
0
ɞɥɹ ɛɨɡɟ-ɝɚɡɚ, ɬ.ɟ. ɡɧɚɱɟɧɢɟ dC/dT ɩɪɢ T=T
0
- 0 ɢ T=T
0
+ 0.
ɍɤɚɡɚɧɢɟ
: ɩɪɢ T=T
0
+0 ɫɥɟɞɭɟɬ ɪɚɡɥɨɠɢɬɶ ɷɧɟɪɝɢɸ ɩɪɢ
ɦɚɥɵɯ T-T
0
, ɚ ɬɚɤɠɟ ɧɚɣɬɢ ɡɚɜɢɫɢɦɨɫɬɶ ɨɬ ɬɟɦɩɟɪɚɬɭɪɵ ɯɢɦɢ-
ɱɟɫɤɨɝɨ ɩɨɬɟɧɰɢɚɥɚ ɩɪɢ T-T
0
<<T
0
, ɩɨɥɚɝɚɹ ɟɝɨ ɦɚɥɵɦ ɨɬɪɢ-
ɰɚɬɟɥɶɧɵɦ ɱɢɫɥɨɦ -
P
~ (T-T
0
)
D
<<T
0
.
163

9.2. ȼɨɡɛɭɠɞɟɧɢɹ ɜ ɫɥɚɛɨ ɧɟɢɞɟɚɥɶɧɨɦ ɛɨɡɟ-ɝɚɡɟ
Ɉɛɫɭɞɢɦ ɫɧɚɱɚɥɚ ɤɚɱɟɫɬɜɟɧɧɨ ɜɨɡɦɨɠɧɵɟ ɜɨɡɛɭɠɞɟɧɢɹ
ɜ ɛɨɡɟ-ɝɚɡɟ ɜ ɞɥɢɧɧɨɜɨɥɧɨɜɨɦ ɩɪɟɞɟɥɟ p
o
0. ȼ ɤɜɚɧɬɨɜɨɣ ɛɨɡɟ-
ɫɢɫɬɟɦɟ ɷɥɟɦɟɧɬɚɪɧɵɟ ɜɨɡɛɭɠɞɟɧɢɹ ɞɨɥɠɧɵ ɢɦɟɬɶ ɰɟɥɨɱɢɫ-
ɥɟɧɧɵɣ ɫɩɢɧ, ɬɚɤ ɤɚɤ ɦɨɦɟɧɬ ɢɦɩɭɥɶɫɚ ɜɫɹɤɨɣ ɤɜɚɧɬɨɜɨ-
ɦɟɯɚɧɢɱɟɫɤɨɣ ɫɢɫɬɟɦɵ ɦɨɠɟɬ ɦɟɧɹɬɶɫɹ ɬɨɥɶɤɨ ɧɚ ɰɟɥɨɟ ɱɢɫɥɨ.
ɉɨɷɬɨɦɭ ɜ ɤɜɚɧɬɨɜɨɣ ɛɨɡɟ-ɠɢɞɤɨɫɬɢ ɷɥɟɦɟɧɬɚɪɧɵɦɢ ɜɨɡɛɭɠ-
ɞɟɧɢɹɦɢ ɫ ɦɚɥɵɦɢ ɢɦɩɭɥɶɫɚɦɢ p ɹɜɥɹɸɬɫɹ ɨɛɵɱɧɵɟ ɝɢɞɪɨɞɢ-
ɧɚɦɢɱɟɫɤɢɟ ɜɨɥɧɵ, ɬ.ɟ. ɮɨɧɨɧɵ (ɤɜɚɡɢɱɚɫɬɢɰɵ ɫ ɧɭɥɟɜɵɦ ɫɩɢ-
ɧɨɦ
). Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɡɚɤɨɧ ɞɢɫɩɟɪɫɢɢ ɜɨɡɛɭɠɞɟɧɢɣ ɞɨɥɠɟɧ
ɛɵɬɶ ɥɢɧɟɟɧ:
H
p
= u p , (9.13)
ɝɞɟ ɪɚɡɦɟɪɧɵɣ ɤɨɷɮɮɢɰɢɟɧɬ u ɢɦɟɟɬ ɫɦɵɫɥ ɫɤɨɪɨɫɬɢ ɡɜɭɤɚ.
ɑɢɫɥɨ ɷɬɢɯ ɜɨɡɛɭɠɞɟɧɢɣ ɫɬɪɟɦɢɬɫɹ ɤ ɧɭɥɸ ɩɪɢ T
o
0, ɢ ɩɪɢ
ɧɢɡɤɢɯ ɬɟɦɩɟɪɚɬɭɪɚɯ, ɤɨɝɞɚ ɢɯ ɱɢɫɥɨ ɦɚɥɨ, ɢ ɨɧɢ ɩɪɚɤɬɢɱɟɫɤɢ
ɧɟ ɜɡɚɢɦɨɞɟɣɫɬɜɭɸɬ, ɢɯ ɦɨɠɧɨ ɫɱɢɬɚɬɶ ɢɞɟɚɥɶɧɵɦ ɛɨɡɟ-ɝɚɡɨɦ
ɫ ɧɭɥɟɜɵɦ ɯɢɦɩɨɬɟɧɰɢɚɥɨɦ
P
=0 (ɱɢɫɥɨ ɜɨɡɛɭɠɞɟɧɢɣ ɧɟ ɮɢɤ-
ɫɢɪɨɜɚɧɨ), ɢ ɮɭɧɤɰɢɹ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɜɨɡɛɭɠɞɟɧɢɣ
np
T
p
()
exp[ ]
.
1
1
H
(9.14)
Ɇɨɠɧɨ, ɡɧɚɹ ɪɚɫɩɪɟɞɟɥɟɧɢɟ (9.14) ɢ ɡɚɤɨɧ ɞɢɫɩɟɪɫɢɢ
(9.13), ɪɚɫɫɱɢɬɚɬɶ ɬɟɪɦɨɞɢɧɚɦɢɱɟɫɤɢɟ ɜɟɥɢɱɢɧɵ ɠɢɞɤɨɫɬɢ ɩɪɢ
ɧɢɡɤɢɯ ɬɟɦɩɟɪɚɬɭɪɚɯ, ɚɧɚɥɨɝɢɱɧɨ ɬɨɦɭ, ɤɚɤ ɦɵ ɪɚɫɫɱɢɬɚɥɢ
ɬɟɪɦɨɞɢɧɚɦɢɤɭ ɢɞɟɚɥɶɧɨɝɨ ɛɨɡɟ-ɝɚɡɚ:
EV dp
up
up T u
VT
f
³
1
21
3
3
0
2
3
4
() exp[ ]
,
S
S
30
(9.15)
164

ɝɞɟ
CET ETT
SCTdTET
FETS E
³
ww
4
43
1
3
3
~,
[]
.
,
ɉɪɢ ɭɜɟɥɢɱɟɧɢɢ ɢɦɩɭɥɶɫɚ ɡɚɤɨɧ ɞɢɫɩɟɪɫɢɢ ɨɬɥɢɱɚɟɬɫɹ ɨɬ ɥɢ-
ɧɟɣɧɨɝɨ (9.13), ɢ ɞɚɥɶɧɟɣɲɢɣ ɯɨɞ ɡɚɜɢɫɢɦɨɫɬɢ ɨɩɪɟɞɟɥɹɟɬɫɹ
ɜɡɚɢɦɨɞɟɣɫɬɜɢɟɦ ɦɟɠɞɭ ɱɚɫɬɢɰɚɦɢ ɛɨɡɟ-ɝɚɡɚ.
ɉɨɥɭɱɢɦ ɛɨɥɟɟ ɤɨɪɪɟɤɬɧɨ ɡɚɤɨɧ ɜɨɡɛɭɠɞɟɧɢɣ ɧɚɞ ɨɫ-
ɧɨɜɧɵɦ ɫɨɫɬɨɹɧɢɟɦ ɜɡɚɢɦɨɞɟɣɫɬɜɭɸɳɟɝɨ ɛɨɡɟ-ɝɚɡɚ. Ɋɚɫɫɦɨɬ-
ɪɢɦ ɫɥɚɛɨ ɧɟɢɞɟɚɥɶɧɵɣ ɛɨɡɟ-ɝɚɡ ɫ ɨɞɢɧɚɤɨɜɵɦ ɜɡɚɢɦɨɞɟɣɫɬɜɢ-
ɟɦ U ɦɟɠɞɭ ɩɚɪɚɦɢ ɱɚɫɬɢɰ, ɨɩɢɫɵɜɚɟɦɵɣ ɝɚɦɢɥɶɬɨɧɢɚɧɨɦ:
Haa
U
V
aaaa
ppp p p p p
pp pp
pp pp
p
¦¦
H
2
4321
1234
1234
, (9.16)
ɝɞɟ
H
p
=p
2
/2m , ɚ ɜɡɚɢɦɨɞɟɣɫɬɜɢɟ U ɫɜɹɡɚɧɨ ɫ ɚɦɩɥɢɬɭɞɨɣ ɪɚɫ-
ɫɟɹɧɢɹ a (ɢɦɟɸɳɟɣ ɜɟɥɢɱɢɧɭ ɩɨɪɹɞɤɚ ɦɟɠɱɚɫɬɢɱɧɨɝɨ ɪɚɫɫɬɨɹ-
ɧɢɹ [a
3
~ V/N] ) ɦɟɠɞɭ ɞɜɭɦɹ ɨɞɢɧɚɤɨɜɵɦɢ ɱɚɫɬɢɰɚɦɢ ɫɨɨɬ-
ɧɨɲɟɧɢɟɦ
U=4
S
a/m. (9.16a)
Ȼɨɝɨɥɸɛɨɜ (1947 ɝ.) ɩɨɤɚɡɚɥ, ɱɬɨ ɞɥɹ ɨɩɢɫɚɧɢɹ ɨɫɧɨɜɧɨ-
ɝɨ ɢ ɧɢɡɲɢɯ ɜɨɡɛɭɠɞɟɧɧɵɯ ɫɨɫɬɨɹɧɢɣ ɭɞɚɟɬɫɹ ɞɢɚɝɨɧɚɥɢɡɨ-
ɜɚɬɶ ɝɚɦɢɥɶɬɨɧɢɚɧ (9.16) ɢ ɩɨɥɭɱɢɬɶ ɷɧɟɪɝɟɬɢɱɟɫɤɢɣ ɫɩɟɤɬɪ.
ɍɩɪɨɫɬɢɦ ɜɡɚɢɦɨɞɟɣɫɬɜɭɸɳɭɸ ɱɚɫɬɶ ɝɚɦɢɥɶɬɨɧɢɚɧɚ, ɭɱɢɬɵ-
ɜɚɹ, ɱɬɨ ɜ ɨɫɧɨɜɧɨɦ ɫɨɫɬɨɹɧɢɢ ɱɚɫɬɢɰɵ ɧɚɯɨɞɹɬɫɹ ɜ ɤɨɧɞɟɧɫɚ-
ɬɟ, ɢ ɜɜɢɞɭ ɫɥɚɛɨɫɬɢ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ ɨɫɧɨɜɧɨɟ ɫɨɫɬɨɹɧɢɟ
ɜɡɚɢɦɨɞɟɣɫɬɜɭɸɳɟɝɨ ɝɚɡɚ ɛɭɞɟɬ ɫɥɚɛɨ ɨɬɥɢɱɚɬɶɫɹ ɨɬ ɨɫɧɨɜɧɨ-
ɝɨ
ɫɨɫɬɨɹɧɢɹ ɢɞɟɚɥɶɧɨɝɨ ɝɚɡɚ, ɩɨɷɬɨɦɭ ɱɢɫɥɨ ɱɚɫɬɢɰ ɧɚɞ ɤɨɧ-
ɞɟɧɫɚɬɨɦ ɛɭɞɟɬ ɦɧɨɝɨ ɦɟɧɶɲɟ ɱɢɫɥɚ ɤɨɧɞɟɧɫɚɬɧɵɯ ɱɚɫɬɢɰ N
0
:
165
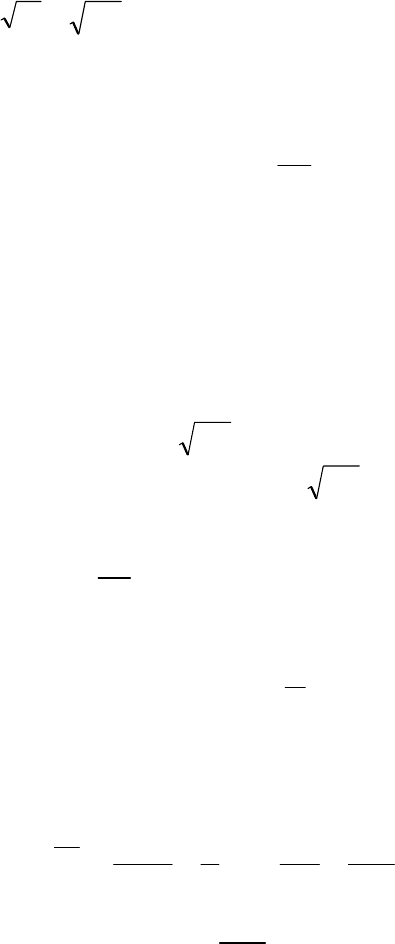
N - N
0
<< N
0
.
Ɍɚɤ ɤɚɤ ɦɚɬɪɢɱɧɵɟ ɷɥɟɦɟɧɬɵ ɛɨɡɟɜɫɤɢɯ ɨɩɟɪɚɬɨɪɨɜ ɪɚɜɧɵ
NN~
0
>> 1 (ɫɦ. (9.2)), ɬɨ ɜ (9.16) ɦɨɠɧɨ ɨɫɬɚɜɢɬɶ ɬɨɥɶɤɨ
ɜɡɚɢɦɨɞɟɣɫɬɜɢɟ ɤɨɧɞɟɧɫɚɬɧɵɯ ɱɚɫɬɢɰ ɦɟɠɞɭ ɫɨɛɨɣ ɢ ɫ ɜɨɡɛɭ-
ɠɞɟɧɢɹɦɢ, ɩɪɟɧɟɛɪɟɝɚɹ ɜɡɚɢɦɨɞɟɣɫɬɜɢɟɦ ɧɚɞɤɨɧɞɟɧɫɚɬɧɵɯ
ɱɚɫɬɢɰ ɦɟɠɞɭ ɫɨɛɨɣ:
H
U
V
aaaa
aaaa aaaa aaaa aaaa
pp p p pp pp
p
int
{
()
z
¦
2
22
0000
00 0 0 0000
0
}.
(9.17)
ȼ (9.17) ɭɱɬɟɧɵ ɩɪɨɰɟɫɫɵ ɪɨɠɞɟɧɢɹ (ɭɧɢɱɬɨɠɟɧɢɹ) ɩɚɪɵ ɜɨɡ-
ɛɭɠɞɟɧɢɣ ɢɡ ɤɨɧɞɟɧɫɚɬɚ (ɜ ɤɨɧɞɟɧɫɚɬ) - ɩɨɫɥɟɞɧɢɟ ɞɜɚ ɱɥɟɧɚ (ɫ
ɫɨɯɪɚɧɟɧɢɟɦ ɫɭɦɦɚɪɧɨɝɨ ɢɦɩɭɥɶɫɚ p+(-p)=0), ɚ ɬɚɤɠɟ ɨɞɧɨ-
ɱɚɫɬɢɱɧɨɟ ɪɚɫɫɟɹɧɢɟ ɜɨɡɛɭɠɞɟɧɢɰ ɧɚ ɤɨɧɞɟɧɫɚɬɧɨɣ ɱɚɫɬɢɰɟ
(ɩɟɪɜɵɟ ɞɜɚ ɱɥɟɧɚ).
Ɍɚɤ ɤɚɤ
N
0
>> 1, ɨɩɟɪɚɬɨɪɵ a
+
0
ɢ a
0
ɹɜɥɹɸɬɫɹ ɩɪɨ-
ɫɬɵɦɢ ɱɢɫɥɚɦɢ, ɪɚɜɧɵɦɢ
N
0
. Ɉɬɫɸɞɚ ɜɡɚɢɦɨɞɟɣɫɬɜɭɸɳɚɹ
ɱɚɫɬɶ ɝɚɦɢɥɶɬɨɧɢɚɧɚ ɩɟɪɟɩɢɫɵɜɚɟɬɫɹ ɜ ɜɢɞɟ
H
U
V
NN aa aa aa aa
pp pp pp pp
p
int
()
ª
¬
«
º
¼
»
z
¦
2
22
0
2
0
0
. (9.18)
ɍɱɬɟɦ ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɩɨɥɧɨɝɨ ɱɢɫɥɚ ɱɚɫɬɢɰ:
NN aa aa
pp p p
p
z
¦
0
0
1
2
()
. (9.19)
ȼɵɪɚɡɢɦ ɜɫɟ ɱɢɫɥɚ N
0
ɱɟɪɟɡ N ɜ (9.18), ɨɝɪɚɧɢɱɢɜɚɹɫɶ ɱɥɟɧɚ-
ɦɢ, ɫɨɞɟɪɠɚɳɢɦɢ ɧɟ ɦɟɧɟɟ ɩɟɪɜɨɣ ɫɬɟɩɟɧɢ N. ɋ ɭɱɟɬɨɦ (9.19)
ɢ (9.18) ɩɨɥɧɵɣ ɝɚɦɢɥɶɬɨɧɢɚɧ (9.16) ɩɟɪɟɩɢɫɵɜɚɟɬɫɹ ɜ ɜɢɞɟ:
H
UN
V
p
m
UN
V
aa a a
UN
V
aa aa
pp p p
p
pp pp
z
¦
22
0
2
1
22
[( )( )
()].
(9.20)
166
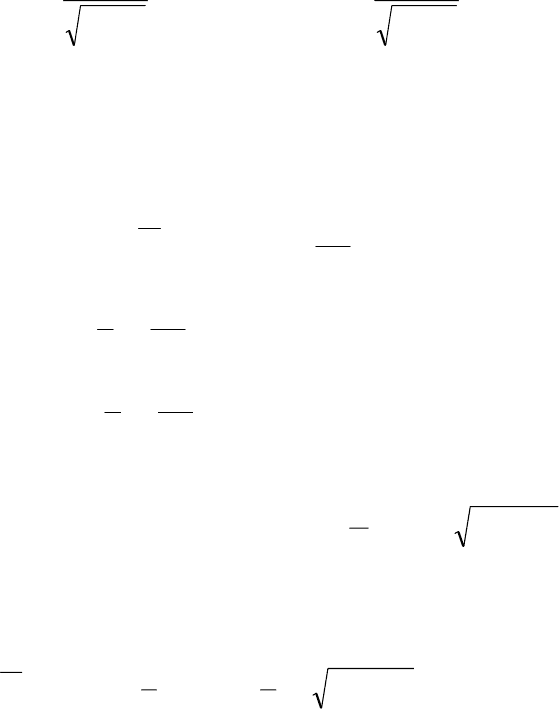
Ⱦɢɚɝɨɧɚɥɢɡɭɟɦ ɝɚɦɢɥɶɬɨɧɢɚɧ (9.20). Ⱦɥɹ ɷɬɨɝɨ ɜɜɟɞɟɦ ɥɢɧɟɣ-
ɧɵɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɨɩɟɪɚɬɨɪɨɜ:
a
A
Aa
A
A
p
p
ppp p
p
ppp
1
1
1
1
22
(), (
DD DD
). (9.21)
ɇɟɫɥɨɠɧɨ ɭɛɟɞɢɬɶɫɹ, ɱɬɨ ɨɩɟɪɚɬɨɪɵ
D
ɬɚɤɠɟ ɭɞɨɜɥɟɬɜɨɪɹɸɬ
ɛɨɡɟɜɫɤɢɦ ɫɨɨɬɧɨɲɟɧɢɹɦ ɤɨɦɦɭɬɚɰɢɢ. ɉɨɞɫɬɚɜɢɜ ɢɯ ɜ ɝɚɦɢɥɶ-
ɬɨɧɢɚɧ (9.20) ɢ ɨɛɨɡɧɚɱɢɜ
S=UN/V, S
p
=p
2
/2m+S,
'
p
=1+A
p
2
, W
p
=1-A
p
2
, (9.22)
ɩɨɥɭɱɢɦ
>@
>@
>@
HSN
W
SA SA
W
SSA
W
SA S
p
pp p
p
p
pp p pp p p
p
p
pp p p p p p
p
z
z
z
¦
¦
¦
/
{}(
{}(
2
1
1
2
1
2
1
2
1
2
2
0
0
0
'
'
DD D D
DD DD
)
).
(9.23)
Ɂɚɧɭɥɹɹ ɤɨɷɮɮɢɰɢɟɧɬ ɩɪɢ ɧɟɞɢɚɝɨɧɚɥɶɧɨɦ ɱɥɟɧɟ, ɧɚɯɨɞɢɦ A
p
:
20
1
22
SA S A
S
SSS
pp p p p p
' ( ). (9.24)
ȼ (9.24) ɩɟɪɟɞ ɤɨɪɧɟɦ ɩɨɫɬɚɜɥɟɧ ɡɧɚɤ “+” ɢɡ-ɡɚ ɩɨɥɨɠɢɬɟɥɶɧɨ-
ɫɬɢ ɷɧɟɪɝɢɢ ɜɨɡɛɭɠɞɟɧɢɣ ɨɬɧɨɫɢɬɟɥɶɧɨ ɨɫɧɨɜɧɨɝɨ ɫɨɫɬɨɹɧɢɹ
H
=0. ɉɨɞɫɬɚɜɢɜ (9.24) ɜ (9.23), ɧɚɯɨɞɢɦ ɨɤɨɧɱɚɬɟɥɶɧɨ:
HSN SA S S
p
p
pppp
p
z
z
¦¦
/(2
1
2
1
2
0
22
0
DD D D
p
)
. (9.25)
ȼɢɞɧɨ, ɱɬɨ (9.25) ɫɨɫɬɨɢɬ ɢɡ ɧɟɤɨɬɨɪɨɣ ɤɨɧɫɬɚɧɬɵ E
0
, ɢɦɟɸ-
ɳɟɣ ɫɦɵɫɥ ɷɧɟɪɝɢɢ ɨɫɧɨɜɧɨɝɨ ɫɨɫɬɨɹɧɢɹ ɛɨɡɟ-ɠɢɞɤɨɫɬɢ, ɢ
ɷɧɟɪɝɢɢ ɜɨɡɛɭɠɞɟɧɢɣ ɫɨ ɫɩɟɤɬɪɨɦ E
p
, ɬɚɤ ɱɬɨ ɩɨɥɧɚɹ ɷɧɟɪɝɢɹ
ɫɢɫɬɟɦɵ ɢɦɟɟɬ ɜɢɞ
167
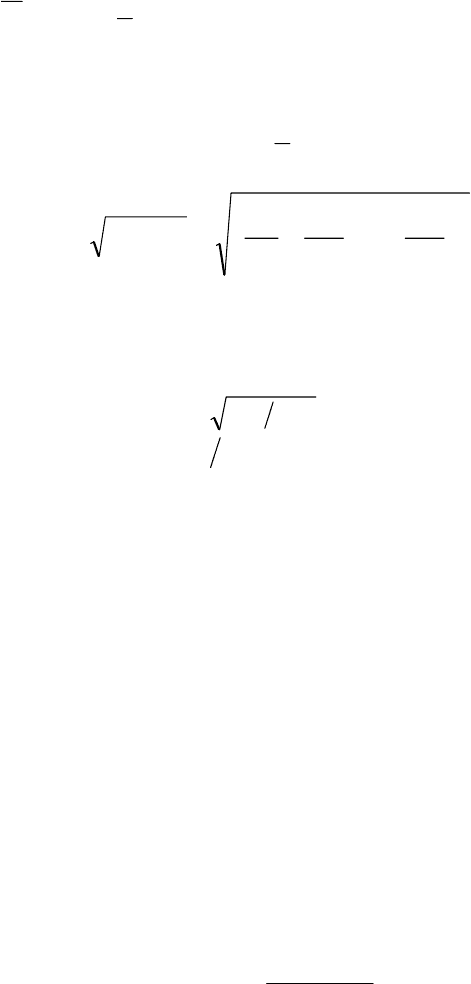
EHE E E En
n
ESN SA
ESS
p
m
UN
V
UN
V
ppp pp
p
pp
p
pp p
p
p
pp
! !
!
§
©
¨
·
¹
¸
§
©
¨
·
¹
¸
zz
z
¦¦
¦
0
0
0
0
0
0
22
2
2
2
1
2
2
1
2
2
DD D D
DD
,
,
/,
.
(9.26)
Ɂɞɟɫɶ n
p
- ɮɭɧɤɰɢɹ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɜɨɡɛɭɠɞɟɧɢɣ (9.14), ɢɦɟɸ-
ɳɚɹ ɜɢɞ ɛɨɡɟ-ɮɭɧɤɰɢɢ ɫ ɧɭɥɟɜɵɦ ɯɢɦɩɨɬɟɧɰɢɚɥɨɦ. ȼɩɪɟ-
ɞɟɥɶɧɵɯ ɫɥɭɱɚɹɯ ɫɩɟɤɬɪ ɜɨɡɛɭɠɞɟɧɢɣ ɢɦɟɟɬ ɜɢɞ:
E
up u UN mV p
pm p
p
of
®
°
¯
°
,,
,.
0
2
2
o
;
(9.27)
ɉɪɢ ɦɚɥɵɯ ɢɦɩɭɥɶɫɚɯ ɦɵ ɩɨɥɭɱɚɟɦ, ɤɚɤ ɢ ɫɥɟɞɨɜɚɥɨ ɨɠɢɞɚɬɶ,
ɡɜɭɤɨɜɨɣ ɡɚɤɨɧ ɞɢɫɩɟɪɫɢɢ ɫɨ ɫɤɨɪɨɫɬɶɸ ɡɜɭɤɚ u. ɉɪɢ ɛɨɥɶɲɢɯ
ɢɦɩɭɥɶɫɚɯ ɢɦɟɟɦ ɫɩɟɤɬɪ ɫɜɨɛɨɞɧɨɣ ɱɚɫɬɢɰɵ, ɬɚɤ ɤɚɤ ɜɡɚɢɦɨ-
ɞɟɣɫɬɜɢɟ ɩɟɪɟɫɬɚɟɬ ɢɝɪɚɬɶ ɫɭɳɟɫɬɜɟɧɧɭɸ ɪɨɥɶ.
ɂɡ ɜɢɞɚ ɫɩɟɤɬɪɚ ɜɨɡɛɭɠɞɟɧɢɣ ɜɢɞɧɨ, ɱɬɨ ɥɨɤɚɥɶɧɵɯ
ɦɢɧɢɦɭɦɨɜ ɧɚ ɧɟɦ ɧɟɬ, ɬɚɤ ɤɚɤ ɫɦɟɧɟ ɥɢɧɟɣɧɨɣ ɧɚ ɤɜɚɞɪɚɬɢɱ-
ɧɭɸ ɡɚɜɢɫɢɦɨɫɬɶ
ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɬɨɥɶɤɨ ɬɨɱɤɚ ɩɟɪɟɝɢɛɚ
(ɪɢɫ.18,ɚ). Ɉɞɧɚɤɨ ɦɵ ɪɚɫɫɦɚɬɪɢɜɚɥɢ ɫɥɚɛɨ ɧɟɢɞɟɚɥɶɧɵɣ ɝɚɡ. ȼ
ɪɟɚɥɶɧɨɦ ɠɟ ɫɥɭɱɚɟ ɩɪɢ ɜɨɡɪɚɫɬɚɧɢɢ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ ɜɨɡɦɨ-
ɠɟɧ ɥɨɤɚɥɶɧɵɣ ɦɢɧɢɦɭɦ (ɪɢɫ.18,ɛ) (ɱɬɨ ɧɚɛɥɸɞɚɟɬɫɹ ɭ ɠɢɞɤɨ-
ɝɨ ɝɟɥɢɹ). ȼɛɥɢɡɢ ɬɨɱɤɢ ɦɢɧɢɦɭɦɚ p
0
( ~ 1/a, a - ɦɟɠɚɬɨɦɧɨɟ
ɪɚɫɫɬɨɹɧɢɟ ), ɤɨɬɨɪɚɹ ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɧɨɜɵɦ ɤɜɚɡɢɱɚɫɬɢɱɧɵɦ
ɜɨɡɛɭɠɞɟɧɢɹɦ, ɦɨɠɧɨ ɪɚɡɥɨɠɢɬɶ ɪɟɚɥɶɧɵɣ ɫɩɟɤɬɪ E
p
ɜ ɜɢɞɟ
E
pp
m
p
'
(
*
0
2
2
)
, (9.28)
168
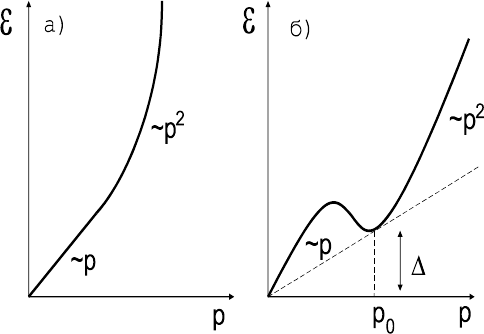
Ɋɢɫ
. 18.
ɋɩɟɤɬɪ ɜɨɡɛɭɠɞɟɧɢɣ ɜɡɚɢɦɨɞɟɣɫɬɜɭɸɳɟ
-
ɝɨ ɛɨɡɟ
-
ɝɚɡɚ
:
ɚ
) -
ɫɥɚɛɨɟ ɜɡɚɢɦɨɞɟɣɫɬɜɢɟ
;
ɛ
) -
ɫɢɥɶɧɨɟ ɜɡɚɢɦɨɞɟɣɫɬɜɢɟ
.
ɒɬɪɢɯɨɜɚɹ ɩɪɹɦɚɹ ɩɨ
-
ɤɚɡɵɜɚɟɬ
,
ɱɬɨ ɬɨɱɤɚ p
0
(
ɪɨɬɨɧɧɵɟ ɜɨɡɛɭɠɞɟɧɢɹ
)
ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɤɪɢɬɟɪɢɸ Ʌɚɧɞɚɭ
ddp p
H
H
//
,
ɬ
.
ɟ
.
ɫɜɟɪɯɬɟɤɭɱɟɫɬɶ ɢɦɟɟɬ ɦɟɫɬɨ
,
ɟɫɥɢ ɫɤɨɪɨɫɬɶ
ɞɜɢɠɟɧɢɹ ɠɢɞɤɨɫɬɢ v <
'
/p
0
ɝɞɟ
'
=E(p
0
), m* - ɷɮɮɟɤɬɢɜɧɚɹ ɦɚɫɫɚ ɷɬɢɯ ɜɨɡɛɭɠɞɟɧɢɣ, ɧɚɡɵ-
ɜɚɟɦɵɯ ɪɨɬɨɧɚɦɢ.
169
T
ɉɨɥɶɡɭɹɫɶ ɡɚɤɨɧɨɦ ɞɢɫɩɟɪɫɢɢ (9.28), ɩɨɥɭɱɢɦ ɜɤɥɚɞ ɜ
ɬɟɪɦɨɞɢɧɚɦɢɱɟɫɤɢɟ ɜɟɥɢɱɢɧɵ ɪɨɬɨɧɧɵɯ ɜɨɡɛɭɠɞɟɧɢɣ. ɉɪɢ
ɧɢɡɤɢɯ ɬɟɦɩɟɪɚɬɭɪɚɯ, ɩɨɥɚɝɚɹ
'
>>T (ɪɟɚɥɶɧɵɟ ɨɰɟɧɤɢ ɞɥɹ
ɠɢɞɤɨɝɨ ɝɟɥɢɹ
'
=8.7K), ɦɨɠɟɦ ɫɱɢɬɚɬɶ, ɱɬɨ ɪɚɫɩɪɟɞɟɥɟɧɢɟ
ɪɨɬɨɧɨɜ - ɛɨɥɶɰɦɚɧɨɜɫɤɨɟ:.Ɉɬɫɸɞɚ ɧɚɯɨ-
ɞɢɦ ɜ ɷɬɨɦ ɩɪɟɞɟɥɟ (ɭɱɢɬɵɜɚɹ ɬɚɤɠɟ, ɱɬɨ p
nE
pp
exp( / )
0
2
>>m*T ɢɩɪɢɢɧ-
ɬɟɝɪɢɪɨɜɚɧɢɢ ɭɞɨɛɧɨ ɩɟɪɟɣɬɢ ɤ ɩɟɪɟɦɟɧɧɨɣ x=p-p
0
, -
f<x<f):
