Елесин В.Ф., Кашурников В.А. Физика фазовых переходов
Подождите немного. Документ загружается.


8.3. Ɇɨɞɟɥɶ ɏɚɛɛɚɪɞɚ
Ⱦɥɹ ɨɛɴɹɫɧɟɧɢɹ ɮɚɡɨɜɵɯ ɩɟɪɟɯɨɞɨɜ ɦɟɬɚɥɥ-ɢɡɨɥɹɬɨɪ ɜ
ɩɟɪɟɯɨɞɧɵɯ ɦɟɬɚɥɥɚɯ c ɭɡɤɢɦɢ ɡɨɧɚɦɢ ɏɚɛɛɚɪɞ ɜ 1964ɝ. ɩɪɟɞ-
ɥɨɠɢɥ ɦɨɞɟɥɶ, ɤɨɬɨɪɚɹ ɜ ɪɟɠɢɦɟ ɫɢɥɶɧɨɣ ɫɜɹɡɢ, ɭɱɢɬɵɜɚɹ ɩɟ-
ɪɟɫɤɨɤɢ ɷɥɟɤɬɪɨɧɨɜ ɧɚ ɫɨɫɟɞɧɢɟ ɚɬɨɦɵ ɢ ɤɭɥɨɧɨɜɫɤɨɟ ɨɬɬɚɥ-
ɤɢɜɚɧɢɟ ɧɚ ɭɡɥɟ, ɩɨɡɜɨɥɢɥɚ ɨɩɢɫɚɬɶ ɩɟɪɟɯɨɞ ɢɡ ɩɪɨɜɨɞɹɳɟɝɨ ɜ
ɞɢɷɥɟɤɬɪɢɱɟɫɤɨɟ ɫɨɫɬɨɹɧɢɟ. ɗɬɚ ɦɨɞɟɥɶ (ɢ ɟɟ ɪɚɫɲɢɪɟɧɧɵɟ
ɚɧɚɥɨɝɢ) ɜ
ɧɚɫɬɨɹɳɟɟ ɜɪɟɦɹ ɫɬɚɥɚ ɩɨɩɭɥɹɪɧɨɣ ɜ ɫɜɹɡɢ ɫ ɢɫɫɥɟ-
ɞɨɜɚɧɢɟɦ ɜɵɫɨɤɨɬɟɦɩɟɪɚɬɭɪɧɵɯ ɫɜɟɪɯɩɪɨɜɨɞɧɢɤɨɜ, ɬɚɤ ɤɚɤ ɜ
ɧɢɯ ɢɦɟɸɬ ɦɟɫɬɨ ɫɢɥɶɧɵɟ ɤɭɥɨɧɨɜɫɤɢɟ ɤɨɪɪɟɥɹɰɢɢ.
8.3.1. Ƚɚɦɢɥɶɬɨɧɢɚɧ ɦɨɞɟɥɢ ɏɚɛɛɚɪɞɚ.
Ɉɫɧɨɜɧɵɟ ɫɜɨɣɫɬɜɚ
Ⱦɥɹ ɜɵɜɨɞɚ ɦɨɞɟɥɢ ɏɚɛɛɚɪɞ ɢɫɯɨɞɢɥ ɢɡ ɫɬɚɧɞɚɪɬɧɨɝɨ
ɝɚɦɢɥɶɬɨɧɢɚɧɚ ɮɟɪɦɢ-ɝɚɡɚ ɫ ɤɭɥɨɧɨɜɫɤɢɦ ɜɡɚɢɦɨɞɟɣɫɬɜɢɟɦ:
Haa
Vaaaa
pp p
p
pp p p p p p p
pp p p
¦
¦
H
VV
V
VV VV
VV
,
'' , ,' '' '
'' '
/.12
121 2 1 2 2 1
121 2
(8.33)
Ʉɭɥɨɧɨɜɫɤɨɟ ɜɡɚɢɦɨɞɟɣɫɬɜɢɟ ɜ (8.33) ɜɵɩɢɫɚɧɨ ɜ ɫɭɳɟɫɬɜɟɧɧɨ
ɛɨɥɟɟ ɨɛɳɟɦ ɜɢɞɟ, ɱɟɦ, ɧɚɩɪɢɦɟɪ, ɦɵ ɪɚɫɫɦɚɬɪɢɜɚɥɢ ɩɪɢ ɢɫ-
ɫɥɟɞɨɜɚɧɢɢ ɦɨɞɟɥɢ ɋɬɨɧɟɪɚ ɜ ɝɥɚɜɟ 6 (ɫɦ. (6.12)). Ɂɞɟɫɶ ɭɱɬɟɧɨ
ɢ ɩɪɹɦɨɟ ɤɭɥɨɧɨɜɫɤɨɟ ɨɬɬɚɥɤɢɜɚɧɢɟ (ɤɚɤ ɜ ɦɨɞɟɥɢ ɋɬɨɧɟɪɚ), ɢ
ɨɛɦɟɧɧɵɟ ɩɪɨɰɟɫɫɵ; ɪɚɫɫɦɚɬɪɢɜɚɸɬɫɹ ɫɢɫɬɟɦɵ ɫ ɭɡɤɢɦɢ ɡɨ-
ɧɚɦɢ (~ 0.1-1 ɷȼ), ɬ.ɟ. ɷɥɟɤɬɪɨɧɵ ɢɦɟɸɬ ɛɨɥɶɲɭɸ ɷɮɮɟɤɬɢɜ-
ɧɭɸ ɦɚɫɫɭ ɢ
ɩɨɱɬɢ ɥɨɤɚɥɢɡɨɜɚɧɵ. ɉɨɷɬɨɦɭ ɯɨɪɨɲɢɦ ɤɜɚɧɬɨ-
ɜɵɦ ɱɢɫɥɨɦ ɹɜɥɹɟɬɫɹ ɧɨɦɟɪ ɭɡɥɚ. ɉɟɪɟɣɞɟɦ ɨɬ ɢɦɩɭɥɶɫɧɨɝɨ
ɩɪɟɞɫɬɚɜɥɟɧɢɹ ɤ ɭɡɟɥɶɧɵɦ ɨɩɟɪɚɬɨɪɚɦ:
a
N
aip
pi
i
VV
oo
¦
1
exp{ }r
i
.
140

Ɂɞɟɫɶ ɩɨɞ “” - ɦɵ ɩɨɧɢɦɚɟɦ ɧɟ ɨɛɹɡɚɬɟɥɶɧɨ ɩɥɨɫɤɢɟ
ɜɨɥɧɵ, ɚ ɜɨɥɧɨɜɵɟ ɮɭɧɤɰɢɢ ȼɚɧɧɶɟ ɜ ɤɪɢɫɬɚɥɥɟ, ɫɨɜɩɚɞɚɸɳɢɟ
ɫ ɭɡɟɥɶɧɵɦɢ ɮɭɧɤɰɢɹɦɢ ɬɨɱɧɨ ɧɚ ɭɡɥɟ ɢ ɢɦɟɸɳɢɟ ɚɫɢɦɬɨɬɚɦɢ
ɩɥɨɫɤɢɟ ɜɨɥɧɵ ɜɞɚɥɢ ɨɬ ɚɬɨɦɚ. Ɉɧɢ ɨɪɬɨɧɨɪɦɢɪɨɜɚɧɵ ɢ ɨɛɪɚ-
ɡɭɸɬ ɩɨɥɧɭɸ ɫɢɫɬɟɦɭ, ɤɚɤ ɢ ɩɥɨɫɤɢɟ ɜɨɥɧɵ. Ɍɨɝɞɚ ɤɢɧɟɬɢɱɟ-
ɫɤɚɹ ɱɚɫɬɶ ɝɚɦɢɥɶɬɨɧɢɚɧɚ ɢɦɟɟɬ ɜɢɞ:
exp{ }ipr
i
oo
Htaa
t
N
iprr rra
kin
ij i j
ij
ij p
p
ij ijB
z
oo o o o
¦
¦
VV
V
V
H
,
,
exp( [ ]) ~ exp( | | ).
1
(8.34)
Ⱥɦɩɥɢɬɭɞɚ ɩɟɪɟɫɤɨɤɚ ɛɵɫɬɪɨ ɡɚɬɭɯɚɟɬ ɜ ɭɡɤɨɡɨɧɧɨɦ ɜɟɳɟɫɬɜɟ
ɫ ɫɢɥɶɧɨ ɥɨɤɚɥɢɡɨɜɚɧɧɵɦɢ ɧɨɫɢɬɟɥɹɦɢ, ɢ ɨɛɵɱɧɨ ɞɨɫɬɚɬɨɱɧɨ
ɭɱɟɫɬɶ ɜ (8.34) ɩɟɪɟɫɤɨɤɢ ɬɨɥɶɤɨ ɧɚ ɛɥɢɠɚɣɲɢɟ ɫɨɫɟɞɢ.
ɉɨɞɫɬɚɜɢɜ ɩɪɟɨɛɪɚɡɨɜɚɧɢɟ ɨɩɟɪɚɬɨɪɨɜ ɤ ɭɡɟɥɶɧɨɦɭ ɜɢ-
ɞɭ ɜ ɩɨɬɟɧɰɢɚɥɶɧɭɸ ɱɚɫɬɶ ɝɚɦɢɥɶɬɨɧɢɚɧɚ, ɩɨɥɭɱɢɦ, ɱɬɨ ɜ
ɭɡɟɥɶɧɨɦ ɩɪɟɞɫɬɚɜɥɟɧɢɢ ɨɧɚ ɢɦɟɟɬ ɫɥɟɞɭɸɳɢɣ ɜɢɞ:
HVaaaa
V
N
V ipr pr pr pr
ijkl i j l k
ijkl
ijkl p p p p
pp p p
ijlk
int
''
'
''
''
''
,
exp[ { }].
oo o o
o
o
o
o
¦
¦
1
2
1
2
12 21
121 2
121 2
VVV V
VV
(8.35)
ɉɨɥɚɝɚɹ, ɱɬɨ ɝɥɚɜɧɵɣ ɜɤɥɚɞ ɞɚɟɬ ɜɡɚɢɦɨɞɟɣɫɬɜɢɟ ɧɚ ɨɞɧɢɯ ɢ
ɬɟɯ ɠɟ ɭɡɥɚɯ ɫ i=j=k=l (V
ijkl
{
V
iiii
= V(|r|=0)=U), ɚ ɧɚ ɛɨɥɶɲɢɯ
ɪɚɫɫɬɨɹɧɢɹɯ V ɦɧɨɝɨ ɦɟɧɶɲɟ, ɩɨɥɭɱɚɟɦ ɨɤɨɧɱɚɬɟɥɶɧɨ ɝɚɦɢɥɶ-
ɬɨɧɢɚɧ ɏɚɛɛɚɪɞɚ
H taa Uaaa a
ij i j
ij
iii i
i
z
¦¦
VV
V
VVVV
V
,
1
2
. (8.36)
Ɂɞɟɫɶ ɩɟɪɜɵɣ ɱɥɟɧ ɝɚɦɢɥɶɬɨɧɢɚɧɚ (ɤɢɧɟɬɢɱɟɫɤɚɹ ɷɧɟɪɝɢɹ) ɨɩɢ-
ɫɵɜɚɟɬ ɩɟɪɟɫɤɨɤɢ ɧɚ ɫɨɫɟɞɧɢɟ ɭɡɥɵ ɫ ɚɦɩɥɢɬɭɞɨɣ t
ij
. ȼɬɨɪɨɣ
ɱɥɟɧ ɨɩɢɫɵɜɚɟɬ ɤɭɥɨɧɨɜɫɤɨɟ ɨɬɬɚɥɤɢɜɚɧɢɟ ɧɚ ɭɡɥɟ ɫ ɩɨɬɟɧɰɢɚ-
ɥɨɦ U ɢ ɭɱɢɬɵɜɚɟɬ, ɱɬɨ ɨɞɧɨɜɪɟɦɟɧɧɨ ɧɚ ɭɡɥɟ ɦɨɝɭɬ ɧɚɯɨɞɢɬɶ-
ɫɹ ɱɚɫɬɢɰɵ ɬɨɥɶɤɨ ɫ ɩɪɨɬɢɜɨɩɨɥɨɠɧɵɦ ɫɩɢɧɨɦ. Ƚɚɦɢɥɶɬɨɧɢɚɧ
141

ɡɚɩɢɫɵɜɚɸɬ ɜ ɛɨɥɟɟ ɭɞɨɛɧɨɣ ɮɨɪɦɟ ɫ ɢɫɩɨɥɶɡɨɜɚɧɢɟɦ ɩɪɢ-
ɛɥɢɠɟɧɢɹ ɛɥɢɠɚɣɲɢɯ ɫɨɫɟɞɟɣ Z
(t
ij
= - t, i,j = Z)
H t aa Unn n aa
ij
ij
i
i
i
ii
z
n
p
¦¦
VV
V
VV
,
,
i
V
. (8.37)
ȼɨ ɜɡɚɢɦɨɞɟɣɫɬɜɭɸɳɟɣ ɱɚɫɬɢ (8.37) ɤɨɷɮɮɢɰɢɟɧɬ 1/2 ɫɤɨɦ-
ɩɟɧɫɢɪɨɜɚɥɫɹ ɡɚ ɫɱɟɬ ɫɭɦɦɢɪɨɜɚɧɢɹ ɩɨ ɫɩɢɧɚɦ. Ɍɚɤɢɦ ɨɛɪɚ-
ɡɨɦ, ɜ ɦɨɞɟɥɢ ɜɫɟɝɨ ɞɜɚ ɩɚɪɚɦɟɬɪɚ: ɦɚɬɪɢɱɧɵɣ ɷɥɟɦɟɧɬ ɩɟɪɟ-
ɫɤɨɤɚ ɧɚ ɫɨɫɟɞɧɢɣ ɭɡɟɥ t ɢ ɤɭɥɨɧɨɜɫɤɨɟ ɨɬɬɚɥɤɢɜɚɧɢɟ ɧɚ ɭɡɥɟ
U. Ȼɨɥɟɟ ɬɨɝɨ, ɟɫɥɢ ɨɬɫɱɢɬɵɜɚɬɶ ɜɫɟ ɷɧɟɪɝɢɢ ɜ ɟɞɢɧɢɰɚɯ t, ɬɨ
ɨɫɬɚɟɬɫɹ ɟɞɢɧɫɬɜɟɧɧɵɣ ɩɚɪɚɦɟɬɪ t/U.
Ɂɧɚɤ ɩɟɪɟɫɤɨɤɚ (ɦɢɧɭɫ) ɜɵɛɢɪɚɟɬɫɹ ɢɡ ɭɞɨɛɫɬɜɚ ɨɬɫɱɟɬɚ
ɩɨɥɭɱɚɸɳɢɯɫɹ ɡɨɧ ɫɢɦɦɟɬɪɢɱɧɨ ɨɬ ɰɟɧɬɪɚ ɡɨɧɵ Ȼɪɢɥɥɸɷɧɚ.
Ɍɚɤɚɹ ɜɨɥɶɧɨɫɬɶ ɜ ɜɵɛɨɪɟ ɡɧɚɤɚ ɫɜɹɡɚɧɚ ɫɨ ɫɥɟɞɭɸɳɢɦ ɫɜɨɣɫɬ-
ɜɨɦ ɝɚɦɢɥɶɬɨɧɢɚɧɚ (8.37): ɡɚɦɟɧɚ t
o
-t ɧɟ ɦɟɧɹɟɬ ɫɩɟɤɬɪ ɦɨɞɟ-
ɥɢ ɏɚɛɛɚɪɞɚ, ɟɫɥɢ ɩɟɪɟɫɤɨɤ ɩɪɨɢɫɯɨɞɢɬ ɬɨɥɶɤɨ ɦɟɠɞɭ ɛɥɢ-
ɠɚɣɲɢɦɢ ɫɨɫɟɞɹɦɢ (ɫɦ. ɡɚɞɚɱɢ ɤ ɩɚɪɚɝɪɚɮɭ).
Ɇɨɠɧɨ ɞɨɤɚɡɚɬɶ ɬɚɤɠɟ, ɱɬɨ ɝɚɦɢɥɶɬɨɧɢɚɧ ɤɨɦɦɭɬɢɪɭɟɬ
ɫ ɨɩɟɪɚɬɨɪɨɦ ɩɨɥɧɨɝɨ ɱɢɫɥɚ ɱɚɫɬɢɰ N ɢ ɩɨɥɧɨɣ ɩɪɨɟɤɰɢɢ ɫɩɢ-
ɧɚ ɧɚ ɨɫɶ z - S
Z
:
N aa S aa aa n n
ii
i
Z
ii
ii
i
i
i
i
n
n
p
p
n
p
¦¦ ¦
VV
V
,( )(
1
2
1
2
), (8.38)
ɬ.ɟ. ɡɚɞɚɱɭ ɦɨɠɧɨ ɪɟɲɚɬɶ ɩɪɢ ɤɨɧɤɪɟɬɧɨɦ ɡɚɩɨɥɧɟɧɢɢ ɢ ɩɪɨ-
ɟɤɰɢɢ ɫɩɢɧɚ ɧɟɡɚɜɢɫɢɦɨ, ɬɚɤ ɤɚɤ ɨɧɢ ɫɨɯɪɚɧɹɸɬɫɹ ɜ ɦɨɞɟɥɢ
ɏɚɛɛɚɪɞɚ.
ɉɭɫɬɶ ɱɢɫɥɨ ɭɡɥɨɜ ɪɚɜɧɨ N
a
. ɉɪɢ ɩɨɥɨɜɢɧɧɨɦ ɡɚɩɨɥɧɟ-
ɧɢɢ, ɬ.ɟ. ɤɨɝɞɚ N=N
a
, ɢ ɛɨɥɶɲɨɦ ɤɭɥɨɧɨɜɫɤɨɦ ɜɡɚɢɦɨɞɟɣɫɬɜɢɢ
U/t>>1 ɜɫɟ ɷɥɟɤɬɪɨɧɵ ɩɪɚɤɬɢɱɟɫɤɢ “ɡɚɩɟɪɬɵ” ɧɚ ɫɜɨɢɯ ɭɡɥɚɯ,
ɨɛɪɚɡɭɹ ɚɧɬɢɮɟɪɪɨɦɚɝɧɢɬɧɨɟ ɭɩɨɪɹɞɨɱɟɧɢɟ:
npnpnpnpnpn
142
ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɝɚɦɢɥɶɬɨɧɢɚɧ ɏɚɛɛɚɪɞɚ ɷɤɜɢɜɚɥɟɧɬɟɧ ɝɟɣɡɟɧ-
ɛɟɪɝɨɜɫɤɨɦɭ ɚɧɬɢɮɟɪɪɨɦɚɝɧɢɬɧɨɦɭ ɝɚɦɢɥɶɬɨɧɢɚɧɭ (ɫɦ. ɫɨɨɬ-
ɜɟɬɫɬɜɭɸɳɭɸ ɡɚɞɚɱɭ ɧɢɠɟ).

Ɂɚɦɟɬɢɦ, ɱɬɨ ɦɨɞɟɥɶ ɏɚɛɛɚɪɞɚ ɫɢɦɦɟɬɪɢɱɧɚ ɨɬɧɨɫɢ-
ɬɟɥɶɧɨ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɷɥɟɤɬɪɨɧ-ɞɵɪɤɚ (a
+
®b, a®b
+
). ɉɨɷɬɨ-
ɦɭ, ɩɨɥɶɡɭɹɫɶ ɫɜɨɣɫɬɜɨɦ (t®-t) ɢ ɷɬɢɦɢ ɩɪɟɨɛɪaɡɨɜɚɧɢɹɦɢ,
ɦɨɠɧɨ ɩɨɤɚɡɚɬɶ ɫɥɟɞɭɸɳɢɟ ɫɜɨɣɫɬɜɚ ɷɧɟɪɝɢɢ ɫɢɫɬɟɦɵ.
ɉɭɫɬɶ
Ɇ
- ɱɢɫɥɨ ɫɩɢɧɨɜ ɜɜɟɪɯ;
Ɇ
’
- ɱɢɫɥɨ ɫɩɢɧɨɜ ɜɧɢɡ,
M+M’=N. Ɍɨɝɞɚ ɢɦɟɸɬ ɦɟɫɬɨ ɫɥɟɞɭɸɳɢɟ ɫɨɨɬɧɨɲɟɧɢɹ (ɜɩɟɪ-
ɜɵɟ ɩɨɥɭɱɟɧɧɵɟ Ʌɢɛɨɦ ɢ ȼɭ ɜ 1968 ɝ. [19]):
E(M,M’, U) = -(N
a
-M-M’)U + E(N
a
-M, N
a
-M’,U),
E(M,M’, U) = MU + E(M, N
a
-M’,-U), (8.39)
E(M,M’, U) = M’U + E(N
a
-M, M’,-U).
ɉɨɥɭɱɢɦ, ɧɚɩɪɢɦɟɪ, ɩɟɪɜɨɟ ɢɡ ɫɨɨɬɧɨɲɟɧɢɣ (8.39). ɉɨɞɫɬɚɜɢɜ
ɜ (8.37) ɞɵɪɨɱɧɵɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ a
+
®b, a®b
+
, ɢɦɟɟɦ:
H t bb Ubbbb
UUbb Ubb
ij
ij
ii
ii
i
i
ii
ii
ii
z
n
n
p
p
n
n
p
p
¦¦
¦¦¦
VV
V
,
.
M
M
(8.40)
ɍɱɢɬɵɜɚɹ, ɱɬɨ ɱɢɫɥɨ ɞɵɪɨɤ ɫɨ ɫɩɢɧɨɦ ɜɜɟɪɯ
bb N M
ii
i
a
n
n
¦
,
ɚ ɱɢɫɥɨ ɞɵɪɨɤ ɫɨ ɫɩɢɧɨɦ ɜɧɢɡ
bb N M
ii
i
a
p
p
¦
',
ɩɨɥɭɱɚɟɦ ɩɟɪɜɨɟ ɫɨɨɬɧɨɲɟɧɢɟ (8.39) (E=<H>).
Ɂɚɞɚɱɢ
8.3.1.
1. Ⱦɨɤɚɡɚɬɶ ɨɩɟɪɚɬɨɪɧɵɟ ɬɨɠɞɟɫɬɜɚ:
exp{ } exp{ } exp( )
iaa a iaa a i
ii i ii i
MM
VV V VV V
,
exp{ } exp{ } exp( )
iaa a iaa a i
ii i ii i
MM
VV V VV V
.
ɍɤɚɡɚɧɢɟ
: ɩɪɨɞɢɮɮɟɪɟɧɰɢɪɨɜɚɬɶ ɥɟɜɭɸ ɱɚɫɬɶ ɬɨɠɞɟɫɬɜ
ɩɨ ɩɟɪɟɦɟɧɧɨɣ
I
.
143
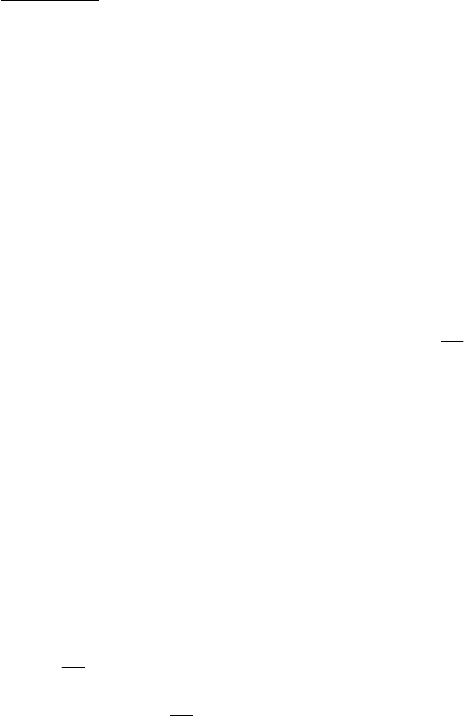
8.3.1.2. ɉɨɤɚɡɚɬɶ, ɱɬɨ ɡɚɦɟɧɚ
t
o
-t ɧɟ ɦɟɧɹɟɬ ɫɩɟɤɬɪ
ɦɨɞɟɥɢ ɏɚɛɛɚɪɞɚ, ɟɫɥɢ ɩɟɪɟɫɤɨɤ ɩɪɨɢɫɯɨɞɢɬ ɬɨɥɶɤɨ ɦɟɠɞɭ
ɛɥɢɠɚɣɲɢɦɢ ɫɨɫɟɞɹɦɢ.
Ɋɟɲɟɧɢɟ
. Ɋɚɡɨɛɴɟɦ ɭɡɥɵ ɧɚ ɞɜɟ ɩɨɞɪɟɲɟɬɤɢ
Ⱥ
ɢ
Ȼ
, ɜɥɨ-
ɠɟɧɧɵɟ ɨɞɧɚ ɜ ɞɪɭɝɭɸ, ɬɚɤ ɱɬɨ ɛɥɢɠɚɣɲɢɦ ɫɨɫɟɞɨɦ ɭɡɥɚ
Ⱥ
ɨɛɹɡɚɬɟɥɶɧɨ ɹɜɥɹɟɬɫɹ ɭɡɟɥ
Ȼ
ɢ ɧɚɨɛɨɪɨɬ. Ⱦɥɹ ɜɫɟɯ ɭɡɥɨɜ
Ⱥ
ɫɞɟ-
ɥɚɟɦ ɭɧɢɬɚɪɧɨɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɟ
Ui
,
aa
i
A
i
A
i
A
¦¦
exp{ }
S
VV
V
ɤɨɬɨɪɨɟ ɦɟɧɹɟɬ ɡɧɚɤ ɨɩɟɪɚɬɨɪɨɜ
Ⱥ
:
. ɗɬɨ
ɫɥɟɞɭɟɬ ɢɡ ɨɩɟɪɚɬɨɪɧɨɝɨ ɬɨɠɞɟɫɬɜɚ:
aaa
iiii
VVV
o o, a
V
M
exp{ } exp{ } exp( )
ia a a ia a a i
ii i ii i
MM
VV V VV V
,
ɤɨɬɨɪɨɟ ɧɟɫɥɨɠɧɨ ɞɨɤɚɡɚɬɶ ɧɟɩɨɫɪɟɞɫɬɜɟɧɧɵɦ ɞɢɮɮɟɪɟɧɰɢɪɨ-
ɜɚɧɢɟɦ ɩɨ ɩɚɪɚɦɟɬɪɭ
M
(ɫɦ.ɩɪɟɞɵɞɭɳɭɸ ɡɚɞɚɱɭ). ɉɪɢɦɟɧɢɦ
ɨɩɟɪɚɬɨɪ U ɤ ɝɚɦɢɥɶɬɨɧɢɚɧɭ ɏɚɛɛɚɪɞɚ:
U
H
U
1
. Ɋɚɫɫɦɨɬɪɢɦ
ɩɟɪɟɫɤɨɤɨɜɵɣ ɱɥɟɧ. Ɍɨɝɞɚ ɡɚɦɟɬɢɦ, ɱɬɨ ɜɫɟɝɞɚ ɢɦɟɟɦ ɜ ɧɟɦ
ɤɨɦɛɢɧɚɰɢɸ a
+A
a
Ȼ
ɢɥɢ a
+Ȼ
ɚ
A
. Ɉɱɟɜɢɞɧɨ, ɱɬɨ ɭɧɢɬɚɪɧɨɟ ɩɪɟ-
ɨɛɪɚɡɨɜɚɧɢɟ, ɢɡɦɟɧɹɹ ɡɧɚɤ ɬɨɥɶɤɨ ɨɩɟɪɚɬɨɪɚ Ⱥ, ɢɡɦɟɧɢɬ ɢ ɜɟɫɶ
ɡɧɚɤ ɩɟɪɟɞ ɱɥɟɧɨɦ. Ʌɟɝɤɨ ɩɨɧɹɬɶ, ɱɬɨ ɜ ɤɭɥɨɧɨɜɫɤɨɦ ɱɥɟɧɟ
ɱɢɫɥɨ ɢɡɦɟɧɟɧɢɣ ɡɧɚɤɨɜ ɜɫɟɝɞɚ ɱɟɬɧɨ:
U
-1
a
+A
a
A
a
+A
a
A
U=U
-1
a
+A
UU
-1
a
A
UU
-1
a
+A
UU
-1
a
A
U=
=a
+A
a
A
a
+A
a
A
.
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɜɡɚɢɦɨɞɟɣɫɬɜɭɸɳɢɣ ɱɥɟɧ ɢɧɜɚɪɢɚɧɬɟɧ ɨɬɧɨ-
ɫɢɬɟɥɶɧɨ ɬɚɤɨɝɨ ɭɧɢɬɚɪɧɨɝɨ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ. Ⱥ ɬɚɤ ɤɚɤ
U HUU U U EUU U EU U
UHU E U U
11 11 1
11
\\
\
<<<,,
\
ɬɨ ɫɩɟɤɬɪ E ɧɟ ɢɡɦɟɧɢɥɫɹ , ɧɨ ɩɪɢ ɷɬɨɦ t ɢɡɦɟɧɢɥɫɹ ɧɚ -t, ɱɬɨ
ɢ ɬɪɟɛɨɜɚɥɨɫɶ ɞɨɤɚɡɚɬɶ.
8.3.1.
3. ɉɨɤɚɡɚɬɶ, ɱɬɨ ɝɚɦɢɥɶɬɨɧɢɚɧ ɏɚɛɛɚɪɞɚ (8.37)
ɤɨɦɦɭɬɢɪɭɟɬ ɫ ɨɩɟɪɚɬɨɪɨɦ ɩɨɥɧɨɝɨ ɱɢɫɥɚ ɱɚɫɬɢɰ ɢ ɩɨɥɧɨɣ
ɩɪɨɟɤɰɢɢ ɫɩɢɧɚ ɧɚ ɨɫɶ z.
144

8.3.1.4. ɉɭɫɬɶ N
a
- ɱɢɫɥɨ ɭɡɥɨɜ; M - ɱɢɫɥɨ ɫɩɢɧɨɜ ɜɜɟɪɯ;
M’ - ɱɢɫɥɨ ɫɩɢɧɨɜ ɜɧɢɡ; N= M+M’ - ɱɢɫɥɨ ɷɥɟɤɬɪɨɧɨɜ. Ⱦɨɤɚ-
ɡɚɬɶ ɫɥɟɞɭɸɳɢɟ ɫɨɨɬɧɨɲɟɧɢɹ ɞɥɹ ɷɧɟɪɝɢɢ ɜ ɦɨɞɟɥɢ ɏɚɛɛɚɪɞɚ:
E(M,M’,U) = MU + E(M, N
a
-M’,-U),
E(M,M’ U) = M’U + E(N
a
-M, M’,-U).
ɍɤɚɡɚɧɢɟ
: ɩɟɪɟɣɬɢ ɤ ɞɵɪɨɱɧɨɦɭ ɩɪɟɞɫɬɚɜɥɟɧɢɸ ɞɥɹ
ɷɥɟɤɬɪɨɧɨɜ ɫɨ ɫɩɢɧɨɦ ɜɧɢɡ ɜ ɩɟɪɜɨɦ ɫɥɭɱɚɟ ɢ ɫɨ ɫɩɢɧɨɦ ɜɜɟɪɯ
ɜɨ ɜɬɨɪɨɦ.
8.3.1.
5. ɑɟɦɭ ɪɚɜɧɚ ɷɧɟɪɝɢɹ ɨɫɧɨɜɧɨɝɨ ɫɨɫɬɨɹɧɢɹ ɦɨɞɟ-
ɥɢ ɏɚɛɛɚɪɞɚ ɩɪɢ ɩɨɥɨɜɢɧɧɨɦ ɡɚɩɨɥɧɟɧɢɢ N = N
a
ɢ ɜ ɩɪɟɞɟɥɟ
U
of
?
8.3.1.
6. Ɋɚɫɫɱɢɬɚɬɶ ɱɢɫɥɨ ɜɨɡɦɨɠɧɵɯ ɭɡɟɥɶɧɵɯ ɫɨɫɬɨɹ-
ɧɢɣ (ɪɚɡɦɟɪ ɝɢɥɶɛɟɪɬɨɜɚ ɩɪɨɫɬɪɚɧɫɬɜɚ) ɜ ɦɨɞɟɥɢ ɏɚɛɛɚɪɞɚ
ɩɪɢ:
1)ɱɢɫɥɟ ɭɡɥɨɜ N
a
=12, ɱɢɫɥɟ ɷɥɟɤɬɪɨɧɨɜ ɫɨ ɫɩɢɧɨɦ ɜɜɟɪɯ
M=4, ɫɨ ɫɩɢɧɨɦ ɜɧɢɡ M’=3;
2) N
a
=12, M=3, M’=3;
3) N
a
=8, M=4, M’=4;
4) N
a
=8, M=2, M’=3.
8.3.1.
7. ɉɨɤɚɡɚɬɶ ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɶ ɚɧɬɢɮɟɪɪɨɦɚɝɧɢɬɧɨɣ
ɦɨɞɟɥɢ Ƚɟɣɡɟɧɛɟɪɝɚ ɢ ɦɨɞɟɥɢ ɏɚɛɛɚɪɞɚ ɜɛɥɢɡɢ ɩɨɥɨɜɢɧɧɨɝɨ
ɡɚɩɨɥɧɟɧɢɹ ɩɪɢ U/t>>1.
Ɋɟɲɟɧɢɟ
. Ɋɚɡɞɟɥɢɦ ɝɚɦɢɥɶɬɨɧɢɚɧ ɏɚɛɛɚɪɞɚ ɧɚ ɧɟɫɤɨɥɶ-
ɤɨ ɫɥɚɝɚɟɦɵɯ:
HT T T V
dhmix
, (8.41)
ɝɞɟ
145
146
..),VUnnTtnaankc
Tt naa n kc
Tt naan
naa n kc
i
i
i
d i ijj
ij
hiijj
ij
mix i i j j
ij
iij j
n
p
z
z
z
¦¦
¦
¦
,(
{( ) ( ) . },
{( )
().}.
,
,
,
VV V V
V
VVV V
V
VVV V
V
VV V V
11
1
1
(8.42)
T
d
ɨɩɢɫɵɜɚɟɬ ɤɨɪɪɟɥɢɪɨɜɚɧɧɵɟ ɩɟɪɟɫɤɨɤɢ ɫ ɭɡɥɚ ɧɚ ɭɡɟɥ ɫɨ
ɫɩɢɧɨɦ
V
, ɤɨɝɞɚ ɭɡɥɵ ɡɚɧɹɬɵ ɷɥɟɤɬɪɨɧɚɦɢ ɫ ɩɪɨɬɢɜɨɩɨɥɨɠ-
ɧɵɦ ɫɩɢɧɨɦ -
V
, ɱɥɟɧ T
h
, ɧɚɨɛɨɪɨɬ, ɨɩɢɫɵɜɚɟɬ ɩɟɪɟɫɤɨɤɢ ɫ ɭɡ-
ɥɚɦɢ, ɧɟɡɚɩɨɥɧɟɧɧɵɦɢ ɷɥɟɤɬɪɨɧɚɦɢ ɫ ɩɪɨɬɢɜɨɩɨɥɨɠɧɵɦ ɫɩɢ-
ɧɨɦ, ɚ T
mix
- ɩɪɨɰɟɫɫɵ ɩɟɪɟɫɤɨɤɚ, ɤɨɝɞɚ ɥɢɛɨ ɨɞɢɧ, ɥɢɛɨ ɞɪɭ-
ɝɨɣ (ɧɨ ɧɟ ɞɜɚ ɨɞɧɨɜɪɟɦɟɧɧɨ) ɭɡɥɚ, ɭɱɚɫɬɜɭɸɳɢɯ ɜ ɩɟɪɟɫɤɨɤɟ,
ɡɚɧɹɬɵ ɷɥɟɤɬɪɨɧɨɦ ɫ ɩɪɨɬɢɜɨɩɨɥɨɠɧɵɦ ɫɩɢɧɨɦ.
ȼ ɩɪɟɞɟɥɟ U/t >>1 ɫɚɦɵɣ ɦɚɥɵɣ ɜɤɥɚɞ ɞɚɟɬ ɱɥɟɧ T
d
, ɬɚɤ ɤɚɤ
ɷɬɨɬ ɩɪɨɰɟɫɫ ɫɜɹɡɚɧ ɫ ɛɨɥɶɲɨɣ ɞɨɛɚɜɤɨɣ ɤ ɷɧɟɪɝɢɢ ɷɥɟɤɬɪɨɧɚ
~U.
Ɋɚɫɫɦɨɬɪɢɦ ɧɟɤɨɬɨɪɨɟ ɭɧɢɬɚɪɧɨɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɟ ɝɚ-
ɦɢɥɶɬɨɧɢɚɧɚ, ɧɟ ɦɟɧɹɸɳɟɟ ɟɝɨ ɫɩɟɤɬɪɚ:
HiSH
eff
exp( ) exp( )iS .
ɉɪɟɞɩɨɥɨɠɢɦ, ɱɬɨ S ɦɚɥɨ ɩɨ ɩɚɪɚɦɟɬɪɭ t/U, ɢ ɜ ɩɟɪɜɨɦ ɩɪɢ-
ɛɥɢɠɟɧɢɢ:
HiSHiSHiS
eff
()() [,11 H ]
ix
. (8.43)
Ɉɩɪɟɞɟɥɢɦ ɷɮɮɟɤɬɢɜɧɵɣ ɝɚɦɢɥɶɬɨɧɢɚɧ ɢ ɭɧɢɬɚɪɧɨɟ
ɩɪɟɨɛɪɚɡɨɜɚɧɢɟ. ɂɳɟɦ S, ɭɞɨɜɥɟɬɜɨɪɹɸɳɟɟ ɫɨɨɬɧɨɲɟɧɢɸ
iS T T V T
dh m
[, ] . (8.44)
Ɉɬɫɸɞɚ
. (8.45) HTTViST
eff d h mix
[, ]
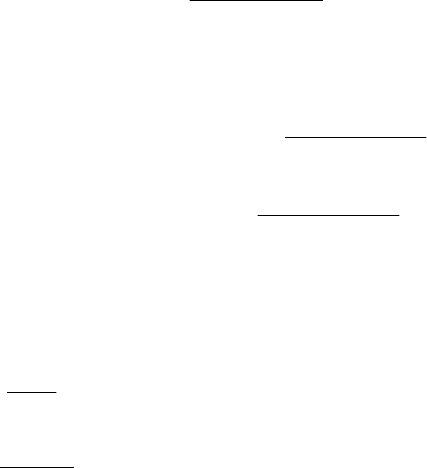
ɑɥɟɧɨɦ V ɦɨɠɧɨ ɩɪɟɧɟɛɪɟɱɶ, ɬɚɤ ɤɚɤ ɩɪɢ ɛɨɥɶɲɢɯ U ɜɟɪɨɹɬ-
ɧɨɫɬɶ ɧɚɯɨɠɞɟɧɢɹ ɧɚ ɨɞɧɨɦ ɭɡɥɟ ɞɜɭɯ ɷɥɟɤɬɪɨɧɨɜ ɦɚɥɚ. ɉɨ
ɷɬɨɣ ɠɟ ɩɪɢɱɢɧɟ ɩɪɟɧɟɛɪɟɠɟɦ ɢ T
d
. Ɍɨɝɞɚ ɢɦɟɟɦ
HTiST
eff h mix
#[ , ]. (8.46)
ɉɪɟɞɩɨɥɨɠɢɦ, ɱɬɨ |n> - ɫɨɛɫɬɜɟɧɧɵɟ ɜɨɥɧɨɜɵɟ ɮɭɧɤɰɢɢ ɨɩɟ-
ɪɚɬɨɪɚ T
d
+T
h
+V, ɚ
H
n
- ɫɨɛɫɬɜɟɧɧɵɟ ɷɧɟɪɝɢɢ. Ɍɨɝɞɚ ɢɡ (8.44)
ɩɨɥɭɱɚɟɦ:
inST T Vm inT T VSm
nT m
inSm inSm nT m
nSm
nT m
i
dh dh
mix
mnmix
mix
mn
!!
!
! ! !
!
!
|( )| |( )|
||
|| || | |
||
||
()
.
HH
HH
(8.47)
ɉɪɨɫɭɦɦɢɪɭɟɦ ɩɨɫɥɟɞɧɟɟ ɜɵɪɚɠɟɧɢɟ ɜ (8.47) ɢ ɜɨɫɩɨɥɶɡɭɟɦɫɹ
ɩɨɥɧɨɬɨɣ ɫɨɛɫɬɜɟɧɧɵɯ ɮɭɧɤɰɢɣ, ɬɨɝɞɚ ɞɥɹ S ɩɨɥɭɱɢɦ
||| ||
||
()
|,
|| |
||
()
|.
,,
,
nnSmm n
nT m
i
m
nn S n
nT m
i
m
nm
mix
mn
nm
n
mix
mn
nm
! ! !
!
! !
!
¦¦
¦¦
HH
HH
(8.48)
ȼɛɥɢɡɢ ɩɨɥɨɜɢɧɧɨɝɨ ɡɚɩɨɥɧɟɧɢɹ ɩɪɢ ɛɨɥɶɲɨɦ U ɥɸɛɵɟ ɜɨɡ-
ɛɭɠɞɟɧɢɹ ɫɢɫɬɟɦɵ ɧɚɞ ɨɫɧɨɜɧɵɦ ɫ ɬɨɱɧɨɫɬɶɸ ɞɨ t/U ɛɭɞɭɬ
H
m
-
H
n
=
r
U. Ɉɬɫɸɞɚ
S
iU
nnTmm
iU
nnTmm
nm
mix
nm
mix
!!
! !
!
¦
¦
1
1
1
2
||| |
||| |
!
.
(8.49)
Ɂɞɟɫɶ T
1
mix
ɢ T
2
mix
- ɱɚɫɬɢ ɨɩɟɪɚɬɨɪɚ T
mix
, ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ
ɭɜɟɥɢɱɟɧɢɸ (ɭɦɟɧɶɲɟɧɢɸ) ɷɧɟɪɝɢɢ.
147
148
V
)
Ɉɩɪɟɞɟɥɢɦ ɩɪɚɜɢɥɶɧɨ ɡɧɚɤɢ ɜ ɜɵɪɚɠɟɧɢɢ (8.49). ȼɜɵ-
ɪɚɠɟɧɢɢ ɞɥɹ T
mix
(8.42) ɩɟɪɜɨɟ ɫɥɚɝɚɟɦɨɟ
[~ ] ɩɨɧɢɠɚɟɬ ɷɧɟɪɝɢɸ ɧɚ U (ɬ.ɟ. ɫɨɜ-
ɩɚɞɚɟɬ ɫ T
()1
naan
iijj
VVV
2
mix
), ɬɚɤ ɤɚɤ ɷɥɟɤɬɪɨɧ ɭɯɨɞɢɬ ɫ ɞɜɚɠɞɵ ɡɚɩɨɥɧɟɧɧɨ-
ɝɨ ɭɡɥɚ j ɧɚ ɩɭɫɬɨɣ ɭɡɟɥ i. ȼɬɨɪɨɟ ɫɥɚɝɚɟɦɨɟ
[],ɧɚɨɛɨɪɨɬ, ɩɨɜɵɲɚɟɬ ɷɧɟɪɝɢɸ ɧɚ U
(ɬ.ɟ. ɫɨɜɩɚɞɚɟɬ ɫ T
naa n
iij j
VV V V
(1
1
mix
). ɇɟɫɥɨɠɧɨ ɞɨɤɚɡɚɬɶ, ɱɬɨ ɷɪɦɢɬɨɜɨ-
ɫɨɩɪɹɠɟɧɧɚɹ ɱɚɫɬɶ T
mix
ɫɨɜɩɚɞɚɟɬ ɫ ɩɟɪɜɨɣ ɫ ɬɨɱɧɨɫɬɶɸ ɞɨ ɡɚ-
ɦɟɧɵ T
1
<->T
2
ɢ ɞɨɩɨɥɧɹɟɬ ɞɨ ɩɨɥɧɨɝɨ ɫɭɦɦɢɪɨɜɚɧɢɹ
(n<m + n>m = n,m) ɜ (8.49). ɉɨɷɬɨɦɭ ɜ ɢɬɨɝɟ ɢɡ (8.49) ɢɦɟɟɦ,
ɢɫɩɨɥɶɡɭɹ ɩɨɥɧɨɬɭ ɜɨɥɧɨɜɵɯ ɮɭɧɤɰɢɣ:
S
it
U
naa n
naan
iij j
ij
iijj
z
¦
{(
() }.
,
VV V V
V
VVV V
1
1
)
,
,
(8.50)
ɍɱɢɬɵɜɚɹ (8.46), ɧɚɣɞɟɦ ɤɨɦɦɭɬɚɬɨɪ i[S, T
mix
]. ȿɫɥɢ ɨɛɨɡɧɚ-
ɱɢɬɶ
Atnaa n
Bt naan
iij j
ij
i ijj
ij
z
z
¦
¦
VV V V
V
VVVV
V
()
()
,
,
1
1
(8.51)
ɬɨ ɫɨɝɥɚɫɧɨ (8.42) ɢ (8.50) ɧɚɯɨɞɢɦ:
TABS
i
U
AB
iST
U
AB
t
U
naa n n aan
mix
mix
iij j
ij
i ijj
ij
z
z
¦¦
,(),
[, ] [, ]
[(),()
,,
2
2
11
2
VV V V
V
VVVV
V
].
(8.52)
ȼɜɟɞɟɦ ɬɟɩɟɪɶ ɫɩɢɧɨɜɵɟ ɨɩɟɪɚɬɨɪɵ ɫ ɩɨɥɧɨɣ ɩɪɨɟɤɰɢɟɣ ɫɩɢɧɚ
1/2 ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ:

SaaSaaS nn
SSiSSSiS
i
i
i
i
i
i
i
Z
i
i
ii
X
i
Y
ii
X
i
Y
n
p
p
nn
p
,,(
,.
1
2
),
(8.53)
Ʌɟɝɤɨ ɩɪɨɜɟɪɢɬɶ, ɱɬɨ ɜɜɟɞɟɧɧɵɟ ɬɚɤɢɦ ɨɛɪɚɡɨɦ ɨɩɟɪɚɬɨɪɵ
ɹɜɥɹɸɬɫɹ ɨɛɵɱɧɵɦɢ ɨɩɟɪɚɬɨɪɚɦɢ ɫɩɢɧɚ 1/2, ɩɨɞɱɢɧɹɸɬɫɹ
ɜɫɟɦ ɤɨɦɦɭɬɚɰɢɨɧɧɵɦ ɫɨɨɬɧɨɲɟɧɢɹɦ ɢ ɜɵɪɚɠɚɸɬɫɹ ɱɟɪɟɡ
ɦɚɬɪɢɰɵ ɉɚɭɥɢ: S
X
= 1/2
V
X
, S
Y
= 1/2
V
Y
, S
Z
= 1/2
V
Z
.
ɂɫɩɨɥɶɡɭɹ (8.53), ɩɨɫɥɟ ɝɪɨɦɨɡɞɤɢɯ ɩɪɟɨɛɪɚɡɨɜɚɧɢɣ ɢɡ
(8.52) ɩɨɥɭɱɚɟɦ:
iS T
t
U
SS nn
mix i j i j
ij
[, ] ( )
oo
¦
21
4
2
. (8.54)
Ɉɤɨɧɱɚɬɟɥɶɧɨ, ɭɱɢɬɵɜɚɹ (8.46), ɧɚɯɨɞɢɦ ɷɮɮɟɤɬɢɜɧɵɣ ɝɚ-
ɦɢɥɶɬɨɧɢɚɧ
Ht naankc
t
U
SS nn
eff i i j j
ij
ij ij
ij
z
oo
¦
¦
{( ) ( ) . }
().
,
11
21
4
2
VVV V
V
(8.55)
Ƚɚɦɢɥɶɬɨɧɢɚɧ (8.55) - ɩɪɟɞɟɥɶɧɵɣ ɫɥɭɱɚɣ ɝɚɦɢɥɶɬɨɧɢɚ-
ɧɚ ɏɚɛɛɚɪɞɚ ɩɪɢ ɛɨɥɶɲɢɯ U ɜɛɥɢɡɢ ɩɨɥɨɜɢɧɧɨɝɨ ɡɚɩɨɥɧɟɧɢɹ.
Ɋɨɜɧɨ ɩɪɢ ɩɨɥɨɜɢɧɧɨɦ ɡɚɩɨɥɧɟɧɢɢ, ɤɨɝɞɚ ɧɚ ɤɚɠɞɵɣ ɭɡɟɥ
ɩɪɢɯɨɞɢɬɫɹ ɨɞɢɧ ɷɥɟɤɬɪɨɧ, ɩɟɪɟɫɤɨɤɨɜɵɣ ɱɥɟɧ ɡɚɧɭɥɹɟɬɫɹ, ɢ
ɦɨɞɟɥɶ (8.55) ɫɬɚɧɨɜɢɬɫɹ ɚɧɬɢɮɟɪɪɨɦɚɝɧɢɬɧɨɣ ɦɨɞɟɥɶɸ Ƚɟɣ-
ɡɟɧɛɟɪɝɚ (ɫ ɬɨɱɧɨɫɬɶɸ ɞɨ ɧɟɫɭɳɟɫɬɜɟɧɧɨɣ ɩɨɫɬɨɹɧɧɨɣ):
H
t
U
SS
eff i j
ij
oo
¦
21
4
2
() (8.56)
ɫ ɷɮɮɟɤɬɢɜɧɵɦ ɨɛɦɟɧɧɵɦ ɢɧɬɟɝɪɚɥɨɦ J = t
2
/U. Ɂɚɦɟɬɢɦ, ɱɬɨ
ɜɟɥɢɱɢɧɚ J ~ 0.1-0.5 ɷȼ (ɬɚɤ ɤɚɤ t ~ 1 ɷȼ, U ~ 3-10 ɷȼ), ɱɬɨ
ɜɩɨɥɧɟ ɫɨɝɥɚɫɭɟɬɫɹ ɫ ɨɰɟɧɤɚɦɢ ɨɛɦɟɧɧɨɝɨ ɢɧɬɟɝɪɚɥɚ. Ɍɚɤɢɦ
ɨɛɪɚɡɨɦ, ɚɧɬɢɮɟɪɪɨɦɚɝɧɢɬɧɵɣ ɝɚɦɢɥɶɬɨɧɢɚɧ Ƚɟɣɡɟɧɛɟɪɝɚ ɹɜ-
ɥɹɟɬɫɹ ɩɪɟɞɟɥɶɧɵɦ ɫɥɭɱɚɟɦ ɦɨɞɟɥɢ ɏɚɛɛɚɪɞɚ ɩɪɢ ɛɨɥɶɲɢɯ U
ɢ ɩɨɥɨɜɢɧɧɨɦ ɡɚɩɨɥɧɟɧɢɢ.
149
