Елесин В.Ф., Кашурников В.А. Физика фазовых переходов
Подождите немного. Документ загружается.

ɉɭɫɬɶ ɫɧɚɱɚɥɚ ɜɟɳɟɫɬɜɨ ɧɚɯɨɞɢɬɫɹ ɜ ɫɨɫɬɨɹɧɢɢ ɢɡɨɥɹ-
ɬɨɪɚ. ȼɚɥɟɧɬɧɵɣ ɷɥɟɤɬɪɨɧ ɞɜɢɠɟɬɫɹ ɜɨɤɪɭɝ ɫɜɨɟɝɨ ɢɨɧɚ, ɧɚɯɨ-
ɞɹɫɶ ɜ ɟɝɨ ɤɭɥɨɧɨɜɫɤɨɦ ɩɨɥɟ, ɫ ɷɧɟɪɝɢɟɣ:
E
e
r
p
m
22
2
. (8.1)
ɇɟɫɥɨɠɧɨ ɢɡ ɫɨɨɬɧɨɲɟɧɢɹ ɧɟɨɩɪɟɞɟɥɟɧɧɨɫɬɢ ɨɰɟɧɢɬɶ ɤɨɨɪɞɢ-
ɧɚɬɧɭɸ ɡɚɜɢɫɢɦɨɫɬɶ ɤɢɧɟɬɢɱɟɫɤɨɝɨ ɱɥɟɧɚ ɜ ɷɧɟɪɝɢɢ
, ɨɬɤɭɞɚpr p r~~! /!
E
e
r
m
r
22
2
2
!
. (8.2)
Ɇɢɧɢɦɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ ɷɧɟɪɝɢɢ ɜ ɪɚɜɧɨɜɟɫɢɢ ɞɚɟɬ ɭɫɥɨɜɢɟ ɧɚ
ɛɨɪɨɜɫɤɢɣ ɪɚɞɢɭɫ ɨɪɛɢɬɵ a
B
:
w
w
E
r
rr
me
a
B
0
0
2
2
!
. (8.3)
ȼ ɫɜɨɸ ɨɱɟɪɟɞɶ ɡɧɚɱɟɧɢɟ ɷɧɟɪɝɢɢ ɜ ɬɨɱɤɟ ɦɢɧɢɦɭɦɚ
E
e
a
B
2
2
0. (8.4)
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɷɥɟɤɬɪɨɧ ɧɚɯɨɞɢɬɫɹ ɜ ɫɜɹɡɚɧɧɨɦ ɫɨɫɬɨɹɧɢɢ, ɧɟ
ɩɪɨɜɨɞɢɬ ɬɨɤ, ɢ ɫɨɫɬɨɹɧɢɟ - ɢɡɨɥɹɬɨɪ.
Ɍɟɩɟɪɶ ɭɱɬɟɦ, ɱɬɨ ɜ ɷɥɟɤɬɪɨɧɧɨɦ ɝɚɡɟ ɤɭɥɨɧɨɜɫɤɨɟ
ɜɡɚɢɦɨɞɟɣɫɬɜɢɟ ɫɢɥɶɧɨ ɷɤɪɚɧɢɪɨɜɚɧɨ. ɗɬɨ ɦɨɠɧɨ ɩɨɥɭɱɢɬɶ ɢɡ
ɫɥɟɞɭɸɳɢɯ ɫɨɨɛɪɚɠɟɧɢɣ.
Ɋɚɫɫɦɨɬɪɢɦ ɫɥɚɛɵɣ ɩɨɬɟɧɰɢɚɥ e
I
, ɩɪɢɥɨɠɟɧɧɵɣ ɤ ɫɢɫ-
ɬɟɦɟ ɷɥɟɤɬɪɨɧɨɜ. Ɋɚɫɫɱɢɬɚɟɦ ɨɬɤɥɢɤ ɧɚ ɧɟɝɨ ɷɥɟɤɬɪɨɧɧɨɝɨ ɝɚ-
ɡɚ. ɉɭɫɬɶ ɩɪɢɥɨɠɟɧɧɵɣ ɩɨɬɟɧɰɢɚɥ ɢɧɞɭɰɢɪɭɟɬ ɩɨɩɪɚɜɤɭ ɤ
ɩɥɨɬɧɨɫɬɢ ɷɥɟɤɬɪɨɧɨɜ
GU
= e
IU
(E
f
), ɝɞɟ
U
(E
f
) - ɩɥɨɬɧɨɫɬɶ ɫɨ-
ɫɬɨɹɧɢɣ ɧɚ ɭɪɨɜɧɟ Ɏɟɪɦɢ. Ⱦɟɣɫɬɜɢɬɟɥɶɧɨ:
130

GU
I
EH I P EH P
I
w
wH
IGH IU
V
I
VV
®
¯
½
¾
¿
|
|
¦
¦¦
o
ne n
e
e
f
eE e
kk
k
k
k
k
ff
k
TE
f
() ()
exp[ ( )] exp[ ( )]
() (
0
1
1
1
1
0
E ).
M
(8.5)
Ɋɚɫɫɦɨɬɪɢɦ ɭɪɚɜɧɟɧɢɟ ɉɭɚɫɫɨɧɚ
2
00
4
ISUGUUG
er( ), ( ). (8.6)
ɉɟɪɟɯɨɞɹ ɤ ɮɭɪɶɟ-ɤɨɦɩɨɧɟɧɬɚɦ
I
()rdq
iq r
q
e
o
oo
³
3
, (8.7)
ɧɚɯɨɞɢɦ ɢɡ (8.5), (8.6)
I
S
SU
q
D
D
f
e
qr
r
eE
4
1
1
4
22
2
2
,
()
. (8.8)
Ɂɞɟɫɶ r
D
- ɞɟɛɚɟɜɫɤɢɣ ɪɚɞɢɭɫ ɷɤɪɚɧɢɪɨɜɚɧɢɹ, ɯɚɪɚɤɬɟɪɢɡɭɸ-
ɳɢɣ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɵɣ ɦɚɫɲɬɚɛ ɤɭɥɨɧɨɜɫɤɨɝɨ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ
ɜ ɷɥɟɤɬɪɨɧɧɨɦ ɝɚɡɟ. Ⱦɟɣɫɬɜɢɬɟɥɶɧɨ, ɩɨɥɭɱɢɦ ɤɨɨɪɞɢɧɚɬɧɭɸ
ɡɚɜɢɫɢɦɨɫɬɶ ɩɨɬɟɧɰɢɚɥɚ
IS
()
exp[ ]
exp[ / ]
redq
iqr
qr
e
rr
r
D
D
o
oo
³
4
3
22
. (8.9)
Ⱦɟɛɚɟɜɫɤɢɣ ɪɚɞɢɭɫ ɷɤɪɚɧɢɪɨɜɚɧɢɹ ɡɚɜɢɫɢɬ ɨɬ ɤɨɧɰɟɧɬɪɚɰɢɢ
ɷɥɟɤɬɪɨɧɨɜ n:
16
2
2
13
r
en
E
n
Df
S
~
/
, ɬɚɤ ɱɬɨ ɩɪɢ n=0 (ɪɚɡɪɟɠɟɧ-
ɧɵɣ ɝɚɡ) r
D
of
ɢ ɷɤɪɚɧɢɪɨɜɤɚ ɢɫɱɟɡɚɟɬ. ȼɟɥɢɱɢɧɚ r
D
ɜɦɟ-
ɬɚɥɥɚɯ ~10
-8
ɫɦ (~a
B
). ɉɨɞɫɬɚɜɢɦ ɡɚɜɢɫɢɦɨɫɬɶ (8.9) ɜ ɜɵɪɚɠɟ-
ɧɢɟ ɞɥɹ ɷɧɟɪɝɢɢ (8.2)
E
err
rm
D
2
2
2
2
exp[ / ]
!
r
. (8.10)
131
ɗɤɪɚɧɢɪɨɜɚɧɢɟ ɨɫɥɚɛɥɹɟɬ ɷɧɟɪɝɢɸ ɫɜɹɡɢ, ɢ ɩɪɢ ɨɩɪɟɞɟ-
ɥɟɧɧɨɦ ɡɧɚɱɟɧɢɢ r
D
ɦɨɠɟɬ ɧɚɫɬɭɩɢɬɶ ɞɟɥɨɤɚɥɢɡɚɰɢɹ ɷɥɟɤɬɪɨ-
ɧɚ, ɢ ɩɟɪɟɯɨɞ Ɇɨɬɬɚ ɜ ɦɟɬɚɥɥɢɱɟɫɤɨɟ ɫɨɫɬɨɹɧɢɟ. ɉɨɥɭɱɢɦ ɬɨɱ-
ɤɭ ɩɟɪɟɯɨɞɚ ɢɫɯɨɞɹ ɢɡ (8.10). ɍɫɥɨɜɢɟ ɧɚ ɪɚɜɧɨɜɟɫɢɟ (8.3) ɩɪɢ-
ɜɨɞɢɬ ɤ
E
ae
r
rr
rr
B
D
2
0
2
0
0
2
{}
D
, (8.11)
ɝɞɟ r
0
~ a
B
- ɪɟɲɟɧɢɟ ɫɥɟɞɭɸɳɟɝɨ ɭɪɚɜɧɟɧɢɹ (ɭɪɚɜɧɟɧɢɹ ɪɚɜ-
ɧɨɜɟɫɢɹ
w
E/
w
r = 0)
exp[ / ]
rr
a
r
r
rr
D
BD
D
0
00
. (8.12)
ɂɡ (8.11) ɫɥɟɞɭɟɬ, ɱɬɨ ɩɪɢ r
D
< r
0
~ a
B
- ɷɧɟɪɝɢɹ ɪɚɜɧɨɜɟɫɢɹ
ɛɨɥɶɲɟ ɧɭɥɹ, ɬ.ɟ. ɧɟɬ ɫɜɹɡɚɧɧɨɝɨ ɫɨɫɬɨɹɧɢɹ, ɢ ɫɢɫɬɟɦɚ ɞɟɥɨɤɚ-
ɥɢɡɭɟɬɫɹ, ɫɬɚɧɨɜɹɫɶ ɦɟɬɚɥɥɢɱɟɫɤɨɣ. ɗɬɨ ɭɫɥɨɜɢɟ ɫ ɭɱɟɬɨɦ ɨɩ-
ɪɟɞɟɥɟɧɢɹ a
B
ɩɟɪɟɩɢɫɵɜɚɟɬɫɹ ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ:
na
B
13 13
1
43
1
4
//
()!|
S
. (8.13)
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɩɪɢ ɜɨɡɪɚɫɬɚɧɢɢ ɩɥɨɬɧɨɫɬɢ ɷɥɟɤɬɪɨɧɧɨ-
ɝɨ ɝɚɡɚ (ɬ.ɟ. ɭɜɟɥɢɱɟɧɢɢ ɞɚɜɥɟɧɢɹ ɢ ɭɦɟɧɶɲɟɧɢɢ ɦɟɠɚɬɨɦɧɨɝɨ
ɪɚɫɫɬɨɹɧɢɹ) ɞɨ ɜɟɥɢɱɢɧɵ, ɤɨɝɞɚ ɧɚ ɤɚɠɞɵɣ ɷɥɟɤɬɪɨɧ ɩɪɢɯɨ-
ɞɢɬɫɹ ɫɮɟɪɚ ɫ ɪɚɞɢɭɫɨɦ ɩɨɪɹɞɤɚ ɛɨɪɨɜɫɤɨɝɨ ɪɚɞɢɭɫɚ, ɫɢɫɬɟɦɚ
ɩɟɪɟɯɨɞɢɬ ɢɡ ɞɢɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɫɨɫɬɨɹɧɢɹ ɜ ɦɟɬɚɥɥɢɱɟɫɤɨɟ,
ɬ.ɟ. ɪɟɚɥɢɡɭɟɬɫɹ ɩɟɪɟɯɨɞ Ɇɨɬɬɚ.
Ɂɚɞɚɱɢ
8.1.
1. ɂɫɯɨɞɹ ɢɡ ɮɭɪɶɟ-ɤɨɦɩɨɧɟɧɬɵ ɩɨɬɟɧɰɢɚɥɚ
I
q
(8.8)
ɜ ɷɥɟɤɬɪɨɧɧɨɦ ɝɚɡɟ, ɪɚɫɫɱɢɬɚɬɶ ɤɨɨɪɞɢɧɚɬɧɭɸ ɡɚɜɢɫɢɦɨɫɬɶ
I
(r).
8.1.
2. Ɇɢɧɢɦɢɡɢɪɨɜɚɬɶ ɷɧɟɪɝɢɸ ɷɥɟɤɬɪɨɧɚ ɫ ɭɱɟɬɨɦ
ɷɤɪɚɧɢɪɨɜɤɢ ɜ ɩɨɥɟ ɢɨɧɚ (8.10) ɢ ɧɚɣɬɢ ɞɟɛɚɟɜɫɤɢɣ ɪɚɞɢɭɫ r
D
,
ɩɪɢ ɤɨɬɨɪɨɦ ɢɫɱɟɡɚɟɬ ɫɜɹɡɚɧɧɨɟ ɫɨɫɬɨɹɧɢɟ ɩɪɢ ɩɟɪɟɯɨɞɟ Ɇɨɬ-
ɬɚ.
132
8.2. Ɏɚɡɨɜɵɣ ɩɟɪɟɯɨɞ ɩɨɥɭɦɟɬɚɥɥ - ɢɡɨɥɹɬɨɪ
ɜ ɦɨɞɟɥɢ Ʉɟɥɞɵɲɚ-Ʉɨɩɚɟɜɚ. ɗɤɫɢɬɨɧɵ
Ɋɚɫɫɦɨɬɪɢɦ ɦɟɬɚɥɥ ɫ ɦɚɥɨɣ ɤɨɧɰɟɧɬɪɚɰɢɟɣ ɧɨɫɢɬɟɥɟɣ.
ȿɫɥɢ ɜɚɥɟɧɬɧɚɹ ɡɨɧɚ ɬɚɤɨɝɨ ɜɟɳɟɫɬɜɚ ɩɟɪɟɤɪɵɜɚɟɬɫɹ ɫ ɛɨɥɟɟ
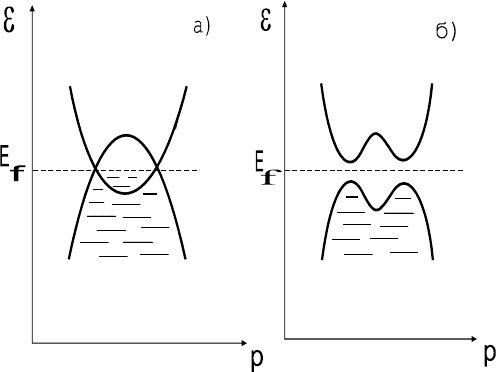
ɜɵɫɨɤɨɣ ɡɨɧɨɣ ɩɪɨɜɨɞɢɦɨɫɬɢ (ɪɢɫ.14,ɚ), ɬɨ ɫɢɫɬɟɦɚ ɜɟɞɟɬ ɫɟɛɹ
ɤɚɤ ɦɟɬɚɥɥ. ȼ ɬɚɤɨɣ ɫɢɫɬɟɦɟ ɜɨɡɦɨɠɧɵ ɤɚɤ ɷɥɟɤɬɪɨɧɧɚɹ, ɬɚɤ ɢ
ɞɵɪɨɱɧɚɹ ɩɪɨɜɨɞɢɦɨɫɬɶ, ɢ ɤɪɨɦɟ ɬɨɝɨ, ɫɜɨɛɨɞɧɵɟ ɧɨɫɢɬɟɥɢ
ɦɨɝɭɬ ɤɨɧɞɟɧɫɢɪɨɜɚɬɶɫɹ ɜ ɷɥɟɤɬɪɨɧ-ɞɵɪɨɱɧɵɟ ɩɚɪɵ - ɷɤɫɢɬɨ-
ɧɵ, ɩɪɢɜɨɞɹ ɤ
ɥɨɤɚɥɢɡɚɰɢɢ ɢ ɤ ɮɚɡɨɜɨɦɭ ɩɟɪɟɯɨɞɭ ɜ ɞɢɷɥɟɤ-
ɬɪɢɱɟɫɤɨɟ ɫɨɫɬɨɹɧɢɟ, ɱɬɨ ɨɬɪɚɠɚɟɬɫɹ ɧɚ ɡɨɧɧɨɣ ɤɚɪɬɢɧɟ
(ɪɢɫ.14,ɛ) - ɩɨɹɜɥɹɟɬɫɹ ɤɭɥɨɧɨɜɫɤɚɹ ɳɟɥɶ ɜ ɫɩɟɤɬɪɟ, ɪɚɡɞɟ-
ɥɹɸɳɚɹ ɡɨɧɵ. ɍɜɟɥɢɱɟɧɢɟ ɬɟɦɩɟɪɚɬɭɪɵ ɦɨɠɟɬ ɪɚɡɪɵɜɚɬɶ ɷɤ-
Ɋɢɫ.14. Ɂɨɧɧɚɹ ɤɚɪɬɢɧɚ ɩɨɥɭɦɟɬɚɥɥɚ ɞɥɹ ɩɟɪɟɯɨɞɚ ɦɟ-
ɬɚɥɥ - ɞɢɷɥɟɤɬɪɢɤ ɜ ɦɨɞɟɥɢ Ʉɟɥɞɵɲɚ - Ʉɨɩɚɟɜɚ:
ɚ) - ɦɟɬɚɥɥɢɱɟɫɤɨɟ ɫɨɫɬɨɹɧɢɟ, ɛ) - ɞɢɷɥɟɤɬɪɢɱɟɫɤɨɟ
ɫɨɫɬɨɹɧɢɟ (ɩɨɹɜɥɹɟɬɫɹ ɤɭɥɨɧɨɜɫɤɚɹ ɳɟɥɶ ɜ ɫɩɟɤɬɪɟ)
133

ɫɢɬɨɧɧɭɸ ɫɜɹɡɶ, ɬ.ɟ. ɩɟɪɟɯɨɞ ɦɨɠɟɬ ɩɪɨɢɫɯɨɞɢɬɶ ɩɨ ɬɟɦɩɟɪɚ-
ɬɭɪɟ.
Ɋɚɫɫɦɨɬɪɢɦ ɫɧɚɱɚɥɚ ɤɚɱɟɫɬɜɟɧɧɨ ɷɥɟɤɬɪɨɧ-ɞɵɪɨɱɧɭɸ
ɩɚɪɭ ɜ ɩɪɢɛɥɢɠɟɧɢɢ ɷɮɮɟɤɬɢɜɧɨɣ ɦɚɫɫɵ ɜɛɥɢɡɢ ɞɧɚ ɡɨɧɵ ɩɪɨ-
ɜɨɞɢɦɨɫɬɢ ɢ ɜɟɪɯɚ ɜɚɥɟɧɬɧɨɣ ɡɨɧɵ ɫ ɷɧɟɪɝɢɹɦɢ
EpmEE pmEm m
eefh f
1
2
2
2
22
22,,
h
.
ɍɱɢɬɵɜɚɹ ɜɡɚɢɦɧɨɟ ɤɭɥɨɧɨɜɫɤɨɟ ɩɪɢɬɹɠɟɧɢɟ, ɡɚɩɢɲɟɦ ɫɭɦ-
ɦɚɪɧɭɸ ɷɧɟɪɝɢɸ ɷɤɫɢɬɨɧɚ - ɷɥɟɤɬɪɨɧ-ɞɵɪɨɱɧɨɣ ɩɚɪɵ (ɡɚ ɜɵɱɟ-
ɬɨɦ ɨɬɫɱɟɬɚ ɨɬ ɭɪɨɜɧɹ Ɏɟɪɦɢ 2E
f
), ɪɚɡɞɟɥɹɹ ɢɦɩɭɥɶɫɵ ɧɚ ɢɦ-
ɩɭɥɶɫ ɨɬɧɨɫɢɬɟɥɶɧɨɝɨ ɞɜɢɠɟɧɢɹ p ɢ ɢɦɩɭɥɶɫ ɞɜɢɠɟɧɢɹ ɰɟɧɬɪɚ
ɢɧɟɪɰɢɢ ɫɢɫɬɟɦɵ P:
EE E p m p m er
pmPMer
m
mm
mm
Mm m
pmpmp mm Ppp
eh e h
eh
eh
eh
eh
ooo oo
1
2
2
22
222
21 1
2
12
22
22 ,
,,
[]/[],
o
.
(8.14)
ɉɪɟɧɟɛɪɟɝɚɹ ɞɜɢɠɟɧɢɟɦ ɰɟɧɬɪɚ ɢɧɟɪɰɢɢ (P=0), ɜɢɞɢɦ, ɱɬɨ
ɫɢɫɬɟɦɚ ɦɨɠɟɬ ɢɦɟɬɶ ɫɜɹɡɚɧɧɨɟ ɫɨɫɬɨɹɧɢɟ (ɫɦ., ɧɚɩɪɢɦɟɪ, ɚɧɚ-
ɥɢɡ (8.1)-(8.4)), ɬɚɤ ɱɬɨ ɷɧɟɪɝɢɹ ɨɬɞɟɥɶɧɨ ɷɥɟɤɬɪɨɧɚ ɢ ɞɵɪɤɢ
ɛɨɥɶɲɟ, ɱɟɦ ɫɭɦɦɚɪɧɚɹ ɷɧɟɪɝɢɹ ɩɚɪɵ.
Ɋɚɫɫɱɢɬɚɟɦ ɬɟɩɟɪɶ ɤɨɪɪɟɤɬɧɨ (ɜ ɩɨɞɯɨɞɟ Ʉɟɥɞɵɲɚ-
Ʉɨɩɚɟɜɚ) ɮɚɡɨɜɵɣ ɩɟɪɟɯɨɞ ɞɢɷɥɟɤɬɪɢɤ - ɦɟɬɚɥɥ, ɭɱɢɬɵɜɚɹ ɫɭ-
ɳɟɫɬɜɨɜɚɧɢɟ ɷɥɟɤɬɪɨɧ-ɞɵɪɨɱɧɵɯ ɩɚɪ ɜ ɫɢɫɬɟɦɟ.
Ɋɚɫɫɦɨɬɪɢɦ
ɝɚɦɢɥɶɬɨɧɢɚɧ ɩɨɥɭɦɟɬɚɥɥɚ, ɭɱɢɬɵɜɚɹ ɬɨɥɶɤɨ ɜɚ-
ɥɟɧɬɧɭɸ ɡɨɧɭ ɢ ɡɨɧɭ ɩɪɨɜɨɞɢɦɨɫɬɢ ɜɛɥɢɡɢ ɭɪɨɜɧɹ Ɏɟɪɦɢ:
HaaEpbbEp Uabba
pp pp pp ppp p
ppp
¦¦
{() ()}
''
,'
12 '
. (8.15)
Ɂɞɟɫɶ ɨɩɟɪɚɬɨɪ a
+
(b
+
) - ɨɩɟɪɚɬɨɪ ɪɨɠɞɟɧɢɹ ɷɥɟɤɬɪɨɧɚ (ɞɵɪɤɢ)
ɜ ɡɨɧɟ ɩɪɨɜɨɞɢɦɨɫɬɢ (ɜɚɥɟɧɬɧɨɣ ɡɨɧɟ), E
1
, E
2
- ɫɨɨɬɜɟɬɫɬɜɭɸ-
134

135
p
ɳɢɟ ɷɧɟɪɝɢɢ. ɉɟɪɜɵɣ ɱɥɟɧ ɜ (8.15) - ɤɢɧɟɬɢɱɟɫɤɚɹ ɷɧɟɪɝɢɹ
ɷɥɟɤɬɪɨɧɨɜ ɢ ɞɵɪɨɤ, ɜɬɨɪɨɣ - ɪɨɠɞɟɧɢɟ (ɨɩɟɪɚɬɨɪ )
ɢ ɭɧɢɱɬɨɠɟɧɢɟ (ɨɩɟɪɚɬɨɪ
P
pp
ab
P
pp
ba
p
) ɷɤɫɢɬɨɧɨɜ ɡɚ ɫɱɟɬ ɤɭɥɨ-
ɧɨɜɫɤɨɝɨ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ (ɩɪɢɬɹɠɟɧɢɹ) U
pp’
. Ⱦɥɹ ɩɪɨɫɬɨɬɵ
ɩɨɥɨɠɢɦ
mmEE pmE
eh p
{ ,
12
2
2
[
f
. ɉɟɪɟɩɢɲɟɦ ɝɚ-
ɦɢɥɶɬɨɧɢɚɧ
HaabbU
ppp pp pppp
ppp
¦¦
[P
{}
'
,'
P
'
P
p'
!
. (8.16)
ȼɬɨɪɨɟ ɫɥɚɝɚɟɦɨɟ ɢɦɟɟɬ ɜɢɞ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ
ɫɨ ɫɪɟɞɧɢɦ ɩɨɥɟɦ:
P
ppp
pp
U
¦¦
'
'
'
ppppp
p
Uba
¦
''''
'
. (8.17)
Ɉɬɫɸɞɚ, ɪɚɡɪɟɡɚɹ ɜɡɚɢɦɨɞɟɣɫɬɜɭɸɳɭɸ ɱɚɫɬɶ ɝɚɦɢɥɶɬɨɧɢɚɧɚ
ɩɨ ɫɪɟɞɧɟɦɭ ɩɨɥɸ
abba ab ba ab ba
pppp pp pp pp pp
| ! !
'' '' ''
,
ɢɦɟɟɦ
Haabbabba
ppp pp ppp ppp
pp
¦¦
[
{}{
*
' }'
. (8.18)
Ɇɨɞɟɥɶ (8.18) ɦɨɠɧɨ ɞɢɚɝɨɧɚɥɢɡɨɜɚɬɶ, ɟɫɥɢ ɜɜɟɫɬɢ ɤɚ-
ɧɨɧɢɱɟɫɤɢɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɨɩɟɪɚɬɨɪɨɜ
au v bu v
au v bu v
pppppppppp
pppppppppp
DE ED
DE ED
,,
,,
(8.19)
ɩɪɢ ɷɬɨɦ ɧɨɜɵɟ ɨɩɟɪɚɬɨɪɵ ɬɚɤɠɟ ɮɟɪɦɢɨɧɵ:
DD DD G
qq q q qq'' '
, ɟɫɥɢ u
p
2
+v
p
2
=1.

ɉɨɞɫɬɚɜɢɜ (8.19) ɜ (8.18), ɩɨɥɭɱɚɟɦ, ɢɫɩɨɥɶɡɭɹ ɫɨɨɬɧɨɲɟɧɢɹ
ɤɨɦɦɭɬɚɰɢɢ:
Huv
uv uv
pp pp p p p ppp
p
pp pp p p p ppp
p
¦
¦
{ }{[ ] }
{ }{[ ] }.
DD EE [
DE ED [
22
22
2
2
'
'
uv
1
(8.20)
Ɂɚɧɭɥɹɹ ɤɨɷɮɮɢɰɢɟɧɬ ɩɪɢ ɧɟɞɢɚɝɨɧɚɥɶɧɨɦ ɫɥɚɝɚɟɦɨɦ
(
D
+
E
+
,
DE
), ɩɨɥɭɱɚɟɦ ɭɪɚɜɧɟɧɢɹ ɞɥɹ ɨɩɪɟɞɟɥɟɧɢɹ u,v:
[] ,uv uv uv
ppp ppp pp
22 22
20 '
[
. (8.21)
Ɋɟɲɚɹ (8.21), ɧɚɯɨɞɢɦ
vu
p
p
p
p
p
p
pp
22
1
2
1
1
2
1 (), (),
p
22
[
H
[
H
H[
' . (8.22)
Ƚɚɦɢɥɶɬɨɧɢɚɧ (8.20) ɩɪɟɞɫɬɚɜɥɹɟɬɫɹ ɩɪɢ ɷɬɨɦ ɜ ɞɢɚɝɨɧɚɥɶɧɨɦ
ɜɢɞɟ
H
ppp pp
p
¦
HDD EE
{ }. (8.23)
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɜɟɥɢɱɢɧɚ
H
p
ɢɦɟɟɬ ɫɦɵɫɥ ɫɩɟɤɬɪɚ ɜɨɡɛɭɠɞɟɧɢɣ
ɧɚɞ ɩɨɜɟɪɯɧɨɫɬɶɸ Ɏɟɪɦɢ ɢ ɝɨɜɨɪɢɬ ɨ ɩɨɹɜɥɟɧɢɢ ɤɨɧɟɱɧɨɣ
ɤɭɥɨɧɨɜɫɤɨɣ ɳɟɥɢ (~2' ɧɚ ɭɪɨɜɧɟ Ɏɟɪɦɢ ɦɟɠɞɭ ɜɚɥɟɧɬɧɨɣ
ɡɨɧɨɣ ɢ ɡɨɧɨɣ ɩɪɨɜɨɞɢɦɨɫɬɢ (ɪɢɫ.14,ɛ).
ȼɜɟɞɟɦ ɮɭɧɤɰɢɢ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɜɨɡɛɭɠɞɟɧɢɣ ɜ ɡɨɧɚɯ:
nn
pppppp
DE
DD EE
! !
,
.
p
p
)
(8.24)
ɉɭɫɬɶ m
e
=m
h
®,ɩɪɢ ɷɬɨɦ ɪɚɫɩɪɟɞɟɥɟɧɢɟ ɷɥɟɤ-
ɬɪɨɧɨɜ:
nnn
pp
DE
faau v unvn
pppppppppppp
! ! !
2222
1
DD EE
(
. (8.25)
136
ȼ (8.25) ɭɱɬɟɧɨ, ɱɬɨ ɜɤɥɚɞ ɧɟɞɢɚɝɨɧɚɥɶɧɵɯ ɱɥɟɧɨɜ ɪɚɜɟɧ ɧɭɥɸ:
! !
DE ED
pp pp
0.
Ɏɭɧɤɰɢɹ ɪɚɫɩɪɟɞɟɥɟɧɢɹ n
p
ɮɟɪɦɢɟɜɫɤɚɹ ɫ ɧɭɥɟɜɵɦ ɯɢɦɩɨɬɟɧ-
ɰɢɚɥɨɦ
P
, ɬɚɤ ɤɚɤ ɱɢɫɥɨ ɤɜɚɡɢɱɚɫɬɢɰ ɧɟ ɫɨɯɪɚɧɹɟɬɫɹ :
n
T
p
p
1
1exp[ ]
.
H
(8.26)
Ɉɩɪɟɞɟɥɢɦ ɭɪɚɜɧɟɧɢɟ ɞɥɹ ɩɚɪɚɦɟɬɪɚ ɩɨɪɹɞɤɚ
(
ɢ ɳɟɥɢ ɜ ɫɩɟɤ
-
ɬɪɟ
) '
Ⱦɥɹ ɷɬɨɝɨ ɩɨɞɫɬɚɜɢɦ ɜ ɨɩɪɟɞɟɥɟɧɢɟ
(8.17)
ɫɨɨɬɧɨɲɟ
-
ɧɢɹ
(8.19), (8.22)
ɢ
(8.24).
ɉɨɫɥɟ ɧɟɤɨɬɨɪɵɯ ɩɪɟɨɛɪɚɡɨɜɚɧɢɣ
ɢɦɟɟɦ
'
'
'
pppppp
p
pp
p
pp
p
p
Uuv n
Un
¦
¦
''' '
'
'
'
''
'
'
()
()
12
2
12
22
[
.
(8.27)
ȼ (8.27) ɭɱɬɟɧɨ, ɱɬɨ ɢɡ (8.21)-(8.22) ɫɥɟɞɭɟɬ
uv
pp
p
pp
'
'
2
22
[
.
ɉɭɫɬɶ ɜɡɚɢɦɨɞɟɣɫɬɜɢɟ U
pp’
ɦɟɧɶɲɟ ɧɭɥɹ ɜ ɧɟɤɨɬɨɪɨɦ
ɞɢɚɩɚɡɨɧɟ |
[
p
-
[
p’
|<
Z
ɝɞɟ ɨɫɭɳɟɫɬɜɥɹɟɬɫɹ ɷɥɟɤɬɪɨɧ-ɞɵɪɨɱɧɨɟ
ɩɪɢɬɹɠɟɧɢɟ). ȿɫɥɢ ɩɨɥɨɠɢɬɶ U
pp’
= - V ɜ ɞɢɚɩɚɡɨɧɟ (-
Z
,
Z
) ɢ
ɪɚɜɧɵɦ ɧɭɥɸ ɜɧɟ ɷɬɨɝɨ ɞɢɚɩɚɡɨɧɚ ɩɨ ɷɧɟɪɝɢɢ, ɬɨ ɢɡ (8.27) ɩɨ-
ɥɭɱɚɟɦ, ɭɱɢɬɵɜɚɹ, ɱɬɨ ' ɜ ɷɬɨɦ ɫɥɭɱɚɟ ɧɟ ɡɚɜɢɫɢɬ ɨɬ p:
''
'
'
³
VN
T
dth
[[
[
[
Z
Z
() [ ]
22
22
2
1
2
. (8.28)
137
ɍɪɚɜɧɟɧɢɟ (8.28) ɫɨɜɩɚɞɚɟɬ ɫ ɭɪɚɜɧɟɧɢɟɦ ȻɄɒ ɞɥɹ ɫɜɟɪɯɩɪɨ-
ɜɨɞɧɢɤɨɜ. Ɂɞɟɫɶ
NEE
ff
() ()/ ~
[U[ [
| 2 const
- ɨɞ-
ɧɨɫɩɢɧɨɜɚɹ ɩɥɨɬɧɨɫɬɶ ɫɨɫɬɨɹɧɢɣ, ɜɛɥɢɡɢ ɭɪɨɜɧɹ Ɏɟɪɦɢ ɫɥɚɛɨ
ɡɚɜɢɫɹɳɚɹ ɨɬ ɷɧɟɪɝɢɢ. Ɉɩɪɟɞɟɥɢɜ ɤɚɤ ɤɨɧɫɬɚɧɬɭ ɫɜɹɡɢ ɜɟɥɢɱɢ-
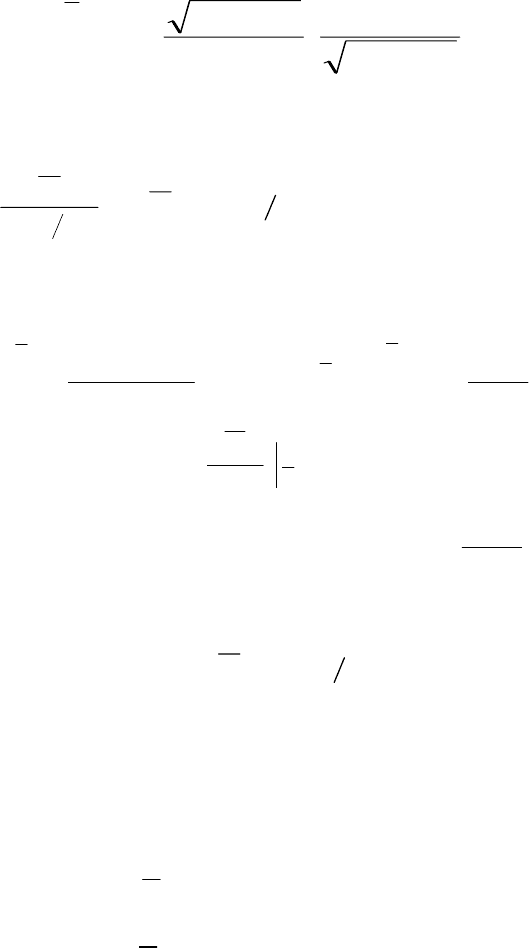
ɧɭ
O
NV()0,ɨɤɨɧɱɚɬɟɥɶɧɨ ɩɨɥɭɱɚɟɦ ɢɧɬɟɝɪɚɥɶɧɨɟ ɭɪɚɜɧɟ-
ɧɢɟ ɧɚ ':
1
2
1
22
0
22
³
O[
[
[
Z
dth[ ]
'
'
T
. (8.29)
ɉɪɨɚɧɚɥɢɡɢɪɭɟɦ (8.29). ɉɪɢ ɧɭɥɟɜɨɣ ɬɟɦɩɟɪɚɬɭɪɟ ɢɧɬɟɝɪɚɥ
ɛɟɪɟɬɫɹ ɬɨɱɧɨ, ɢ ɦɵ ɩɨɥɭɱɚɟɦ ɩɚɪɚɦɟɬɪ ɩɨɪɹɞɤɚ
' |
Z
O
ZOO
sh( )
exp[ ], ,
1
21 1T 0
. (8.30)
ȼ ɩɪɟɞɟɥɟ
'o
0 ɧɚɣɞɟɦ ɤɪɢɬɢɱɟɫɤɭɸ ɬɟɦɩɟɪɚɬɭɪɭ. ȼ ɷɬɨɦ
ɫɥɭɱɚɟ
1
2
2
0577 4
0
0
2
2
0
2
21
2
0
³³
³
!!
f
O[
[
[
ZJ
S
JS
Z
Z
Z
Z
d
th
th d
ch
d
ch
(/ )
ln |
ln
ln{ } ,
exp[ ], . ln[ / ]
ln
.
/
/
/
T
xx x
x
x
T
CC x
x
x
c
T
T
c
T
c
c
c
(8.31)
ɂɡ (8.31) ɫɥɟɞɭɟɬ ɫɨɨɬɧɨɲɟɧɢɟ ɧɚ ɤɪɢɬɢɱɟɫɤɭɸ ɬɟɦɩɟɪɚɬɭɪɭ:
T
c
|114 1.exp[
Z
]
O
. (8.32)
Ɉɛɳɢɣ ɜɢɞ ɬɟɦɩɟɪɚɬɭɪɧɨɣ ɡɚɜɢɫɢɦɨɫɬɢ 'ɩɨɤɚɡɚɧ ɧɚ ɪɢɫ.1,ɛ.
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɦɵ ɩɨɥɭɱɢɥɢ ɤɨɧɟɱɧɭɸ ɬɟɦɩɟɪɚɬɭɪɭ,
ɜɵɲɟ ɤɨɬɨɪɨɣ ɤɭɥɨɧɨɜɫɤɚɹ ɳɟɥɶ ɜ ɫɩɟɤɬɪɟ ɫɯɥɨɩɵɜɚɟɬɫɹ, ɢ
ɩɪɨɢɫɯɨɞɢɬ ɩɟɪɟɯɨɞ ɢɡ ɞɢɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɜ ɦɟɬɚɥɥɢɱɟɫɤɨɟ ɫɨ-
ɫɬɨɹɧɢɟ. Ɇɚɫɲɬɚɛ ɤɪɢɬɢɱɟɫɤɨɣ ɬɟɦɩɟɪɚɬɭɪɵ ɨɩɪɟɞɟɥɹɟɬɫɹ
ɱɚɫɬɨɬɨɣ ɨɛɪɟɡɚɧɢɹ
Z
ɢ ɤɨɧɫɬɚɧɬɨɣ ɫɜɹɡɢ
O
, ɧɨ ɜ ɥɸɛɨɦ ɫɥɭ-
ɱɚɟ ɨɧ ɫɭɳɟɫɬɜɟɧɧɨ ɛɨɥɶɲɟ ɱɟɦ ɜ ɫɜɟɪɯɩɪɨɜɨɞɧɢɤɚɯ. ȿɫɥɢ
ɱɚɫɬɨɬɚ ɨɛɪɟɡɚɧɢɹ
Z
~ 1 ɷȼ (ɩɨɪɹɞɨɤ ɤɭɥɨɧɨɜɫɤɢɯ ɷɧɟɪɝɢɣ),
138

ɬɨ ɢɡ-ɡɚ ɩɟɪɟɧɨɪɦɢɪɨɜɤɢ ɡɚ ɫɱɟɬ ɤɨɧɫɬɚɧɬɵ ɫɜɹɡɢ ɤɪɢɬɢɱɟɫɤɚɹ
ɬɟɦɩɟɪɚɬɭɪɚ ɦɨɠɟɬ ɛɵɬɶ ɩɨɪɹɞɤɚ ɧɟɫɤɨɥɶɤɢɯ ɫɨɬɟɧ ɤɟɥɶɜɢɧ:
T
c
~ 100 - 500 K .
Ɂɚɞɚɱɢ
8.2.
1. ɉɪɟɨɛɪɚɡɨɜɚɬɶ ɝɚɦɢɥɶɬɨɧɢɚɧ ɦɨɞɟɥɢ Ʉɟɥɞɵɲɚ-
Ʉɨɩɚɟɜɚ (8.16) ɜ ɫɩɢɧɨɜɵɣ ɝɚɦɢɥɶɬɨɧɢɚɧ ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫɨ
ɫɩɢɧɨɜɨɣ ɚɧɚɥɨɝɢɟɣ ɞɥɹ ɫɜɟɪɯɩɪɨɜɨɞɧɢɤɨɜ (ɫɦ. ɝɥɚɜɭ 4), ɩɨ-
ɫɬɚɜɢɜ ɜ ɫɨɨɬɜɟɬɫɬɜɢɟ ɨɩɟɪɚɬɨɪɵ ɞɵɪɨɤ ɢ ɷɥɟɤɬɪɨɧɨɜ ɦɚɬɪɢ-
ɰɚɦ ɉɚɭɥɢ:
Iaa bb
ba i
ab i
pp pp
Z
pp
XY
pp
XY
V
PV
PV
,
()
()
1
2
1
2
V
V
,
.
ɉɨɥɭɱɢɬɶ ɜ ɩɪɢɛɥɢɠɟɧɢɢ ɫɪɟɞɧɟɝɨ ɩɨɥɹ ɭɪɚɜɧɟɧɢɟ ɧɚ ɩɚɪɚ-
ɦɟɬɪ ɩɨɪɹɞɤɚ.
8.2.
2. Ⱦɨɤɚɡɚɬɶ, ɱɬɨ ɤɜɚɡɢɱɚɫɬɢɰɵ
DE
, ɜɜɨɞɢɦɵɟ ɫɨɨɬ-
ɧɨɲɟɧɢɟɦ (8.19), ɹɜɥɹɸɬɫɹ ɮɟɪɦɢɨɧɚɦɢ.
8.2.
3. ɂɫɯɨɞɹ ɢɡ ɭɪɚɜɧɟɧɢɹ ɞɥɹ ɩɚɪɚɦɟɬɪɚ ɩɨɪɹɞɤɚ (8.29)
ɪɚɫɫɱɢɬɚɬɶ
'
ɩɪɢ ɧɭɥɟɜɨɣ ɬɟɦɩɟɪɚɬɭɪɟ ɢ ɩɟɪɜɭɸ ɷɤɫɩɨɧɟɧɰɢ-
ɚɥɶɧɭɸ ɩɨɩɪɚɜɤɭ ɤ ɧɟɦɭ ~exp(-
'
/T).
8.2.
4. Ɋɚɫɫɱɢɬɚɬɶ ɩɚɪɚɦɟɬɪ ɩɨɪɹɞɤɚ
'
(T) ɜɛɥɢɡɢ ɤɪɢɬɢ-
ɱɟɫɤɨɣ ɬɟɦɩɟɪɚɬɭɪɵ ɢ ɩɨɤɚɡɚɬɶ ɪɚɫɯɨɞɢɦɨɫɬɶ ɩɪɨɢɡɜɨɞɧɨɣ
d
'
/dT|
Tc
.
139
