Елесин В.Ф., Кашурников В.А. Физика фазовых переходов
Подождите немного. Документ загружается.

8.3.1.8. ɉɨɤɚɡɚɬɶ, ɱɬɨ ɜɜɟɞɟɧɧɵɟ ɫɨɨɬɧɨɲɟɧɢɹɦɢ (8.53)
ɨɩɟɪɚɬɨɪɵ ɹɜɥɹɸɬɫɹ ɫɩɢɧɨɜɵɦɢ ɨɩɟɪɚɬɨɪɚɦɢ S=1/2.
8.3.1.
9. ȼɵɪɚɡɢɬɶ ɤɨɦɦɭɬɚɬɨɪ (8.52) ɱɟɪɟɡ ɫɩɢ-
ɧɨɜɵɟ ɨɩɟɪɚɬɨɪɵ, ɬ.ɟ. ɩɨɥɭɱɢɬɶ ɫɨɨɬɧɨɲɟɧɢɟ (8.54).
iST
mix
[, ]
8.3.2. ɉɟɪɟɯɨɞ ɦɟɬɚɥɥ - ɞɢɷɥɟɤɬɪɢɤ
ɜ ɦɨɞɟɥɢ ɏɚɛɛɚɪɞɚ
150
U
20
Ɋɚɫɫɦɨɬɪɢɦ ɫɧɚɱɚɥɚ ɩɪɟɞɟɥ ɫɢɥɶɧɨɝɨ ɤɭɥɨɧɨɜɫɤɨɝɨ
ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ U >>t. ɉɭɫɬɶ ɢɦɟɟɬɫɹ ɩɨɥɨɜɢɧɧɨɟ ɡɚɩɨɥɧɟɧɢɟ
N=N
a
. ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɷɥɟɤɬɪɨɧɵ ɡɚɩɟɪɬɵ ɫɢɥɶɧɵɦ ɤɭɥɨɧɨɦ
ɤɚɠɞɵɣ ɧɚ ɫɜɨɟɦ ɭɡɥɟ. Ɍɨɝɞɚ ɜ ɝɚɦɢɥɶɬɨɧɢɚɧɟ ɏɚɛɛɚɪɞɚ (8.37)
ɦɨɠɧɨ ɩɪɟɧɟɛɪɟɱɶ ɩɟɪɟɫɤɨɤɨɜɵɦ ɱɥɟɧɨɦ. Ƚɚɦɢɥɶɬɨɧɢɚɧ ɞɢɚ-
ɝɨɧɚɥɟɧ, ɢ ɷɧɟɪɝɢɹ ɪɚɜɧɚ
EEnnUnnNENE
i
i
i
i
i
n
p
n
p
¦
{( ) } ( )
010
2 , (8.57)
ɝɞɟ N
1
- ɱɢɫɥɨ ɭɡɥɨɜ ɫ ɨɞɧɢɦ ɷɥɟɤɬɪɨɧɨɦ; N
2
- c ɞɜɭɦɹ. ȼ (8.41)
ɦɵ ɧɟɹɜɧɨ ɞɨɛɚɜɢɥɢ ɨɬɫɱɟɬ ɷɧɟɪɝɢɢ ɨɬ E
0
(ɱɬɨ ɷɤɜɢɜɚɥɟɧɬɧɨ
ɞɨɛɚɜɤɟ ɤ ɝɚɦɢɥɶɬɨɧɢɚɧɭ (8.37) ɱɥɟɧɚ
).Ea a
ii
i
0
VV
V
¦
E
0
- ɷɧɟɪɝɢɹ, ɧɟɨɛɯɨɞɢɦɚɹ, ɱɬɨɛɵ ɫɜɹɡɚɬɶ ɷɥɟɤɬɪɨɧ ɜ
ɢɡɨɥɢɪɨɜɚɧɧɨɦ ɚɬɨɦɟ. U +E
0
- ɷɧɟɪɝɢɹ, ɧɟɨɛɯɨɞɢɦɚɹ ɞɥɹ ɩɪɢ-
ɫɨɟɞɢɧɟɧɢɹ ɜɬɨɪɨɝɨ ɷɥɟɤɬɪɨɧɚ ɫ ɩɪɨɬɢɜɨɩɨɥɨɠɧɨ ɧɚɩɪɚɜɥɟɧ-
ɧɵɦ ɫɩɢɧɨɦ. Ɂɨɧɧɚɹ ɤɚɪɬɢɧɚ ɬɚɤɨɣ ɫɢɫɬɟɦɵ ɫɨɫɬɨɢɬ ɢɡ ɞɜɭɯ
ɡɨɧ ɫ ɷɧɟɪɝɢɣ E
0
ɢ U +E
0
. ȼ ɨɫɧɨɜɧɨɦ ɫɨɫɬɨɹɧɢɢ N ɢɦɟɸɳɢɯɫɹ
ɷɥɟɤɬɪɨɧɨɜ ɨɛɥɚɞɚɸɬ ɷɧɟɪɝɢɟɣ E
0
, ɢ ɜ ɤɚɠɞɨɦ ɚɬɨɦɟ ɪɚɡɦɟɳɟ-
ɧɨ ɩɨ ɨɞɧɨɦɭ ɷɥɟɤɬɪɨɧɭ (N
1
=N, N
2
=0). ȼ ɷɬɨɦ ɩɪɟɞɟɥɶɧɨɦ ɫɥɭ-
ɱɚɟ ɢɦɟɟɬ ɦɟɫɬɨ ɫɬɪɨɝɚɹ ɥɨɤɚɥɢɡɚɰɢɹ ɷɥɟɤɬɪɨɧɨɜ.
ȿɫɥɢ ɦɵ ɧɚɱɢɧɚɟɦ “ɜɤɥɸɱɚɬɶ” ɩɟɪɟɫɤɨɤ t, ɬɨ ɷɬɢ ɥɨɤɚ-
ɥɢɡɨɜɚɧɧɵɟ ɫɨɫɬɨɹɧɢɹ ɧɚɱɢɧɚɸɬ ɪɚɫɳɟɩɥɹɬɶɫɹ ɜ ɡɨɧɵ ɲɢɪɢ-
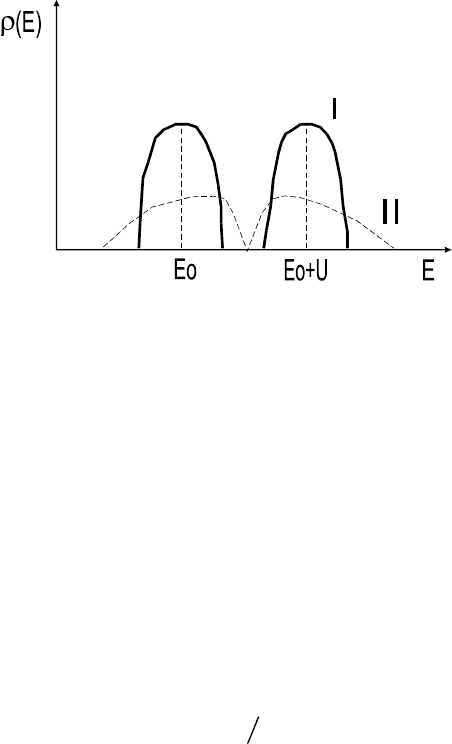
ɧɨɣ ɩɨɪɹɞɤɚ 2Zt, ɝɞɟ Z - ɱɢɫɥɨ ɛɥɢɠɚɣɲɢɯ ɫɨɫɟɞɟɣ (ɷɬɨ ɬɚɤ
ɧɚɡɵɜɚɟɦɵɟ ɧɢɠɧɹɹ ɢ ɜɟɪɯɧɹɹ ɏɚɛɛɚɪɞɨɜɫɤɢɟ ɡɨɧɵ, ɪɢɫ.15).
151
ɉɨɤɚ ɡɨɧɵ ɧɟ ɫɥɢɥɢɫɶ, ɜɟɳɟɫɬɜɨ ɨɫɬɚɟɬɫɹ
ɞɢɷɥɟɤɬɪɢɤɨɦ. ɉɪɢ ɤɪɢɬɢɱɟɫɤɨɣ ɜɟɥɢɱɢɧɟ ɪɚɫɳɟɩɥɟɧɢɹ (ɤɪɢ-
ɬɢɱɟɫɤɨɦ ɡɧɚɱɟɧɢɢ ɩɚɪɚɦɟɬɪɚ t/U ~ Z), ɨɩɪɟɞɟɥɹɟɦɨɝɨ ɩɨɫɬɨ-
ɹɧɧɨɣ ɪɟɲɟɬɤɢ (ɱɟɪɟɡ t) ɢ ɤɭɥɨɧɨɜɫɤɢɦ ɭɡɟɥɶɧɵɦ ɜɡɚɢɦɨɞɟɣ-
ɫɬɜɢɟɦ, ɳɟɥɶ ɢɫɱɟɡɚɟɬ. ȼ ɬɚɤɨɦ ɫɥɭɱɚɟ ɢɦɟɟɬ ɦɟɫɬɨ ɩɟɪɟɯɨɞ ɨɬ
ɥɨɤɚɥɢɡɨɜɚɧɧɨɝɨ ɨɩɢɫɚɧɢɹ ɤ ɡɨɧɧɨɣ ɦɨɞɟɥɢ, ɬ.ɟ. ɨɬ ɞɢɷɥɟɤɬɪɢ-
ɤɚ ɤ ɦɟɬɚɥɥɭ.
Ɋɢɫ.15. Ɋɚɫɳɟɩɥɟɧɢɟ
ɡɨɧɵ ɡɚ ɫɱɟɬ ɤɭɥɨ-
ɧɨɜɫɤɨɝɨ ɜɡɚɢɦɨɞɟɣ-
ɫɬɜɢɹ ɜ ɦɨɞɟɥɢ ɏɚɛ-
ɛɚɪɞɚ:
(t/U)
II
>(t/U)
I
ɂɬɚɤ, ɜ ɦɨɞɟɥɢ ɏɚɛɛɚɪɞɚ ɜɨɡɦɨɠɟɧ ɮɚɡɨɜɵɣ ɩɟɪɟɯɨɞ
ɦɟɬɚɥɥ - ɞɢɷɥɟɤɬɪɢɤ ɜ ɡɚɜɢɫɢɦɨɫɬɢ ɨɬ ɫɨɨɬɧɨɲɟɧɢɹ ɚɦɩɥɢɬɭɞɵ
ɩɟɪɟɫɤɨɤɚ t ɢ ɤɭɥɨɧɨɜɫɤɨɝɨ ɨɬɬɚɥɤɢɜɚɧɢɹ U.
Ⱥɦɩɥɢɬɭɞɚ ɩɟɪɟɫɤɨɤɚ ɱɭɜɫɬɜɢɬɟɥɶɧɚ ɤ ɩɨɫɬɨɹɧɧɨɣ ɪɟɲɟɬɤɢ a,
ɬɚɤ ɤɚɤ ɢɡ ɫɨɨɬɧɨɲɟɧɢɹ (8.34) ɜ ɩɪɢɛɥɢɠɟɧɢɢ ɛɥɢɠɚɣɲɢɯ ɫɨ-
ɫɟɞɟɣ:
ta
B
~exp( )a , ɩɨɷɬɨɦɭ ɩɟɪɟɯɨɞ ɦɨɠɟɬ ɩɪɨɢɫɯɨ-
ɞɢɬɶ, ɧɚɩɪɢɦɟɪ, ɩɪɢ ɢɡɦɟɧɟɧɢɢ ɜɧɟɲɧɟɝɨ ɩɪɢɥɨɠɟɧɧɨɝɨ ɞɚɜ-
ɥɟɧɢɹ, ɢɥɢ ɢɡ-ɡɚ ɫɬɪɭɤɬɭɪɧɨɣ ɩɟɪɟɫɬɪɨɣɤɢ ɫ ɢɡɦɟɧɟɧɢɟɦ ɩɨ-
ɫɬɨɹɧɧɨɣ ɪɟɲɟɬɤɢ, ɢɥɢ ɢɡ-ɡɚ ɬɟɦɩɟɪɚɬɭɪɧɨɝɨ ɪɚɫɲɢɪɟɧɢɹ.
ɋɥɟɞɭɟɬ ɨɬɦɟɬɢɬɶ, ɱɬɨ ɜ ɨɞɧɨɦɟɪɧɨɣ ɫɢɬɭɚɰɢɢ ɩɨɥɭɱɟɧɨ
ɬɨɱɧɨɟ ɪɟɲɟɧɢɟ ɦɨɞɟɥɢ ɏɚɛɛɚɪɞɚ (Ʌɢɛ, ȼɭ, 1964). Ɉɫɧɨɜɧɨɣ
ɜɵɜɨɞ - ɨɬɫɭɬɫɬɜɢɟ ɩɟɪɟɯɨɞɚ ɦɟɬɚɥɥ - ɞɢɷɥɟɤɬɪɢɤ ɩɪɢ ɥɸɛɨɦ
ɩɚɪɚɦɟɬɪɟ
U/t >0 (ɫɦ. ɧɢɠɟ).

ȼɜɟɞɟɧɢɟ ɤ ɡɚɞɚɱɚɦ 8.3.2.1-8.3.2.2. (ɨɬɫɭɬɫɬɜɢɟ ɮɚɡɨ-
ɜɨɝɨ ɩɟɪɟɯɨɞɚ ɦɟɬɚɥɥ - ɞɢɷɥɟɤɬɪɢɤ ɜ ɨɞɧɨɦɟɪɧɨɣ ɦɨɞɟɥɢ
ɏɚɛɛɚɪɞɚ; ɬɨɱɧɨɟ ɪɟɲɟɧɢɟ Ʌɢɛɚ ɢ ȼɭ).
ȼ 1968ɝ. Ʌɢɛɨɦ ɢ ȼɭ
(Lieb, Wu) ɛɵɥɨ ɩɪɨɞɟɦɨɧɫɬɪɢɪɨɜɚɧɨ ɬɨɱɧɨɟ ɪɟɲɟɧɢɟ ɨɞɧɨ-
ɦɟɪɧɨɣ ɦɨɞɟɥɢ ɏɚɛɛɚɪɞɚ. Ɉɧɢ ɢɫɫɥɟɞɨɜɚɥɢ ɦɨɞɟɥɶ ɦɟɬɨɞɨɦ
ɚɧɡɚɬɰɚ Ȼɟɬɟ, ɨɫɧɨɜɵɜɚɹɫɶ ɧɚ ɪɚɧɟɟ ɪɟɲɟɧɧɨɣ əɧɝɨɦ ɩɪɨɛɥɟɦɟ
ɨɞɧɨɦɟɪɧɨɣ ɫɢɫɬɟɦɵ ɦɧɨɝɢɯ ɱɚɫɬɢɰ ɫ ɞɟɥɶɬɚɮɭɧɤɰɢɨɧɧɵɦ
ɨɬɬɚɥɤɢɜɚɧɢɟɦ ɢ ɧɚ ɤɜɚɧɬɨɜɨɦ ɦɟɬɨɞɟ ɨɛɪɚɬɧɨɣ ɡɚɞɚɱɢ ɪɚɫ-
ɫɟɹɧɢɹ (ɄɆɈɁ). Ȼɵɥɨ ɩɨɤɚɡɚɧɨ, ɱɬɨ ɨɞɧɨɦɟɪɧɚɹ ɫɢɫɬɟɦɚ, ɨɩɢ-
ɫɵɜɚɟɦɚɹ ɝɚɦɢɥɶɬɨɧɢɚɧɨɦ ɏɚɛɛɚɪɞɚ,
ɧɟ ɩɟɪɟɯɨɞɢɬ ɜ ɦɟɬɚɥɥɢ-
ɱɟɫɤɨɟ ɫɨɫɬɨɹɧɢɟ ɧɢ ɩɪɢ ɤɚɤɨɦ ɡɧɚɱɟɧɢɢ ɩɚɪɚɦɟɬɪɚ t/U, ɬ.ɟ.
ɜɫɟɝɞɚ ɹɜɥɹɟɬɫɹ ɞɢɷɥɟɤɬɪɢɤɨɦ.
Ƚɚɦɢɥɶɬɨɧɢɚɧ ɨɞɧɨɦɟɪɧɨɣ ɩɟɪɢɨɞɢɱɟɫɤɨɣ ɏɚɛɛɚɪɞɨɜ-
ɫɤɨɣ ɰɟɩɨɱɤɢ ɫ ɜɡɚɢɦɨɞɟɣɫɬɜɢɟɦ ɬɨɥɶɤɨ ɫ ɛɥɢɠɚɣɲɢɦɢ ɫɨɫɟ-
ɞɹɦɢ ɢɦɟɟɬ ɜɢɞ:
H t aa aa Unn
ii ii
i
i
i
i
n
p
¦¦
()
,
VV VV
V
11
. (8.58)
ɍɱɢɬɵɜɚɹ ɫɨɨɬɧɨɲɟɧɢɹ (8.39), ɞɨɫɬɚɬɨɱɧɨ ɪɚɫɫɦɨɬɪɟɬɶ
ɦɟɧɟɟ ɱɟɦ ɧɚɩɨɥɨɜɢɧɭ ɡɚɩɨɥɧɟɧɧɭɸ ɡɨɧɭ. Ɇɵ ɧɟ ɛɭɞɟɦ ɩɨɞ-
ɪɨɛɧɨ ɨɩɢɫɵɜɚɬɶ ɝɪɨɦɨɡɞɤɢɟ ɜɵɱɢɫɥɟɧɢɹ Ʌɢɛɚ ɢ ȼɭ, ɢ ɢɫɫɥɟ-
ɞɭɟɦ ɨɤɨɧɱɚɬɟɥɶɧɵɣ ɪɟɡɭɥɶɬɚɬ (ɞɨɫɬɚɬɨɱɧɨ ɩɨɞɪɨɛɧɨ ɪɟɲɟɧɢɟ
Ʌɢɛɚ ɢ ȼɭ ɢɡɥɨɠɟɧɨ ɜ ɤɧɢɝɟ [6]). Ɉɤɨɧɱɚɬɟɥɶɧɵɣ ɨɬɜɟɬ Ʌɢɛɚ ɢ
ȼɭ ɜ ɢɧɬɟɝɪɚɥɶɧɨɦ ɜɢɞɟ ɢɦɟɬ ɜɢɞ:
21
8
16
2
8
16
2
4
4
22
22
22
SU OV O
O
U
O
SV O
OV O
OO
() ()
(sin)
;
()
(sin)
()
'(')
(')
.
pd
U
Up
dp p
U
Up
d
U
U
B
B
Q
Q
B
B
³
³
³
(8.59)
(U=U/t). ȼɯɨɞɹɳɢɟ ɜ ɩɨɥɭɱɟɧɧɵɟ ɭɪɚɜɧɟɧɢɹ ɜɟɥɢɱɢɧɵ Q ɢ B
ɨɩɪɟɞɟɥɹɸɬɫɹ ɧɨɪɦɢɪɨɜɤɨɣ ɧɚ ɱɢɫɥɨ ɫɩɢɧɨɜ ɜɜɟɪɯ M ɢ ɩɨɥɧɨɟ
ɱɢɫɥɨ ɷɥɟɤɬɪɨɧɨɜ N:
152
153
N
p
dMNdppN
B
B
a
Q
Q
a
OV O U
() / , () /
³³
. (8.60)
ȼ ɬɚɤɨɦ ɤɨɧɬɢɧɭɚɥɶɧɨɦ ɩɪɟɞɫɬɚɜɥɟɧɢɢ ɷɧɟɪɝɢɹ ɨɫɧɨɜɧɨɝɨ ɫɨ-
ɫɬɨɹɧɢɹ ɫɢɫɬɟɦɵ
ENdpp
a
Q
Q
0
2
³
U
( ) cos . (8.61)
ȿɫɬɟɫɬɜɟɧɧɨ, ɷɧɟɪɝɢɹ ɫɢɫɬɟɦɵ ɛɭɞɟɬ ɡɚɜɢɫɟɬɶ ɨɬ M ɢ N ɱɟɪɟɡ
ɩɚɪɚɦɟɬɪ Q ɫɭɱɟɬɨɦ (8.60), ɬɚɤ ɱɬɨ
E
0
= E
0
(M, M’,U), M’ = N - M.
Ʌɢɛ ɢ Ɇɚɬɬɢɫ ɞɨɤɚɡɚɥɢ, ɱɬɨ ɨɫɧɨɜɧɨɟ ɫɨɫɬɨɹɧɢɟ ɮɟɪɦɢ-
ɨɧɧɨɣ ɫɢɫɬɟɦɵ - ɫɢɧɝɥɟɬɧɨɟ. ɗɬɨ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɜɫɟ ɱɢɫɥɚ
O
ɡɚɩɨɥɧɹɸɬ ɜɟɫɶ ɢɧɬɟɪɜɚɥ (-f,+f, ɬ.ɟ. ɜɫɸɞɭ ɜ ɢɧɬɟɝɪɚɥɚɯ
ɧɚɞɨ ɩɨɥɨɠɢɬɶ B =
f
, ɚ ɢɫɯɨɞɹ ɢɡ ɫɨɨɬɧɨɲɟɧɢɹ (8.60) ɞɥɹ
O
ɢ p
ɫɥɟɞɭɟɬ ɬɚɤɠɟ, ɱɬɨ Q =
S
. Ɍɨɝɞɚ ɭɪɚɜɧɟɧɢɹ (8.59) ɦɨɠɧɨ ɪɟ-
ɲɢɬɶ ɦɟɬɨɞɨɦ Ɏɭɪɶɟ ɢ ɩɨɥɭɱɢɬɶ
VO
S
Z
O
Z
ZZ
Z
U
SS
ZZ
Z
Z
()
cos( ) ( )
exp( ) exp( )
,
() cos
cos( sin ) ( )
exp( )
.
f
f
³
³
1
44
1
2
1
12
0
0
0
0
J
UU
d
pp
pJ
U
d
(8.62)
Ⱦɥɹ ɫɢɧɝɥɟɬɧɨɝɨ ɨɫɧɨɜɧɨɝɨ ɫɨɫɬɨɹɧɢɹ (M=M’=N
a
/2) ɷɧɟɪɝɢɸ
ɦɨɠɧɨ ɪɚɫɫɱɢɬɚɬɶ ɢɡ (8.61):
EN NU N
JJ
U
d
aa a0
01
0
1
2
1
2
4
12
(,,)
() ()
[exp( )]
f
³
Z
Z
ZZ
Z
. (8.63)
ȼ ɮɨɪɦɭɥɚɯ (8.62)-(8.63) J
0
ɢ J
1
- ɮɭɧɤɰɢɢ Ȼɟɫɫɟɥɹ ɧɭɥɟɜɨɝɨ ɢ
ɩɟɪɜɨɝɨ ɩɨɪɹɞɤɚ.
ɂɫɫɥɟɞɭɟɦ ɬɟɩɟɪɶ ɫ ɩɨɦɨɳɶɸ ɩɨɥɭɱɟɧɧɵɯ ɬɨɱɧɵɯ ɪɟ-
ɡɭɥɶɬɚɬɨɜ, ɹɜɥɹɟɬɫɹ ɥɢ ɨɫɧɨɜɧɨɟ ɫɨɫɬɨɹɧɢɟ ɩɪɨɜɨɞɹɳɢɦ ɢɥɢ

ɞɢɷɥɟɤɬɪɢɱɟɫɤɢɦ. Ⱦɥɹ ɷɬɨɝɨ ɧɟɨɛɯɨɞɢɦɨ ɜɵɱɢɫɥɢɬɶ ɫɥɟɞɭɸ-
ɳɢɟ ɯɢɦɢɱɟɫɤɢɟ ɩɨɬɟɧɰɢɚɥɵ (M=N
a
/2):
P
P
EM MU EMMU
EMMU EM MU
00
00
1
1
( , ,) (, ,),
( , ,) ( , ,).
(8.64)
ȼ ɨɞɧɨɱɚɫɬɢɱɧɨɦ ɫɩɟɤɬɪɟ ɜɟɥɢɱɢɧɚ
P
+
-
P
-
ɹɜɥɹɟɬɫɹ ɳɟɥɶɸ
ɦɟɠɞɭ ɜɟɪɯɧɟɣ ɢ ɧɢɠɧɟɣ ɯɚɛɛɚɪɞɨɜɫɤɢɦɢ ɩɨɞɡɨɧɚɦɢ (ɫɦ.
ɪɢɫ.15). ɉɨɷɬɨɦɭ ɩɪɢ ɩɨɥɨɜɢɧɧɨɦ ɡɚɩɨɥɧɟɧɢɢ (ɡɚɩɨɥɧɟɧɚ
ɧɢɠɧɹɹ ɩɨɞɡɨɧɚ), ɟɫɥɢ
P
+
>
P
-
, ɬɨ ɫɨɫɬɨɹɧɢɟ ɞɢɷɥɟɤɬɪɢɱɟɫɤɨɟ,
ɜ ɩɪɨɬɢɜɧɨɦ ɫɥɭɱɚɟ - ɦɟɬɚɥɥɢɱɟɫɤɨɟ. ɂɡ ɪɟɡɭɥɶɬɚɬɨɜ (8.62)-
(8.63) ɦɨɠɧɨ ɩɨɥɭɱɢɬɶ:
P
P
P
Z
ZZ
Z
f
f
³
¦
U
J
U
d
nU nU
n
n
,
()
[exp( )]
()[( ) ].
/
24
12
411
1
4
1
2
1
0
2212
1
(8.65)
ɂɡ (8.65) ɜ ɩɪɟɞɟɥɶɧɵɯ ɫɥɭɱɚɹɯ ɩɨɥɭɱɚɟɦ:
PP
S
S
f
of !!
o o
®
°
°
¯
°
°
¦
U
U
U
UUn
n
U
n
4
16
21
4
2
421
21
00
3
0
ln , ;
exp{ / [ ]}
()
,.
(8.66)
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ,
P
+
>
P
-
, ɬ.ɟ. ɨɞɧɨɦɟɪɧɚɹ ɦɨɞɟɥɶ ɏɚɛ-
ɛɚɪɞɚ ɜɫɟɝɞɚ ɧɚɯɨɞɢɬɫɹ ɜ ɫɨɫɬɨɹɧɢɢ ɢɡɨɥɹɬɨɪɚ. ɗɬɨ ɫɨɫɬɨɹɧɢɟ,
ɤɨɝɞɚ ɢɦɟɸɬɫɹ ɞɜɟ ɩɨɞɡɨɧɵ, ɪɚɫɳɟɩɥɟɧɧɵɟ ɤɭɥɨɧɨɜɫɤɢɦ
ɜɡɚɢɦɨɞɟɣɫɬɜɢɟɦ U ɢ ɫ ɡɚɩɨɥɧɟɧɧɨɣ ɧɢɠɧɟɣ ɩɨɞɡɨɧɨɣ, ɧɚɡɵ-
ɜɚɸɬ “ɯɚɛɛɚɪɞɨɜɫɤɢɣ ɞɢɷɥɟɤɬɪɢɤ”.
Ɂɚɞɚɱɢ
8.3.2.
1. Ɋɟɲɢɬɶ ɢɧɬɟɝɪɚɥɶɧɵɟ ɭɪɚɜɧɟɧɢɹ Ʌɢɛɚ ɢ ȼɭ ɦɟ-
ɬɨɞɨɦ Ɏɭɪɶɟ ɞɥɹ ɩɥɨɬɧɨɫɬɟɣ ɪɚɫɩɪɟɞɟɥɟɧɢɹ
U
(p) ɢ
V
(
O
) ɜɨɫ-
ɧɨɜɧɨɦ ɫɨɫɬɨɹɧɢɢ ɨɞɧɨɦɟɪɧɨɣ ɦɨɞɟɥɢ ɏɚɛɛɚɪɞɚ.
154

155
8.3.2.2. ɉɨɥɭɱɢɬɶ ɚɫɢɦɬɨɬɢɱɟɫɤɢɟ ɫɨɨɬɧɨɲɟɧɢɹ ɞɥɹ
ɪɚɡɧɨɫɬɢ ɯɢɦɢɱɟɫɤɢɯ ɩɨɬɟɧɰɢɚɥɨɜ
P
+
-
P
-
ɜ ɩɪɟɞɟɥɟ U
o
0 ɢ
U
of
ɞɥɹ ɨɞɧɨɦɟɪɧɨɣ ɦɨɞɟɥɢ ɏɚɛɛɚɪɞɚ ɢɫɯɨɞɹ ɢɡ ɬɨɱɧɨɝɨ
ɫɨɨɬɧɨɲɟɧɢɹ (8.65).
ɍɤɚɡɚɧɢɟ
: ɜ ɨɞɧɨɦ ɩɪɟɞɟɥɶɧɨɦ ɫɥɭɱɚɟ ɛɪɚɬɶ ɢɧɬɟɝɪɚɥɶ-
ɧɵɣ ɜɚɪɢɚɧɬ (8.65), ɜ ɞɪɭɝɨɦ - ɜɵɪɚɠɟɧɢɟ (8.65) ɜ ɜɢɞɟ ɫɭɦɦɵ.
8.4. Ɏɚɡɨɜɵɣ ɩɟɪɟɯɨɞ ɦɟɬɚɥɥ - ɢɡɨɥɹɬɨɪ
ɞɥɹ ɧɟɭɩɨɪɹɞɨɱɟɧɧɨɣ ɫɢɫɬɟɦɵ.
Ɇɨɞɟɥɶ Ⱥɧɞɟɪɫɨɧɚ. Ʌɨɤɚɥɢɡɚɰɢɹ
Ʌɨɤɚɥɢɡɨɜɚɬɶ ɧɨɫɢɬɟɥɢ ɦɨɠɧɨ ɧɟ ɬɨɥɶɤɨ ɩɟɪɟɫɬɪɨɣɤɨɣ
ɫɩɟɤɬɪɚ ɡɚ ɫɱɟɬ ɤɭɥɨɧɨɜɫɤɨɝɨ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ ɢ ɢɡɦɟɧɟɧɢɹ
ɩɨɫɬɨɹɧɧɨɣ ɪɟɲɟɬɤɢ, ɧɨ ɢ ɫ ɩɨɦɨɳɶɸ ɜɜɟɞɟɧɢɹ ɩɪɢɦɟɫɟɣ. ɉɨ-
ɤɚɠɟɦ ɷɬɨ ɧɚ ɩɪɢɦɟɪɟ ɦɨɞɟɥɢ Ⱥɧɞɟɪɫɨɧɚ.
ɇɚɱɧɟɦ ɨɛɫɭɠɞɟɧɢɟ ɫ ɩɨɧɹɬɢɹ ɞɥɢɧɵ ɥɨɤɚɥɢɡɚɰɢɢ ɷɥɟɤ-
ɬɪɨɧɚ ɜ ɤɪɢɫɬɚɥɥɟ ɩɪɢ ɧɚɥɢɱɢɢ ɧɟɭɩɨɪɹɞɨɱɟɧɧɨɝɨ ɩɨɬɟɧɰɢɚɥɚ
ɩɪɢɦɟɫɟɣ. ȿɫɥɢ ɤɪɢɫɬɚɥɥ ɢɞɟɚɥɟɧ, ɬɨ ɩɪɨɜɨɞɢɦɨɫɬɶ ɢ ɩɨɞɜɢɠ-
ɧɨɫɬɶ ɷɥɟɤɬɪɨɧɚ ɛɭɞɭɬ ɛɟɫɤɨɧɟɱɧɵɦɢ, ɬ.ɟ. ɧɨɫɢɬɟɥɢ ɦɨɝɭɬ
ɞɢɮɮɭɧɞɢɪɨɜɚɬɶ ɩɨ ɪɟɲɟɬɤɟ ɛɟɡ ɪɚɫɫɟɹɧɢɹ ɞɨ ɛɟɫɤɨɧɟɱɧɨɫɬɢ.
ɇɚɪɭɲɟɧɢɹ ɢɞɟɚɥɶɧɨɣ ɪɟɲɟɬɤɢ (ɬ.ɟ. ɮɨɧɨɧɵ, ɬɨɱɟɱɧɵɟ ɞɟɮɟɤ-
ɬɵ ɢ ɩɪɢɦɟɫɢ) ɨɝɪɚɧɢɱɢɜɚɸɬ ɫɪɟɞɧɸɸ ɞɥɢɧɭ ɫɜɨɛɨɞɧɨɝɨ ɩɪɨ-
ɛɟɝɚ ɷɥɟɤɬɪɨɧɚ, ɬ.ɤ. ɨɧ ɧɚɱɢɧɚɟɬ ɨɬɪɚɠɚɬɶɫɹ ɢ ɪɚɫɫɟɢɜɚɬɶɫɹ ɨɬ
ɞɟɮɟɤɬɨɜ ɪɟɲɟɬɤɢ ɢ ɫɛɢɜɚɬɶ ɮɚɡɭ ɫɜɨɟɣ ɜɨɥɧɨɜɨɣ ɮɭɧɤɰɢɢ.
ɂɧɚɱɟ
ɝɨɜɨɪɹ, ɜ ɪɟɡɭɥɶɬɚɬɟ ɜɨɡɦɭɳɟɧɢɹ ɮɚɡɨɜɚɹ ɤɨɝɟɪɟɧɬɧɨɫɬɶ
ɜɨɥɧɨɜɨɣ ɮɭɧɤɰɢɢ ɨɝɪɚɧɢɱɟɧɚ ɤɨɧɟɱɧɨɣ ɞɥɢɧɨɣ ɤɨɝɟɪɟɧɬɧɨ-
ɫɬɢ. ɉɨ ɦɟɪɟ ɜɨɡɪɚɫɬɚɧɢɹ ɫɬɟɩɟɧɢ ɪɚɡɭɩɨɪɹɞɨɱɟɧɢɹ ɞɥɢɧɚ
ɫɜɨɛɨɞɧɨɝɨ ɩɪɨɛɟɝɚ ɢ ɞɥɢɧɚ ɤɨɝɟɪɟɧɬɧɨɫɬɢ ɭɦɟɧɶɲɚɸɬɫɹ. ɇɟ-
ɫɦɨɬɪɹ ɧɚ ɷɬɨ, ɫɨɫɬɨɹɧɢɟ ɨɫɬɚɟɬɫɹ ɜɫɟ ɟɳɟ ɧɟɥɨɤɚɥɢɡɨɜɚɧɧɵɦ.
ɇɨ ɞɚɥɶɧɟɣɲɢɣ ɪɨɫɬ ɧɟɭɩɨɪɹɞɨɱɟɧɧɨɫɬɢ ɦɨɠɟɬ ɩɪɢɜɟɫɬɢ ɤ
ɥɨɤɚɥɢɡɨɜɚɧɧɵɦ ɫɨɫɬɨɹɧɢɹɦ, ɬ.ɟ. ɤ ɫɨɫɬɨɹɧɢɹɦ, ɨɝɪɚɧɢɱɟɧɧɵɦ

ɤɨɧɟɱɧɵɦɢ ɨɛɥɚɫɬɹɦɢ. ɂɯ ɩɪɨɬɹɠɟɧɧɨɫɬɶ ɦɨɠɟɬ ɛɵɬɶ ɨɩɢɫɚɧɚ
ɤɨɥɢɱɟɫɬɜɟɧɧɨ ɨɩɪɟɞɟɥɟɧɧɨɣ ɞɥɢɧɨɣ ɥɨɤɚɥɢɡɚɰɢɢ.
Ɉɛɫɭɞɢɦ ɷɬɨ ɜ ɪɚɦɤɚɯ ɦɨɞɟɥɢ Ⱥɧɞɟɪɫɨɧɚ. Ɉɧ ɪɚɫɫɦɚɬ-
ɪɢɜɚɥ ɬɪɟɯɦɟɪɧɭɸ ɬɨɱɟɱɧɭɸ ɪɟɲɟɬɤɭ, ɡɚɩɨɥɧɟɧɧɭɸ ɭɡɥɚɦɢ ɫ
ɷɧɟɪɝɢɟɣ E
n
. ɉɪɢ ɧɚɥɢɱɢɢ ɩɟɪɟɫɤɨɤɨɜ ɫ ɚɦɩɥɢɬɭɞɨɣ t
nm
ɢɪɚ-
ɜɟɧɫɬɜɟ ɭɡɟɥɶɧɵɯ ɷɧɟɪɝɢɣ ɜɨɡɧɢɤɚɟɬ ɷɧɟɪɝɟɬɢɱɟɫɤɚɹ ɡɨɧɚ ɫ
ɲɢɪɢɧɨɣ B ~ 2Zt, ɝɞɟ Z - ɱɢɫɥɨ ɛɥɢɠɚɣɲɢɯ ɫɨɫɟɞɟɣ; t - ɚɦɩɥɢ-
ɬɭɞɚ ɩɟɪɟɫɤɨɤɚ ɧɚ ɫɨɫɟɞɧɢɣ ɭɡɟɥ. Ɍɚɤɭɸ ɦɨɞɟɥɶ ɦɵ ɭɠɟ ɪɚɫ-
ɫɦɚɬɪɢɜɚɥɢ ɜ ɩɪɢɛɥɢɠɟɧɢɢ ɫɢɥɶɧɨɣ ɫɜɹɡɢ (ɫɦ. ɜɵɪɚɠɟɧɢɟ
(6.1)) ɫ ɪɚɜɧɵɦɢ ɷɧɟɪɝɢɹɦɢ ɧɚ ɭɡɥɚɯ E
n
=E
0
=const. Ⱦɥɹ ɪɚɫ-
ɫɦɨɬɪɟɧɢɹ ɪɚɡɭɩɨɪɹɞɨɱɟɧɢɹ Ⱥɧɞɟɪɫɨɧ ɜɜɨɞɢɬ ɫɬɚɬɢɫɬɢɱɟɫɤɢɣ
ɪɚɡɛɪɨɫ ɷɧɟɪɝɢɣ E
n
ɩɨ ɨɛɥɚɫɬɢ ɫ ɲɢɪɢɧɨɣ W, ɤɨɬɨɪɚɹ ɹɜɥɹɟɬɫɹ
ɫɬɟɩɟɧɶɸ ɪɚɡɭɩɨɪɹɞɨɱɟɧɢɹ ɫɢɫɬɟɦɵ (ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɨɣ ɤɨɧ-
ɰɟɧɬɪɚɰɢɢ ɩɪɢɦɟɫɟɣ), ɬ.ɟ. E
n
ɪɚɫɩɪɟɞɟɥɟɧɵ ɫɥɭɱɚɣɧɵɦ ɨɛɪɚ-
ɡɨɦ ɪɚɜɧɨɦɟɪɧɨ ɩɨ ɢɧɬɟɪɜɚɥɭ (-W/2,W/2). Ɍɨɝɞɚ ɝɚɦɢɥɶɬɨɧɢɚɧ
Ⱥɧɞɟɪɫɨɧɚ ɜ ɭɡɟɥɶɧɨɦ ɩɪɟɞɫɬɚɜɥɟɧɢɢ ɢɦɟɟɬ ɜɢɞ:
HEaa ta
nn n
n
nm n m
ij
z
¦¦
a . (8.67)
Ɂɞɟɫɶ ɞɥɹ ɩɪɨɫɬɨɬɵ ɪɚɫɫɦɚɬɪɢɜɚɸɬɫɹ ɛɟɫɫɩɢɧɨɜɵɟ ɱɚɫɬɢɰɵ, ɢ
ɭɱɢɬɵɜɚɟɬɫɹ ɜɡɚɢɦɨɞɟɣɫɬɜɢɟ ɬɨɥɶɤɨ ɫ ɛɥɢɠɚɣɲɢɦɢ ɫɨɫɟɞɹɦɢ
(t
nm
= t). Ɋɚɫɫɦɨɬɪɢɦ ɜɟɪɨɹɬɧɨɫɬɶ P ɜɨɡɜɪɚɳɟɧɢɹ ɷɥɟɤɬɪɨɧɚ ɜ
ɧɟɤɨɬɨɪɵɣ ɭɡɟɥ i ɱɟɪɟɡ ɛɟɫɤɨɧɟɱɧɨɟ ɜɪɟɦɹ, ɟɫɥɢ ɫɧɚɱɚɥɚ ɨɧ
ɧɚɯɨɞɢɥɫɹ ɧɚ ɷɬɨɦ ɭɡɥɟ. ȿɫɥɢ ɷɥɟɤɬɪɨɧ ɛɵɥ ɢɫɯɨɞɧɨ ɥɨɤɚɥɢɡɨ-
ɜɚɧ, ɬɨ ɟɝɨ ɞɢɮɮɭɡɢɹ ɩɨ ɤɪɢɫɬɚɥɥɭ ɨɝɪɚɧɢɱɟɧɚ ɤɨɧɟɱɧɵɦ ɨɛɴ-
ɟɦɨɦ, ɢ P
z
0. ɉɪɢ ɩɨɥɧɨɣ ɞɟɥɨɤɚɥɢɡɚɰɢɢ ɷɥɟɤɬɪɨɧ ɧɟ ɜɟɪɧɟɬ-
ɫɹ, ɢ P= 0 . Ⱥɧɞɟɪɫɨɧ ɫɦɨɝ ɩɨɤɚɡɚɬɶ, ɱɬɨ ɩɚɪɚɦɟɬɪɨɦ, ɜɟɥɢɱɢɧɚ
ɤɨɬɨɪɨɝɨ ɨɩɪɟɞɟɥɹɟɬ ɩɟɪɟɯɨɞ ɦɟɠɞɭ ɷɬɢɦɢ ɞɜɭɦɹ ɚɥɶɬɟɪɧɚɬɢ-
ɜɚɦɢ, ɹɜɥɹɟɬɫɹ ɨɬɧɨɲɟɧɢɟ ɫɬɟɩɟɧɢ ɪɚɡɭɩɨɪɹɞɨɱɟɧɢɹ ɤ ɲɢɪɢɧɟ
ɡɨɧɵ: W/B (ɨɰɟɧɤɢ Ⱥɧɞɟɪɫɨɧɚ ɞɚɸɬ, ɱɬɨ ɩɪɢ W/B>(W/B)
c
,
(W/B)
c
~5 ɫɨɫɬɨɹɧɢɟ ɷɥɟɤɬɪɨɧɚ ɜ ɰɟɧɬɪɟ ɡɨɧɵ ɫɬɚɧɨɜɢɬɫɹ ɥɨɤɚ-
ɥɢɡɨɜɚɧɧɵɦ).
156
Ʉɚɱɟɫɬɜɟɧɧɨ ɩɨɥɭɱɟɧɧɵɣ ɪɟɡɭɥɶɬɚɬ ɦɨɠɧɨ ɨɛɴɹɫɧɢɬɶ
ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ. ɂɡɜɟɫɬɧɨ, ɱɬɨ ɨɬɞɟɥɶɧɵɣ ɞɟɮɟɤɬ ɤɪɢ-
ɫɬɚɥɥɢɱɟɫɤɨɣ ɪɟɲɟɬɤɢ ɩɪɢɜɨɞɢɬ ɤ ɨɬɳɟɩɥɟɧɢɸ (ɢ ɥɨɤɚɥɢɡɚ-
ɰɢɢ) ɫɨɫɬɨɹɧɢɹ ɨɬ ɤɪɚɹ ɡɨɧɵ ɩɪɨɜɨɞɢɦɨɫɬɢ. ɋ ɪɨɫɬɨɦ ɱɢɫɥɚ
ɞɟɮɟɤɬɨɜ ɱɢɫɥɨ ɥɨɤɚɥɢɡɨɜɚɧɧɵɯ
ɫɨɫɬɨɹɧɢɣ ɜɧɟ ɡɨɧɵ ɨɛɴɟɞɢɧɹɟɬɫɹ ɜ ɡɨɧɭ (ɩɪɢɦɟɫɧɚɹ ɡɨɧɚ),
ɤɨɬɨɪɚɹ ɦɨɠɟɬ ɩɟɪɟɤɪɵɜɚɬɶɫɹ ɫ ɡɨɧɨɣ ɞɟɥɨɤɚɥɢɡɨɜɚɧɧɵɯ ɫɨ-
ɫɬɨɹɧɢɣ (ɡɨɧɨɣ ɩɪɨɜɨɞɢɦɨɫɬɢ). ȼ ɫɥɭɱɚɟ ɚɧɞɟɪɫɨɧɨɜɫɤɨɝɨ ɪɚ-
ɡɭɩɨɪɹɞɨɱɟɧɢɹ ɧɚɛɥɸɞɚɸɬɫɹ ɚɧɚɥɨɝɢɱɧɵɟ ɹɜɥɟɧɢɹ, ɬ.ɟ. ɩɪɢ
ɭɜɟɥɢɱɟɧɢɢ ɫɬɟɩɟɧɢ ɪɚɡɭɩɨɪɹɞɨɱɟɧɢɹ ɫɨɫɬɨɹɧɢɹ ɭ ɤɪɚɟɜ ɷɧɟɪ-
ɝɟɬɢɱɟɫɤɨɣ ɡɨɧɵ ɩɟɪɜɵɦɢ ɫɬɚɧɨɜɹɬɫɹ ɥɨɤɚɥɢɡɨɜɚɧɧɵɦɢ ɢ ɨɞ-
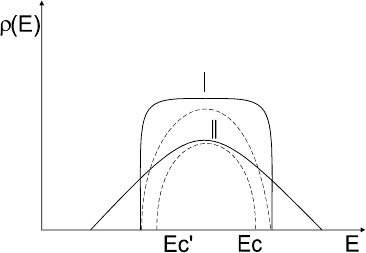
ɧɨɜɪɟɦɟɧɧɨ ɫɞɜɢɝɚɸɬɫɹ ɜ ɷɧɟɪɝɟɬɢɱɟɫɤɭɸ ɳɟɥɶ (ɪɢɫ. 16). Ɂɨɧɚ
ɩɪɢɨɛɪɟɬɚɟɬ ɯɜɨɫɬɵ ɫ ɥɨɤɚɥɢɡɨɜɚɧɧɵɦɢ ɫɨɫɬɨɹɧɢɹɦɢ ɭ ɜɟɪɯ-
ɧɟɝɨ ɢ ɧɢɠɧɟɝɨ ɤɪɚɟɜ. ɋ ɪɨɫɬɨɦ ɧɟɭɩɨɪɹɞɨɱɟɧɧɨɫɬɢ ɝɪɚɧɢɰɵ
E
c
ɢ E
c’
(ɬɨɱɤɢ ɪɚɡɞɟɥɟɧɢɹ ɥɨɤɚɥɢɡɨɜɚɧɧɵɯ ɢ ɞɟɥɨɤɚɥɢɡɨɜɚɧ-
ɧɵɯ ɫɨɫɬɨɹɧɢɣ) ɩɪɢɛɥɢɠɚɸɬɫɹ
Ɋɢɫ. 16. ɉɥɨɬɧɨɫɬɶ ɫɨɫɬɨɹ-
ɧɢɣ (ɫɩɥɨɲɧɵɟ ɥɢɧɢɢ) ɜ
ɦɨɞɟɥɢ Ⱥɧɞɟɪɫɨɧɚ; ɩɭɧɤ-
ɬɢɪɨɦ ɜɧɭɬɪɢ ɡɨɧ ɨɝɪɚɧɢ-
ɱɟɧɚ ɨɛɥɚɫɬɶ ɞɟɥɨɤɚɥɢɡɨ-
ɜɚɧɧɵɯ ɫɨɫɬɨɹɧɢɣ; E
c
, E
c’
-
ɝɪɚɧɢɰɚ ɦɟɠɞɭ ɥɨɤɚɥɢɡɨ-
ɜɚɧɧɵɦɢ ɢ ɞɟɥɨɤɚɥɢɡɨɜɚɧ-
ɧɵɦɢ ɫɨɫɬɨɹɧɢɹɦɢ
ɞɪɭɝ ɤ ɞɪɭɝɭ ɢ ɜɫɬɪɟɱɚɸɬɫɹ ɜ ɰɟɧɬɪɟ ɡɨɧɵ. ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɡɨɧɭ
ɡɚɩɨɥɧɹɸɬ ɬɨɥɶɤɨ ɥɨɤɚɥɢɡɨɜɚɧɧɵɟ ɫɨɫɬɨɹɧɢɹ. ɗɬɨ ɩɪɨɢɫɯɨɞɢɬ
ɢɦɟɧɧɨ ɩɪɢ W/B ~ (W/B)
c
.
Ɇɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ ɭɫɥɨɜɢɟ ɥɨɤɚɥɢɡɚɰɢɢ Ⱥɧɞɟɪɫɨɧɚ
ɬɚɤɠɟ ɢɡ ɫɥɟɞɭɸɳɢɯ ɫɨɨɛɪɚɠɟɧɢɣ. ɉɭɫɬɶ ɜ ɦɨɞɟɥɢ ɫɢɥɶɧɨɣ
ɫɜɹɡɢ ɡɨɧɚ (ɫ ɲɢɪɢɧɨɣ B ~ 2Zt, ɫɦ.ɪɢɫ.10) ɩɨɱɬɢ ɡɚɩɨɥɧɟɧɚ, ɬ.ɟ.
157
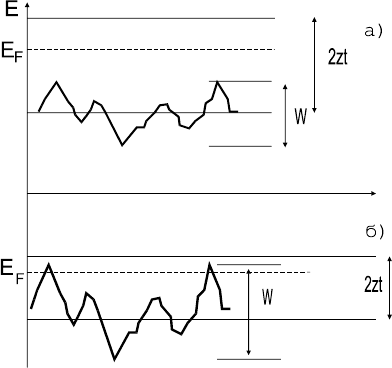
Ɋɢɫ. 17. ɉɟɪɟɯɨɞ
ɦɟɬɚɥɥ - ɢɡɨɥɹɬɨɪ ɜ
ɦɨɞɟɥɢ Ⱥɧɞɟɪɫɨɧɚ:
ɚ - W < E
f
;
ɛ - W > E
f
158
E
f
~ B. Ɍɨɝɞɚ ɭɫɥɨɜɢɟ W >
B ɩɟɪɟɯɨɞɢɬ ɜ W > E
f
, ɬ.ɟ. ɩɪɢ ɫɬɟɩɟɧɢ ɛɟɫɩɨɪɹɞɤɚ ɛɨɥɶɲɟ
ɷɧɟɪɝɢɢ Ɏɟɪɦɢ ɧɚɫɬɭɩɚɟɬ ɞɟɥɨɤɚɥɢɡɚɰɢɹ. ɗɬɨ ɦɨɠɧɨ ɨɛɴɹɫ-
ɧɢɬɶ ɬɟɦ, ɱɬɨ ɷɥɟɤɬɪɨɧɵ ɩɪɨɜɨɞɢɦɨɫɬɢ, ɢɦɟɸɳɢɟ ɤɢɧɟɬɢɱɟ-
ɫɤɭɸ ɷɧɟɪɝɢɸ ~ E
f
, ɧɟ ɱɭɜɫɬɜɭɸɬ ɛɟɫɩɨɪɹɞɨɤ, ɩɨɤɚ ɜɟɥɢɱɢɧɚ
ɫɥɭɱɚɣɧɨɝɨ ɩɨɬɟɧɰɢɚɥɚ ɦɟɧɶɲɟ ɢɯ ɤɢɧɟɬɢɱɟɫɤɨɣ ɷɧɟɪɝɢɢ, ɢ
ɨɧɢ ɦɨɝɭɬ ɫɜɨɛɨɞɧɨ ɞɜɢɝɚɬɶɫɹ ɧɚɞ ɫɥɭɱɚɣɧɵɦɢ ɩɨɬɟɧɰɢɚɥɶ-
ɧɵɦɢ ɛɚɪɶɟɪɚɦɢ (ɪɢɫ.17). Ʉɚɤ ɬɨɥɶɤɨ ɜɟɥɢɱɢɧɚ ɫɬɟɩɟɧɢ ɪɚɡɭ-
ɩɨɪɹɞɨɱɟɧɢɹ W (ɦɚɤɫɢɦɚɥɶɧɚɹ ɜɟɥɢɱɢɧɚ ɫɥɭɱɚɣɧɨɝɨ ɩɨɬɟɧ-
ɰɢɚɥɚ, ɪɢɫ. 17) ɞɨɫɬɢɝɚɟɬ E
f
, ɩɨɹɜɥɹɟɬɫɹ ɫɢɥɶɧɨɟ ɪɚɫɫɟɹɧɢɟ
ɷɥɟɤɬɪɨɧɚ ɧɚ ɷɬɨɦ ɩɨɬɟɧɰɢɚɥɟ ɢ ɤɨɧɟɱɧɚɹ ɞɥɢɧɚ ɥɨɤɚɥɢɡɚɰɢɢ.
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɩɟɪɟɯɨɞ ɦɟɬɚɥɥ - ɢɡɨɥɹɬɨɪ ɜ ɧɟɭɩɨɪɹ-
ɞɨɱɟɧɧɨɦ ɜɟɳɟɫɬɜɟ ɩɨ ɦɨɞɟɥɢ Ⱥɧɞɟɪɫɨɧɚ ɩɪɨɢɫɯɨɞɢɬ ɢɡ-ɡɚ
ɥɨɤɚɥɢɡɚɰɢɢ ɷɥɟɤɬɪɨɧɨɜ (ɚɧɞɟɪɫɨɧɨɜɫɤɨɣ ɥɨɤɚɥɢɡɚɰɢɢ) ɩɪɢ
ɜɨɡɪɚɫɬɚɧɢɢ ɪɚɡɭɩɨɪɹɞɨɱɟɧɢɹ ɫɢɫɬɟɦɵ (ɤɨɧɰɟɧɬɪɚɰɢɢ ɩɪɢɦɟ-
ɫɟɣ) ɞɨ ɬɟɯ ɩɨɪ, ɩɨɤɚ ɚɦɩɥɢɬɭɞɚ ɪɚɡɭɩɨɪɹɞɨɱɟɧɢɹ W ɧɟ ɫɬɚɧɨ-
ɜɢɬɫɹ ɛɨɥɶɲɟ ɷɧɟɪɝɢɢ Ɏɟɪɦɢ: W > E
f
.
____________
159
9. ɄɈɇȾȿɇɋȺɐɂə ɂ ɋȼȿɊɏɌȿɄɍɑȿɋɌɖ
ȼ ȻɈɁȿ-ȽȺɁȿ
Ɋɚɫɫɦɨɬɪɢɦ ɬɟɩɟɪɶ ɮɚɡɨɜɵɟ ɩɟɪɟɯɨɞɵ, ɩɪɨɢɫɯɨɞɹɳɢɟ ɜ
ɫɢɫɬɟɦɚɯ ɫ ɢɫɯɨɞɧɨ ɛɨɡɨɧɧɵɦɢ ɫɬɟɩɟɧɹɦɢ ɫɜɨɛɨɞɵ. Ⱦɨ ɫɢɯ
ɩɨɪ ɦɵ ɢɦɟɥɢ ɞɟɥɨ ɫ ɛɨɡɟ-ɫɬɚɬɢɫɬɢɤɨɣ ɩɪɢ ɢɫɫɥɟɞɨɜɚɧɢɢ ɬɟɪ-
ɦɨɞɢɧɚɦɢɤɢ ɫɩɢɧɨɜɵɯ ɜɨɡɛɭɠɞɟɧɢɣ - ɦɚɝɧɨɧɨɜ. ɂɫɫɥɟɞɭɟɦ ɜ
ɷɬɨɣ ɝɥɚɜɟ ɫɬɚɬɢɫɬɢɱɟɫɤɢɟ ɫɜɨɣɫɬɜɚ ɢɞɟɚɥɶɧɨɝɨ ɢ ɫɥɚɛɨ ɧɟɢɞɟ-
ɚɥɶɧɨɝɨ ɛɨɡɟ-ɝɚɡɚ, ɛɨɡɟ-ɤɨɧɞɟɧɫɚɰɢɸ ɩɪɢ ɧɢɡɤɢɯ ɬɟɦɩɟɪɚɬɭ-
ɪɚɯ, ɤɪɢɬɟɪɢɣ ɫɜɟɪɯɬɟɤɭɱɟɫɬɢ Ʌɚɧɞɚɭ. Ɉɬɦɟɬɢɦ, ɱɬɨ ɢɡ ɪɟɚɥɶ-
ɧɵɯ ɫɢɫɬɟɦ ɫ ɛɨɡɟ-ɫɬɚɬɢɫɬɢɤɨɣ ɦɨɠɧɨ ɜɵɞɟɥɢɬɶ ɮɨɧɨɧɵ (ɤɨ-
ɥɟɛɚɧɢɹ ɤɪɢɫɬɚɥɥɢɱɟɫɤɨɣ ɪɟɲɟɬɤɢ) ɜ ɬɜɟɪɞɨɦ ɬɟɥɟ, ɫɜɟɪɯɬɟɤɭ-
ɱɢɣ ɝɟɥɢɣ, ɮɨɬɨɧɵ, ɤɭɩɟɪɨɜɫɤɢɟ ɩɚɪɵ ɜ ɫɜɟɪɯɩɪɨɜɨɞɧɢɤɚɯ,
ɛɨɡɟ-ɤɨɧɞɟɧɫɚɰɢɸ ɷɤɫɢɬɨɧɧɵɯ ɜɨɡɛɭɠɞɟɧɢɣ ɜ ɩɨɥɭɩɪɨɜɨɞɧɢ-
ɤɚɯ, ɫɩɢɧɨɜɵɟ ɜɨɡɛɭɠɞɟɧɢɹ ɜ ɦɚɝɧɟɬɢɤɚɯ ɢ ɬ.ɞ.
9.1. Ȼɨɡɟ-ɤɨɧɞɟɧɫɚɰɢɹ ɜ ɢɞɟɚɥɶɧɨɦ ɝɚɡɟ -
ɮɚɡɨɜɵɣ ɩɟɪɟɯɨɞ ɜɬɨɪɨɝɨ ɪɨɞɚ
Ʉɚɤ ɨɬɦɟɱɚɥɨɫɶ ɩɪɢ ɜɵɜɨɞɟ ɨɛɦɟɧɧɨɝɨ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ
ɜɝɥ. 1, ɞɥɹ ɚɧɫɚɦɛɥɹ ɨɞɢɧɚɤɨɜɵɯ ɤɜɚɧɬɨɜɵɯ ɱɚɫɬɢɰ ɞɨɥɠɟɧ
ɜɵɩɨɥɧɹɬɶɫɹ ɩɪɢɧɰɢɩ ɬɨɠɞɟɫɬɜɟɧɧɨɫɬɢ, ɬ.ɟ. ɫɨɫɬɨɹɧɢɹ ɫɢɫɬɟ-
ɦɵ, ɩɨɥɭɱɚɸɳɢɟɫɹ ɞɪɭɝ ɢɡ ɞɪɭɝɚ ɩɪɨɫɬɨ ɩɟɪɟɫɬɚɧɨɜɤɨɣ ɤɨɨɪ-
ɞɢɧɚɬ ɱɚɫɬɢɰ, ɞɨɥɠɧɵ ɛɵɬɶ ɮɢɡɢɱɟɫɤɢ ɩɨɥɧɨɫɬɶɸ ɷɤɜɢɜɚɥɟɧɬ-
ɧɵ. ɗɬɨ ɡɧɚɱɢɬ, ɱɬɨ ɜ ɪɟɡɭɥɶɬɚɬɟ ɬɚɤɨɣ ɩɟɪɟɫɬɚɧɨɜɤɢ ɜɨɥɧɨɜɚɹ
ɮɭɧɤɰɢɹ ɫɢɫɬɟɦɵ ɦɨɠɟɬ ɢɡɦɟɧɢɬɶɫɹ ɬɨɥɶɤɨ ɧɚ ɧɟɫɭɳɟɫɬɜɟɧ-
ɧɵɣ ɮɚɡɨɜɵɣ ɦɧɨɠɢɬɟɥɶ.
Ⱦɪɭɝɢɦɢ ɫɥɨɜɚɦɢ, ɟɫɥɢ
|
<
(1,2)|
2
=|
<
(2,1)|
2
, ɬɨ
<
(1,2)=exp(i
D
)
<
(2,1), ɝɞɟ
D
- ɜɟɳɟɫɬ-
ɜɟɧɧɚɹ ɩɨɫɬɨɹɧɧɚɹ. ɉɨɜɬɨɪɧɚɹ ɩɟɪɟɫɬɚɧɨɜɤɚ ɞɚɟɬ exp(2i
D
=1,
ɬɨ ɟɫɬɶ
<
(1,2)=r
<
(2,1). ɉɨɷɬɨɦɭ ɜɨɥɧɨɜɚɹ ɮɭɧɤɰɢɹ ɥɢɛɨ ɫɢɦ-
ɦɟɬɪɢɱɧɚ ( ɷɬɨ ɫɬɚɬɢɫɬɢɤɚ Ȼɨɡɟ), ɥɢɛɨ ɚɧɬɢɫɢɦɦɟɬɪɢɱɧɚ (ɷɬɨ
ɫɬɚɬɢɫɬɢɤɚ Ɏɟɪɦɢ). ɗɬɨɬ ɮɚɤɬ ɨɬɪɚɠɚɟɬɫɹ ɧɚ ɫɨɨɬɧɨɲɟɧɢɹɯ
ɤɨɦɦɭɬɚɰɢɢ ɩɪɢ ɨɩɢɫɚɧɢɢ ɫɢɫɬɟɦɵ ɜ ɬɟɪɦɢɧɚɯ ɜɬɨɪɢɱɧɨ-
ɤɜɚɧɬɨɜɚɧɧɵɯ ɨɩɟɪɚɬɨɪɨɜ, ɚ ɬɚɤɠɟ ɧɚ ɜɢɞɟ ɮɭɧɤɰɢɢ ɪɚɫɩɪɟɞɟ-
