Электротехника и электроника
Подождите немного. Документ загружается.

51
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
4. ÏÅÐÈÎÄÈ×ÅÑÊÈÅ ÍÅÑÈÍÓÑÎÈÄÀËÜÍÛÅ ÒÎÊÈ
 ÝËÅÊÒÐÈ×ÅÑÊÈÕ ÖÅÏßÕ
4.1. Äåéñòâóþùåå çíà÷åíèå ïåðèîäè÷åñêîãî
íåñèíóñîèäàëüíîãî òîêà
4.1.1. Ïåðèîäè÷åñêèå íåñèíóñîèäàëüíûå òîêè
(íàïðÿæåíèÿ, ÝÄÑ)
Òîêè è íàïðÿæåíèÿ â çíà÷èòåëüíîé ÷àñòè ýëåêòðè÷åñêèõ óñòðîéñòâ, è
ïðåæäå âñåãî â ýíåðãåòè÷åñêèõ óñòàíîâêàõ, ìîæíî ñ÷èòàòü ñèíóñîèäàëüíûìè.
Îäíàêî, â ðÿäå ñëó÷àåâ, òîêè è íàïðÿæåíèÿ îòëè÷àþòñÿ îò ñèíóñîèäàëüíûõ.
Ïðè÷èíîé ïîÿâëåíèÿ íåñèíóñîèäàëüíûõ íàïðÿæåíèé è òîêîâ ìîãóò áûòü êàê
ãåíåðàòîðû, òàê è ïðèåìíèêè ýíåðãèè.  ìàøèííûõ ãåíåðàòîðàõ îäíîé èç ïðè÷èí
èñêàæåíèÿ ôîðìû êðèâîé ÝÄÑ ÿâëÿåòñÿ íåñèíóñîèäàëüíîå ðàñïðåäåëåíèå
ìàãíèòíîé èíäóêöèè â âîçäóøíîì çàçîðå èç-çà íàëè÷èÿ ó ÿêîðÿ çóáöîâ è
âïàäèí, ðåàêöèè ÿêîðÿ.
 ïðèåìíèêàõ ýíåðãèè íåñèíóñîèäàëüíîñòü òîêà èëè íàïðÿæåíèÿ ìîæåò
áûòü âûçâàíà íåëèíåéíîé çàâèñèìîñòüþ ìåæäó ìàãíèòíûì ïîòîêîì è
íàìàãíè÷èâàþùèì òîêîì. Íåñèíóñîèäàëüíûå òîêè ïîÿâëÿþòñÿ â öåïè âî âñåõ
ñëó÷àÿõ ðàáîòû ïðèåìíèêîâ ýíåðãèè ñ íåëèíåéíûìè âîëüò-àìïåðíûìè
õàðàêòåðèñòèêàìè.
Ïåðèîäè÷åñêèå íåñèíóñîèäàëüíûå òîêè (íàïðÿæåíèÿ, ÝÄÑ) - òîêè
(íàïðÿæåíèÿ, ÝÄÑ), èçìåíÿþùèåñÿ âî âðåìåíè ïî ïåðèîäè÷åñêîìó
íåñèíóñîèäàëüíîìó çàêîíó.
4.1.2. Ïðåäñòàâëåíèå ïåðèîäè÷åñêèõ íåñèíóñîèäàëüíûõ
ýëåêòðè÷åñêèõ âåëè÷èí òðèãîíîìåòðè÷åñêèì ðÿäîì Ôóðüå
Ïðè èçó÷åíèè ïðîöåññîâ â ýëåêòðè÷åñêèõ öåïÿõ ñ íåñèíóñîèäàëüíûìè
òîêàìè è íàïðÿæåíèÿìè ìîæíî ïîëüçîâàòüñÿ òåîðåìîé Ôóðüå, ñîãëàñíî
êîòîðîé âñÿêàÿ ïåðèîäè÷åñêè èçìåíÿþùàÿñÿ âåëè÷èíà (òîê, íàïðÿæåíèå,
ÝÄÑ) ðàññìàòðèâàåòñÿ êàê ñóììà ïîñòîÿííîé, íåçàâèñèìîé îò âðåìåíè
âåëè÷èíû è ðÿäà ñèíóñîèäàëüíûõ (ãàðìîíè÷åñêèõ) âåëè÷èí ñ êðàòíûìè
÷àñòîòàìè. Ãàðìîíè÷åñêàÿ ñîñòàâëÿþùàÿ, ÷àñòîòà êîòîðîé ðàâíà ÷àñòîòå
íåñèíóñîèäàëüíîé ïåðèîäè÷åñêîé âåëè÷èíû, íàçûâàåòñÿ îñíîâíîé ãàðìîíèêîé.
Îñòàëüíûå ãàðìîíèêè, ó êîòîðûõ ÷àñòîòà â 2, 3, 4, 5 è ò.ä. ðàç áîëüøå,
íàçûâàþòñÿ âûñøèìè ãàðìîíèêàìè, ò.å. âòîðîé ãàðìîíèêîé, òðåòüåé è ò.ä.
Îòðåçîê îñè àáñöèññ, ñîîòâåòñòâóþùèé îäíîìó ïåðèîäó Ò = 2π / ω îñíîâíîé
ãàðìîíèêè, ðàâåí n ïåðèîäàì n-é ãàðìîíèêè. Ìàñøòàá ïî îñè àáñöèññ,
íàïðèìåð, äëÿ ïÿòîé ãàðìîíèêè (n=5) â 5 ðàç áîëüøå ìàñøòàáà îñíîâíîé
ãàðìîíèêè.
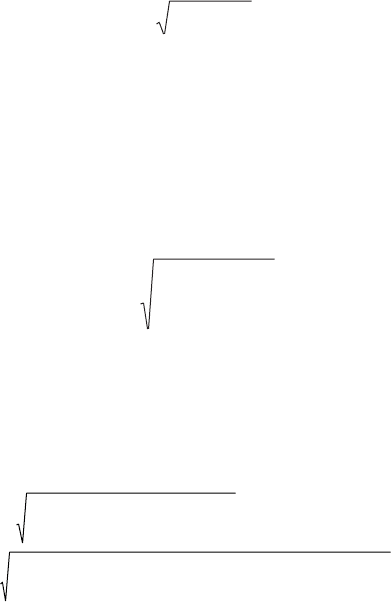
Âñÿêàÿ ïåðèîäè÷åñêè èçìåíÿþùàÿñÿ âåëè÷èíà ƒ( ωt ) èëè y( x ) ñ ïåðèîäîì
2π (òîê, íàïðÿæåíèå, ÝÄÑ) ìîæåò áûòü ðàçëîæåíà íà ïîñòîÿííóþ ñîñòàâëÿþùóþ
À
0
è ðÿä ñèíóñîèä:
ƒ( ωt ) = À
0
+ À
1
sin( ωt + ψ
1
) + À
2
sin( 2ωt + ψ
2
) + … ( 4.1 )
èëè y( x ) = À
0
+ À
1
sin( x + ϕ
1
) + À
2
sin( 2 x + ϕ
2
) + … , ( 4.2 )
ãäå À
0
ïîñòîÿííàÿ ñîñòàâëÿþùàÿ;
À
1
, À
2
… - àìïëèòóäû ãàðìîíèê ïåðâîé è ò.ä.;
ψ
1
, ψ
2
… - íà÷àëüíûå ôàçû.
52
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
Èñïîëüçóÿ âûðàæåíèå èç òðèãîíîìåòðèè äëÿ ñèíóñà êàê ñóììû äâóõ óãëîâ,
âûðàæåíèå äëÿ ëþáîé n-é ãàðìîíèêè çàïèøåòñÿ ñëåäóþùèì îáðàçîì:
A
n
sin( nx + ϕ
n
) = A
n
sin( nx ) cos( ϕ
n
) + A
n
cos( nx ) sin( ϕ
n
). ( 4.3 )
Åñëè îáîçíà÷èòü A
n
cos( ϕ
n
) = B
n
, à A
n
sin( ϕ
n
) = C
n
, òî äëÿ n-é ãàðìîíèêè
ïîëó÷èì:
A
n
sin( nx + ϕ
n
) = B
n
sin( nx ) + C
n
cos( nx ).
Òàêèì îáðàçîì, ðÿä ( 4.1 ) èëè ( 4.2 ) ìîæíî ïðåäñòàâèòü â âèäå ñóììû
ðÿäà ñèíóñîâ è ðÿäà êîñèíóñîâ ñ íóëåâûìè íà÷àëüíûìè ôàçàìè.
Äëÿ ðÿäà ( 4.2 ) èìååì:
y( x ) = À
0
+ Â
1
sin( x ) + Â
2
sin( 2 x ) + … + C
1
cos( x ) + C
2
cos( 2x ) +… ( 4.4 )
Åñëè ðÿäû ñèíóñîèä è êîñèíóñîèä ñ íóëåâûìè íà÷àëüíûìè ôàçàìè ( 4.4 )
íåîáõîäèìî çàìåíèòü îäíèì ðÿäîì ñèíóñîèä ñ íà÷àëüíûìè ôàçàìè, îòëè÷íûìè
îò íóëÿ, òî àìïëèòóäû ñèíóñîèä n-é ãàðìîíèêè çàïèøóòñÿ :
A
n
=
2
n
2
n
CÂ
+
,
íà÷àëüíàÿ ôàçà:
tg( ψ
n
) = C
n
/ Â
n
. ( 4.5 )
4.1.3. Äåéñòâóþùåå çíà÷åíèå ïåðèîäè÷åñêîãî íåñèíóñîèäàëüíîãî
òîêà (íàïðÿæåíèÿ, ÝÄÑ)
Äåéñòâóþùåå çíà÷åíèå ïåðèîäè÷åñêîãî íåñèíóñîèäàëüíîãî òîêà
(íàïðÿæåíèÿ èëè ÝÄÑ) ëþáîé ôîðìû îïðåäåëÿåòñÿ òàêèì æå âûðàæåíèåì,
êàê è äëÿ öåïè ñèíóñîèäàëüíîãî òîêà:
∫
ω=
2
ð
0
2
tdu1/2
ð
U
.
Ðàçëîæèâ ïåðèîäè÷åñêîå íàïðÿæåíèå íåñèíóñîèäàëüíîé ôîðìû â ðÿä,
ïîëó÷èì:
u = U
0
+ u
1
+ u
2
+ … = U
0
+ U
1m
sin( ωt + ψ
1
) + U
2m
sin( 2ωt + ψ
2
) + …
Ïîäñòàâèâ ýòîò ðÿä â ôîðìóëó äåéñòâóþùåãî çíà÷åíèÿ, ïîëó÷èì:
.dt...))t2sin(U)tsin(UU(T/1
dt...)uuuU(T/1U
T
0
2
2m21m10
2
3
T
0
210
∫
∫
+ψ+ω+ψ+ω+=
=++++=

53
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
Âîçâåäÿ â êâàäðàò ìíîãî÷ëåí, çàêëþ÷åííûé â êâàäðàòíûå ñêîáêè, ïîëó÷èì
íîâûé ìíîãî÷ëåí, ñîäåðæàùèé ñëàãàåìîå:
1) êâàäðàòû ïîñòîÿííîé ñîñòàâëÿþùåé è âñåõ ãàðìîíèê:
2
nm
2
0
U
;
U
sin( nωt + ψ
n
);
2) óäâîåííûå ïðîèçâåäåíèÿ êàæäîãî èç ÷ëåíîâ íà êàæäóþ äðóãóþ
ãàðìîíèêó:
2 U
0
U
nm
sin( nωt + ψ
n
) è
2 U
km
sin( kωt + ψ
k
) U
nm
sin( nωt + ψ
n
).
Èíòåãðèðîâàíèå ýòèõ ñëàãàåìûõ:
∫∫
=+=
T
0
2
k
2
kmk
2
km
T
0
2
0
2
0
;/2UU)dt
ø
sin(kwtU1/T;UdtU1/T
∫
=ψ+
T
0
nmn0
;
0dt
)
nwtsin
(
UU2T/1
.
0))dt
ø
sin(nwtU)
ø
(kwtsin(2U1/T
nnmk
T
0
km
=++
∫
Èç ÷åãî ñëåäóåò, ÷òî äåéñòâóþùåå çíà÷åíèå íåñèíóñîèäàëüíîãî
íàïðÿæåíèÿ ðàâíî:
,...UUUU
2
2
2
1
2
0
+++=
(4.6)
ãäå U
0
- ïîñòîÿííàÿ ñîñòàâëÿþùàÿ;
/2UU
2
1m
2
1
= è ò.ä. êâàäðàò äåéñòâóþùèõ çíà÷åíèé ñèíóñîèäàëüíûõ
ñîñòàâëÿþùèõ.
Àíàëîãè÷íûå âûðàæåíèÿ ïîëó÷àþòñÿ äëÿ íåñèíóñîèäàëüíûõ òîêà è ÝÄÑ.
4.1.4. Êîýôôèöèåíò ôîðìû ïåðèîäè÷åñêîé íåñèíóñîèäàëüíîé
êðèâîé òîêà (íàïðÿæåíèÿ, ÝÄÑ)
Ñîîòíîøåíèÿ ìåæäó àìïëèòóäàìè, äåéñòâóþùèìè è ñðåäíèìè çà ïîëîâèíó
ïåðèîäà çíà÷åíèÿìè ïåðèîäè÷åñêîãî òîêà (íàïðÿæåíèÿ è ÝÄÑ), êðèâûå êîòîðûõ
ñèììåòðè÷íû îòíîñèòåëüíî îñè àáñöèññ, îöåíèâàþòñÿ êîýôôèöèåíòàìè
ôîðìû dô è àìïëèòóäû dà.
Êîýôôèöèåíòîì ôîðìû íàçûâàåòñÿ îòíîøåíèå äåéñòâóþùåãî çíà÷åíèÿ
ê ñðåäíåìó:
äëÿ òîêà dô = I / Iñð;
äëÿ íàïðÿæåíèÿ dô = U / Uñð;
äëÿ ÝÄÑ dô = Å / Åñð.
ω
ω
ω
ω
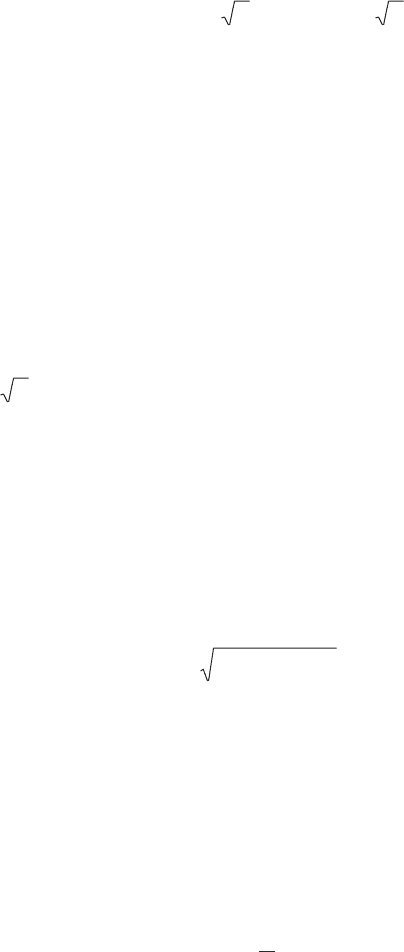
54
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
Äëÿ ñèíóñîèäàëüíî èçìåíÿþùèõñÿ âåëè÷èí êîýôôèöèåíò ôîðìû:
dô = I / Iñð = (I
m
·π ) / ( 2
2
I
m
) = π / ( 2
2
) = 1.1.
Åñëè ïåðèîäè÷åñêè èçìåíÿþùàÿñÿ âåëè÷èíà èìååò êðèâóþ áîëåå îñòðîé
ôîðìû, ÷åì ñèíóñîèäà, òî êîýôôèöèåíò ôîðìû dô > 1.1; äëÿ êðèâûõ áîëåå
ïîëîãîé ôîðìû, ÷åì ñèíóñîèäà dô < 1.1.
Ïðèìåíÿÿ êîýôôèöèåíò ôîðìû, ìîæíî äåéñòâóþùåå çíà÷åíèå ÝÄÑ
âûðàçèòü ÷åðåç ìàêñèìàëüíîå çíà÷åíèå ìàãíèòíîãî ïîòîêà, èíäóöèðóþùåãî
ýòó ÝÄÑ:
Å = dô Åñð = 4 dô ω fΦmax.
4.1.5. Êîýôôèöèåíò àìïëèòóäû
Êîýôôèöèåíòîì àìïëèòóäû íàçûâàåòñÿ îòíîøåíèå ìàêñèìàëüíîãî
çíà÷åíèÿ ê äåéñòâóþùåìó:
äëÿ òîêà dà = I max / I;
äëÿ íàïðÿæåíèÿ dà = Umax / U;
äëÿ ÝÄÑ dà = Åmax / Å.
Äëÿ ñèíóñîèäàëüíî èçìåíÿþùèõñÿ âåëè÷èí êîýôôèöèåíò àìïëèòóäû
dà = I
m
/ I =
2
= 1.41.
Äëÿ ïåðèîäè÷åñêè èçìåíÿþùèõñÿ âåëè÷èí ñ ãðàôèêîì, áîëåå îñòðûì,
÷åì ñèíóñîèäà dà > 1.41, äëÿ áîëåå ïîëîãîãî, ÷åì ñèíóñîèäà, ãðàôèêà,
dà < 1.14.
4.1.6. Êîýôôèöèåíò èñêàæåíèÿ
Ñòåïåíü íåñèíóñîèäàëüíîñòè êðèâûõ íàïðÿæåíèÿ è òîêà, â áîëüøåé èëè
ìåíüøåé ñòåïåíè îòëè÷àþùèõñÿ îò ñèíóñîèäàëüíîé êðèâîé èç-çà íàëè÷èÿ
âûñøèõ ãàðìîíèê, îöåíèâàåòñÿ êîýôôèöèåíòîì èñêàæåíèÿ. Êîýôôèöèåíòîì
èñêàæåíèÿ íàçûâàåòñÿ îòíîøåíèå äåéñòâóþùåãî çíà÷åíèÿ îñíîâíîé ãàðìîíèêè
ê äåéñòâóþùåìó çíà÷åíèþ.
Äëÿ íàïðÿæåíèÿ êîýôôèöèåíò èñêàæåíèÿ ðàâåí:
du = U
1
/ (
...UU
2
1
2
0
++
). ( 4.7 )
Àíàëîãè÷íî äëÿ òîêà è ÝÄÑ.
×åì ìåíüøå êîýôôèöèåíò èñêàæåíèÿ îòëè÷àåòñÿ îò åäèíèöû, òåì áëèæå
ê ñèíóñîèäå äàííàÿ êðèâàÿ.
4.2. Ìîùíîñòü ïåðèîäè÷åñêîãî íåñèíóñîèäàëüíîãî òîêà
4.2.1. Àêòèâíàÿ ìîùíîñòü ïåðèîäè÷åñêîãî íåñèíóñîèäàëüíîãî òîêà
Àêòèâíàÿ ìîùíîñòü ïðè íåñèíóñîèäàëüíîì òîêå èçìåðÿåòñÿ, êàê è
â ñëó÷àå ñèíóñîèäàëüíîãî òîêà, îòíîøåíèåì èçðàñõîäîâàííîé â öåïè çà ïåðèîä
ýíåðãèè ê ïðîäîëæèòåëüíîñòè ïåðèîäà:
.
∫∫
==
T
0
T
0
dtui
T
1
pdt1/TP
(4.8)
55
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
Ïîäñòàâèâ â ( 4.8 ) ìãíîâåííûå çíà÷åíèÿ íåñèíóñîèäàëüíûõ íàïðÿæåíèé
è òîêà, ïîëó÷èì:
P = 1/T
∫
T
0
[U
0
+U
1m
sin(ωt +ψ
1
)+U
2m
sin(2ωt +ψ
2
)+…]
⋅
[I
0
+I
1m
sin(ωt +ψ
1
-ϕ)+U
2m
sin(2ωt +ψ
2
−ϕ
2
)+…] dt.
Ïåðåìíîæèâ ìíîãî÷ëåí â êâàäðàòíûõ ñêîáêàõ, ïîëó÷èì èíòåãðàëû
ñëåäóþùèõ òèïîâ:
1) èíòåãðàë îò ïðîèçâåäåíèÿ ïîñòîÿííûõ âåëè÷èí:
1/T
∫
T
0
U
0
I
0
dt = U
0
I
0
;
2) èíòåãðàëû îò ïðîèçâåäåíèÿ äâóõ ñèíóñîèä îäíîé è òîé æå ÷àñòîòû:
1/T
∫
T
0
U
km
sin(kω t+ψ
k
) I
km
sin(kω t+ ψ
k
-ϕ
k
)] dt = U
k
I
k
cos(ϕ
k
) ;
3) èíòåãðàëû îò ïðîèçâåäåíèÿ ïîñòîÿííîé âåëè÷èíû è ñèíóñîèäû:
1/T
∫
T
0
U
0
I
km
sin(kωt+ψ
k
−ϕ
k
) dt=0;
1/T
∫
T
0
I
0
U
km
sin(kωt+ψ
k
) dt=0;
4) èíòåãðàëû îò ïðîèçâåäåíèÿ äâóõ ñèíóñîèä ñ ÷àñòîòàìè ðàçëè÷íûõ
ãàðìîíèê. Ýòè èíòåãðàëû ðàâíû íóëþ.
Àêòèâíàÿ ìîùíîñòü ðàâíà:
P = U
0
I
0
+ U
1
I
1
cos(ϕ
1
) + U
2
I
2
cos (ϕ
2
) + …= P
0
+ P
1
+ P
2
+ …
Ñðåäíÿÿ èëè àêòèâíàÿ ìîùíîñòü íåñèíóñîèäàëüíîãî òîêà ðàâíà ñóììå
àêòèâíûõ ìîùíîñòåé îòäåëüíûõ ãàðìîíèê.
56
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
5. ÏÅÐÅÕÎÄÍÛÅ ÏÐÎÖÅÑÑÛ Â ËÈÍÅÉÍÛÕ
ÝËÅÊÒÐÈ×ÅÑÊÈÕ ÖÅÏßÕ
5.1. Çàêîíû êîììóòàöèè
5.1.1. Óñòàíîâèâøèéñÿ ðåæèì
Õàðàêòåð ïðîöåññîâ â ýëåêòðè÷åñêîé öåïè èëè åå ðåæèì çàâèñèò êàê îò
ïàðàìåòðîâ èñòî÷íèêà ýíåðãèè, òàê è îò ïàðàìåòðîâ ïàññèâíûõ ýëåìåíòîâ R,
L, C. Ïðè ëþáûõ èçìåíåíèÿõ çíà÷åíèé óêàçàííûõ âåëè÷èí èçìåíÿþòñÿ òîêè è
íàïðÿæåíèÿ â öåïè, à ñ íèìè è êîëè÷åñòâî ýíåðãèè, çàïàñàåìîé â åå ýëåìåíòàõ.
Åñëè ðàññìàòðèâàòü ëèíåéíûå öåïè, â êîòîðûõ ñîïðîòèâëåíèÿ ðåçèñòîðîâ,
èíäóêòèâíîñòè êàòóøåê è åìêîñòè êîíäåíñàòîðîâ ïîñòîÿííû, òî â òàêèõ öåïÿõ
èçìåíåíèÿ òîêîâ è íàïðÿæåíèé ïðîèñõîäÿò òîëüêî ïðè èçìåíåíèè íàïðÿæåíèé
èëè òîêîâ èñòî÷íèêîâ ýíåðãèè. Ïðè ýòîì ïðèíöèïèàëüíóþ ðîëü èãðàåò çíà÷åíèå
ñðåäíåãî çàïàñà ýíåðãèè â öåïè. Åñëè ñðåäíèé çàïàñ ýíåðãèè îñòàåòñÿ
íåèçìåííûì, â öåïè íàáëþäàåòñÿ óñòàíîâèâøèéñÿ ðåæèì, åñëè â öåïè çàïàñ
ýíåðãèè èçìåíÿåòñÿ, òî â öåïè íàáëþäàåòñÿ íåóñòàíîâèâøèéñÿ èëè
ïåðåõîäíûé ðåæèì. Ïðè äîñòàòî÷íî äëèòåëüíîì âîçäåéñòâèè ïîñòîÿííûõ ÝÄÑ
è òîêîâ ðåæèì áóäåò óñòàíîâèâøèìñÿ. Óñòàíîâèâøèéñÿ ðåæèì íàáëþäàåòñÿ
è ïðè ñêîëü óãîäíî áûñòðûõ, íî ïåðèîäè÷åñêèõ èçìåíåíèÿõ íàïðÿæåíèé,
èñòî÷íèêîâ ÝÄÑ èëè òîêîâ èñòî÷íèêîâ òîêà, êîãäà ñðåäíèé çàïàñ ýíåðãèè â
öåïè îñòàåòñÿ ïîñòîÿííûì. Åñëè áûòü òî÷íûì, òî ðåæèì ÿâëÿåòñÿ
óñòàíîâèâøèìñÿ òîëüêî â òîì ñëó÷àå, åñëè îí ïðîäîëæàåòñÿ áåñêîíå÷íî äîëãî,
à âñÿêèé ðåàëüíûé ïðîöåññ âñåãäà èìååò íà÷àëî è êîíåö, ïîýòîìó ïðîöåññû
ìîæíî ñ÷èòàòü óñòàíîâèâøèìèñÿ òîëüêî äëÿ ñòðîãî îïðåäåëåííûõ âðåìåííûõ
èíòåðâàëîâ. Óñòàíîâèâøèéñÿ ðåæèì ÿâëÿåòñÿ ÷àñòíûì ñëó÷àåì
íåóñòàíîâèâøåãîñÿ.
5.1.2. Êîììóòàöèÿ
 òåîðèè öåïåé ëþáûå âêëþ÷åíèÿ è âûêëþ÷åíèÿ èñòî÷íèêîâ ýíåðãèè,
âíåçàïíûå èçìåíåíèÿ ïàðàìåòðîâ ïàññèâíûõ ýëåìåíòîâ è ñõåìû öåïè,
ñêà÷êîîáðàçíûå èçìåíåíèÿ ÝÄÑ è òîêîâ ïðèíÿòî íàçûâàòü êîììóòàöèÿìè.
 îáùåì ñëó÷àå êàæäàÿ êîììóòàöèÿ ïðèâîäèò ê ïåðåõîäíîìó ïðîöåññó,
êîòîðûé ÿâëÿåòñÿ ïðîìåæóòî÷íûì ìåæäó äâóìÿ óñòàíîâèâøèìèñÿ.  ðåàëüíûõ
öåïÿõ òàêîé ïåðåõîä ïðîèñõîäèò íå ìãíîâåííî, òàê êàê ýòî òðåáóåò èçìåíåíèÿ
ýíåðãåòè÷åñêîãî ñîñòîÿíèÿ öåïè, ÷òî ñâÿçàíî ñ íàðàñòàíèåì èëè óáûâàíèåì
ýëåêòðîìàãíèòíîé ýíåðãèè.
5.1.3. Ïåðåõîäíûé ýëåêòðîìàãíèòíûé ïðîöåññ
Ïåðåõîäíûé ýëåêòðîìàãíèòíûé ïðîöåññ ïðîöåññ, êîòîðûé ÿâëÿåòñÿ
ïðîìåæóòî÷íûì ìåæäó äâóìÿ óñòàíîâèâøèìèñÿ. Ïðèâåñòè ê ïåðåõîäíîìó
ïðîöåññó ìîæåò ñêà÷êîîáðàçíîå èçìåíåíèå ÝÄÑ, èçìåíåíèå ïàðàìåòðîâ
ïàññèâíûõ ýëåìåíòîâ, ëþáûå âêëþ÷åíèÿ è âûêëþ÷åíèÿ èñòî÷íèêîâ ýíåðãèè.
Ìîùíîñòü èñòî÷íèêîâ ýíåðãèè îãðàíè÷åíà, ò.ê. îíà ÿâëÿåòñÿ ïðîèçâîäíîé
ýíåðãèè ïî âðåìåíè, è ñêà÷êîîáðàçíîå èçìåíåíèå ýíåðãèè òðåáóåò áåñêîíå÷íî
áîëüøîé ìîùíîñòè èñòî÷íèêîâ ýíåðãèè ýòî îçíà÷àåò, ÷òî ïåðåõîäíûé
ïðîöåññ òåîðåòè÷åñêè èìååò áåñêîíå÷íóþ äëèòåëüíîñòü.
Ïðàêòè÷åñêè çà êîðîòêèé ïðîìåæóòîê âðåìåíè çíà÷åíèÿ òîêîâ è
íàïðÿæåíèé ñòàíîâÿòñÿ íàñòîëüêî áëèçêèìè ê óñòàíîâèâøèìñÿ, ÷òî ïåðåõîäíûå
ïðîöåññû ìîæíî ñ÷èòàòü êîíå÷íûìè ïî äëèòåëüíîñòè. Àíàëèç ïåðåõîäíûõ
ïðîöåññîâ çíà÷èòåëüíî ñëîæíåå óñòàíîâèâøèõñÿ. Ýòî ñâÿçàíî ñ òåì, ÷òî
57
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
îïðåäåëåíèå òîêîâ è íàïðÿæåíèé â óñòàíîâèâøåìñÿ ðåæèìå ñâîäèòñÿ ê
ðåøåíèþ àëãåáðàè÷åñêèõ óðàâíåíèé èëè íàõîæäåíèþ ÷àñòíûõ ðåøåíèé
äèôôåðåíöèàëüíûõ óðàâíåíèé. Àíàëèç ïåðåõîäíûõ ïðîöåññîâ ïðîâîäèòñÿ â
äâà ýòàïà ñíà÷àëà ñòðîÿò ñõåìó çàìåùåíèÿ, çàòåì ñîñòàâëÿþò
äèôôåðåíöèàëüíûå óðàâíåíèÿ, îïèñûâàþùèå ïðîöåññû â ýòîé ñõåìå. Ïðè
ïîñòðîåíèè ñõåìû äåëàþò äâà äîïóùåíèÿ.
1) Ïðè êîììóòàöèÿõ âîçìîæíû ðåçêèå èçìåíåíèÿ òîêîâ è íàïðÿæåíèé,
êîãäà ñîïðîòèâëåíèÿ ðåçèñòîðîâ, åìêîñòè êîíäåíñàòîðîâ è èíäóêòèâíîñòè
êàòóøåê çàâèñÿò îò òîêà è íàïðÿæåíèÿ. Ïîýòîìó òî÷íîå îïèñàíèå ïåðåõîäíîãî
ïðîöåññà äîëæíî ïðîâîäèòñÿ ñ ïîìîùüþ íåëèíåéíûõ äèôôåðåíöèàëüíûõ
óðàâíåíèé. Ó÷åò íåëèíåéíîñòè ïàññèâíûõ ýëåìåíòîâ íåîïðàâäàííî óñëîæíÿåò
àíàëèç. Ïðè èññëåäîâàíèè ïåðåõîäíûõ ïðîöåññîâ ïðèíèìàþò, ÷òî ïàðàìåòðû
âñåõ ïàññèâíûõ ýëåìåíòîâ ïîñòîÿííû. Çàäà÷ó ñâîäÿò ê ëèíåéíîé.
2) Ðåàëüíûé ïðîöåññ êîììóòàöèè âñåãäà èìååò êîíå÷íûé ïðîìåæóòîê
âðåìåíè
∆t
k
.  òåîðèè öåïåé â áîëüøèíñòâå ñëó÷àåâ ïîëó÷àþò, ÷òî êîììóòàöèÿ
ïðîèñõîäèò ìãíîâåííî. Ñ÷èòàþò, ÷òî
∆t
k
=0. Ìîìåíò êîììóòàöèè ïðèíèìàþò çà
íà÷àëî ïåðåõîäíîãî ïðîöåññà t = 0 è ôèêñèðóþò çíà÷åíèå òîãî èëè èíîãî
òîêà, íàïðÿæåíèÿ â ìîìåíò, íåïîñðåäñòâåííî ïðåäøåñòâóþùèé êîììóòàöèè,
i(0
), u(0
) è â ìîìåíò, íåïîñðåäñòâåííî ñëåäóþùèé çà êîììóòàöèåé, i(0
+
),
u(0
+
).
Ïîëàãàþò, ÷òî êîììóòàöèÿ îñóùåñòâëÿåòñÿ ñ ïîìîùüþ èäåàëüíûõ êëþ÷åé
äâóõïîëîñíèêîâ, ñîïðîòèâëåíèå êîòîðûõ ðàâíî íóëþ, êîãäà êëþ÷ íàõîäèòñÿ
â çàìêíóòîì ñîñòîÿíèè, è áåñêîíå÷íîñòè, êîãäà êëþ÷ ðàçîìêíóò. Ïðèíÿòî, ÷òî
ñõåìû, ñ ïîìîùüþ êîòîðûõ àíàëèçèðóþòñÿ ïåðåõîäíûå ïðîöåññû,
èçîáðàæàþòñÿ äî êîììóòàöèè.
5.1.4. Îáîáùåííûé çàêîí êîììóòàöèè
 îñíîâå ðàñ÷åòîâ ïåðåõîäíûõ ïðîöåññîâ ëåæàò çàêîíû êîììóòàöèè.
Ïðè àíàëèçå ïåðåõîäíûõ ïðîöåññîâ â öåïÿõ äîïóñêàåòñÿ, ÷òî ýíåðãèÿ
ìàãíèòíîãî ïîëÿ ñâÿçàíà òîëüêî ñ êàòóøêàìè èíäóêòèâíîñòè, à ýíåðãèÿ
ýëåêòðè÷åñêîãî ïîëÿ ñ êîíäåíñàòîðàìè.  ñâÿçè ñ òåì, ÷òî ëþáîé ðåàëüíûé
èñòî÷íèê ýíåðãèè ìîæåò îòäàâàòü òîëüêî êîíå÷íóþ ìîùíîñòü, ñóììàðíàÿ
ýíåðãèÿ, çàïàñåííàÿ â öåïè, ìîæåò èçìåíÿòüñÿ òîëüêî ïëàâíî. Ïîýòîìó ïðè
ïåðåõîäå ê ñõåìå ñ÷èòàþò, ÷òî íà èíäóêòèâíîì ýëåìåíòå íå ìîæåò áûòü
áåñêîíå÷íî áîëüøîãî íàïðÿæåíèÿ, à ÷åðåç åìêîñòíîé ýëåìåíò íå ìîæåò
ïðîõîäèòü áåñêîíå÷íî áîëüøîé òîê. Ñëåäîâàòåëüíî, ïîòîêîñöåïëåíèå
èíäóêòèâíîãî ýëåìåíòà è çàðÿä åìêîñòíîãî ýëåìåíòà íåïðåðûâíû âî âðåìåíè.
Äëÿ ìîìåíòà êîììóòàöèè ýòî ïîëîæåíèå èçâåñòíî êàê îáîáùåííûé çàêîí
êîììóòàöèè: ïîòîêîñöåïëåíèå êàæäîãî èíäóêòèâíîãî ýëåìåíòà è çàðÿä êàæäîãî
åìêîñòíîãî ýëåìåíòà â ìîìåíò âðåìåíè êîììóòàöèè t = 0 ðàâíû òåì
çíà÷åíèÿì, êîòîðûå îíè èìåëè íåïîñðåäñòâåííî ïåðåä êîììóòàöèåé:
ψ(0
) = ψ(0
+
) èëè (L
) i(0
) = (L
+
) i(0
+
); (5.1)
q(0
) = q(0
+
) èëè (C
) i(0
) = (C
+
) i(0
+
). (5.2)
5.1.5. Ïåðâûé çàêîí êîììóòàöèè
Ïåðâûé çàêîí êîììóòàöèè ãëàñèò: åñëè â ïðîöåññå êîììóòàöèè
ñîáñòâåííûå èíäóêòèâíîñòè íå èçìåíÿþòñÿ (L
=L
+
), òî â ìîìåíò êîììóòàöèè
òîê, ïðîõîäÿùèé ÷åðåç èíäóêòèâíûé ýëåìåíò, ñîõðàíÿåò òî çíà÷åíèå, êîòîðîå
îí èìååò íåïîñðåäñòâåííî ïåðåä êîììóòàöèåé, è â äàëüíåéøåì èçìåíÿåòñÿ,
58
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
íà÷èíàÿ èìåííî ñ ýòîãî çíà÷åíèÿ:
i
LK
(0
)=i
LK
(0
+
). (5.3)
5.1.6. Âòîðîé çàêîí êîììóòàöèè
Âòîðîé çàêîí êîììóòàöèè ãëàñèò: åñëè â ïðîöåññå êîììóòàöèè
ñîáñòâåííûå åìêîñòè íå èçìåíÿþòñÿ (C
=C
+
), òî â ìîìåíò êîììóòàöèè
íàïðÿæåíèå íà åìêîñòíîì ýëåìåíòå ñîõðàíÿåò òî çíà÷åíèå, êîòîðîå îíî èìåëî
íåïîñðåäñòâåííî ïåðåä êîììóòàöèåé, è â äàëüíåéøåì èçìåíÿåòñÿ, íà÷èíàÿ
ñ ýòîãî çíà÷åíèÿ:
u
ñê
(0
)=u
ñê
(0
+
). (5.4)
Èç çàêîíîâ êîììóòàöèè ñëåäóåò, ÷òî òîê â èíäóêòèâíîì ýëåìåíòå è
íàïðÿæåíèå íà åìêîñòíîì ýëåìåíòå íå ìîãóò èçìåíÿòüñÿ ñêà÷êîîáðàçíî. Íî
íàïðÿæåíèå íà èíäóêòèâíîì ýëåìåíòå, òîê ÷åðåç åìêîñòíîé ýëåìåíò è òîê ñ
íàïðÿæåíèåì íà ðåçèñòèâíîì ýëåìåíòå èìåþò ïðàâî èçìåíÿòüñÿ ñêà÷êîì.
5.1.7. Ñâîáîäíûå ñîñòàâëÿþùèå òîêà (íàïðÿæåíèÿ)
Êëàññè÷åñêèé ìåòîä àíàëèçà ïåðåõîäíûõ ïðîöåññîâ îñíîâàí íà
íåïîñðåäñòâåííîì ðåøåíèè îáûêíîâåííûõ äèôôåðåíöèàëüíûõ óðàâíåíèé.
Ðåøåíèå ëèíåéíîãî íåîäíîðîäíîãî äèôôåðåíöèàëüíîãî óðàâíåíèÿ ñ
ïîñòîÿííûìè êîýôôèöèåíòàìè èùåòñÿ â âèäå ñóììû äâóõ ôóíêöèé:
y(t) = y
1
(t) + y
2
(t), (5.5)
ãäå y
1
(t) - îáùåå ðåøåíèå îäíîðîäíîãî äèôôåðåíöèàëüíîãî óðàâíåíèÿ
ïðè ƒ(t) = 0
a
n
d
n
y(t) / dt
n
+ a
n-1
d
n-1
y(t) / dt
n-1
+…+a
1
dy / dt + a
0
y(t) = ƒ(t)=0. (5.6)
y
2
(t ) ïðåäñòàâëÿåò ñîáîé ÷àñòíîå ðåøåíèå óðàâíåíèÿ:
a
n
d
n
y(t) / dt
n
+…+ a
1
dy(t)/dt +a
0
y(t) = ƒ(t).
Ôóíêöèÿ y
1
(t) íå çàâèñèò îò âèäà ïðàâîé ÷àñòè óðàâíåíèÿ. Îíà îïèñûâàåò
ýëåêòðè÷åñêèå ïðîöåññû â àíàëèçèðóåìîé ñõåìå ïîñëå êîììóòàöèè â
îòñóòñòâèå èñòî÷íèêîâ ýíåðãèè, ïîýòîìó â òåîðèè öåïåé îíà íàçûâàåòñÿ
ñâîáîäíîé ñîñòàâëÿþùåé y
ñâ
(t). Ôóíêöèÿ y
2
(t) îïðåäåëÿåòñÿ âèäîì ïðàâîé
÷àñòè óðàâíåíèÿ. Îíà çàâèñèò îò âíåøíèõ èñòî÷íèêîâ ýíåðãèè. Îíà íàçûâàåòñÿ
ïðèíóæäåííîé, èëè óñòàíîâèâøåéñÿ, ñîñòàâëÿþùåé y
ïð
(t). Êàê y
ñâ
(t), òàê è
y
ïð
(t) îòäåëüíî íå ñóùåñòâóþò, ïðèíóæäåííàÿ è ñâîáîäíàÿ ñîñòàâëÿþùèå
ÿâëÿþòñÿ ëèøü ðàñ÷åòíûìè âåëè÷èíàìè, èñïîëüçóåìûìè ïðè àíàëèçå
ïåðåõîäíûõ ïðîöåññîâ êëàññè÷åñêèì ìåòîäîì. Ò.ê. íà÷àëüíûé çàïàñ ýíåðãèè
â ëþáîé ýëåêòðè÷åñêîé öåïè îãðàíè÷åí, ñâîáîäíàÿ ñîñòàâëÿþùàÿ â öåïÿõ ñ
ïîòåðÿìè ñ òå÷åíèåì âðåìåíè çàòóõàåò: lim y
ñâ
(t)=0 , íîâûé óñòàíîâèâøèéñÿ
ðåæèì ïðåäñòàâëÿåò ñîáîé ïðèíóæäåííóþ ñîñòàâëÿþùóþ â ñõåìå ïîñëå
êîììóòàöèè.
Ñâîáîäíàÿ ñîñòàâëÿþùàÿ òîêà îïèñûâàåò ïðîòåêàíèå òîêà â
àíàëèçèðóåìîé ñõåìå ïîñëå êîììóòàöèè â îòñóòñòâèè èñòî÷íèêà ýíåðãèè.
59
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
5.1.8. Óñòàíîâèâøèéñÿ òîê (íàïðÿæåíèå)
Åñëè â òå÷åíèå äëèòåëüíîãî âðåìåíè òîêè (íàïðÿæåíèÿ) îñòàþòñÿ
ïîñòîÿííûìè èëè èçìåíÿþòñÿ ïåðèîäè÷åñêè, òî â öåïè íàáëþäàåòñÿ
óñòàíîâèâøèéñÿ ðåæèì. Òàêîé ðåæèì öåïè óñòàíàâëèâàåòñÿ ïðè äîñòàòî÷íî
äëèòåëüíîì äåéñòâèè èñòî÷íèêîâ ïîñòîÿííîé èëè ïåðèîäè÷åñêîé (â ÷àñòíîñòè,
ñèíóñîèäàëüíîé) ÝÄÑ íå ìãíîâåííî âñëåä çà ìîìåíòîì âêëþ÷åíèÿ èëè
îòêëþ÷åíèÿ èñòî÷íèêîâ ïèòàíèÿ, èëè ìîìåíòîì èçìåíåíèÿ åå ïàðàìåòðîâ (L,
C, R), ò.å. çà ìîìåíòîì êîììóòàöèè, ïîýòîìó óñòàíîâèâøèéñÿ òîê
(íàïðÿæåíèå) ýòî òîê (íàïðÿæåíèå) â ýëåêòðè÷åñêîé öåïè ïîñëå îêîí÷àíèÿ
ïåðåõîäíîãî ïðîöåññà.
5.1.9. Òîê (íàïðÿæåíèå) ïåðåõîäíîãî ïðîöåññà
Îäèí óñòàíîâèâøèéñÿ ðåæèì öåïè îòäåëÿåòñÿ îò äðóãîãî íåêîòîðûì
ïðîìåæóòêîì âðåìåíè, â òå÷åíèå êîòîðîãî ïðîèñõîäÿò ÿâëåíèÿ,
îáåñïå÷èâàþùèå ïîñòåïåííûé ïåðåõîä îò ïðåæíåãî ñîñòîÿíèÿ öåïè ê íîâîìó.
Èçó÷åíèå ïåðåõîäíûõ ïðîöåññîâ â ëèíåéíûõ öåïÿõ óïðîùàåòñÿ, åñëè
ïåðåõîäíûé ïðîöåññ ðàññìàòðèâàòü êàê ðåçóëüòàò íàëîæåíèÿ äâóõ ïðîöåññîâ
- óñòàíàâëèâàþùåãîñÿ ðåæèìà, ïîëàãàÿ, ÷òî îí íàñòóïàåò ìãíîâåííî ïîñëå
êîììóòàöèè, è ñâîáîäíîãî ïðîöåññà, îáåñïå÷èâàþùåãî ïåðåõîä öåïè îò
ïðåæíåãî óñòàíîâèâøåãîñÿ ðåæèìà ê íîâîìó óñòàíîâèâøåìóñÿ ðåæèìó.
Ñâîáîäíûé ïðîöåññ âîçíèêàåò ïîñëå êîììóòàöèè âñëåäñòâèå
íåñîîòâåòñòâèÿ ýíåðãèè, çàïàñåííîé â ìàãíèòíîì èëè ýëåêòðè÷åñêîì ïîëÿõ
öåïè, íîâîìó óñòàíîâèâøåìóñÿ ðåæèìó. Çíà÷åíèÿ ñâîáîäíûõ òîêîâ è
íàïðÿæåíèé çàâèñÿò îò óðîâíÿ íåñîîòâåòñòâèÿ ýíåðãèé ìàãíèòíîãî è
ýëåêòðè÷åñêîãî ïîëåé íîâîìó óñòàíîâèâøåìóñÿ ðåæèìó. Ïî ìåðå óìåíüøåíèÿ
ýòîãî íåñîîòâåòñòâèÿ ñâîáîäíûå òîêè è íàïðÿæåíèÿ ïîñòåïåííî óìåíüøàþòñÿ
äî íóëåâûõ çíà÷åíèé. Äåéñòâèòåëüíûé òîê â öåïè â òå÷åíèå ïåðåõîäíîãî
ïðîöåññà ìîæíî ïðåäñòàâèòü â âèäå ñóììû äâóõ ñîñòàâëÿþùèõ:
óñòàíîâèâøåãîñÿ íîâîãî òîêà è ñâîáîäíîãî òîêà:
i = i
ó
+ i
ñâ
. (5.7)
Àíàëîãè÷íî íàïðÿæåíèå â òå÷åíèå ïåðåõîäíîãî ïðîöåññà:
u = u
ó
+ u
ñâ
. (5.8)
5.2. Êëàññè÷åñêèé ìåòîä ðàñ÷åòà ïåðåõîäíûõ ïðîöåññîâ
5.2.1. Êëàññè÷åñêèé ìåòîä ðàñ÷åòà ïåðåõîäíîãî ïðîöåññà
â ýëåêòðè÷åñêîé öåïè
Ðàñ÷åò ïåðåõîäíûõ ïðîöåññîâ êëàññè÷åñêèì ìåòîäîì âûïîëíÿåòñÿ â
ñëåäóþùåé ïîñëåäîâàòåëüíîñòè:
1) Ñîñòàâëÿåòñÿ ñèñòåìà èíòåãðî-äèôôåðåíöèàëüíûõ óðàâíåíèé,
îïèñûâàþùèõ ïðîöåññû â ïîñëåêîììóòàöèîííîé ñõåìå.
2) Ðåøàåòñÿ ïîëó÷åííàÿ ñèñòåìà óðàâíåíèé îòíîñèòåëüíî îñíîâíîé
ïåðåìåííîé, ïîëó÷àþò ëèíåéíîå íåîäíîðîäíîå óðàâíåíèå n-ãî ïîðÿäêà
îòíîñèòåëüíî ýòîé ïåðåìåííîé.
3) Çàïèñûâàåòñÿ âèä ðåøåíèÿ äëÿ ñâîáîäíîé ñîñòàâëÿþùåé.
4) Ðàññ÷èòûâàåòñÿ óñòàíîâèâøàÿñÿ (ïðèíóæäåííàÿ) ñîñòàâëÿþùàÿ.
5) Îïðåäåëÿþòñÿ íà÷àëüíûå óñëîâèÿ.
6) Íàõîäÿòñÿ ïîñòîÿííûå èíòåãðèðîâàíèÿ.
60
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
7) Ïîëó÷àþò îêîí÷àòåëüíîå âûðàæåíèå äëÿ ïåðåõîäíîé ôóíêöèè y(t) -
îïðåäåëÿþò ìãíîâåííûå çíà÷åíèÿ îñíîâíîé ïåðåìåííîé äëÿ t> 0.
Àíàëèç öåïåé ñ îäíèì íàêîïèòåëåì ýíåðãèè (èíäóêòèâíîé êàòóøêîé èëè
êîíäåíñàòîðîì) ñâîäèòñÿ ê èññëåäîâàíèþ RL èëè RC ñõåì, ãäå ïåðåõîäíûå
ïðîöåññû îïèñûâàþòñÿ äèôôåðåíöèàëüíûìè óðàâíåíèÿìè ïåðâîãî ïîðÿäêà.
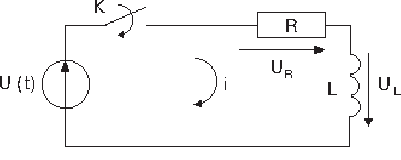
Ýëåêòðè÷åñêàÿ öåïü, ñîñòîÿùàÿ èç ïîñëåäîâàòåëüíî ñîåäèíåííûõ
ðåçèñòèâíîãî è èíäóêòèâíîãî ýëåìåíòîâ (ðèñ.5.1), â ìîìåíò âðåìåíè t=0
ïîäêëþ÷àåòñÿ ê èñòî÷íèêó íàïðÿæåíèÿ u(t).
Ðèñ.5.1
Äëÿ ñõåìû, îáðàçîâàâøåéñÿ ïîñëå êîììóòàöèè, ìîæíî çàïèñàòü
ñëåäóþùóþ ñèñòåìó óðàâíåíèé:
u
R
+ u
L
= u(t)
u
R
= R⋅i
u
L
= L⋅ di / dt.
 êà÷åñòâå îñíîâíîé ïåðåìåííîé âûáèðàåòñÿ òîê è èñêëþ÷àþòñÿ èç
ïîëó÷åííîé ñèñòåìû óðàâíåíèé âñå íåèçâåñòíûå, êðîìå i. Ïîñëå ýòîãî
äèôôåðåíöèàëüíîå óðàâíåíèå, îïèñûâàþùåå èçìåíåíèå îñíîâíîé
ïåðåìåííîé ïîñëå êîììóòàöèè, ïðèìåò âèä:
L⋅ di / dt + R⋅i = u(t). (5.9)
Ðåøåíèå ýòîãî óðàâíåíèÿ çàïèøåòñÿ â âèäå ñóììû ñâîáîäíîé è
óñòàíîâèâøåéñÿ ñîñòàâëÿþùèõ:
i(t) = i
ñâ
+ i
ó
.
Âûðàæåíèå äëÿ ñâîáîäíîé ñîñòàâëÿþùåé èìååò âèä i
ñâ
= A⋅ exp(-t/τ), ãäå
À ïîñòîÿííàÿ èíòåãðèðîâàíèÿ,
τ = L / R.
Âèä ðåøåíèÿ äëÿ óñòàíîâèâøåéñÿ ñîñòàâëÿþùåé òîêà i
y
çàâèñèò îò âèäà
ôóíêöèè u(t).
Äëÿ ñëó÷àÿ, êîãäà íàïðÿæåíèå èñòî÷íèêà ïîñòîÿííî, u(t) = Å = const,
óñòàíîâèâøàÿñÿ ñîñòàâëÿþùàÿ, ñîîòâåòñòâóþùàÿ íîâîìó óñòàíîâèâøåìóñÿ
çíà÷åíèþ òîêà â öåïè ïîñëå êîììóòàöèè, áóäåò ïîñòîÿííîé:
i
y
= E / R.
 ðàññìàòðèâàåìîì ñëó÷àå èñêîìûé òîê ðàâåí:
i(t) = i
y
+ i
cb
= E / R + A ⋅ exp ( -t / τ ). (5.10)
