Электротехника и электроника
Подождите немного. Документ загружается.

11
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
íàïðÿæåíèÿ íà êîíöàõ ó÷àñòêà öåïè ê òîêó â íåì:
R = U / I. (1.3)
Åäèíèöà ñîïðîòèâëåíèÿ íàçûâàåòñÿ Îì.
Èíäóêòèâíûì íàçûâàþò òàêîé ñõåìíûé ýëåìåíò, â êîòîðîì ïðîèñõîäèò
òîëüêî íàêîïëåíèå ìàãíèòíîé ýíåðãèè èëè òîëüêî îáìåí ìàãíèòíîé ýíåðãèåé
ñ öåïüþ.
Åìêîñòíûì íàçûâàþò òàêîé ñõåìíûé ýëåìåíò, â êîòîðîì ïðîèñõîäèò
òîëüêî íàêîïëåíèå ýëåêòðè÷åñêîé ýíåðãèè èëè òîëüêî îáìåí ýëåêòðè÷åñêîé
ýíåðãèåé ñ öåïüþ.
Êàæäûé ýëåìåíò õàðàêòåðèçóåòñÿ òîëüêî îäíèì ïàðàìåòðîì: ðåçèñòèâíûé
- ñîïðîòèâëåíèåì, èíäóêòèâíûé èíäóêòèâíîñòüþ, åìêîñòíûé åìêîñòüþ.
Âñå ýòè ïàðàìåòðû ìîãóò áûòü ëèáî ïîñòîÿííûìè, ëèáî çàâèñÿùèìè îò
çíà÷åíèé è íàïðàâëåíèé íàïðÿæåíèé è òîêîâ èëè îò âðåìåíè.
Àêòèâíûå ñõåìíûå ýëåìåíòû ïðåäñòàâëÿþò ñîáîé èñòî÷íèêè ýíåðãèè,
êîòîðûå ìîãóò áûòü íåçàâèñèìûìè è çàâèñèìûìè èëè óïðàâëÿåìûìè.
Íåçàâèñèìûì èñòî÷íèêîì ÝÄÑ íàçûâàþò äâóõïîëþñíèê, íàïðÿæåíèå íà
âûõîäíûõ çàæèìàõ êîòîðîãî çàäàíî äëÿ êàæäîãî ìîìåíòà âðåìåíè è íå çàâèñèò
îò ïðîõîäÿùåãî ÷åðåç íåãî òîêà. Íàïðÿæåíèå íà çàæèìàõ òàêîãî èñòî÷íèêà
U(t) ðàâíî åãî ÝÄÑ è ìîæåò áûòü ïðîèçâîëüíîé ôóíêöèåé âðåìåíè. Åñëè îíî
íå çàâèñèò îò âðåìåíè, òî èñòî÷íèê íàçûâàåòñÿ èñòî÷íèêîì ïîñòîÿííîé ÝÄÑ.
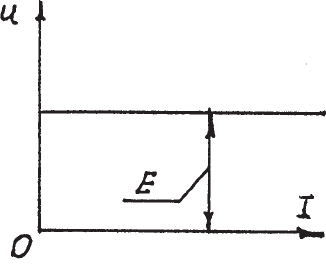
Îñíîâíîé õàðàêòåðèñòèêîé èñòî÷íèêà ÝÄÑ ÿâëÿåòñÿ âíåøíÿÿ
õàðàêòåðèñòèêà çàâèñèìîñòü íàïðÿæåíèÿ íà åãî çàæèìàõ îò îòäàâàåìîãî
èì òîêà. Äëÿ èñòî÷íèêà ïîñòîÿííîé ÝÄÑ âíåøíÿÿ õàðàêòåðèñòèêà ïðåäñòàâëÿåò
ñîáîé ïðÿìóþ ëèíèþ, ïàðàëëåëüíóþ îñè òîêîâ (ðèñ.1.1).
Ðèñ. 1.1
Íåçàâèñèìûì èñòî÷íèêîì òîêà íàçûâàþò äâóõïîëþñíèê, òîê ÷åðåç
âûõîäíûå çàæèìû êîòîðîãî çàäàí äëÿ êàæäîãî ìîìåíòà âðåìåíè, è íå çàâèñèò
îò íàïðÿæåíèÿ íà åãî çàæèìàõ. Òîê òàêîãî èñòî÷íèêà ìîæåò ïðîèçâîëüíî
èçìåíÿòüñÿ âî âðåìåíè.  ÷àñòíîì ñëó÷àå, êîãäà òîê íå çàâèñèò îò âðåìåíè,
òàêîé èñòî÷íèê íàçûâàþò èñòî÷íèêîì ïîñòîÿííîãî òîêà.
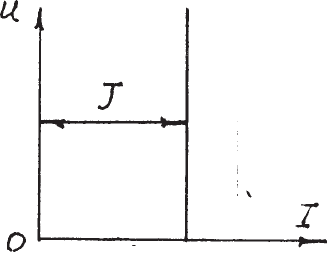
Îñíîâíîé õàðàêòåðèñòèêîé ýòîãî èñòî÷íèêà ÿâëÿåòñÿ âíåøíÿÿ
õàðàêòåðèñòèêà çàâèñèìîñòü íàïðÿæåíèÿ íà åãî çàæèìàõ îò òîêà èñòî÷íèêà.
Äëÿ èñòî÷íèêà ïîñòîÿííîãî òîêà âíåøíÿÿ õàðàêòåðèñòèêà ïðåäñòàâëÿåò ñîáîé
ïðÿìóþ ëèíèþ, ïàðàëëåëüíóþ îñè íàïðÿæåíèÿ (ðèñ.1.2).
12
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
Ðèñ. 1.2
 îòëè÷èå îò íåçàâèñèìûõ èñòî÷íèêîâ ýíåðãèè, çàâèñèìûå èñòî÷íèêè
èìåþò íå îäíó ïàðó çàæèìîâ, à äâå: âûõîäíóþ è óïðàâëÿþùóþ. Çàâèñèìûå
èñòî÷íèêè ÿâëÿþòñÿ ÷åòûðåõïîëþñíèêàìè.
Çàâèñèìûìè èñòî÷íèêàìè ÝÄÑ íàçûâàþò èñòî÷íèêè, ýëåêòðîäâèæóùàÿ
ñèëà êîòîðûõ çàâèñèò ëèáî îò òîêà, ëèáî îò íàïðÿæåíèÿ íà íåêîòîðîì ó÷àñòêå
öåïè.
 îáùåì ñëó÷àå ñâÿçü ìåæäó óïðàâëÿþùåé è âûõîäíîé âåëè÷èíàìè â
êàæäîì èñòî÷íèêå ìîæåò áûòü ñëîæíîé, íî äëÿ ðåøåíèÿ çàäà÷ òåîðèè öåïåé
äîñòàòî÷íî çàâèñèìûõ èñòî÷íèêîâ, ó êîòîðûõ óïðàâëÿþùèå è âûõîäíûå
íàïðÿæåíèÿ èëè òîêè ñâÿçàíû ëèíåéíûìè çàâèñèìîñòÿìè.  òàêèõ èñòî÷íèêàõ
âûõîäíîé ïàðàìåòð Y ïðÿìîïðîïîðöèîíàëåí óïðàâëÿþùåìó âîçäåéñòâèþ:
Y=kõ.
Êîýôôèöèåíò ïðîïîðöèîíàëüíîñòè k íàçûâàåòñÿ êîýôôèöèåíòîì
óïðàâëåíèÿ, êîòîðûé â çàâèñèìîñòè îò òèïà èñòî÷íèêà ìîæåò èìåòü
ðàçìåðíîñòü ñîïðîòèâëåíèÿ, ïðîâîäèìîñòè èëè áûòü áåçðàçìåðíîé âåëè÷èíîé.
Åñëè óïðàâëÿþùèå âîçäåéñòâèÿ òàêèõ çàâèñèìûõ èñòî÷íèêîâ ðàâíû íóëþ, òî
íà èõ âûõîäå áóäóò ðàâíû íóëþ ñîîòâåòñòâåííî ÝÄÑ èëè òîêè.
Êàæäûé àêòèâíûé ýëåìåíò õàðàêòåðèçóåòñÿ òîëüêî îäíèì ïàðàìåòðîì
ÝÄÑ èëè òîêîì íà âûõîäíûõ çàæèìàõ èñòî÷íèêîâ.
Ñ ïîìîùüþ àêòèâíûõ è ïàññèâíûõ ñõåìíûõ ýëåìåíòîâ ìîæíî
ïðîìîäåëèðîâàòü ëþáîé ýëåìåíò ýëåêòðè÷åñêîé öåïè, ïðåäñòàâèâ åãî â âèäå
ñõåìû çàìåùåíèÿ.
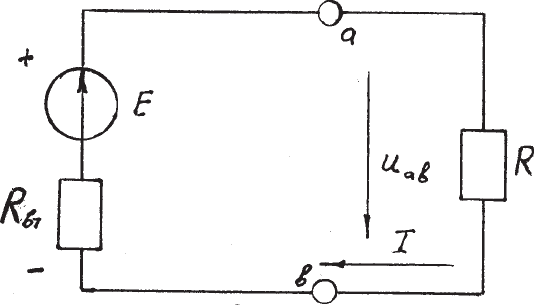
Íà ðèñ.1.3 ïðèâåäåíà ñõåìà çàìåùåíèÿ äëÿ ïðîñòåéøåé ýëåêòðè÷åñêîé
öåïè ïîñòîÿííîãî òîêà, ñîñòîÿùàÿ èç èñòî÷íèêà ïèòàíèÿ è ïðèåìíèêà
(ïîòðåáèòåëÿ). Èñòî÷íèê ïèòàíèÿ íà ðèñóíêå 1.3 ïðåäñòàâëåí â âèäå äâóõ
ýëåìåíòîâ. Îäèí èç íèõ, Å, óêàçûâàåò, ÷òî â èñòî÷íèêå åñòü ÝÄÑ Å, ñòðåëêà
ïîêàçûâàåò íàïðàâëåíèå ÝÄÑ ñèëû, äåéñòâóþùåé íà ïîëîæèòåëüíûå çàðÿäû.
Âòîðîé ñîïðîòèâëåíèå R
âò
, îïðåäåëÿåò ïðåîáðàçîâàíèå ýëåêòðè÷åñêîé
ýíåðãèè â òåïëîâóþ âíóòðè èñòî÷íèêà.  ïîòðåáèòåëå ïðîèñõîäèò
ïðåîáðàçîâàíèå ýëåêòðè÷åñêîé ýíåðãèè â äðóãèå âèäû: ìåõàíè÷åñêóþ,
òåïëîâóþ è ò.ä. Äëÿ ïðèåìíèêà çàäàåòñÿ åãî ñîïðîòèâëåíèå R. Òîê ïðîòåêàåò
ïî çàìêíóòîìó êîíòóðó, ñîñòîÿùåìó èç èñòî÷íèêà è ïðèåìíèêà, â ïðèåìíèêå
îò âûâîäà à ê âûâîäó â. Â ïðîñòåéøåé ñõåìå íå ó÷òåíî ñîïðîòèâëåíèå
13
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
ïðîâîäîâ, ò.ê. ÷àñòî èõ ñîïðîòèâëåíèå ìíîãî ìåíüøå ñîïðîòèâëåíèÿ
ïîòðåáèòåëÿ.
Ðèñ. 1.3
1.1.4. Ïîñòîÿííûé ýëåêòðè÷åñêèé òîê
Äëÿ âîçíèêíîâåíèÿ è ïðîõîæäåíèÿ ýëåêòðè÷åñêîãî òîêà â ïðîâîäíèêå
íåîáõîäèìû íîñèòåëè çàðÿäîâ (èîíû è ñâîáîäíûå ýëåêòðîíû) è ýëåêòðè÷åñêîå
ïîëå â ýòîì ïðîâîäíèêå. Ïîëå â ïðîâîäíèêå ñîçäàåòñÿ çàðÿäàìè,
íàêàïëèâàþùèìèñÿ íà ýëåêòðîäàõ èñòî÷íèêà ïîä äåéñòâèåì ìåõàíè÷åñêèõ,
õèìè÷åñêèõ èëè èíûõ ñèë, äåéñòâóþùèõ â èñòî÷íèêå. Ýëåêòðè÷åñêèé òîê
ïðîõîäèò ÷åðåç ïðîâîäíèê, åñëè èñòî÷íèê ýëåêòðè÷åñêîé ýíåðãèè âìåñòå ñ
ïðîâîäíèêîì îáðàçóþò õîòÿ áû ïðîñòåéøóþ ýëåêòðè÷åñêóþ öåïü.
Ýëåêòðè÷åñêîå ïîëå â ïðîâîäíèêå íàçûâàåòñÿ ñòàöèîíàðíûì
ýëåêòðè÷åñêèì ïîëåì, åñëè òîê â ïðîâîäíèêå ñ òå÷åíèåì âðåìåíè íå
èçìåíÿåòñÿ. Ñòàöèîíàðíîå ïîëå â ïðîâîäíèêå õàðàêòåðèçóåòñÿ
íàïðÿæåííîñòüþ ýëåêòðè÷åñêîãî ïîëÿ ε, êîòîðàÿ íå èçìåíÿåòñÿ ñ òå÷åíèåì
âðåìåíè.
Åñëè ïðèëîæèòü ýëåêòðè÷åñêîå íàïðÿæåíèå ê äâóì ìåòàëëè÷åñêèì
ýëåêòðîäàì, ïîãðóæåííûì â ýëåêòðîëèò, òî ïîä äåéñòâèåì ýëåêòðè÷åñêîãî
ïîëÿ ïîëîæèòåëüíî çàðÿæåííûå èîíû áóäóò äâèãàòüñÿ ê îòðèöàòåëüíî
çàðÿæåííîìó ýëåêòðîäó (êàòîäó), à îòðèöàòåëüíî çàðÿæåííûå èîíû ê
ïîëîæèòåëüíîìó ýëåêòðîäó (àíîäó). Âñòðå÷íûå, ïðîòèâîïîëîæíî çàðÿæåííûå
ïîòîêè èîíîâ ïðåäñòàâëÿþò ñîáîé ýëåêòðè÷åñêèé òîê. Îòðèöàòåëüíûå èîíû
îòäàþò àíîäó ýëåêòðîíû, êîòîðûå ïðîäîëæàþò äâèãàòüñÿ ê èñòî÷íèêó.
Ïîëîæèòåëüíûå èîíû ñîåäèíÿþòñÿ ñî ñâîáîäíûìè ýëåêòðîíàìè êàòîäà,
ïðèõîäÿùèìè îò èñòî÷íèêà. Íàïðàâëåíèå òîêà I â ïðîâîäíèêå ñ÷èòàþò
ñîâïàäàþùèì ñ íàïðàâëåíèåì íàïðÿæåííîñòè ïîëÿ è íàïðàâëåíèåì äâèæåíèÿ
ïîëîæèòåëüíûõ çàðÿäîâ èëè íàïðàâëåíèå, îáðàòíîå íàïðàâëåíèþ äâèæåíèÿ
ýëåêòðîíîâ.
Íå èçìåíÿþùèéñÿ âî âðåìåíè òîê I íàçûâàåòñÿ ïîñòîÿííûì
ýëåêòðè÷åñêèì òîêîì. Ïîñòîÿííûé òîê èëè ñèëà òîêà I îïðåäåëÿåòñÿ
êîëè÷åñòâîì ýëåêòðè÷åñòâà, ïðîõîäÿùèì ÷åðåç ïîïåðå÷íîå ñå÷åíèå
ïðîâîäíèêà çà åäèíèöó âðåìåíè.
Åñëè îáîçíà÷èòü çàðÿä, ïðîõîäÿùèé ÷åðåç ïîïåðå÷íîå ñå÷åíèå
ïðîâîäíèêà çà âðåìÿ t, êàê Q, òî ñèëó òîêà ìîæíî îïðåäåëèòü êàê:
14
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
I = Q / t. (1.4)
Åäèíèöåé ñèëû òîêà ÿâëÿåòñÿ Àìïåð (À). Ïîñòîÿííûé òîê â ïðîâîäíèêå
ðàâåí îäíîìó Àìïåðó, åñëè ÷åðåç ïîïåðå÷íîå ñå÷åíèå çà 1 ñåêóíäó ïðîõîäèò
ýëåêòðè÷åñêèé çàðÿä, ðàâíûé îäíîìó Êóëîíó (1 Êë).
1.1.5. Ïîñëåäîâàòåëüíîå ñîåäèíåíèå ýëåìåíòîâ
ýëåêòðè÷åñêîé öåïè
Àíàëèç ëþáîé ýëåêòðè÷åñêîé öåïè íà÷èíàåòñÿ ñ ïîñòðîåíèÿ åå ìîäåëè,
êîòîðàÿ îïèñûâàåòñÿ ñõåìîé çàìåùåíèÿ.  îáùåì ñëó÷àå òàêèå ñõåìû
ñîäåðæàò âñå òðè òèïà ïàññèâíûõ ñõåìíûõ ýëåìåíòîâ: ðåçèñòèâíûå,
èíäóêòèâíûå è åìêîñòíûå. Ïðè ïîñòîÿííîì òîêå ñîïðîòèâëåíèå èíäóêòèâíîãî
ýëåìåíòà ðàâíî íóëþ. Ñîïðîòèâëåíèå åìêîñòíîãî ýëåìåíòà ðàâíî
áåñêîíå÷íîñòè. Ïðè ïîñòîÿííîì òîêå ñõåìû çàìåùåíèÿ ïðåäñòàâëÿþò ñîáîé
ñîåäèíåíèÿ òîëüêî ðåçèñòèâíûõ ýëåìåíòîâ ñ èñòî÷íèêàìè ïîñòîÿííûõ òîêîâ
è ÝÄÑ. Òàêèå ñõåìû íàçûâàþò ðåçèñòèâíûìè. Íàèáîëåå ïðîñòûìè ÿâëÿþòñÿ
ëèíåéíûå ðåçèñòèâíûå ñõåìû, â êîòîðûõ ñîïðîòèâëåíèå êàæäîãî ðåçèñòèâíîãî
ýëåìåíòà ïîñòîÿííî.
Åñëè íåñêîëüêî ðåçèñòîðîâ ñîåäèíåíû îäèí çà äðóãèì áåç ðàçâåòâëåíèé
è ïî íèì ïðîõîäèò îäèí è òîò æå òîê, òî îíè îáðàçóþò îäíó âåòâü, è òàêîå
ñîåäèíåíèå ðåçèñòîðîâ íàçûâàåòñÿ ïîñëåäîâàòåëüíûì.
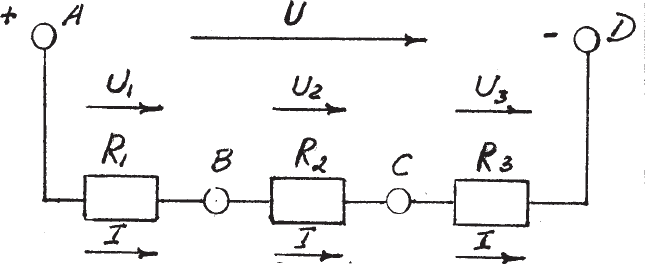
Ïðèìåðîì ñõåìû, ñîñòîÿùåé èç ïîñëåäîâàòåëüíî ñîåäèíåííûõ
ðåçèñòèâíûõ ýëåìåíòîâ R
1
, R
2
, R
3
, ÿâëÿåòñÿ ñõåìà, ïðåäñòàâëåííàÿ íà ðèñ.1.4.
Ðèñ.1.4
Ñîãëàñíî çàêîíó Îìà, íàïðÿæåíèÿ íà ðåçèñòîðàõ èëè ïàäåíèÿ íàïðÿæåíèÿ
îïðåäåëÿþòñÿ âûðàæåíèÿìè:
U
1
= R
1
I; U
2
= R
2
I; U
3
= R
3
I;
èç ÷åãî ñëåäóåò U
1
: U
2
: U
3
= R
1
: R
2
: R
3
. Òàêèì îáðàçîì, ïàäåíèÿ íàïðÿæåíèÿ
íà ïîñëåäîâàòåëüíî ñîåäèíåííûõ ðåçèñòîðàõ ïðîïîðöèîíàëüíû çíà÷åíèÿì
èõ ñîïðîòèâëåíèé. Íàïðÿæåíèÿ íà ðåçèñòîðàõ ìîæíî âûðàçèòü ÷åðåç ðàçíîñòü
ïîòåíöèàëîâ íà èõ âûâîäàõ:
U
1
=ϕ
À
- ϕ
Â
; U
2
= ϕ
Â
- ϕ
Ñ
; U
3
= ϕ
Ñ
- ϕ
D
.
15
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
Èç ýòîãî ñëåäóåò:
U
1
+ U
2
+ U
3
= ϕ
À
+ ϕ
Â
- ϕ
Â
- ϕ
Ñ
+ ϕ
Ñ
- ϕ
D
=ϕ
À
-ϕ
D
=U. (1.5)
Ñóììà ïàäåíèé íàïðÿæåíèé íà ïîñëåäîâàòåëüíî ñîåäèíåííûõ ðåçèñòîðàõ
ðàâíà íàïðÿæåíèþ íà âûâîäàõ âñåãî ó÷àñòêà öåïè.
Ðÿä ïîñëåäîâàòåëüíî ñîåäèíåííûõ ðåçèñòîðîâ ìîæíî çàìåíèòü
ýêâèâàëåíòíûì ñîïðîòèâëåíèåì. Åñëè ïîìíîæèòü óðàâíåíèå (1.5) íà 1 / I, òî
ïîëó÷èì:
R.RRR
I
U
I
UUU
321
321
=++==
++
(1.6)
Èç óðàâíåíèÿ (1.6) ñëåäóåò, ÷òî ýêâèâàëåíòíîå ñîïðîòèâëåíèå
ïîñëåäîâàòåëüíî ñîåäèíåííûõ ðåçèñòîðîâ ðàâíî ñóììå èõ ñîïðîòèâëåíèé.
1.1.6. Ïàðàëëåëüíîå ñîåäèíåíèå ýëåìåíòîâ
ýëåêòðè÷åñêîé öåïè
Ïàðàëëåëüíûì ñîåäèíåíèåì ðåçèñòîðîâ, âåòâåé íàçûâàåòñÿ òàêîå
ñîåäèíåíèå, ïðè êîòîðîì ê îäíèì è òåì æå äâóì óçëàì ýëåêòðè÷åñêîé öåïè
ïðèñîåäèíåíû íåñêîëüêî ðåçèñòîðîâ, âåòâåé. Ïðè ïàðàëëåëüíîì ñîåäèíåíèè
ýëåìåíòîâ ýëåêòðè÷åñêîé öåïè íà âñåõ ó÷àñòêàõ òàêîé öåïè íàïðÿæåíèå îäíî
è òî æå.
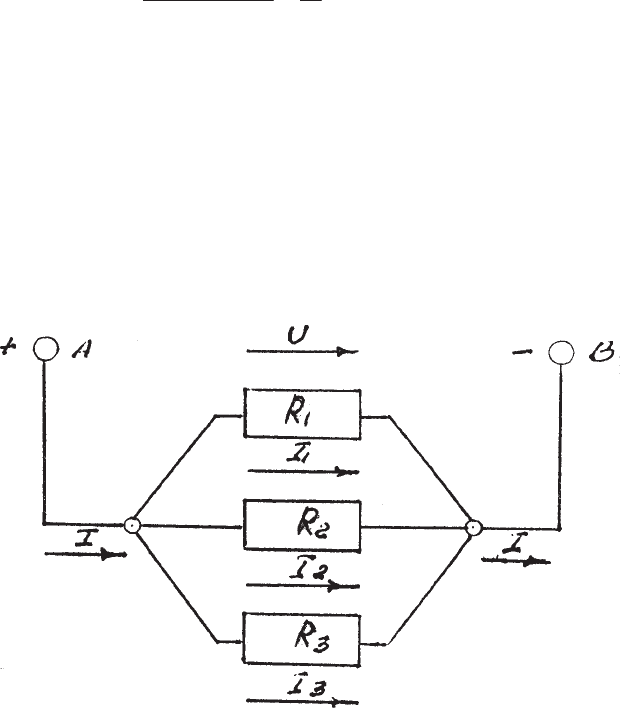
Ïðèìåðîì ñõåìû, ñîñòîÿùåé èç ïàðàëëåëüíî ñîåäèíåííûõ ðåçèñòèâíûõ
ýëåìåíòîâ R1, R2, R3, ñëóæèò ñõåìà, ïðèâåäåííàÿ íà ðèñ.1.5.
Ðèñ. 1.5

16
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
Ñîãëàñíî çàêîíó Îìà, òîêè â ðåçèñòîðàõ îïðåäåëÿþòñÿ ïî ôîðìóëàì:
I
1
= U / R
1
; I
2
= U / R
2
; I
3
= U / R
3
.
Èç ýòèõ ôîðìóë ñëåäóåò, ÷òî:
I
1
/ I
2
/ I
3
=
321
R
1
:
R
1
:
R
1
. (1.7)
Ñîãëàñíî ôîðìóëå (1.7), òîêè â ïàðàëëåëüíûõ âåòâÿõ ñ ðåçèñòîðàìè
îáðàòíî ïðîïîðöèîíàëüíû èõ ñîïðîòèâëåíèÿì.
Ðÿä ïàðàëëåëüíî ñîåäèíåííûõ ðåçèñòîðîâ ìîæíî çàìåíèòü
ýêâèâàëåíòíûì ñîïðîòèâëåíèåì R, çíà÷åíèå êîòîðîãî äîëæíî áûòü òàêèì,
÷òîáû ïðè òîì æå íàïðÿæåíèè íà âûâîäàõ òîê â ýêâèâàëåíòíîì ðåçèñòîðå
áûë ðàâåí ñóììå òîêîâ â îòäåëüíûõ âåòâÿõ:
321
III
U
I
U
R
++
==
.
Ýêâèâàëåíòíàÿ ïðîâîäèìîñòü:
321
321
R
1
R
1
R
1
U
III
R
1
++=
++
=
. (1.8)
Ýêâèâàëåíòíàÿ ïðîâîäèìîñòü ïàðàëëåëüíîãî ñîåäèíåíèÿ ðåçèñòîðîâ
ðàâíà ñóììå ïðîâîäèìîñòåé âñåõ ïàðàëëåëüíûõ âåòâåé. Ýêâèâàëåíòíîå
ñîïðîòèâëåíèå ìåíüøå ñàìîãî ìàëîãî èç ïàðàëëåëüíî ñîåäèíåííûõ
ñîïðîòèâëåíèé. Ïðè òðåõ âåòâÿõ ýêâèâàëåíòíàÿ ïðîâîäèìîñòü ðàâíà:
.
321
323121
321
RRR
RRRRRR
R
1
R
1
R
1
R
1
++
=++=
Ýêâèâàëåíòíîå ñîïðîòèâëåíèå ïàðàëëåëüíîãî ñîåäèíåíèÿ ðåçèñòîðîâ
ðàâíî:
.
323121
321
RRRRRR
RRR
R
++
=
(1.9)

17
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
1.1.7. Ðåçèñòîð
Ýëåìåíòû, âêëþ÷åííûå â ýëåêòðè÷åñêóþ öåïü äëÿ îãðàíè÷åíèÿ èëè
ðåãóëèðîâàíèÿ òîêà, íàçûâàþòñÿ ðåçèñòîðàìè. Ðåçèñòîðû áûâàþò
ïðîâîëî÷íûå è íåïðîâîëî÷íûå, ðåãóëèðóåìûå è íåðåãóëèðóåìûå. Â
ïðîâîëî÷íûõ ðåçèñòîðàõ òîêîïðîâîäÿùèì ìàòåðèàëîì ñëóæèò ìåòàëëè÷åñêàÿ
ïðîâîëîêà èç ñïëàâîâ ñ âûñîêèì óäåëüíûì ýëåêòðè÷åñêèì ñîïðîòèâëåíèåì,
à â íåïðîâîëî÷íûõ ñëîé èëè ñòåðæåíü èç ìàòåðèàëà ñ âûñîêèì óäåëüíûì
ñîïðîòèâëåíèåì. Ðåãóëèðóåìûé ïðîâîëî÷íûé ðåçèñòîð íàçûâàåòñÿ ðåîñòàòîì.
Îáìîòêè ðåîñòàòîâ èçãîòàâëèâàþòñÿ èç ñïëàâîâ ñ áîëüøèì óäåëüíûì
ñîïðîòèâëåíèåì, ÷òî äàåò âîçìîæíîñòü ïðè ìàëîé äëèíå ïîëó÷èòü
íåîáõîäèìîå ñîïðîòèâëåíèå. Îäèí çàæèì ðåîñòàòà ñîåäèíåí ñ ïîäâèæíûì
êîíòàêòîì, à äâà äðóãèõ ñ êîíöàìè ñïèðàëè. Ïåðåìåùàÿ ïîäâèæíûé êîíòàêò,
ìîæíî èçìåíÿòü ñîïðîòèâëåíèå ìåæäó âûâîäàìè. Ïðè ìàëûõ òîêàõ ïðèìåíÿþò
íåïðîâîëî÷íûå ïåðåìåííûå ðåçèñòîðû.
1.1.8. Èíäóêòèâíàÿ êàòóøêà (êàòóøêà èíäóêòèâíîñòè)
Âîêðóã çàìêíóòîãî êîíòóðà ñ òîêîì âñåãäà ñóùåñòâóåò ìàãíèòíûé ïîòîê,
ïðîíèçûâàþùèé êîíòóð. Ýòîò ìàãíèòíûé ïîòîê íàçûâàåòñÿ ìàãíèòíûì ïîòîêîì
ñàìîèíäóêöèè.
Àëãåáðàè÷åñêàÿ ñóììà ïîòîêîâ ñàìîèíäóêöèè âñåõ âèòêîâ îáìîòêè êàòóøêè
íàçûâàåòñÿ ïîòîêîñöåïëåíèåì ñàìîèíäóêöèè. Êîýôôèöèåíò ïðîïîðöèîíàëü-
íîñòè ìåæäó ïîòîêîñöåïëåíèåì ñàìîèíäóêöèè è ïîòîêîì I êàòóøêè íàçûâàåòñÿ
èíäóêòèâíîñòüþ:
L = ψ / I. (1.10)
Èíäóêòèâíîñòü õàðàêòåðèçóåò ñâÿçü ïîòîêîñöåïëåíèÿ ñàìîèíäóêöèè ñ
òîêîì äàííîé öåïè.
Åäèíèöà èçìåðåíèÿ èíäóêòèâíîñòè : Îì çà ñåêóíäó (Îì⋅ñ).
Åäèíèöà Îì⋅ñ íàçûâàåòñÿ Ãåíðè (Ãí). Ïðîèçâåäåíèå ÷èñëà âèòêîâ ω íà
çíà÷åíèå ìàãíèòíîãî ïîòîêà φ îïðåäåëÿåò ïîòîêîñöåïëåíèå êàòóøêè:
ψ = ω⋅φ.
 ñâîþ î÷åðåäü, ìàãíèòíûé ïîòîê φ îïðåäåëÿåòñÿ ïî ôîðìóëå:
φ = Â⋅ S, (1.11)
ãäå  ìàãíèòíàÿ èíäóêöèÿ; S ïëîñêàÿ ïëîùàäêà, âî âñåõ òî÷êàõ
êîòîðîé ïåðïåíäèêóëÿðíûå ê íåé âåêòîðû èíäóêöèè ÷èñëåííî ðàâíû ìåæäó
ñîáîé.
Ìàãíèòíàÿ èíäóêöèÿ îïðåäåëÿåòñÿ ïî ôîðìóëå:
r2
I
B
a
π
µ=
(1.12)
ãäå µ
a
- àáñîëþòíàÿ ìàãíèòíàÿ ïðîíèöàåìîñòü, ó÷èòûâàþùàÿ âëèÿíèå
ñðåäû, â êîòîðîé íàõîäèòñÿ ïðîâîä.
Ìàãíèòíàÿ èíäóêöèÿ âíóòðè ìàãíèòîïðîâîäà â ëþáîé òî÷êå îêðóæíîñòè
ðàäèóñà r ðàâíà:

18
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
,
8
r
10
I
ù
125
ì
B
−
=
l
(1.13)
ãäå I ñèëà òîêà (À);
l
äëèíà êîíòóðà (Ì); µ
r
- îòíîñèòåëüíàÿ ìàãíèòíàÿ
ïðîíèöàåìîñòü.
Ïðè ýëåêòðîòåõíè÷åñêèõ ðàñ÷åòàõ îòíîñèòåëüíàÿ ìàãíèòíàÿ
ïðîíèöàåìîñòü äëÿ ìàòåðèàëîâ, êðîìå ôåððîìàãíèòíûõ, ïðèíèìàåòñÿ ðàâíîé
åäèíèöå. Ê ôåððîìàãíèòíûì ìàòåðèàëàì îòíîñÿòñÿ: òåõíè÷åñêîå æåëåçî,
íèçêîóãëåðîäèñòûå ñòàëè, æåëåçîíèêåëåâûå ñïëàâû, ñïëàâû æåëåçà ñ íèêåëåì,
ìîëèáäåíîì, õðîìîì, êðåìíèåì, ôåððîìàãíèòíûå ìàòåðèàëû, ïîëó÷åííûå
èç ñìåñè îêèñëîâ æåëåçà è öèíêà; óãëåðîäèñòûå, âîëüôðàìîâûå, õðîìèñòûå
è êîáàëüòîâûå ñòàëè. Ó ôåððèòíûõ ìàòåðèàëîâ îòíîñèòåëüíàÿ ìàãíèòíàÿ
ïðîíèöàåìîñòü ìîæåò äîñòèãàòü äåñÿòêîâ òûñÿ÷ è çàâèñèò îò èíòåíñèâíîñòè
ìàãíèòíîãî ïîëÿ.
Èñõîäÿ èç ôîðìóë (1.10), (1.11), (1.12), íàõîäèì:
L = ψ / I = ω⋅φ / I = ω ⋅ Â⋅ S / I = 125 µ
r
.
8
10
S
ùù
−
⋅⋅
l
(1.14)
1.1.9. Êîíäåíñàòîð
Ñèñòåìà èç äâóõ ìåòàëëè÷åñêèõ ïëàñòèí ïðîèçâîëüíîé ôîðìû,
ðàçäåëåííûõ äèýëåêòðèêîì, îáðàçóþò êîíäåíñàòîð. Êîíäåíñàòîðû îáëàäàþò
ñâîéñòâîì íàêàïëèâàòü è óäåðæèâàòü íà ñâîèõ ïëàñòèíàõ ðàâíûå ïî çíà÷åíèþ
è ðàçíûå ïî çíàêó ýëåêòðè÷åñêèå çàðÿäû +Q è Q.
Åìêîñòüþ êîíäåíñàòîðà íàçûâàåòñÿ êîýôôèöèåíò ïðîïîðöèîíàëüíîñòè
ìåæäó çàðÿäîì Q è íàïðÿæåíèåì U ìåæäó ïëàñòèíàìè êîíäåíñàòîðà:
Ñ = Q / U. (1.15)
Åäèíèöåé èçìåðåíèÿ åìêîñòè ñëóæèò ôàðàä (Ô) åìêîñòü êîíäåíñàòîðà,
çàðÿä êîòîðîãî ðàâåí îäíîìó Êóëîíó ïðè íàïðÿæåíèè íà ïëàñòèíàõ, ðàâíîìó
îäíîìó Âîëüòó.
Êîíäåíñàòîðû ìîãóò ñîåäèíÿòüñÿ ïîñëåäîâàòåëüíî è ïàðàëëåëüíî.
 ñëó÷àå n îäèíàêîâûõ, ïîñëåäîâàòåëüíî ñîåäèíåííûõ êîíäåíñàòîðîâ
åìêîñòüþ Ñ êàæäûé îáùàÿ åìêîñòü êîíäåíñàòîðîâ ðàâíà:
Ñ
Σ
= Ñ / n. (1.16)
Ïðè n îäèíàêîâûõ ïàðàëëåëüíî ñîåäèíåííûõ êîíäåíñàòîðàõ îáùàÿ
åìêîñòü ðàâíà:
Ñ
Σ
= Ñ ⋅ n. (1.17)
1.1.10. Âîëüò-àìïåðíàÿ õàðàêòåðèñòèêà
Çàâèñèìîñòü íàïðÿæåíèÿ îò ñèëû òîêà U(I) èëè ñèëû òîêà îò íàïðÿæåíèÿ
I(U) íàçûâàåòñÿ âîëüò-àìïåðíîé õàðàêòåðèñòèêîé.
Äëÿ ïðèåìíèêà ñ ñîïðîòèâëåíèåì R âîëüò-àìïåðíàÿ õàðàêòåðèñòèêà
ïðåäñòàâëåíà íà ðèñ.1.6.

19
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
Ðèñ.1.6
Ïî çàäàííîé âîëüò-àìïåðíîé õàðàêòåðèñòèêå ìîæíî îïðåäåëèòü
ñîïðîòèâëåíèå ïðèåìíèêà, âûáðàâ îäíó èç òî÷åê ýòîé õàðàêòåðèñòèêè.
Íàïðèìåð:
R = U
ïð
/ I
ïð.
Åñëè ñîïðîòèâëåíèå ýëåìåíòà ïîñòîÿííî, òî ýëåìåíò íàçûâàåòñÿ
ëèíåéíûì, íî, ñòðîãî ãîâîðÿ, ëèíåéíûõ ýëåìåíòîâ íåò, ò.ê. ïðè ðàçëè÷íûõ
òîêàõ â ïðîâîäíèêå èçìåíÿåòñÿ åãî òåìïåðàòóðà è, ñëåäîâàòåëüíî,
ñîïðîòèâëåíèå. Ëþáîé ýëåìåíò öåïè íåëèíååí. Îäíàêî, åñëè íåëèíåéíîñòü
íåâåëèêà, òî ýëåìåíò ïðàêòè÷åñêè ìîæíî ñ÷èòàòü ëèíåéíûì. Ýëåêòðè÷åñêàÿ
öåïü íàçûâàåòñÿ ëèíåéíîé, åñëè îíà ñîäåðæèò òîëüêî ëèíåéíûå ýëåìåíòû.
Öåïü íåëèíåéíà, åñëè â íåé ïðèñóòñòâóåò îäèí èëè íåñêîëüêî íåëèíåéíûõ
ýëåìåíòîâ. Ó ëèíåéíîãî ýëåìåíòà âîëüò-àìïåðíàÿ õàðàêòåðèñòèêà ïðåäñòàâëÿåò
ñîáîé ïðÿìóþ, ïðîõîäÿùóþ ÷åðåç íà÷àëî êîîðäèíàò (ðèñ.1.6). Äëÿ íåëèíåéíîãî
ýëåìåíòà îíà íåïðÿìîëèíåéíà. Íàïðèìåð, âîëüò-àìïåðíàÿ õàðàêòåðèñòèêà
ëàìïû ñ ìåòàëëè÷åñêîé íèòüþ îòëè÷àåòñÿ îò ïðÿìîé, îòêëîíÿÿñü âíèç
(ðèñ.1.7).
Ðèñ.1.7
Îáû÷íî õàðàêòåðèñòèêè íåëèíåéíûõ ýëåìåíòîâ çàäàþòñÿ â âèäå òàáëèö
èëè ãðàôèêîâ.
20
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
1.1.11. Âíåøíÿÿ õàðàêòåðèñòèêà èñòî÷íèêà
ýëåêòðè÷åñêîé ýíåðãèè
Ñõåìû çàìåùåíèÿ èñòî÷íèêîâ ýíåðãèè ñòðîÿò íà îñíîâå èõ âíåøíèõ
õàðàêòåðèñòèê çàâèñèìîñòåé âûõîäíîãî íàïðÿæåíèÿ èñòî÷íèêîâ îò
âåëè÷èíû îòäàâàåìîãî èìè òîêà U = F ( I ).
Çàâèñèìîñòü âûõîäíîãî íàïðÿæåíèÿ îò âåëè÷èíû îòäàâàåìîãî òîêà
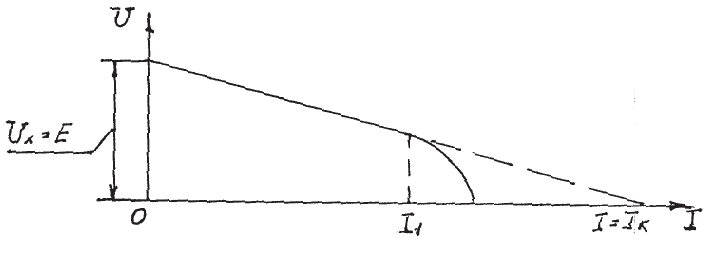
ïðèâåäåíà íà ðèñ.1.8.
Ðèñ.1.8
Êàê ñëåäóåò èç ðèñ.1.8, ïðè óâåëè÷åíèè òîêà, îòäàâàåìîãî èñòî÷íèêîì
ýíåðãèè, íàïðÿæåíèå U íà åãî çàæèìàõ óìåíüøàåòñÿ. Ïðè çíà÷åíèÿõ òîêà îò
íóëÿ äî íåêîòîðîãî çíà÷åíèÿ I = I
1
, íàïðÿæåíèå ïàäàåò ïî çàêîíó, áëèçêîìó ê
ëèíåéíîìó, çàòåì ëèíåéíàÿ çàâèñèìîñòü ìåæäó U è I íàðóøàåòñÿ, è
íàïðÿæåíèå íà÷èíàåò ðåçêî ïàäàòü. Äëÿ áîëüøèíñòâà ïðàêòè÷åñêè âàæíûõ
ñëó÷àåâ äîñòàòî÷íî ïðîìîäåëèðîâàòü ðàáî÷èé ó÷àñòîê âíåøíåé õàðàêòåðèñòèêè
èñòî÷íèêà ýíåðãèè, êîòîðûì ÿâëÿåòñÿ ó÷àñòîê 0< I < I
1
, ãäå íàïðÿæåíèå è
òîê ñâÿçàíû çàâèñèìîñòüþ, áëèçêîé ê ëèíåéíîé.
Äëÿ ðàáî÷åãî ó÷àñòêà âíåøíþþ õàðàêòåðèñòèêó èñòî÷íèêà ýíåðãèè ìîæíî
àïïðîêñèìèðîâàòü ïðÿìîé ëèíèåé. Óðàâíåíèå ïðÿìîé â îòðåçêàõ äëÿ êîîðäèíàò
U, I çàïèñûâàåòñÿ â âèäå:
I / I
ê
+ U / U
x
= 1, (1.18)
ãäå I
ê
òîê êîðîòêîãî çàìûêàíèÿ; U
õ
íàïðÿæåíèå õîëîñòîãî õîäà (I
x
=0).
Èç ôîðìóëû (1.18) ñëåäóåò:
U = U
x
(U
x
/ I
ê
) I èëè
U = U
x
R
âò
I , (1.19)
ãäå R
âò
= U
x
/ I
ê
- âíóòðåííåå ñîïðîòèâëåíèå èñòî÷íèêà ýíåðãèè.
Óðàâíåíèå (1.18) ìîæíî ïåðåïèñàòü â âèäå:
I = I
ê
G
âò
U , (1.20)
ãäå G
âò
= 1 / R
âò
âíóòðåííÿÿ ïðîâîäèìîñòü èñòî÷íèêà ýíåðãèè.
Óðàâíåíèþ (1.19) ñîîòâåòñòâóåò ñõåìà çàìåùåíèÿ, íàçûâàåìàÿ ñõåìîé ñ
èñòî÷íèêîì ÝÄÑ, à óðàâíåíèå (1.20) ñõåìà ñ èñòî÷íèêîì ïèòàíèÿ.
