Egerton R.F. Electron Energy-Loss Spectroscopy in the Electron Microscope

Подождите немного. Документ загружается.

408 Appendix B: Computer Programs

noise statistics. For an electron-counting system, fpoiss = cpe = 1; otherwise the

value may be greater or less than 1, depending on the sensitivity of the scintillator.

Background noise (bnoise), which might represent electronic noise of the electron

detector, is taken as the background level multiplied by a factor fback. Stochastic

numbers rndnum (mean amplitude = 1) are generated as rounding errors of arbi-

trary real numbers rlnum and are not truly random; they repeat exactly each time the

program is run (not necessarily a disadvantage). Setting cpe =0 = fback provides a

noise-free s pectrum.

Input is of the form: SpecGen(ep,wp,wz,tol,a0,ez,epc,nd,back,fback,cpe). The

output ﬁles are also plotted.

B.5 Fourier-Log Deconvolution

The program FLOG calculates a single scattering distribution based on Eqs. (4.10)

and (4.11). Input is of the form F

LOG(inﬁle,fwhm2). PSD data generated by

PECGEN can be used as a test inﬁle.

Data values are read from the chosen two-column inﬁle, assumed to consist of

pairs of ﬂoating point numbers representing energy loss and spectral intensity. The

instrumental background level back is estimated from the ﬁrst ﬁve intensity (y)

values; if these points are not representative, background subtraction should be per-

formed manually before using F

LOG. The eV/channel value epc is obtained from

the ﬁrst and ﬁfth energy (x) values; the zero-loss channel number nz is found by

detecting the ﬁrst y-value maximum. The separation point nsep between the elastic

and inelastic data is taken as the subsequent minimum in J(E)/E; the 1/E weighting

helps to discriminate against glitches on the zero-loss proﬁle. The zero-loss sum a0

is taken as the sum of channel counts (above background) up to channel nsep.Any

discontinuities in the data (e.g., obtained through separate CCD readouts) must be

removed by prior editing.

The data are transferred to the nn elements of an array d, subtracting any back-

ground and shifting the spectrum, so that the ﬁrst channel corresponds to zero energy

loss. The data are extrapolated to the end of the array by ﬁtting the last 10 data

channels to an inverse power law, using Eq. (4.51), then a cosine bell function is

subtracted to make the data approach zero at the end of the array without a disconti-

nuity in intensity or slope at the last recorded data point d(nﬁn). The zero-loss peak

is copied from array d and the discontinuity at the separation point (nsep) is removed

by subtracting a cosine bell function, a procedure that preserves the zero-loss sum

as a0.

An effective width fwhm1 of the zero-loss peak is estimated from the peak height

and area, taking the peak shape to be Gaussian. The program then asks for a choice

of reconvolution function: either the zero-loss peak (if zero is entered) or a Gaussian

peak of speciﬁed width fwhm2. If this width is the same as fwhm1, there is no peak

sharpening and no noise ampliﬁcation, but peak-shape distortion due to an asym-

metric resolution function is corrected. Discrete Fourier transforms are computed,

replacing the original data in d and z. The Fourier coefﬁcients are manipulated

according to Eq. (4.10), allowing scattering parameters up to t/λ = π to be

B.7 Drude Simulation of a Low-Loss Spectrum 409

accommodated. The higher-frequency coefﬁcients are attenuated to avoid noise

ampliﬁcation, using a Gaussian ﬁlter function or by multiplying by the Fourier trans-

form of Z(E). An inverse transform is then computed, giving the single-scattering

distribution (without zero-loss peak) as the real coefﬁcients in array d and in the

output ﬁle Flog.ssd. Prior division by the number nn of real data points ensures that

the output is correctly scaled.

The program F

LOGS works for thicker specimens (t/λ > π), using the procedure

described by Spence (1979). Channels nn/2 to nn of the array d are set to zero before

computing the Fourier transform. After applying Eq. (4.20) and taking an inverse

transform, channels nn/2 to nn contain a mirror image of the single-scattering dis-

tribution, which is discarded before writing the ﬁrst nn/2 channels to the output ﬁle

LOGS.SSD.

B.6 Maximum-Likelihood Deconvolution

RL UCY uses the Richardson–Lucy method of maximum-likelihood deconvolution

and can sharpen spectral data (improving the energy resolution) to an extent depen-

dent on the noise content of the original spectrum. It is based on C-code kindly

supplied by Lijun Wu and can be tested using S

PECGEN.PSD as input.

For spectral sharpening, the kernel is a zero-loss peak, supplied either as a sep-

arate ﬁle or stripped from the low-loss spectrum. In the case of core-loss data, the

kernel can be the zero-loss peak (for spectral sharpening only) or the low-loss spec-

trum, in which case plural (plasmon + core-loss) scattering is removed, in addition

to any sharpening. To avoid end-of-range artifacts, the intensity at the start and end

of the data array should be roughly matched, although this criterion is less impor-

tant than for Fourier deconvolution methods. In the case of a background-subtracted

ionization edge, the matching can be achieved by extrapolating the intensity to zero

at high energy loss. For an edge with background, it is sufﬁcient to adjust the energy

width of the data, so that the intensities at both ends of the data array are equal

(Egerton et al., 2008).

The program provides the option of dividing input data by a gain-reference spec-

trum and subtracting either a dark-current spectrum or a constant dark current, if

these operations were not already performed. The number N of iterations must be

speciﬁed; N = 15 is typical but several values should be tested. The energy resolu-

tion in the data improves with increasing N, and an estimate of the resolution (for

agivenN) can be obtained by using the same low-loss spectrum as both data and

kernel (Egerton et al., 2008).

B.7 Drude Simulation of a Low-Loss Spectrum

The program DRUDE calculates a single-scattering plasmon-loss spectrum for

a specimen of a given thickness tnm (in nm), recorded with electrons of a

speciﬁed incident energy e0 by a spectrometer that accepts scattering up to a

speciﬁed collection semi-angle beta. It is based on the extended Drude model

410 Appendix B: Computer Programs

(Section 3.3.2), with a volume energy-loss function elf in accord with Eq. (3.64) and

a surface-scattering energy-loss function srelf as in Eq. (4.31). Retardation effects

and coupling between the two surface modes are not included. The surface term can

be made negligible by entering a large specimen thickness (tnm > 1000).

Surface intensity srﬁnt and volume intensity volint are calculated from

Eqs. (4.31) and (4.26) , respectively. The total spectral intensity ssd is written to

the ﬁle D

RUDE.SSD, which can be used as input for KRAKRO. These intensities are

all divided by I

,togiverelative probabilities (per eV). The real and imaginary parts

of the dielectric function are written to D

RUDE.EPS and can be used for comparison

with the results of Kramers–Kronig analysis (K

RAKRO .DAT ).

Written output includes the surface-loss probability P

obtained by integrating

srﬁnt (a value that relates to two surfaces but includes the negative begrenzungs

term), for comparison with the analytical integration represented by Eq. (3.77).The

volume-loss probability P

is obtained by integrating volint and is used to calcu-

late the volume plasmon mean free path (lam = tnm/P

). The latter is listed and

compared with the MFP obtained from Eq. (3.44), which represents analytical inte-

gration assuming a zero-width plasmon peak. The total probability (P

= P

)is

calculated and used to evaluate the thickness (lam.P

) that would be given by the for-

mula t/λ = ln(I

), ignoring the surface-loss probability. Note that P

will exceed

1 for thicker specimens (t/λ > 1), since it represents the probability of plasmon

scattering relative to that of no inelastic scattering.

The command-line usage is Drude(ep,ew,eb,epc,beta,e0,tnm,nn), where ep is the

plasmon energy, ew the plasmon width, eb the binding energy of the electrons (0 for

a metal), and nn is the number of channels in the output spectrum. An example of

the output is shown in Fig. B.1a,b.

B.8 Kramers–Kronig Analysis

The program KRAKRO calculates the real part ε

(E) and imaginary part ε

(E)ofthe

dielectric function, as well as the s pecimen thickness t and mean free path λ(β)for

inelastic scattering. It employs the Fourier procedure for Kramers–Kronig analysis

described by Johnson (1975), but using fast-Fourier transforms. As input, it requires

a single-scattering distribution with no zero-loss peak but with its ﬁrst channel corre-

sponding to E =0 (as generated by D

RUDE.SSD). The program also requires values

of the zero-loss integral a0, incident-electron energy e0, collection semi-angle beta,

and optical refractive index ri. In the case of a metallic specimen, any large value

(>20) can be entered for ri.

The single-scattering intensity S(E) is read and transferred to the arrays ssd and

d, each of adequate length nn = 2

, where k is an integer. Assuming a Lorentzian

angular distribution, an aperture correction is applied to S(E) to make the result pro-

portional to Im(−1/ε); the proportionality constant rk = K is evaluated by utilizing

the Kramers–Kronig sum rule, Eq. (4.27). Since K = I

t/(π a

) according to

Eq. (4.26), this leads to an initial estimate of specimen thickness and mean free path,

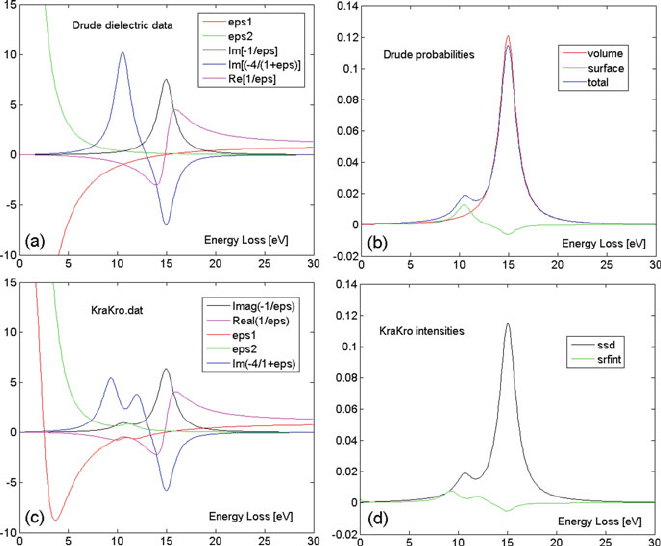
B.8 Kramers–Kronig Analysis 411

Fig. B.1 (a) Dielectric data generated by Drude for ep = 15, ew = 2, eb = 0, epc = 0.1,

e0 = 100, beta = 5, nn = 300, tnm = 50. (b) Drude bulk, surface, and total intensities, given as

dP/dE in eV

–1

.(c) Dielectric data generated in the ﬁrst iteration by KraKro with a0 = 1, ri = 1000,

and δ = 0.1, giving t = 56 nm (t = 47 nm in second iteration). (d) KraKro total and surface-mode

intensities (in eV

–1

) generated in ﬁrst iteration

evaluated as λ = t/(t/λ) = tI

where I

is the integral of S(E). Then Im( −1/ε)

is copied to the array di before being converted to its Fourier transform, the imagi-

nary part of d becoming the sine transform of Im(−1/ε). With appropriate scaling

(/nn) these coefﬁcients are converted into the real part of d and an inverse (cosine)

transformation yields Re(1/ε)−1, accompanied by its reﬂection about the midrange

(nn/2) axis, due to aliasing. Taking the high-energy tail to be proportional to E

−2

this energy dependence is subtracted from the lower energy (< nn/2) data and used

to extrapolate the high-energy values, a procedure that becomes less critical if nn is

made considerably larger than the minimum required value.

Knowing Re(1/ε) and Im (−1/ε), the real part eps1 and imaginary part eps2 of

ε are computed, followed by the surface energy-loss function srfelf and the surface-

scattering intensity srﬁnt, these data being written to the output ﬁle K

RAKRO .DAT .

The written output is truncated to the original range (nlines) of the input data.

Calculation of the surface-mode scattering is based on Eq. (4.31), which assumes

clean (unoxidized) and smooth surfaces that are perpendicular to the incident beam,

neglecting coupling between the surfaces (1/R

= 1+ε). The volume-loss intensity,

412 Appendix B: Computer Programs

obtained by subtracting srﬁnt from ssd, is then renormalized by re-applying the K–K

sum rule, leading to revised estimates for the specimen thickness and inelastic mean

free path. Kramers–Kronig analysis is then repeated to yield revised values of the

dielectric data.

By setting nloops > 2, further iterations are possible. Whether convergence is

obtained depends on the behavior of the data at low energy loss (E < 5eV).Toaid

stability, E is replaced by E + δ in the expression for the surface-scattering angular

dependence adep, thereby avoiding a non-zero value of srﬁnt at E = 0. For thicker

samples, δ = 0.1 eV is sufﬁcient but if surface losses are predominant, δ ≈ 0.5 eV

may be needed to ensure iteration stability (Alexander et al., 2008). An example of

the data output is given in Fig. B.1(c,d).

B.9 Kröger Simulation of a Low-Loss Spectrum

The program KROEGER evaluates the differential scattering probability d

P/d dE

in the low-loss region for a chosen incident energy, specimen thickness, collection

semi-angle, and eV/channel, based on Eq. (3.84a). As input it requires (E, ε

, ε

)

data, as provided by D

RUDE.EPS for example, together with values of incident

energy, specimen thickness, and collection semi-angle. The calculation procedure

is similar to that used in the Cerenkov script written for Digital Micrograph by

Wilfried Sigle.

As output, a three-dimensional contour plot is generated, including all terms in

Eq. (3.84a), and a separate plot that represents only t he ﬁrst (volume) term, equiv-

alent to Eq. (3.70). Other two-dimensional plots represent the angular dependence

at selected energy losses and the energy-loss spectrum at a particular (e.g., zero)

scattering angle, these selected values being speciﬁed within the program. The prob-

ability is integrated (over the input value of angular range β)togivedP/dE. The

integration uses a MATLAB function quadl, which may need to be replaced if the

program is run using Octave.

A s eparate program K

ROEGEREBPLOTS demonstrates some of the physics

behind retardation effects by plotting data for 10 different thicknesses and spec-

iﬁed β, E, and E

, using as input (for example) DRUDE.EPS or silicon data

ROEGEREBPLOTS_SI.DAT). Angular dependences are plotted for a ﬁxed E, for

comparison with ﬁg. 3 of Erni and Browning (2008), where E = 3 eV and

= 200 keV. Energy dependences of dP/dE are then plotted, integrated up to

a scattering angle β for comparison with Fig. 3.26b (ﬁg. 4a of Erni and Browning),

where E

= 300 keV, β = 2.1 mrad.

B.10 Core-Loss Simulation

COREG EN constructs an idealized core-loss proﬁle based on a power-law (AE

−r

)

single-scattering distribution but with plural (plasmon + core-loss) scattering

included. It uses Eq. (3.117), the plasmon-loss spectrum being taken to be a series of

B.11 Fourier Ratio Deconvolution 413

delta functions obeying Poisson statistics. The plasmon-loss and core-loss spectra

are displayed and written to the ﬁles C

OREGEN.CORE and COREGEN.LOW, which

can be used as input for testing the deconvolution program F

RAT.

DGEGEN adds a power-law background (with the same exponent r)tothe

OREGEN output, giving an output similar to Fig. 3.33. The jump ratio of the edge

(ratio of intensities just after/before the threshold) is speciﬁed as an input parame-

ter. To avoid artifacts, the maximum order n of the plasmon-scattering contribution

to the background is limited, ensuring that the AE

−r

formula is not applied for

E < 30 eV. The plasmon-loss and core-loss spectra are displayed and written to

DGEGEN.CORE and EDGEGEN.LOW.

B.11 Fourier Ratio Deconvolution

Using the Fourier ratio method described in Section 4.3.2, the program FRAT

removes plural scattering from an ionization edge whose background has previously

been subtracted. It requires a low-loss spectrum, recorded from the same region of

specimen at the same eV/channel, but this spectrum need not be contiguous with the

core-loss region or match it in terms of relative intensity. The method is therefore a

more practical alternative to F

are obtained in separate readouts. Other advantages are that the zero-loss peak does

not need to be extracted from the low-loss spectrum (which involves some approxi-

mation) and that the specimen thickness i s in principle unlimited (there are no phase

ambiguities in the Fourier components).

The low-loss spectrum is read as two-column (x,y) data from a named input ﬁle

and the zero-loss channel is taken as the ﬁrst maximum. The ﬁrst minimum is found

in order to estimate the zero-loss integral a0 and the energy resolution (obtained

from a0 and the zero-loss peak height, assuming a Gaussian shape). The spectrum

is transferred to a working array d, containing nn channels where nn is the next

power of 2 that exceeds the actual number of low-loss data channels.

Data are shifted within d, so that the ﬁrst channel represents zero loss. Any

background (average of the ﬁrst ﬁve channels) is subtracted and the intensity is

extrapolated to zero at the last channel, using a power-law extrapolation with cosine

bell termination. Then the left half of the zero-loss peak is added to the end channels

of the array. The energy resolution (FWHM of the zero-loss peak) is displayed, to

serve as a guide when specifying the width of the reconvolution function; smaller

widths lead to peak sharpening but with a severe noise penalty, as explained in

Section 4.3.2. Even without sharpening, the effect of any tails on the zero-loss

peak (due, for example, to the detector point-spread function) can be successfully

removed from core-loss data.

The core-loss spectrum is read into odd elements of an array c and extrapo-

latedtozerointhesamewayasd. After taking Fourier transforms, the Fourier

coefﬁcients are processed according to Eq. (4.38), using a Gaussian reconvolu-

tion function gauss. If the coefﬁcient of this function is the zero-loss integral a0,

414 Appendix B: Computer Programs

plural scattering is subtracted from the ionization-edge intensity; if the coefﬁcient

is changed to the total integral (at) of the low-loss spectrum, the core-loss SSD will

have the same integral as the original edge, as needed for absolute elemental analysis

of thick specimens (Wong and Egerton, 1995).

B.12 Incident-Convergence Correction

The program CONCOR2 evaluates the factor F

by which inelastic intensity (at

energy loss E and recorded using a collection semi-angle β) is reduced as a result of

the convergence of the electron probe (semi-angle α). The program also evaluates

the factor F

(for use in absolute quantiﬁcation) and the effective collection angle

∗

deﬁned by Eq. (4.73). For inner-shell scattering, the energy loss E can be taken

as the edge energy E

or (better) as an average energy loss (E

+ /2) within the

integration window.

ONCOR2 uses an analytical formula (Scheinfein and Isaacson, 1984) that

assumes that the incident beam intensity per steradian is constant up to the angle α

and that the angular distribution of the inelastic scattering remains Lorentzian up to

an angle equal to α + β.

When analyzing for two elements, a and b, incident beam convergence is taken

into account by multiplying the areal density ratio N

, derived from Eq. (4.66),

by F

(or by F

). If the absolute areal density N

of an element a is

being calculated from Eq. (4.65), the result should be divided by F

.Forα<β,

= F

;forα>β, F

is larger than F

(and may exceed unity; see Fig. 4.19)

because the collection angle cuts off part of the low-loss angular cone. As an alter-

native to applying the correction factors F

or F

, incident beam convergence can

be incorporated by computing each ionization cross section for the effective collec-

tion angle bstar, which is a function of energy loss and therefore different for each

element.

B.13 Hydrogenic K-Shell Cross Sections

The program SIGMAK3 uses a hydrogenic approximation for the generalized oscil-

lator strength, Eqs. (3.125), (3.126), and (3.127), to calculate differential and

integrated cross sections and dipole oscillator strengths (f 0) for K-shell ionization.

Unlike the original

SIGMAK (Egerton, 1979) and SIGMAK2 programs, the reduction

in effective nuclear charge (due to screening by the second 1s electron) is taken

as 0.50 rather than the value of 0.3125 calculated by Zener (1930) for ﬁrst-row

elements, the aim being to provide a closer match to EELS, photoabsorption, and

Hartree–Slater data (Egerton, 1993). The effect of this change becomes more sig-

niﬁcant at low atomic number: f(100 eV) is reduced from 0.46 to 0.42 for oxygen

and from 2.02 to 1.58 for lithium.

B.14 Modiﬁed-Hydrogenic L-Shell Cross Sections 415

Relativistic kinematics is employed, based on Eqs. (3.139), (3.140), (3.144), and

(3.146), but retardation effects (Appendix A) are not included. To improve accu-

racy, the energy-differential cross section dsbyde is obtained by integrating df/dE

(gosfunc in the program) over a logarithmic grid, as in Eq. (3.151), with limits of

integration given by Eqs. (3.152) and (3.153). The energy-differential cross sec-

tion dsbyde is integrated to give the partial cross section sigma, making use of the

E-dependence described by Eq. (3.154) in order to achieve reasonable accuracy for

a relatively large increment einc, taken as delta/10, delta being the integration win-

dow speciﬁed in the input. In the printed output, the integration is continued beyond

E = E

+ delta but with increasing energy steps, so that the integral cross section

(β) can be displayed as an asymptotic limit.

Total K-shell cross sections (as required for EDX spectroscopy, for example) can

be obtained as the value of σ

(β) after entering β = π = 3142 mrad, delta ≈

100 eV and taking the asymptotic value of sigma corresponding to large .For

≤ 300 keV, these cross sections are within 3% of the Hartree–Slater values

quoted by Scoﬁeld (1978) for Ar and Ni.

Since the energy-differential cross section dσ /dE is independent of K-edge

threshold energy ek, its value at any scattering angle θ = β and energy loss E can

be displayed by setting delta = 0 and ek = E in the input data. Likewise, a K-loss

cross section sigma integrated between any two values of energy loss (E

and E

)

can be displayed by entering the lower energy loss as ek and the energy difference

– E

) as the speciﬁed integration window delta.

B.14 Modiﬁed-Hydrogenic L-Shell Cross Sections

SIGMAL3 evaluates cross sections (in barn = cm

×10

–24

)forL-shell ionization

by fast incident electrons. It uses relativistic kinematics (without retardation) and

an expression for the generalized oscillator strength (Choi et al., 1973) based on

hydrogenic wavefunctions, with the screening constants recommended by Slater

(1930). To more correctly match observed edge shapes, the generalized oscilla-

tor s trength is multiplied by a correction factor rf, calculated for each energy loss

through the use of an empirical parameter xu. Values of xu, together with the L

and

threshold energies of each element, are tabulated at the beginning of the program.

Approximate allowance for white-line peaks, for 18 ≤ Z ≤28, is made by using the

full-hydrogenic oscillator strength (rf =1) within 20 eV of the L

threshold. In other

respects, the calculation follows the same procedure as S

IGMAK3.

Values of xu are modiﬁed from those of S

IGMAL and SIGMAL2, so that the

program gives integrated oscillator strengths f(100 eV) equal to tabulated values

(Egerton,1993) based on Hartree–Slater, EELS, and photoabsorption data. The pro-

gram gives an output for the elements Al to Kr inclusive, although probably with

less accuracy toward the ends of that range. The algorithm is not designed to pro-

vide accurate values of the differential cross section dsbyde within 50 eV of the

ionization edge or to properly simulate the Bethe ridge at high scattering angle.

416 Appendix B: Computer Programs

As with S IGMAK3, total L-shell cross sections can be obtained by entering

β = 3142 mrad and taking the asymptotic value of sigma (corresponding to large

); for E

≤ 300 keV, the program yields cross sections which are within 8% of

those calculated by Scoﬁeld (1978) for Ar and Ni.

B.15 Parameterized K-, L-, M-, N-, and O-Shell Cross Sections

The program SIGPAR2 calculates the partial cross section σ

(β, )ofamajorion-

ization edge using Eq. (A.7), which embodies the relativistic oscillator strength and

kinematics for an isotropic material. It is valid only for a limited collection angle,

falling within the dipole region: β<<(E/E

)

1/2

, since it uses values of optical

oscillator strength f() (together with estimates of their accuracy) that are stored

in the ﬁles

FK.DAT, FL.DAT , FM23.DAT, FM45.DAT and FNO45.DAT. These values

represent best estimates (Egerton, 1993) based on Hartree–Slater calculations, x-ray

absorption data, and EELS measurements.

The integration window  should be within the range 30–250 eV; linear interpo-

lation or extrapolation is used to estimate f() for values of  other than those used

in the tabulations. In the case of M

edges only  = 30 eV values are given, based

on EELS measurements of Wilhelm and Hofer (1992). If the semi-angle β lies out-

side the dipole region (taken here to be half the Bethe ridge angle), a warning is

given to indicate that the calculated cross section will be too large. Because retarda-

tion effects are included, the results should be valid for incident electron energies as

high as 1 MeV.

B.16 Measurement of Absolute Specimen Thickness

The program tKKs calculates the thickness of a specimen whose low-loss spectrum

is supplied in the form of two-column (E, intensity) data. The algorithm is based

on the Kramers–Kronig sum rule, with approximate allowance for plural scattering

based on Eq. (5.9). A surface-mode correction term t can be invoked internally as

an option. Because Eq. (5.9) is a dipole formula, the spectral data should correspond

to a small collection angle: β<θ

, where θ

≈ (

E/E

)

1/2

is a Bethe-ridge angle for

some mean energy loss

E.Ifβ>θ

, with

E taken as 50 eV, the program issues a

warning and replaces β with θ

to avoid a misleading answer.

In place of a recorded low-loss spectrum, S

PECGEN.PSD can be used as input

data. In either case, the zero-loss integral is entered as zero to indicate that the zero-

loss peak must be identiﬁed, its integral calculated as I0 and a correction factor C

evaluated to make approximate allowance for plural scattering in the input data.

Alternatively, S

PECGEN.SSD,DRUDE.SSD,oranysingle-scattering spectrum

with no zero-loss peak (e.g., a measured spectrum after F

LOG deconvolution) can be

used as input to

T KKs. An appropriate value of the zero-loss integral must then be

supplied; this value is 1 in the case of D

RUDE.SSD, which represents probabilities

B.18 Constrained Power-Law Background Fitting 417

relative to the zero-loss integral. The plural scattering correction factor C is set to 1,

since plural scattering peaks are absent.

B.17 Total Inelastic and Plasmon Mean Free Paths

The program IMFP calculates inelastic mean free paths for a given material,

for speciﬁed incident energy E

, probe convergence semi-angle α and spectrum

collection semi-angle β. Separate calculations are made, using the formulas of

Malis et al. (1988), Jin and Li (2006), and Iakoubovskii et al. (2008a). Correction

for incident-probe convergence is included, in the ﬁrst two cases by use of the

Scheinfein–Isaacson formula employed in CONCOR2. If the effective collection

angle β

∗

exceeds the Bethe-ridge angle (E

)

1/2

, the program gives a warning

that dipole conditions are violated (the formulas of Malis et al. and of Jin and Li

include no dipole-region cutoff).

In the case of a compound, the atomic number Z

, atomic weight A

, and atomic

fraction f

are entered for each component until

reaches 1. An effective atomic

number Z

eff

is then evaluated using Eq. (5.4), and for Jin and Li (2006) an effective

atomic weight using the same procedure. If the specimen is a material whose mean

energy loss E

is known (Table 5.2), λ may be more accurately calculated using the

program PMFP.

PMFP calculates an inelastic mean free path based on a free-electron zero-

damping approximation, if given values of the incident energy E

, a mean energy

loss E

, incident convergence semi-angle α, and collection semi-angle β. It ﬁrst

evaluates the effective collection angle β

∗

and then estimates the dipole cutoff angle,

the latter being taken as a Bethe-ridge angle θ

= (E

)

1/2

.Ifβ

∗

<θ

, a dipole

mean free path λ(β

∗

) is calculated, using Eq. (5.2). Otherwise, the total-inelastic

mean free path is λ(θ

) i s printed.

PMFP can also be used to calculate a plasmon cross section, using Eq. (3.58) with

the plasmon energy E

replacing E

. The dipole value λ

(β) is printed if β

∗

<θ

)

1/2

and otherwise the total plasmon cross section λ

(θ

B.18 Constrained Power-Law Background Fitting

The program AFIT interpolates a power-law (AE

–r

) background between two ﬁtting

regions, using linear least-squares ﬁtting according to Eqs. (4.46) and (4.47).The

ﬁtted background passes through the middle of the data in both halves of the ﬁtting

region, making the background-subtracted intensity approximately zero at both ends

of its range.

The program B

FIT is used for obtaining a more accurate core-loss integral

(Egerton and Malac, 2002). Pre-edge and post-edge energy windows are chosen,

just below and far above the threshold energy, as in A

FIT. A ﬁrst-estimate interpo-

lated background is obtained, based on a generalization of Eq. (4.51) rather than on