Egerton R.F. Electron Energy-Loss Spectroscopy in the Electron Microscope

Подождите немного. Документ загружается.

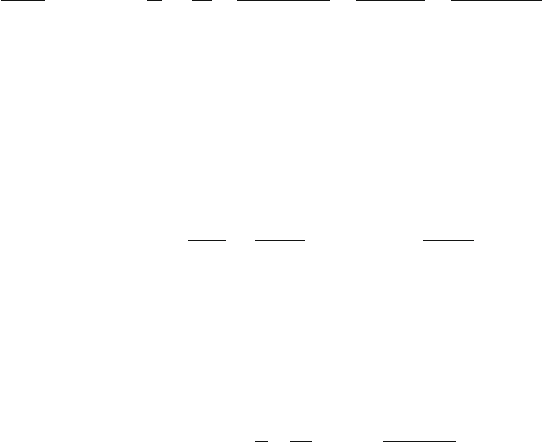
Appendix A

Bethe Theory for High Incident Energies

and Anisotropic Materials

Even for 100-keV incident electrons, it is necessary to use relativistic kinematics

to calculate inelastic cross sections, as in Section 3.6.2. Above 200 keV, however,

an additional effect starts to become important, representing the fact that the elec-

trostatic interaction is “retarded” due to the ﬁnite speed of light. At high incident

energies and for isotropic materials, Eq. (3.26) should be replaced by (Møller, 1932;

Perez et al., 1977)

d dE

= 4γ







−

2γ −1

Q(E

−Q)

)



η(q, E)

(A.1)

where γ = 1/(1 −v

)

1/2

, v is the incident electron velocity, a

= 52.92 pm is

the Bohr radius, R = 13.6 eV is the Rydberg energy, and m

= 511 keV, the rest

energy of an electron. For most collisions, the last three terms within the brackets of

Eq. (A.1) can be neglected and the ratio (k

) of the fast-electron wavenumbers

(after and before scattering) can be taken as unity. The quantity Q has dimensions

of energy and is deﬁned by

Q =



−

= R(qa

)

−

(A.2)

where q is the scattering vector and E represents energy loss. The E

/2m

term in

Eq. (A.2) can become signiﬁcant at small scattering angles.

In Eq. (A.1),

n(q, E)

is an energy-differential relativistic form factor, equal

to the nonrelativistic form factor

ε(q, E)

in the case of high-angle collisions but

given for qa

<< 1 by (Inokuti, 1971):

η(q, E)





Q −

2γ



(A.3)

where df/dE is the energy-differential generalized oscillator strength employed in

Sections 3.2.2 and 3.6.1.

According to Fano (1956), the differential cross section is a sum of two indepen-

dent terms (incoherent addition) and within the dipole region, θ << (E/E

)

1/2

,his

result can be written as

399

R.F. Egerton, Electron Energy-Loss Spectroscopy in the Electron Microscope,

DOI 10.1007/978-1-4419-9583-4_6,



Springer Science+Business Media, LLC 2011

400 Appendix A: Bethe Theory for High Incident Energies and Anisotropic Materials

d dE

(E/R)(T/R)







+θ

(v/c)

(θ

+θ

)(θ

+θ

/γ

)



(A.4)

where T = m

/2 and θ

= E/(γ m

) = E/(2γ T) as previously. The ﬁrst term

is identical to Eq. (3.29) and gives the Lorentzian angular distribution observed at

lower incident energies. It arises from Coulomb (electrostatic) interaction between

the incident and atomic electrons and involves forces parallel to the scattering

vector q.

The second term in Eq. (A.4) represents the exchange of virtual photons involv-

ing forces perpendicular to q (transverse excitation). This term is zero at θ = 0

and negligible at large θ , but can be signiﬁcant for small scattering angles. I t

becomes more important as the incident energy increases: for E

> 250 keV it

shifts the maximum in the angular distribution away from zero angle, as illustrated

in Fig. A.1. This angular dependence has been conﬁrmed by energy-ﬁltered diffrac-

tion patterns of the K-shell excitation in graphite by 400-keV and 1-MeV electrons

(Kurata et al., 1997). The displaced maximum should not be confused with the Bethe

ridge (Sections 3.5 and 3.6.1), which occurs at higher scattering angles and only for

energy losses well above the binding energies of the electrons involved.

Fig. A.1 Differential cross

section for K-shell scattering

in aluminum, at an energy

loss just above the ionization

edge, calculated for three

values of incident-electron

energy using a hydrogenic

expression for df/dE. Solid

curves include the effect of

retardation; the dashed curves

do not. From Egerton (1987),

Optics

Appendix A: Bethe Theory for High Incident Energies and Anisotropic Materials 401

Integration of Eq. (A.4) up to a collection angle β gives

dσ

4πa

(E/R)(T/R)



ln(1 +β

/θ

) +G(β, γ , θ

)



(A.5)

where

G(β, γ , θ

) = 2lnγ − ln



+θ

/γ



−



+θ

/γ



(A.6)

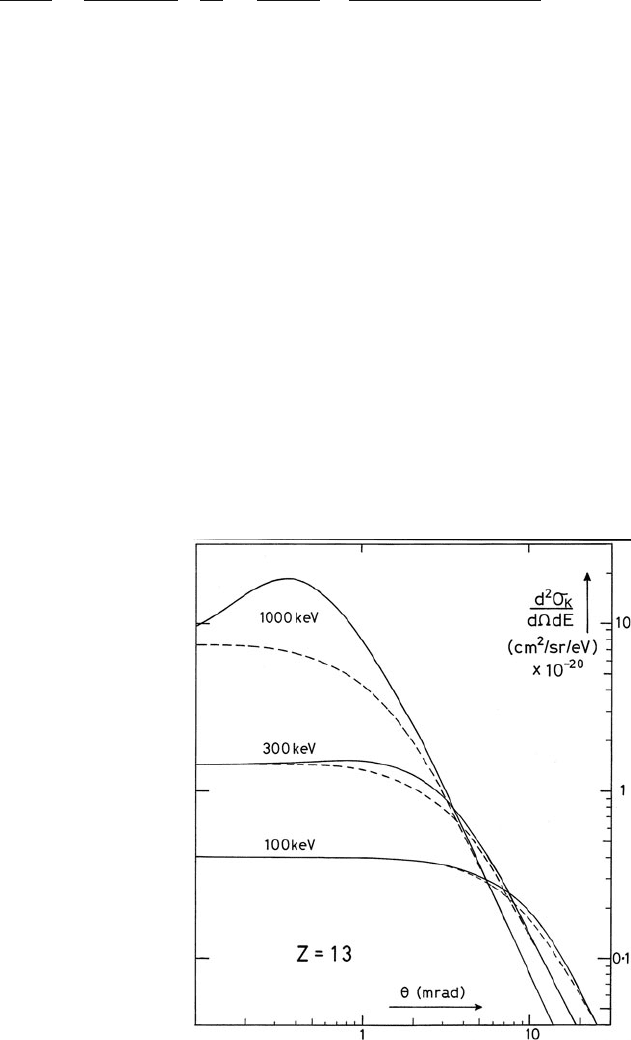
The retardation term G(β, γ , θ

) exerts its largest effect at β ≈ θ

and increases the

energy-loss intensity by 5% to 10% for E

= 200 keV, and by larger amounts at

higher incident energy; see Fig. A.2. Under certain conditions, this increase in cross

section results in the emission of

Cerenkov radiation (Section 3.3.4); when Q = 0,

E = pc, giving a resonant condition with photons. For β>>θ

but still within the

dipole region, Eq. (A.5) simpliﬁes to an alternative form given by Fano (1956).

For an ionization edge whose threshold energy is E

,Eq.(A.5) can be integrated

over an energy range  that is small compared to E

to give

(β, ) =

4πa

(





)(

T/R

)

f ()





1 +β







(

β, γ ,





)



(A.7)

where E and θ

 are average values of E and θ

within the integration region.

Numerical evaluation shows that Eq. (A.7) is a better approximation if a geometric

(rather than arithmetic) mean is used, so that E=

[

(

+

)

]

1/2

and θ

=

E/2γ T. This equation can be used to calculate cross sections for EELS elemental

Fig. A.2 Percentage increase in cross section (for four values of incident energy) as a result of

relativistic retardation, according to Eq. (A.7)

402 Appendix A: Bethe Theory for High Incident Energies and Anisotropic Materials

analysis from tabulated values of the dipole oscillator strength f(), as in the SIGPAR

program (Appendix B).

If the i ntegration is carried out over all energy loss, the result is the Bethe

asymptotic formula for the total ionization cross section for an inner shell, used

in calculating x-ray production:

4πa

(

)(

T/R

)







+2lnγ −



(A.8)

where N

is the number of electrons in the shell k (2, 8, and 18 for K, L, and M

shells); b

and c

are parameters that can be parameterized on the basis of experi-

mental data (Zaluzec, 1984). As seen from Eq. (A.8), a Fano plot of v

against

)

/(c

−v

) −v

should yield a straight line even at megaelectron volt ener-

gies (Inokuti, 1971). The last two terms i n Eq. (A.8) cause σ

to pass through a

minimum and exhibit a relativistic rise when the incident energy exceeds about

1MeV.

A.1 Anisotropic Specimens

The equations above are believed to be relativistically correct for a specimen that is

isotropic in its physical properties, such as an amorphous material or a cubic crys-

tal. Anisotropic materials are more complicated because their dielectric properties

depend on the direction of q, and therefore on the angle  between the incident

beam and the z-axis (Fig. 3.60a).

We illustrate this situation by considering the case of a uniaxial material such

as graphite or hexagonal boron nitride (h-BN), in which the atoms lie in layers

containing the x- and y-axes, separated by a larger interatomic distance (and weaker

bonding) in the perpendicular z-direction. In the xy-plane there are three hybridized

σ-bonding orbitals per atom (formed from 2s,2p

, and 2p

atomic orbitals) and in

the z-direction a π-bonding orbital (formed from 2p

) directed perpendicular to the

layers. At higher energy lie the associated unﬁlled σ

∗

and π

∗

antibonding states; the

excitation of K-shell electrons involves both 1s →σ

∗

and 1s → π

∗

transitions, their

relative strengths depending on the angle  (Leapman et al., 1983).

Using relativistic theory, Eqs. (3.169) and (3.170) become, for the angular

dependence of these two components (Souche et al., 1998; Radtke et al., 2006):

∝

(γ

−2

cos  −θ

sin )

(θ

+γ

−2

)

(A.9)

∝

(γ

−2

sin  +θ

cos )

+θ

(θ

+γ

−2

)

(A.10)

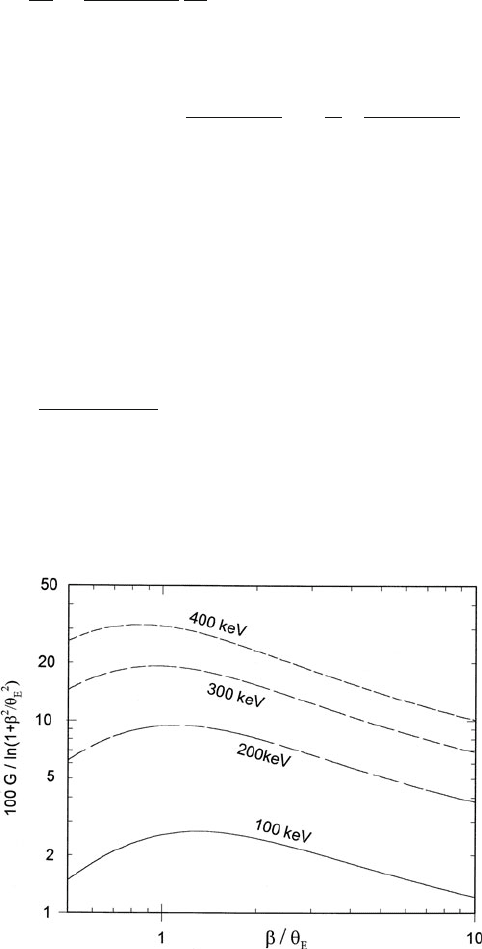
A.1 Anisotropic Specimens 403

Fig. A.3 Intensities J

, J

, and their sum, calculated from Eqs. (A.9), (A.10), and (A.11)for

 = 0 and 300 keV incident electrons, compared to the equivalent quantities calculated from

non-relativistic theory (γ = 1)

where θ

= θ

+θ

. Considering the  = 0 case for simplicity: the angular widths

of both J

and J

are reduced as a result of the γ

–2

term in the denominators of

Eqs. (A.9) and (A.10), but whereas J

is reduced in amplitude, J

is increased; see

Fig. A.3. Therefore the angular width of the total (J

and J

) intensity is broadened,

because of the J

peaks at a non-zero angle (θ = θ

/γ ); see Fig. A.3.

For an isotropic material, Eqs. (A.19) and (A.10) give the total intensity as

tot

= J

∝

+γ

−4

(θ

+γ

−2

)

(A.11)

which is independent of specimen tilt  but has a somewhat non-Lorentzian distri-

bution because of the γ

–2

and γ

–4

factors. For E

> 250 keV, the total intensity

peaks away from θ =0, reﬂecting the larger relative contribution from the transverse

component, just as in Fig. A.1. Radtke et al. (2006) recorded energy-ﬁltered scat-

tering patterns at the π- and σ-peak energies of graphite (Fig. 3.60b), using incident

energies of 200 and 300 keV. Although the differences were not large, the relativistic

equations were found to give better agreement with experiment.

Schattschneider et al. (2005) explain how longitudinal and transverse compo-

nents of momentum transfer must be treated differently in the case of an anisotropic

material. Due to relativistic contraction in the direction of motion, the electric ﬁeld

of a sufﬁciently fast electron is no longer spherically symmetric, resulting in a

greater relative contribution from excitations transverse to the motion. In terms

of the formulation of Fano (1956), this means that the longitudinal and transverse

contributions cannot be added incoherently in anisotropic materials; the transition

matrix is not a spherical tensor and interference terms in the dynamic form factor

404 Appendix A: Bethe Theory for High Incident Energies and Anisotropic Materials

Table A.1 Magic angle θ

in units of θ

and in

milliradians (for E = 284 eV)

as a function of incident

energy, according to

Schattschneider et al. (2005)

(keV) θ

/θ

(mrad)

50 2.92 8.68

100 2.25 3.48

150 1.79 1.91

200 1.46 1.21

300 1.22 0.60

400 0.78 0.35

500 0.61 0.23

1000 0.25 0.05

cannot be neglected. These terms are of the order of 20% for E

= 200 keV and

proportional to (v/c)

. However, the longitudinal (z) term is positive whereas the

perpendicular term is negative; they exactly cancel for an isotropic material, leaving

only a small relativistic correction, proportional to (v/c)

A further consequence of this interference effect is a small value of the magic

angle (Section 3.10). A spectrum recorded with a collection angle equal to θ

is identical to that recorded from a random-polycrystalline (orientation-averaged)

isotropic material because in this condition the π and σ interference terms exactly

cancel. Relatistivistic theory (Jouffrey et al., 2004; Schattschneider et al., 2005; Sun

and Yuan, 2005) predicts a rapid fall in θ

with increasing incident energy; see

Table A.1.

Appendix B

Computer Programs

The computer codes discussed in this appendix generate spectra, process spectral

data, or calculate scattering cross sections or mean free paths. They are designed as

a supplement to Digital Micrograph scripts (Mitchell and Schaffer, 2005) and can

be downloaded from http://tem-eels.com or from http://tem-eels.ca

All are written in MATLAB script. A program to convert DigitalMicrograph data

ﬁles into MATLAB format is available. As these programs may be updated from

time t o time, the description that follows in this appendix may not be exact.

Each program can be run in several ways:

1. From the MATLAB Editor window, via the Run (F5) command of the Debug

menu, or by clicking on the green triangle and entering input variables as

directed;

2. By typing the appropriate ProgramName(InputParameters) as given at the begin-

ning of each program listing and as discussed below, this option being convenient

for repetitive use with minor changes to the input parameters;

3. Many of the programs can be run using the free Octave software available from

http://www.gnu.org/software/octave/download.html. Typically they are run by

typing the program name in a command window, then entering input parameters

as requested.

B.1 First-Order Spectrometer Focusing

PRISM calculates ﬁrst-order focusing properties of a single-prism spectrometer,

based on the matrix method: Eqs. (2.8), (2.9), (2.10), and (2.11). Beam displace-

ments (x,y) and angles (x



, y



) in radians are calculated for an entrance cone of

semi-angle 1 mrad and a speciﬁed distance v relative to the prism exit point. The

program then changes the image distance v to correspond to the calculated dis-

persion plane (where x = 0) and (x, y, x



, y



) values are recalculated. Second-order

matrices are not calculated; higher order focusing can usually be corrected by the

use of external multipoles.

405

R.F. Egerton, Electron Energy-Loss Spectroscopy in the Electron Microscope,

DOI 10.1007/978-1-4419-9583-4_7,



Springer Science+Business Media, LLC 2011

406 Appendix B: Computer Programs

Input is of the form: Prism(u, eps1, eps2, K1, g, R, phi, v), with symbols as used in

Section 2.2. An input of the form Prism(620, 16, 47, 0.4, 1.25, 100, 90, 90) produces

the following output:

For v = 90, x =−0.0121215, x



=−0.00322115, y =−0.0480911,



=−0.00742323

For v =86.2369, x = 0, x



=−0.00322115, y =−0.0201568, y



=−0.00742323

The dimensions u, v, R, and g can be expressed in any consistent set of units

(mm, cm). K1 = 0 implies a SCOFF approximation and gives results equivalent

to Eqs. (2.4) and (2.5); K1 ≈ 0.4 corresponds to mirror planes and tapered magnet

edges, the x-focusing is unchanged and the y-focusing is slightly weaker.

B.2 Cross Sections for Atomic Displacement and High-Angle

Elastic Scattering

SIGDIS calculates elastic cross sections for bulk (knock-on) atomic displacement

or electron-induced surface sputtering. It uses angle-integrated analytical formulas

based on the Rutherford and the McKinley–Feshbach–Mott approximations. For

Z > 35, the Rutherford value may be the more accurate (depending on the values of

Ed and E0). Input is of the form: SigDis(Z,A,Ed,E0).

The maximum energy transfer E

max

is obtained from Eq. (3.12b).Forbulk dis-

placement in common metals, the minimum transfer E

min

can be taken as the

displacement energy E

, which can be evaluated by applying Eq. (3.12c) to the

threshold energies tabulated by King et al. (1987).

For surface sputtering, cross sections are calculated for a minimum transfer

min

equal to the displacement energy E

(spherical escape potential) and also for

min

= (E

max

)

1/2

(planar surface potential), as discussed in Section 3.1.6.The

displacement energy E

can be taken as the sublimation energy E

sub

or as (5/3)E

sub

the latter being probably more accurate for metals (Egerton et al., 2010).

IGADF calculates Rutherford and McKinley–Feshbach–Mott cross sections

for elastic scattering between two speciﬁed angles, θ

min

and θ

max

, appropriate to

STEM measurements or imaging with a HAADF detector. Input is of the form:

SigADF(Z,A,qn,qx,E0) where qn and qx represent the minimum and maximum

angles. A warning is given if θ

min

is below the Lenz screening angle: θ

1/3

, indicating that screening and diffraction effects may make the result

inaccurate.

B.3 Lenz-Model Elastic and Inelastic Cross Sections

LENZPLUS calculates cross sections of elastic and inelastic scattering (integrated

over all energy loss) for an element of chosen atomic number, based on the atomic

model of Lenz (1954). It uses Eqs. (3.5) and (3.15) for the differential cross sections

B.4 Simulation of a Plural-Scattering Distribution 407

at a scattering angle β, Eqs. (3.6), (3.7) and a more exact version of Eq. (3.16) for

the cross sections integrated up to a scattering angle β, and Eqs. (3.8) and (3.17)

for the total cross sections (large β). Fractions F of the elastic and inelastic scat-

tering accepted by the angle-limiting collection aperture are also evaluated and are

likely to be more accurate than the absolute cross sections. The elastic-scattering

values are not intended to apply to crystalline specimens. Input is of the form

LenzPlus(E0,Ebar,Z,beta,toli), where toli denotes the inelastic scattering parame-

ter t/λ

that is used only in the second half of the program; a value of 0 terminates

the program halfway.

To provide inelastic cross sections, the Lenz model requires a mean energy loss

Ebar, a different average from that involved in the formula for mean free path

Eq. (5.2). Following Koppe, Lenz (1954)usedEbar = J/2, where J (≈ 13.5 Z)is

the atomic mean ionization energy. This option is invoked by entering Ebar = 0in

the program. From Hartree–Slater calculations, Inokuti et al. (1981) give the mean

energy per inelastic collision for elements up to strontium; values are in the range

20–120 eV and have an oscillatory Z-dependence that reﬂects the electron-shell

structure, which is appropriate for atoms but less so for solids.

If provided with a value of t/λ

(where λ

is the total-inelastic mean free path,

integrated over all scattering angles), L

ENZPLUS calculates the relative intensi-

ties of the unscattered, elastically scattered, inelastically scattered, and (elastic +

inelastic) components accepted by the collection aperture, including scattering up

to fourth order and allowing for the increasing width of the plural-scattering angu-

lar distributions, as described by Eqs. (3.97), (3.108), and (3.110). The expression

ln(I

) is calculated for comparison with t/λ

(β) to assess the effect of this angular

broadening.

B.4 Simulation of a Plural-Scattering Distribution

SPECGEN generates a series of Gaussian-shaped “plasmon” peaks, each of the form

exp[−(1.665E/E

)

], whose integrals satisfy Poisson statistics and whose full

widths at half maximum are given by

(E

)

= (E)

+n(E

)

(B.1)

Here E is the instrumental FWHM and E

represents the natural width of

the plasmon peak. This plural-scattering distribution (starting at an energy −ez

and with the option of adding a constant background back) is written to the ﬁle

PECGEN.PSD; the single-scattering distribution (with ﬁrst channel corresponding

to E = 0) is written to S

PECGEN.SSD to allow a direct comparison with the results

of deconvolution.

Input is of the form: SpecGen(ep,wp,wz,tol,a0,ez,epc,nd,back,fback,cpe). The

program approximates noise in an experimental spectrum in terms of two compo-

nents. Electron-beam shot noise (snoise) is taken as the square root of the number

of counts (for each order of scattering) but multiplied by a factor fpoiss, taken as

cpe

1/2

, where cpe is the number of counts per beam electron, assuming Poisson