Эддоус М., Стэнсфилд Р. Методы принятия решений
Подождите немного. Документ загружается.


Отвепаи
авторов моделей на экзаменационные
вопросы
555
Целевая функция:
Максимизировать ежедневный доход Р, где
Р = 18,2 R
+
14,2 S + 23,8 Т (ф. ст. в день)
В условиях следующих ограничений:
R, S, Т ^
О
Наличие авекс:
Наличие бумакс:
Наличие сидекс:
Наличие доракс:
Спрос на телтрейт:
0,4 R + 0,4 S
<.
200 кг в день,
0,2 S + 0,4 Т ^ 120 кг в день,
<,
250 кг в день,
^ 150 кг в день,
<,
500 кг в день.
0,3 R + 0.3 S + 0.2 Т
0,3 R +0,1 S + 0,4T
Т
б) Ниже показана итоговая симплекс-таблица:
Базис
S
Т
С
R
Е
R
0
0
0
1
0
0
5
1
0
0
0
0
0
т
0
1
0
0
0
0
А
1,875
-0,9375
-0,5625
0,625
0,9375
15,6875
В
2,5
1,25
-0,25
-2,5
-1,25
19,75
С
0
0
1
0
0
0
D
-2,5
1,25
-0,25
2,5
-1,25
39,75
Е
0
0
0
0
1
0
Значение
300
150
70
200
350
11,470
=s
=Т
=R
Итого
R, S, Т определены выше. А, В, С и D
—
неиспользуемые излишки рюсурюов
авекс, бумакс. сидекс и дорекс. е
—
количество химиката телтрейт, находящегося
в дефиците от максимального спроса на него, равного 500 кг в день. Оптималь-
ный план (его значения указаны в правом столбце симплекс-таблицы):
300 кг в день химиката сеноупур;
150 кг в день химиката телтрейт;
200 кг в день химиката ростик.
Максимальный доход составляет 11470 ф. ст. в день.
Использование сырья;
Из Правого столбца симплекс-таблицы следует, что С = 70 кг, т.е. 70 кг
ресурса сидекс не используется.
А = В =D=0.
Следовательно, сырье расходуется следующим образом:
200 кг ресурса авекс используется полностью;
120 кг ресурса бумакс используется полностью;
180 кг ресурса сидекс (250 - 70 кг (О);
150 кг ресурса Доракс используется полностью.
(Кроме того, объем производства химиката телтрейт составляет 350 кг (Е), что
ниже максимального спроса, равного 500 кг),
в) Двойственная модель:
Переменные модели:
Пусть А, В, С и D — стоимость 1 кг соответствующего сырья. Пусть Е —
стоимость спроса на 1 кг химиката телтрейт.
Заметим, что в данном случае те обозначения, которые использовались нами в
п б), имеют другое значения, но оба определения тесно связаны друг с другом.

556
Ответы авторов мод^а .„ ^^замеипишишые вопросы^
Целевая функция минимизирует общую стоимость используемого сырья и
стоимость спроса на телтрейт V, где-
V = 200А + 120В + 250С + 150D + 500Е ф. ст. в день.
В условиях соблюдения системы ограничений:
Доход от ростик: 0,4 А + 0,3 С + 0.3 D i 18,2 ф. ст. /кг
Доход от сеноупур: 0,4 А + 0,2 В + 0,3 С + 0,1 D г 14.2 ф. ст./кг
Доход от телтрейт: 0,4 В + 0,2 С + 0^4 D + Е г 23,8 ф. ст./кг
А, Б, С, D, Е ^0
Из нижней строки итоговой симплекс-таблицы получаем:
Стоимость 1 кг авекс, А = 15,6875 ф.ст
Стоимость 1 кг бумакс, В = 19,75 ф.ст
Стоимость 1 кг сидекс, С =
О
ф.ст
Стоимость 1 кг доракс, D = 39,75 ф. ст.
Стоимость спроса на телтрейт, Е = О ф. ст.
Подстановка данных значений переменных в целевую функцию дает мини-
мальное значение стоимости/цены V = 11470 ф. ст. в день.
г) Следует ли налаживать выпуск четвертого вида продукции упелин?
Каждый килограмм химиката упелин продавался бы по 50 ф.ст, а его произ-
водство потребовало бы 0,5 кг бумакса и 0,5 кг доракса. Единичный доход от
упелина равен:
50 - (0,5
X
25 + 0,5
X
20) = 27,5 ф. ст. за
1
кг.
Из решения двойственной задачи (или теневой цены) стоимость используемого
при производстве Упелина сырья составит:
0,5
X
19,75 + 0,5
X
39,75 = 29,75 ф. ст. за 1 кг.
Прюизводсгво 1 кг упелина требует использования сырья стоимостью 29,75 ф. ст.,
а отдача от него составляет 27,50 ф.ст, следовательно, выпуск этого продукта
налаживать не следует. Производство 1 кг упелина влечет за собой снижение
общего дохода на (29,75 - 27,5) = 2,25 ф. ст.
4.
а) (i) Определите ожидаемое значение ежегодного спроса:
Ожидаемое значение спроса в неделю =
= сумма (спроса за неделю) х вероятность =
= 20
X
0,1 + 30
X
0,6 + 40
X
0,3 = 32 шины в неделю.
Ожидаемое значение ежегодного спроса =
= 50 недель х ожидаемое значение спроса в неделю
= 50
X
32 = 1600 шин в год.
(ii) Определите вероятность того, что в течение трех недель поставки
заказа спрос превысит 100 единиц.
Существуют четыре возможных исхода, которые приводят к тому, что спрос
Превышает 100 единиц:

Отвь.пы авторов моделей на экзаменационные вопросы
557
F
Спрос за неделю
1 2 3
40+40+40
40+40+30
40+30+40
30+40+40
Итого
= 110
= 110
= 110
= 110
Вероятность
0,3
X
0,3
X
0,3 = 0,027
0,3x0,3x0,6 = 0,054
0,3x0,6x0,3 = 0,054
0,6x0,3x0,3 = 0,054
Итого 0,189
Общая вероятность того, что спрос больше 100 равен 0,189.
При проведении расчетов предполагалось, что значения спроса в течение
каждой недели не зависят друг от друга.
б) Использование простой формулы EOQ, чтобы доказать, что оптималь-
ный размер заказа равен 160.
Стоимость подачи заказа = С^ = 12 ф.ст за заказ.
Ожидаемый ежегодный спрос = D= 1600 шин в год.
Издержки хранения запаса = €„=0,15 х 10 = 1,50 ф. ст. в год.
EOQ
=
V
штг
4
2 • 1600
•
12
1,5
160 шин в одном заказе.
в) Построить имитационную 1>юдель движения запасов на 10-недельный
период и оценить общие издержки хранения sanacia в течение недели.
Начальный запас составляет 150 шин.
Размер заказа равен 160 шин.
Уровень повторного заказа равен 100 шин и включает в себя как
находящиеся в запасе, так и уже заказанные шины.
Поскольку ежедневный спрос нам неизвестен, будем исследовать только уровень
запаса, остающийся на конец недели. После этого будет подаваться новый заказ,
который будет получен через три недели, т.е. непосредственно перед началом
прюцесса торговли в течение следующей недели, например, заказ, поданный в конце
недели 4, прибудет непосредственно перед началом недели 8. Спрос, неудовлетво-
ренный из-за отсутствия запаса, по мере получения нового заказа не удовлетворяется.
Издержки, связанные с отсутствием запаса, равны 0,25 ф. ст. за шину.
Моделирование спроса осуществляется с помощью распределения нижеследу-
ющих случайных чисел в соответствии с вероятностями, указанными в п. а);
Спрос за неделю
20
30
40
Вероятность
0,1
0,6
0,3
Случайные числа, СЧ
0
1-6
7-^9
В течение десяти недель мы подадим два заказа, что будет стоить 2 х 12 = 24 ф. ст.
в неделю.
Средний уровень запаса на начало недели:
Средний уровень запаса на конец недели:
Следовательно, средний уровень запаса
составляет приблизительно
870/10 = 87 шин.
560/10 = 56 шин.
71,5 шин в неделю.
558
Ответы авторов моделей на
экзаменационные вопросы
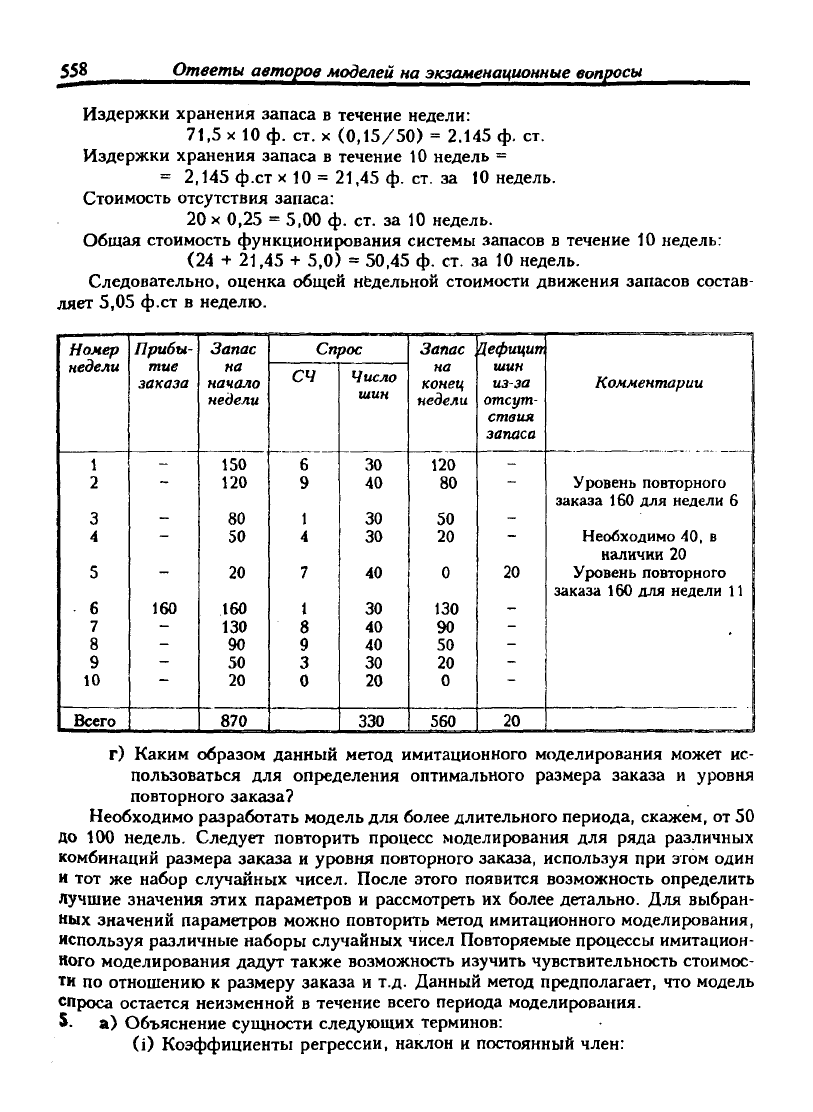
Издержки хранения запаса в течение недели:
71,5
X
10 ф. ст.
X
(0,15/50) = 2.145 ф. ст.
Издержки хранения запаса в течение 10 недель =
= 2,145
ф.стх
10 = 21,45 ф. ст. за 10 недель.
Стоимость отсутствия запаса:
20
X
0,25 = 5,00 ф. ст. за 10 недель.
Общая стоимость функционирования системы запасов в течение 10 недель:
(24 + 21,45 + 5,0) = 50,45 ф. ст. за 10 недель.
Следовательно, оценка общей недельной стоимости движения запасов состав-
ляет 5,05 ф.ст в неделю.
Номер
недели
1
2
3
4
5
6
7
8
9
10
Всего
Прибы-
тие
заказа
-
"
-
~
•"
160
-
-
-
~
Запас
на
начало
недели
150
120
80
50
20
160
130
90
50
20
870
Спрос
СЧ
6
9
1
4
7
1
8
9
3
0
Число
шин
30
40
30
30
40
30
40
40
30
20
330
Запас
на
конец
недели
120
80
50
20
0
130
90
50
20
0
560
Цефицип
шин
из-за
отсут-
ствия
запаса
-
—
-
~
20
-
-
-
-
~
20
Комментарии
Уровень повторного
заказа 160 для недели 6
Необходимо 40, в
наличии 20
Уровень повторного
заказа 160 для недели 11
г) Каким образом данный метод имитационного моделирования может ис-
пользоваться для определения оптимального размера заказа и уровня
повторного заказа?
Необходимо разработать модель для более длительного периода, скажем, от 50
до 100 недель. Следует повторить процесс моделирования для ряда различных
комбинаций размера заказа и уровня повторного заказа, используя при этом один
и тот же набор случайных чисел. После этого появится возможность определить
лучшие значения этих параметров и рассмотреть их более детально. Для выбран-
ных значений параметров можно повторить метод имитационного моделирования,
используя различные наборы случайных чисел Повторяемые процессы имитацион-
ного моделирования дадут также возможность изучить чувствительность стоимос-
ти по отношению к размеру заказа и т.д. Данный метод предполагает, что модель
спроса остается неизменной в течение всего периода моделирования.
S. а) Объяснение сущности следующих терминов:
(i) Коэффициенты регрессии, наклон и постоянный член:

Ответы .яторов моделей на экзаменационные
вопросы
^^9
Для оценки линейной связи между числом поданных заявок и ставкой процента по
закладным использовался пакет прикладных программ. Данная взаимосвязь имеет вид;
Число заявок, поданных в течение недели:
153,4
—
6,81
X
(% по закладным).
153,4 и -6,81
—
это коэффициенты регрессии.
Эмпирические значения ставки процента по закладным в течение 15 недель
изменяются от 10 до 15%. В рамках данного интервала модель позволяет рассчитать
оценку среднего количества заявок, которое можно ожидать в течение недели. Напри-
мер,
если бы ставка процента по закладным составляла 12%, оценка была бы равна:
количество заявок за неделю: 153,4 - 6,81 х 12 = 71,7, или 72.
Наклон линии регрессии равен -6,81 и означает, что при выходе за пршделы
указанного выше интервала увеличение ставки на 1% приведет к уменьшению
числа подаваемых заявок в среднем на 7 (6,81) единиц. Постоянный член 153,7 не
имеет определенного значения сам по себе. Его можно интерпретировать как
основное, или базисное значение, из которого мы вычитаем воздействие ставки
процента по закладным при выходе за определенный интервал ее значений.
(ii) Коэффициент детерминации.
Мы пытаемся объяснить, почему число заявок в неделю варьирует от 50 за 5-ю
неделю до 87 за 9-ю неделю. Для объяснения подобной вариации мы применяем
показатель ставки процента по закладным. Коэффициент детерминации является
мерюй, позволяющей установить, насколько хорошо данная вариация объясняется
с помощью регрессионной модели. Если коэффициеггг детерминации г равен 1,
нам удалось объяснить всю вариацию количества заявок на ссуды через взаимо-
связь со ставкой прюцента по закладным. В этом случае линейная модель является
идеальной. Если г равен О, вариация вообще не была объяснена, и модель
является непригодной к использованию.
Коэффициент детерминации: г = (-0,9721) = 0,945.
Данное значение достаточно близко к 1. Линейная модель хорошо объясняет
вариацию числа заявок на ссуды. Мы объяснили 94,5% вариации и не объяснили
оставшееся 5,5%.
(iii) Остаточное стандартное отклонение.
Мы уже установили, что построенная модель не является совершенной. Факти-
чески именно это и следовало предполагать, поскольку нам известно, что кроме
ставки прюцента по закладным спрюс на них подвержен воздействию и других
факторюв. Данные, собранные за 15 недель, наглядно демонстрируют это положение.
Так, для 3-й, 14-й и 15-й недель ставка по закладным составила
13%,
однако число
заявок было равно 62,65 и 61 соответственно. Если данная модель используется
для прюгнозирования числа поданных заявок при ставке по закладным в 13%,
полученное прогнозное значение окажется единственным и составит:
153,4 - 6,81
X
13) = 64,9 заявок.
Остаток — это разница между полученным по модели прогнозным и эмпири-
ческим значениями. В целом, остаточное стандартное отклонение представляет
собой оценку среднего отклонения между прогнозными и фактическими значениями.
Оно равно:
о =V
6,3349
= 2,517.
gjm Ответы авторов моделей на экзаменационные
вопросы
В среднем предполагается, что оценки содержат ошибку в две или три заявки.
Примечание: одна из предпосылок регрессионного анализа состоит в том, что
в генеральной совокупности значения у, соответствующие конкретным значениям х,
имеют нормальное распределение. Предполагается,
что
для всех х в этих нормальных
распределениях существует постоянное стандартное отклонение а^. Именно это
стандартное отклонение оценивается с помощью остаточного стандартного откло-
нения а (см. гл.8).
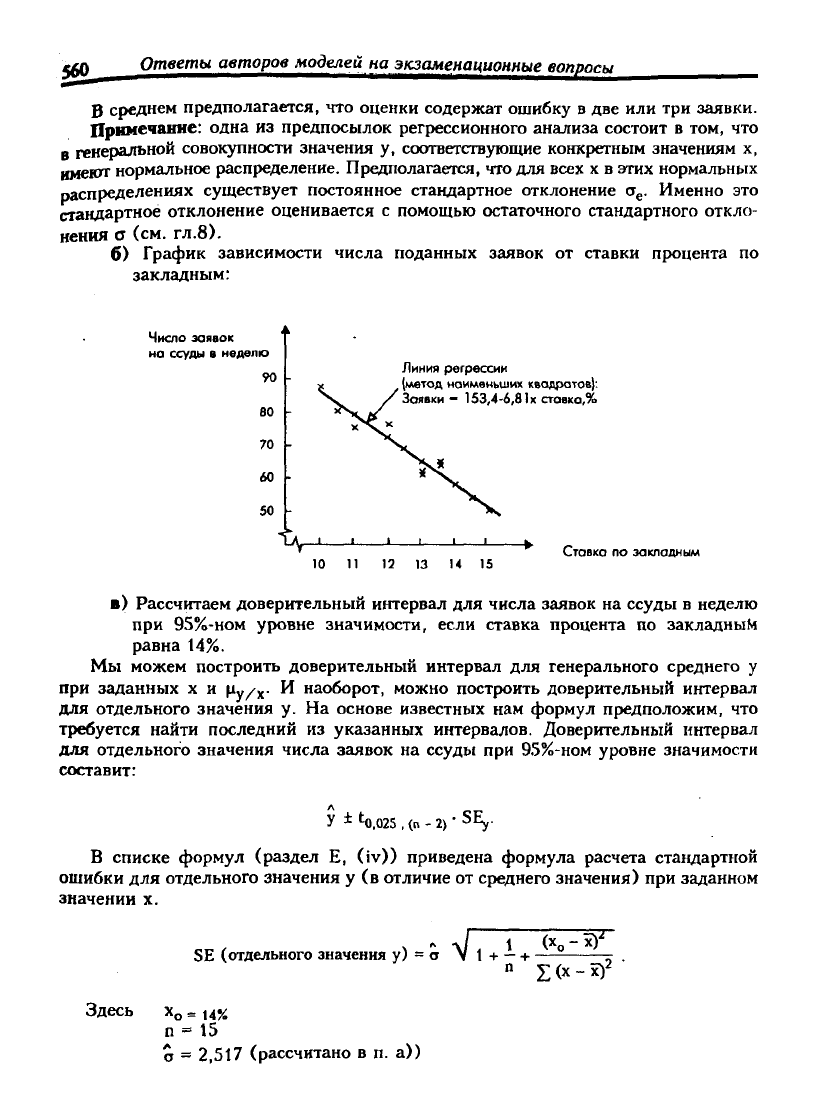
б) График зависимости числа поданных заявок от ставки процента по
закладным:
Число заявок
но ссуды в неделю
90
80
70
60
50
ч-
Линия регрессии
(метод наименьших квадратов):
Зоявки - 153,4-6,81X ставка,%
_1_
10 11 13 13 U 15
Ставка по закладным
в) Рассчитаем доверительный интервал для числа заявок на ссуды в неделю
при 95%-ном уровне значимости, если ставка процента по закладным
равна 14%.
Мы можем построить доверительный интервал для генерального среднего у
при заданных х и Цу/х- И наоборот, можно построить доверительный интервал
для отдельного значения у. На основе известных нам формул предположим, что
требуется найти последний из указанных интервалов. Доверительный интервал
для отдельного значения числа заявок на ссуды при 95%-ном уровне значимости
составит:
У =t '^0,025 , (п - 2) • SEy.
В списке формул (раздел Е, (iv)) приведена формула расчета стандартной
ошибки для отдельного значения у (в отличие от среднего значения) при заданном
значении х.
Здесь
SE (отдельного значения у)
14%
=^
vmrKHT.
п 5:
(X
-
50^
п= 15
а = 2,517 (рассчитано в п. а))

Ответы авторов моделей на экзаменационные
вопросы
561
X
= 12,5667 (дано по условию)
Ыо -
X
)2 = (14 - 12,5667)2 = 1,4333^ = 2,0543
SD (х) =
1,4744
(дано), следовательно,
Дисперсия (х) =
1,4744^
= 2,1739 =
(п-1)
, следовательно.
S(x -
X)'
Следовательно,
' = Дисперсия (х)
•
(п-1) = 2,1739
•
14 = 30,434.
Т
SE (отдельного значения у) = 2,517'V
1
+ -^ +
|Q7?7
= 2,517 х 1,065 = 2,68.
Прогнозное значение числа заявок на ссуды при
ставке по
закладным
в
14%
составит:
у = 153,4 - 6,81 • 14 = 58,06 заявок в неделю.
Доверительный интервал для отдельного значения числа заявок на ссуды при
95%-ном уровне значимости равен:
58,06 ± to
025
14
•
SE (отдельного значения у),
т.е.
58,06 ± 2,145 • 2,68 = 58,06 ± 5,75,
т.е.
от 52,3 до 63,8 заявок в неделю.
Данный результат можно сравнить с числом заявок на ссуды, поданными в
течение 6-й недели и равными 58, при ставке по закладным в 14%.
6. а) Найдем среднее значение и стандартное отклонение продолжительности
выполнения каждой задачи. Используя указанные формулы
(4т
+
а
+ Ь) (Ь
- а)
получим:
Задача
А
В
С
D
Е
F
G
Н
I
J
К
Предшествующая
задача
-
-
А
В
D,A
В
C,E,F
G
G
Н
I,J
m
3
12
5
4
3
4
10
3
2
5
4
Продолжительность
а
2
10
4
2
3
3
8
2
2
4
2
Ь
4
20
12
6
3
5
18
4
2
6
12
М
3
13
6
4
3
4
И
3
2
5
5
а
2/6
10/6
8/6
4/6
0
2/6
10/6
2/6
0
2/6
10/6
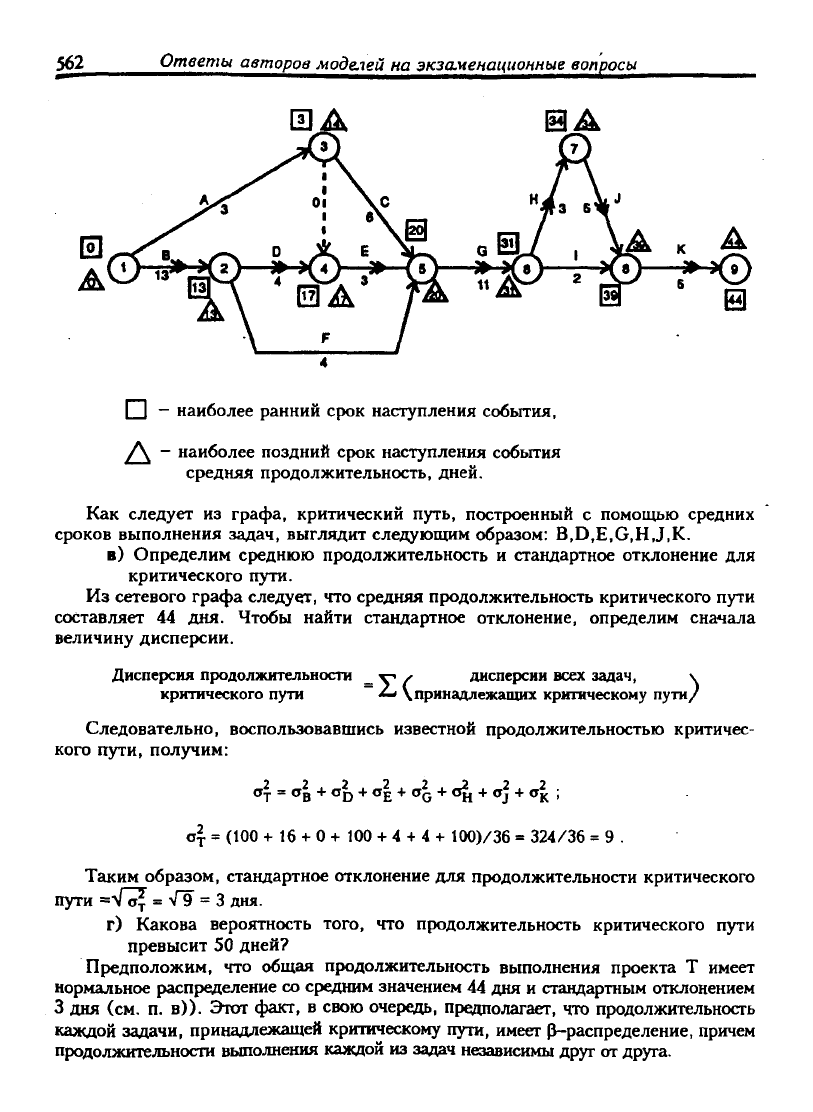
б) Построим сетевой граф и определим критический путь (см. с. 563)
Сетевой граф приведен ниже. Наиболее ранние и наиболее поздние сроки
наступления событий указаны около соответствующих узлов. Задача является
критической, если ЬЕТ^ - EET„j,,3j,a - продолжительность = 0.
562
Ответы авторов моделей на экзаменационные вопросы
I I - наиболее ранний срок наступления события,
/\ - наиболее поздний срок наступления события
средняя продолжительность, дней.
Как следует из графа, критический путь, пострюенный с помощью средних
сроков выполнения задач, выглядит следующим образом: B,D,E,G,H,J,K.
в) Определим среднюю продолжительность и стандартное отклонение для
критического пути.
Из сетевого графа следует, что средняя продолжительность критического пути
составляет 44 дня. Чтобы найти стандартное отклонение, определим сначала
величину дисперсии.
Дисперсия продолжительности
критического пути
Z
/ дисперсии всех задач, \
\ принадлежащих критическому пути/
Следовательно, воспользовавщись известной продолжительностью критичес-
кого пути, получим:
а.,. = Од + oj)
+
og
+
Од + Оц + aj + Ок ;
а\ = (100 + 16 +
О
+ 100 + 4 + 4 + 100)/36 = 324/36 = 9 .
Таким образом, стандартное отклонение для продолжительности критического
пути =V^ = VT = 3 дня.
г) Какова вероятность того, что продолжительность критического пути
превысит 50 дней?
Предположим, что общая продолжительность выполнения проекта Т имеет
нормальное распределение со средним значением 44 дня и стандартным отклонением
3 дня (см. п. в)). Этот факт, в свою очередь, предполагает, что продолжительность
каждой задачи, принадлежащей критическому пути, имеет р-распределение, причем
продолжительности выполнения каждой из задач независимы друг от друга.

Ответы
авторов моделей
на экзаменационные
вопросы
563
<т
= 3 дня
44 50
-• Т, дней
50 дней составляют z стандартных отклонений от среднего значения, равного
44 дням, где:
50-44 „-
z = —3—= 2.0.
По таблице стандартного нормального распределения находим, что Р (z > 2,0)
= 0,02275. Следовательно, вероятность того, что продолжительность критического
пути превысит 50 дней, равна 0,02275.
7.
а) Рассчитаем доверительный интервал для выработки за
1
чел.-ч. в целом при
95%-ном уровне значимости в условиях новой структуры заработной платы.
Предпосылки:
1.
Для каждого завода можно вычислить соответствующий показатель нормы
выработки, т.е. в течение рассматриваемого временного промежутка каждый
завод выпускает только один продукт или по крайней мере имеет постоянный
ассортимент продукции.
2.
Показатели нормы выработки для различных заводов сопоставимы, т.е. все
заводы производят сходные виды продукции.
3.
Показатели нормы выработки по всем заводам подчиняются нормальному
закону распределения и имеют одинаковые среднее значение и стандартное
отклонение.
Для новой структуры заработной платы имеем:
п = 8,
зё =
50,
5
= 10,344.
Доверительный интервал для нормы выработки как генерального среднего при
95%-ном уровне значимости равен:
X
±
to 025,7
s/V (n - 1) = 50 ± 2,365
X
10,344/^7 = 50 ± 9,246.
Мы можем бьггь на 95% уверены, что норма выработки как генеральное
среднее лежит в пределах между 40,754 и 59,246.
6) (i) Почему попарный t-критерий являлся бы неподходящим инструмен-
том при проверке предположения о том, что изменение в структуре
заработной платы не привело к изменениям в норме выработки в целом?
Две выборки не являются попарно сопоставимыми. Они получены на основе
различных заводов до и после изменения структуры заработной платы. Если бы
прюводилась выборка 8 заводов, по которым показатели выработки фиксирова-

^64 Ответы авторов моделей на экзаменационные
вопросы
лись бы до и после изменения структуры заработной платы, попарный t-критер
можно было бы использовать.
(ii) Будем использовать t-критерий для средних значений двух выборок.
Примечание. Данной процедуре должен предшествовать F-критерий для reh
ральных дисперсий. Предположим, что обе выборки были получены из генеральн!
совокупностей, имеющих равные дисперсии. Если сравнить приведенные ни>
стандартные отклонения двух выборок, сделанное нами предположение мож1
считать вполне допустимым (и фактически F-критерий это подтверждает). Нал
также предполагается, что лежащие в основе выборок генеральные совокупное-
распределены нормально.
HQ:
ji(, =
HN.
различие в нормах выработки при старой и новой структур;
заработной платы отсутствует.
Н):
Но
5*
HN,
различие в нормах выработки существует.
Формулировка гипотезы Hj предполагает использование двухвершинно!
критерия. (Если бы зтверждалось, что новая структура была введена в целя
увеличения выработки, то в этом случае гипотеза Н] формулировалась бы следз
ющим образом: Hj: ц^ < ц^ . и можно было бы применять одновершинный критерш
Из постановки проблемы не ясно, действительно ли преследовалась именно эт
цель,
однако обе выборки идут в размер с данной идеей, поскольку средняя норм
выборки снизилась с 55 до 50)
Проведем проверку гипотезы HQ, используя двухсторонний t-критерий, н
5%-ном
уровне значимости (п^ + nj - 2) = (8 + 8 -2) = 14 степеней свободы.
По таблицам стандартного t-распределения находим, что
Чо25,14 = 2,145.
Необходимо знать выборочные средние и стандартные отклонения.
Для старой структуры заработной платы:
HQ
= 8,
XJ,
= 55
И
SQ
= 11,916.
Для новой структуры заработной платы:
Пк
= 8,
Хц
= 50 и
SN
= 11,916.
Значение t-критерия равно:
. _ ^о ^N
л
SE
Следовательно,
55-50
л/("о
SQ^
+
"N
О 1 1~ л/(8 •11.916''+
8.10,344^)
1 1
(п„
+
п„-2) Ч*п« (8
+
8-2) ^8 + 8'
Jlt)91,9'i " Ш^
и-А
0,838.
Так как
0,838
< too25 14~ 2,145 результат не является значимым на
5%-ном
уровне. Выборка подтверждает гипотезу HQ, поэтому
HQ
принимается. Мы не
находим доказательства в поддержку того, что изменения в выработке действи-
тельно имели место.
(Hi) Почему для таких данных желательно использовать тест, не предпола-
гающий какого-либо конкретного распределения элементов coBoKvnHrv-rH"?
