Эддоус М., Стэнсфилд Р. Методы принятия решений
Подождите немного. Документ загружается.


Гл.
8. Линейная
регрессия
283
Требуется:
1.
Изобразить данные на графике. Измерить тесноту линейной связи.
2.
Построить модель регрессии и вычислить коэффициенты.
3.
Какие еще факторы вы предлагаете рассмотреть?
Упражнение 8.3
Туристическую фирму крупного курортного города интересует связь между чис-
лом отпускников, останавливающихся в отелях и расходами на рюкламу отелей.
Взято случайное число отелей
—
6, сходных по размеру. Была собрана следующая
информация за текущий сезон:
Отель
Реклама, ф. ст.
Число гостей
1
9000
1100
2
6000
1200
3
10000
1600
4
8000
1300
5
7000
1100
6
4000
800
Требуется:
1.
Построить модель для объяснения изменения числа гостей и проверить досто-
верность этой модели.
2.
Прокомментировать точность прогнозов, производимых по этой модели.
Упражнение 8.4
/1ля установления стандартных издержек бухгалтер фирмы собрал следующие данные:
Выпуск,
тыс.
ед. в день
Издержки,
тыс.
ф. ст.
за день
12
3.2
19
4.1
12
2.9
17
3,8
15
3.6
15
3.5
17
3,9
16
3.7
18
4.0
19
4,2
Требуется:
1.
Установить предварительные стандарты.
2.
Прокомментировать, насколько точна оценка стандартных издержек. Какие
факторы могут быть дополнительно включены в стандарты для увеличения
точности?
Упражнение 8.5
Компания "Garden Groceries" владеет 12 магазинами. Размер размещенных мага-
зинов велик. Финансовый директор группы магазинов рассматривает возможность
слияния числа мелких магазинов для увеличения прибыльности компании. Он
предположил, что оборот магазинов вследствие слияния останется прежним. Ему
необходимо установить связь между прибылью и оборотом. Данные для каждого
магазина в отдельности за последний финансовый год приведены ниже:

284
4.2. Анализ данных как
составная
часть принятия решений
Магазин
1
2
3
4
5
6
7
8
9
10
И
12
Годовая прибыль.
тыс.
ф. ст.
2
4
И
17
18
28
34
36
48
55
71
85
Оборот,
тыс.
ф. ст.
50
60
85
85
100
120
140
155
180
210
250
300
2.
Требуется:
Построить модель для описания связи между прибылью и оборотом. Интерпре-
тировать каждую постоянную данной модели. Прокомментировать примени-
мость модели.
Дать советы финансовому директору по поводу слияния магазинов.
Упражнение 8.6
15 студентов сдали экзамены по бухгалтерскому учету и математике. Их ранжиро-
вание по итогам экзаменов дано ниже. Существует ли какая-нибудь связь между
этими двумя результатами?
Студент
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
Бухгалтерский
учет
10
5
12
1
6
2
7
И
15
3
9
14
13
4
8
Математика
13
4
10
1
И
2
8
9
14
5
7
12
15
3
6
Упражнение 8.7
Компания имеет большое количество продавцов, которые предъявили отчеты о
своих поездках. Десять из них предъявили требования на оплату этих поездок.
За два квартала компания выплатила 17,5 пенсов за каждую милю проезда.

Гл.
8. Линейная
регрессия
285
Продавец
А
Б
В
Г
Д
Е
Ж
3
И
к
пройдено миль
в I квартале
28
26
35
20
30
16
40
36
24
25
Пройдено
миль
во II квартале
45
54
49
36
50
32
64
56
44
50
Требуется:
1.
Не используя данные за I квартал, найти: вычисленное значение, доверительный
интервал при
95%
веро5гп10сти для среднего уровня расходов на поездку каждого
продавца, который должен быть выплачен во II квартале.
2.
Определить линию регрессии методом наименьших квадратов, с помощью
которой можно предсказать пройденные мили во II квартале, за базис принять
количество миль, пройденных в I квартале.
Среднее расстояние, пройденное продавцом за i квартал, равно 3000 миль.
С помощью полученного уравнения регрессии рассчитайте значение средних
расходов каждого продавца за П квартал.
Какое из двух полученных значений вы бы рекомендовали использовать?
Почему?
Упражнение 8.8
Главный бухгалтер "Реп Prqdakts" проанализировал время, затраченное на произ-
водство основных продуктов компании. Он получил следующие данные для
одного конкретного продукта, который производился на серийной основе:
Серия
продуктов
1
2
3
4
5
6
7
8
9
10
Размер серии
продуктов
32
24
30
45
15
26
50
18
20
40
Время, ч
21,4
17,0
20,4
29,6
12,6
19,1
34,2
15,2
16,3
29.2
Данные расположены в хронологическом порядке по времени производства
серии каждого типа предметов за прошедший год. Получив эти данные, бухгалтер
построил уравнение регрессии для связи между временем у и размером серии х.

286
4.2. Анапиз данных как составная часть
принятия
решений
у = 3,5 + 0,6х
с коэффициентом корреляции 0,99. Учитывая высокую корреляцию, бухгалтер
заключил, что размер серии является "предсказателем" величины затраченного
времени.
Требуется:
1.
Объяснить полученные значения коэффициентов регрессии в контексте данного
примера.
2.
Вычислить отклонения рассматриваемого производственного времени от линии
регрессии и показать, что эти отклонения в сумме равны нулю. Объяснить,
почему они всегда будут в сумме стремиться к нулю.
3.
Вычислить сумму квадратов отклонений и объяснить важность полученных
значений.
4.
Изобразить на графике отклонения в связи с размером серии продуктов и
номером серий. Какой вывод вы можете сделать из пол)гченного графика?
Согласны ли вы с мнением, что размер партии товара является величиной, с
помощью которой можно точно предсказать время?
Упражнение 8.9
"Pandora" — включает региональною распределенную систему с большим числом
товарных вагонов, прикрепленных к определенным семи складам. Когда на
каждую поставку был определен свой склад и конкретный день поставки, каждому
поставщику соотвегсгвовала определенная группа потребителей. Поставщик постав-
ляет со склада картон каждо!^ потребителю, следуюпдай определенным маршрутом.
Определите эффекгавность системы распределения, используя следующие данные:
Группа
поставщиков
1
2
3
4
5
6
Затраченное
время, ч
6,3
4,7
5,0
8.5
3,8
4.1
Число
потребителей
6
3
4
7
4
6
Общий
вес груза
(картон),
т
24
15
17
30
14
20
Требуется:
1.
Изобразить данные в удобной форме и прокомментировать появившиеся связи.
2.
Определить коэффициент корреляции Пирсона между величинами времени и
каждой из оставшихся переменных. Прокомментируйте эти две переменные как
величины, помогающие предсказать общее время поставки.
3.
Если регрессия для общего время поставки включает число потребителей и
величину общего веса груза, то получен коэффициент множественной корреля-
ции, равшлй 0,99. Объясните значение этой величины и сравните ее с двумя
парными коэффициентами корреляции, которые вы определили в п. 2.
Гл.
8. Линейная
регрессия
287
Упражнение 8.10
Компания "Themis Processing Ltd", полностью подчиненная компании "Tantalus
Products", была основана в 19X6 г. для добычи железной руды. С той поры
"Themis" построил 10 новых фирм, строящих заводы различных размеров, кото-
рые успешно функционируют и получают немалую прибыль. В настоящее время
эта компания рассматривает перспективу построения двух дополнительных заво-
дов.
Так как средние производственные издержки — это критический фактор в
общей прибыльности предприятия, важно оценить будущие издержки на ранних
стадиях прюизводства.
Главный бухгалтер полагает, что некоторые из ключевых факторов влияют на
производственные издержки и это такие факторы как: экономия масштаба, они
присутствуют на заводах различных размеров. Чтобы доказать свою точку зрения,
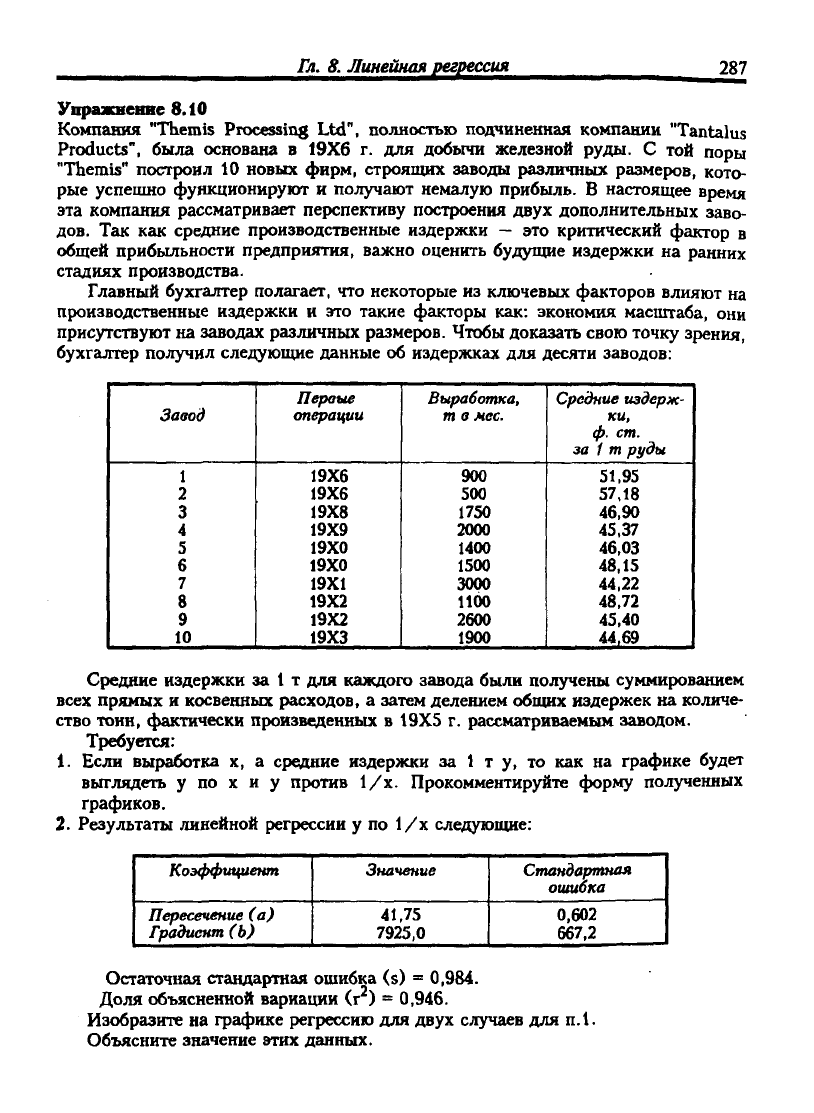
бухгалтер получил следующие данные об издержках для десяти заводов:
Завод
1
2
3
4
5
6
7
8
9
10
Первые
операции
19X6
19X6
19X8
19X9
19X0
19X0
19X1
19X2
19X2
19X3
Выработка,
т в
мае.
900
500
1750
2000
1400
1500
3000
1100
2600
1900
Средние
издерж-
ки,
ф. ст.
за 1 т руды
51,95
57,18
46,90
45,37
46,03
48,15
44,22
48,72
45,40
44,69
Средние издержки за 1 т для каждого завода были получены суммированием
всех прямых и косвенных расходов, а затем делением общих издержек на количе-
ство тонн, фактически произведенных в 19X5 г. рассматриваемым заводом.
Требуется:
1.
Если выработка х, а средние издержки за 1 ту, то как на графике будет
выглядеть у по X и у против 1/х. Прокомментируйте форму полученных
графиков.
2.
Результаты линейной регрессии у по 1/х следующие:
Коэффициент
Пересечение
(а)
Градиент
(Ь)
Значение
41,75
7925,0
Стандартная
ошибка
0,602
667,2
Остаточная стандартная ошибка (s) = 0,984.
Доля объясненной вариации (г ) =
0,946
Изобразите на графике регрессию для двух случаев для п.1.
Объясните значение этих данных.

288 4.2. Анализ данных как составная
часть
принятия решений
3.
На диаграмме для у по
1
/х укажите 95%-ые пределы на основе остаточной
стандартной ошибки. Объясните, почему эти пределы нахождения величины
ошибки не обеспечивают прогноз доверительных интервалов при прогнози-
ровании средних издержек на 1 т для данного значения 1/х.
Упражнение 8.11
Применение внутренней электрической системы было вынесено на внешний рынок
в 1982 г. Покупателям была предоставлена возможность купить страховой полис
для покрытия затрат на ремонт на 5 лет. Таблица внизу показывает общий объем
продаж лицензии за 1982-1988 гг. вместе с продажей страховых полисов и с
учетом общего индекса це.н на товары электрической промышленности.
Год
1982
"
1983
1984
1985
1986
1987
1988
Продажа
лицензий,
тыс. ф. ст.
3600
6250
9170
14000
21600
27000
41600
Продажа
полисов,
ед
400
300
600
1200
1700
2200
2000
Индекс
цен
120
126
131
140
144
150
160
1.
Объясните, почему важно установить первоначальные объемы продаж лицензии
при инфляции, когда проявляется связь между объемом продаж лицензий на
применение и числом проданных страховых полисов. Сопоставьте с ценами
1980 г.
2.
Вычислите коэффициент детерминации между дефлированным уровнем продаж
лицензий и числом страховых полисов, объяснить полученный результат.
3.
Вычислите уравнение линейной регрессии с помощью метода наименьших
квадратов для прогноза количества проданных полисов при данном дефлиро-
ванном уровне продаж лицензий.
4.
Общие продажи лицензии в 1989 г. оценивались в
51
млн. ф. ст. в ценах 1989 г.; в
1989 г. индекс цен на электротехнические товары к ценам 1980 г. должен равняться
170.
Предскажите продажи страховых полисов в 1989 г. с помощью регрессионного
анализа,
5.
Прокомментируйте недостатки использования данного типа исследования для
прогноза продаж полисов в 1989 г.
Упражнение 8.12
Компания "Venus Tableware Ltd" является основным производителем керамичес-
кой посуды в Блюленде. Сумма импорта и экспорта керамических изделий
незначима по сравнению с местным объемом производства. Таким образом можно
Гл.
8. Линейная
регрессия
289
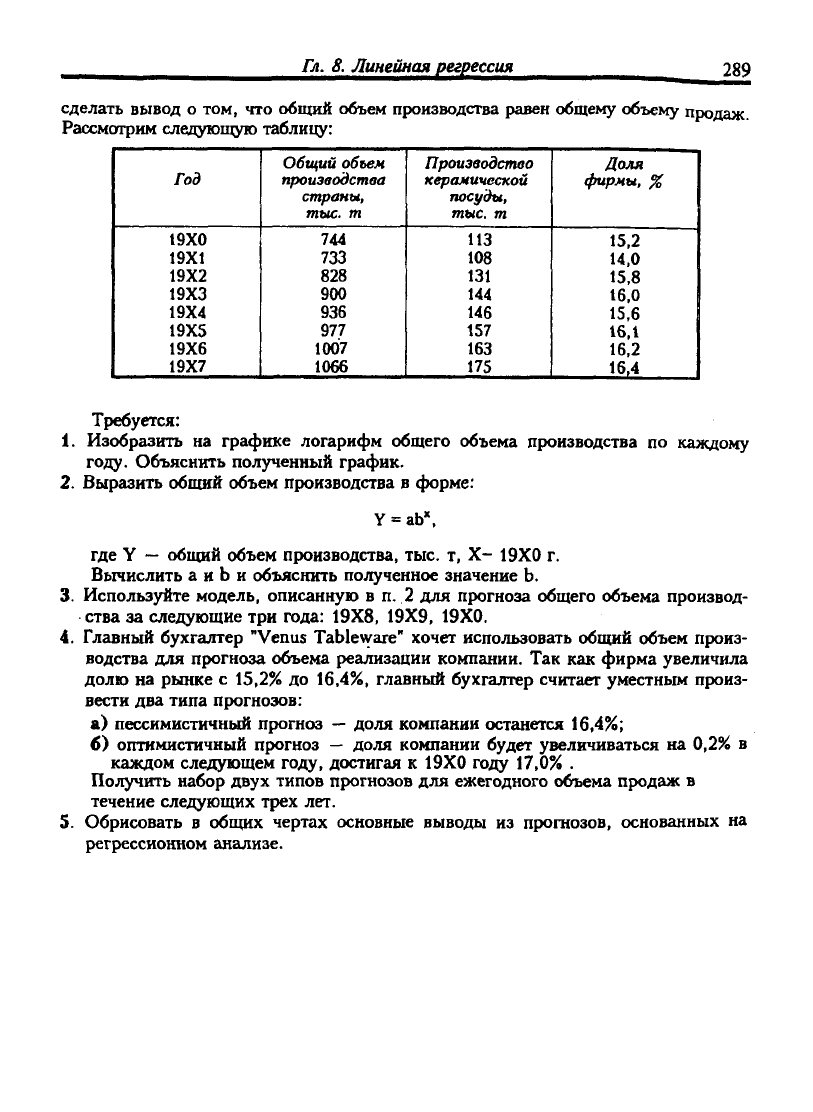
сделать вывод о том, что общий объем производства равен общему объему продаж
Рассмотрим следующую таблицу:
Год
19X0
19X1
19X2
19X3
19X4
19X5
19X6
19X7
Общий объем
производства
страны,
mtuc.
т
744
733
828
900
936
977
1007
1066
Производство
керамической
посуды,
тыс.
т
ИЗ
108
131
144
146
157
163
175
Доля
фирмы, %
15,2
14.0
15,8
16,0
15,6
16,1
16,2
16,4
Требуется:
1.
Изобразить на графике логарифм общего объема производства по каждому
году. Объяснить полученный график.
2.
Выразить общий объем производства в форме:
Y =
аЬ*.
где Y
—
общий объем производства, тыс. т, Х- 19X0 г.
Вычислить а и Ь и объяснить полученное значение Ь.
3.
Используйте модель, описанную в п. 2 для прогноза общего объема производ-
ства за следующие три года: 19X8, 19X9, 19X0.
4.
Главный бухгалтер "Venus ТаЫе>уаге" хочет использовать общий объем произ-
водства для прогноза объема реализации компании. Так как фирма увеличила
долю на рынке с 15,2% до 16,4%, главный бухгалтер считает уместным произ-
вести два типа прогнозов:
а) пессимистичный прогноз
—
доля компании останется 16,4%;
б) оптимистичный прогноз — доля компании будет увеличиваться на 0,2% в
каждом следующем году, достигая к 19X0 году 17,0% .
Получить набор двух типов прогнозов для ежегодного объема продаж в
течение следующих трех лет.
5.
Обрисовать в общих чертах основные выводы из прогнозов, основанных на
регрессионном анализе.

290
Глава 9. ВРЕМЕННЫЕ РЯДЫ
И ПРОГНОЗИРОВАНИЕ
9.1.
ВВЕДЕНИЕ
Каким бы видом бизнеса вы ни занимались, вам приходится планировать предпри
нимательскую деятельность на будущий период. При составлении как краткосроч
ных, так и долгосрочных планов менеджеры вынуждены прогнозировать будущие
значения таких важнейпгах показателей, как, например, объем продаж, ставки
процента, издержки и т.д. В этой главе мы рассмотрим возможности применения
в целях прогнозирования фактических данных за прошлые промежутки времени.
В предыдущей главе при характеристике регрессионных методов колебания
зависимой переменной объяснялись на основе изучения соответствующих значе-
ний независимой переменной. В данной главе мы будем использовать аналогичный
подход, причем в качестве независимой будет выступать переменная времени. К
примеру, мы хотим объяснить колебания объемов продаж только через изменение
значений этого показателя во времени, без учета каких-либо других факторов.
Если удается выявить определенную тенденцию изменения фактических значений,
то ее можно использовать для прогнозирования будущих значений данного пока-
зателя. Множество данных, в которых время является независимой переменной,
называется временным рядом.
Модель, построенную по ретроспективным данным, не всегда можно использо-
вать в прогнозировании отдельных показателей. Например, план некоторой ком-
пании может коренным образом измениться, если эта компания несет убытки.
Кроме того, существует множество внешних факторов, которые могут полностью
изменить тенденцию, существовавшую ранее. К таким факторам можно отнести
существенные изменения цен на сырье, резкое увеличение уровня инфляции в
мире в целом или стихийные бедствия, которые непредсказуемым образом могут
повлиять на предпринимательскую деятельность.
В разделе 9.2 мы р>ассмотрим В1>емениые ряды, которые содержат такие
элементы, как собственно тренд, сезонная вариация и циклическая вариация. Эти
элементы можно объединять с помощью нескольких способов. Остановимся на
двух тип&х моделей: модели с аддитивной компонентой и модели с мультипли-
**пшвой компонентой. Как следует из их названий, элементы в этих моделях
явбо складываются друг с другом, либо перемножаются. Каждой из моделей
'•''гветствуют различные методы расчета компоненты тренда. Мы будем исполь-
•овать сочетание методов скользящего среднего и линейной регрессии.

Гл.
9. Временные ряды и прогнозирование
291
Следует иметь в виду, что описанные выше методы — это далеко не весь, а
иногда и не лучший инструментарий для составления прогнозов. Существует
множество других, более изощренных статистических методов. Помимо количест-
венных, существуют также качественные методы, которые используются в услови-
ях недостаточного количества или отсутствия фактических данных. Среди них
можно назвать, например, метод Дельфи, который используется экспертами для
прогнозирования возможных будущих последствий, и метод написания сценария.
9.2.
ЭЛЕМЕНТЫ ВРЕМЕННОГО РЯДА
Значения некоторой переменной (например, объемы продаж) изменяются во
времени под воздействием целого ряда факторов. Если, к примеру, некоторая
компания предлагает на рынке новый вид продукции, то с течением времени
объемы продаж этой продукшш возрастают. Общее изменение значений переменной
во времени называется трендом и обозначается через Т. В примерах, которые будут
рассмотрены ниже, тренд является линейным. Это означает, что модель тренда
легко построить, используя для расчета пар)аметров прямой, наилучшим образом
аппроксимирующий данный тренд, метод регрессии. Затем данная модель может
использоваться для прогнозирования будущих значений тренда. В действитель-
ности тренд в чистом виде либо не существует, например, при колебании значений
спроса вокруг некоторой фиксированной величины, либо в большинстве случаев он
является нелинейным. На приведенных ниже рис. 9.1 и 9.2 проиллюстрирован тренд
значений спроса в соответствии с различными стадиями жизненного цикла продукта.
Новым видам продукции соответствует возрастающий тренд, тогда как устаревшим
продуктам на заключительной стадии их жизненного цикла — убывающий.
Метод скользящего среднего, изложенный ниже, можно использовать для
выделения тртнда из модели, содержащей сезонную компоненту. Этот метод
позволяет выравнивать тренд фактических значений через сглаживание сезонных
колебаний. Однако тренды, полученные с использованием метода скользящего
среднего, как правило, не используются для прогнозирования будущих значений,
поскольку процесс их получения предполагает высокий уровень неопределенности.
Время
Рис. 9.1. Объемы продаж новой продукции, пользующейся спросом
292
¥. 2. Анализ данных как составная часть принятия решений
Время
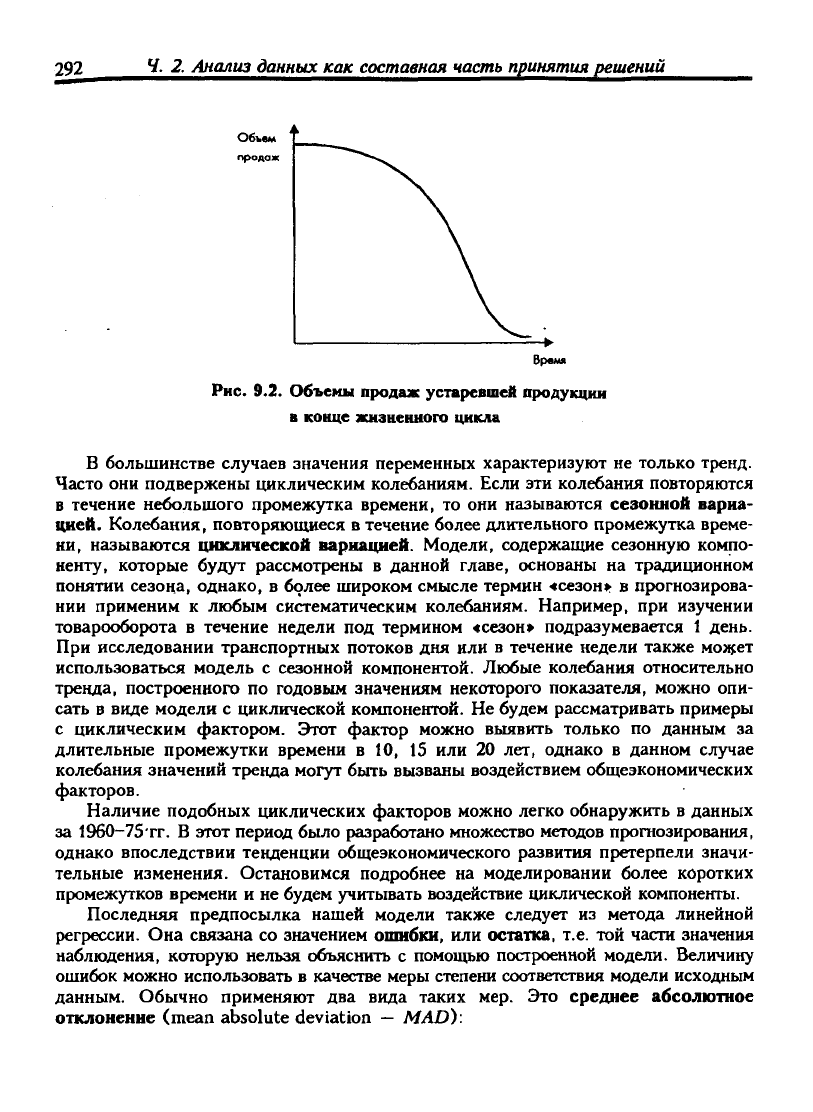
Рис.
9.2. Объемы продаж устаревшей продукции
в конце жизненного цикла
В большинстве случаев значения переменных характеризуют не только тренд.
Часто они подвержены циклическим колебаниям. Если эти колебания повторяются
в течение небольшого промежутка времени, то они называются сезонной вариа-
цией. Колебания, повторяющиеся в течение более длительного промежутка време-
ни,
называются циклической вариацией. Модели, содержащие сезонную компо-
ненту, которые будут рассмотрены в данной главе, основаны на традиционном
понятии сезона, однако, в более широком смысле термин 4сезон% в прогнозирова-
нии применим к любым систематическим колебаниям. Например, при изучении
товарооборота в течение недели под термином «сезон» подразумевается 1 день.
При исследовании транспортных потоков дня или в течение недели также моя?ет
использоваться модель с сезонкой компонентой. Любые колебания относительно
тренда, построенного по годовым значениям некоторого показателя, можно опи-
сать в виде модели с циклической компонентой. Не будем рассматривать примеры
с циклическим фактором. Этот фактор можно выявить только по данным за
длительные промежутки времени в 10, 15 или 20 лет, однако в данном случае
колебания значений тренда могут быть вызваны воздействием общеэкономических
факторов.
Наличие подобных циклических факторов можно легко обнаружить в данных
за 1960-75'гг. В этот период было разработано множество методов прогнозирования,
однако впоследствии тенденции общеэкономического развития претерпели значи-
тельные изменения. Остановимся подробнее на моделировании более коротких
промежутков времени и не будем учитывать воздействие циклической компоненты.
Последняя предпосылка нашей модели также следует из метода линейной
регрессии. Она связана со значением ошибки, или остатка, т.е. той части значения
наблюдения, которую нельзя объяснить с помощью построенной модели. Величину
ошибок можно использовать в качестве меры степени соответствия модели исходным
данным. Обычно применяют два вида таких мер. Это среднее абсолютное
отклонение (mean absolute deviation
—
MAD):
