Эддоус М., Стэнсфилд Р. Методы принятия решений

Подождите немного. Документ загружается.

Гл.

8. Линейная регрессия

253

Таблица 8.3. Расчет остатжов (у-у)

Расстояние,

миль

3,5

2,4

4.9

4,2

3,0

1,3

1,0

3.0

1,5

4,1

Фактическое

время, мин

Вычисленное

время

у =

5.91+2.66Х,

мин,

15,22

12,29

18,94

17,08

13,89

9.37

8,57

13,89

9,90

16,82

Остаток

е=(у-у),

мин

+0,78

+0,71

+0,06

+0,92

-1,89

+1,63

-0,57

+0,11

-0,90

-0,82

Мы можем проверить удовлетворительность модели, нанося остатки (у-у) на

ось ординат против вычисленных значений у, с учетом значений х. Эта процедура

очень важна при построении множественной регрессии, когда исходные данные не

могут быть нанесены на исходную диаграмму, т.е. линейность предположенной

связи может быть оценена в полной мере только через анализ остатков. Если

линейная модель является точной, разности, или остатки, будут носить случайный

характер и их сумма будет близка к нулю. Изображение разностей, или остатков,

для данного примера дано на рис. 8.10.

Остот(ж,мин

2 -

1 -

• -(У-у)

-2 -

1—

—г-

20 Оценка >ремени поездки у, *шн.

Рис. 8.10. График остатке» (у-у) пропш вычнеденных вначеянй у

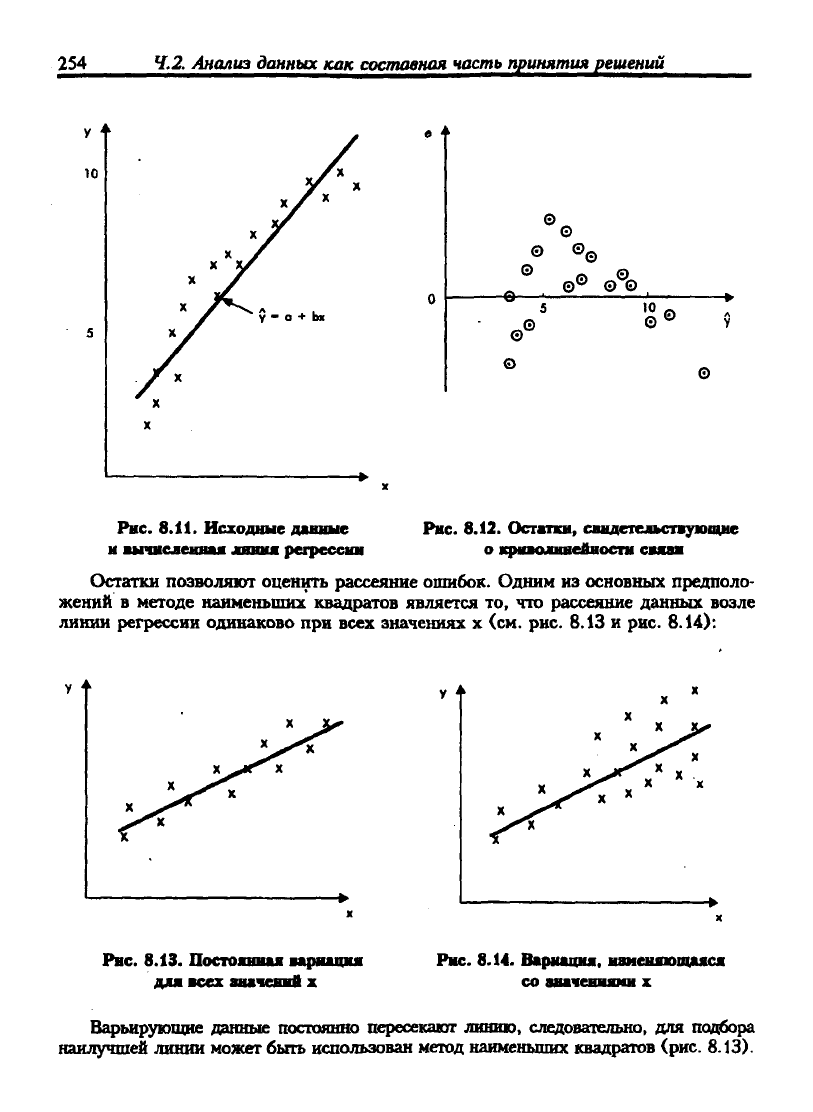
Если бы связь была нелинейной, то рисунок показал бы это очень четко.

Пример эффекта линейной модели показан на рис. 8.11 и 8.12.

254 4.2. Анализ данных как составная часть принятия решений

®0

00 0®о

Рнс. 8.11. Исходные давные

н внчнсленваж лшкя регресснн

Рнс. 8.12. Остжпсн, свидетельствующие

о |д>ивоип1нгйиостн свявв

Остатки позволяют оценить рассеяние ошибок. Одним из основных предполо-

жений в методе наименьших квадратов является то, что рассеяние данных возле

линии регрессии одинаково при всех значениях х (см. рис. 8.13 и рис. 8.14):

Рнс. 8.13. Постоянная мршння

для всех «шчеввй X

Рнс. 8.14. Вартцня, ввиешоощшяся

со авачешиошх

Вгфьирующие данные постоянно пересекают линию, следовательно, для noiO^opa

наилучшей линии может быть использован метод наименьших квадратов (рис. 8.13).

Гл.

8. Линейная регрессия

255

На рис. 8.14 показан пример данных, которые распределяются вдоль линии

регрессии неравномерно, в этом случае метод наименьших квадратов непригоден

для подбора "наилучшей" линии.

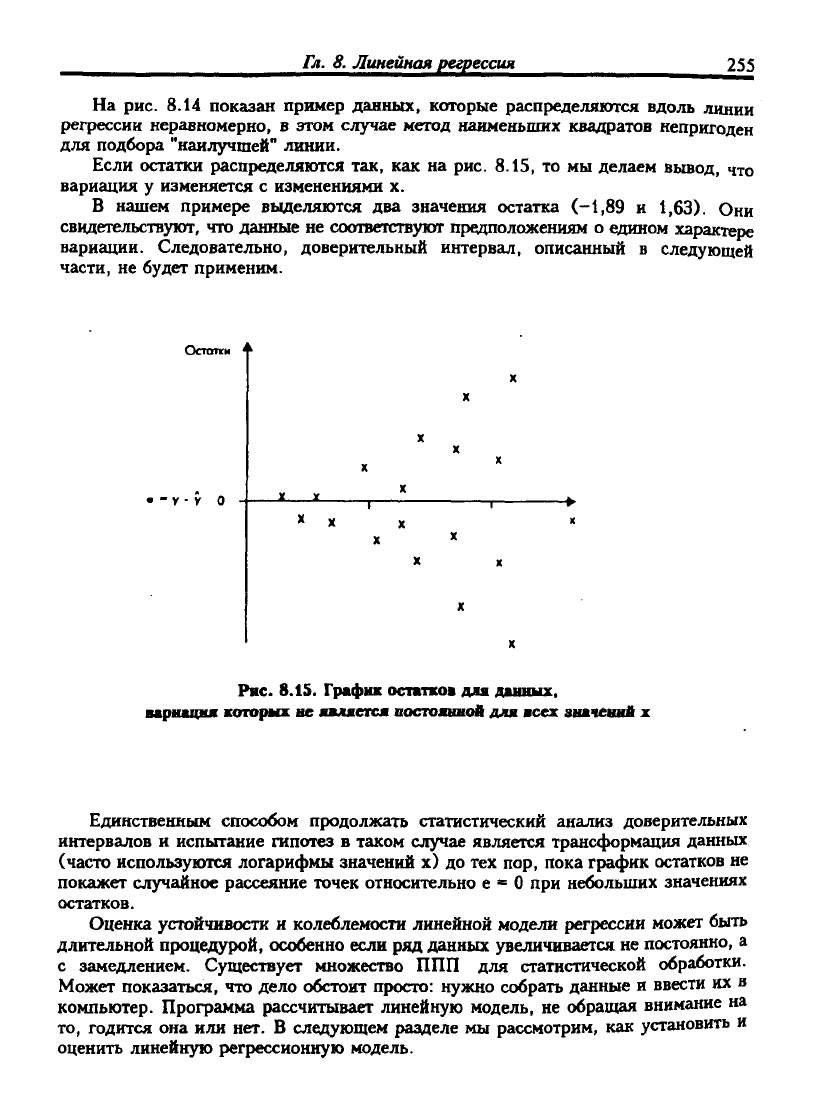
Если остатки распределяются так, как на рис. 8.15, то мы делаем вывод, что

вариация у изменяется с изменениями х.

В нашем примере выделяются два значения остатка (-1,89 и 1,63). Они

свидетельствуют, что данные не соответствуют предположениям о едином характере

вариации. Следовательно, доверительный интервал, описанный в следующей

части, не будет применим.

Остопси

• - у - у о

X X

Рис. 8.15. График остатков для данных,

вариация которых ве является востояниой для всех значений х

Единственным способом продолжать статистический анализ доверительных

интервалов и испытание гипотез в таком случае является трансформация данных

(часто используются логарифмы значений х) до тех пор, пока график остатков не

покажет случайное рассеяние точек относительно е =

при небольших значениях

остатков.

Оценка устойчивости и колеблемости линейной модели регрессии может быть

длительной процедурой, особенно если ряд данных увеличивается не постоянно, а

с замедлением. Существует множество ППП для статистической обработки.

Может показаться, что дело обстоит просто: нужно собрать данные и ввести их в

компьютер. Программа рассчитывает линейную модель, не обращая внимание на

то,

годится она или нет. В следующем разделе мы рассмотрим, как установить и

оценить линейную регрессионную модель.

256 4.2.

Анализ данных

как

составная часть принятия решений

8.5. СТАТИСТИЧЕСКИЙ ВЫВОД В АНАЛИЗЕ

ЛИНЕЙНОЙ РЕГРЕССИИ

8.5.1.

Основные предпосылки

В этом разделе мы обсудим одно из обязательных предположений, лежащих в

основе дальнейшего анализа линейной регрессионной модели. Данные, по кото-

рым построена модель линейной регрессии, являются выборкой пар значений х и

у. В сущности, мы используем выборку для построения модели, которая в общем

виде представит связь. Связь между зависимой переменной у и независимой

переменной х описывается как:

у = о + Рх + е,

где

Б —

отклонение от значения у на линии:

у = о

Рх.

Для данного значения х: у = а + рх — линейная модель, которую можно

построить, имея все необходимые данные.

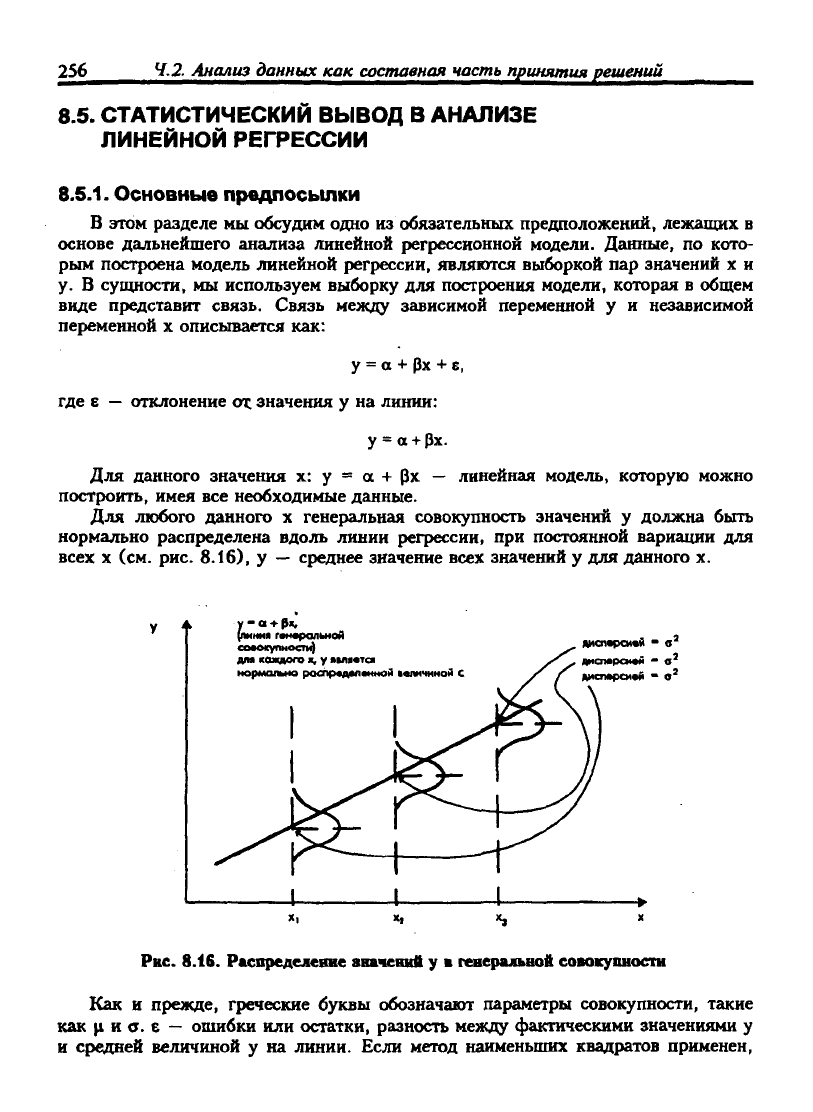
Для любого данного х генеральная совокупность значений у должна быть

нормально распределена вдоль линии регрессии, при постоянной вариации для

всех

(см. рис. 8.16), у

—

среднее значение всех значений у для данного х.

-о»

-о'

.-2

Рис. 8.16. Расвредеяевие ашчений у

генералыюй совокупиости

Как и прежде, греческие буквы обозначают параметры совокупности, такие

как ц и о. е

—

ошибки или остатки, разность между фактическими значениями у

и средней величиной у на линии. Если метод наименьших квадратов применен,

Гл.

8. Линейная

регрессия

257

чтобы получить линию, которая была наиболее подходящей к данным, то это

может быть достигн)гго, если мы минимизируем J] е^. Линейная модель, которую

мы вычисляем по выборке, имеет вид:

у =

а + Ьх,

где

у —

оценка генеральной средней у для данного значения х, а и b

—

выборочные

оценки параметров генеральной совокупности а и р.

Как в любом случае, если мы произведем вторую выборку, значения а и b

буд)т другими. Существует аналогия между использованием х для оценки ц и

использованием а для оценки а. Делая предположение относительно выборочного

распределении х, мы находим доверительный интервал для величины генеральной

средней ц.

Точно такая же процедура может бьггь использована для получения аир путем

вывода выборочных величин а и Ь. Нашей основной моделью является:

у = о +

Рх

+ е.

Предположения:

Связь является линейной;

Независимая переменная х предполагается известной и может быть исполь-

зована для прогноза у;

Ошибки, или остатки

Б,

нормально распределены;

Для любых данных х ожидаемое значение е равно О, т.е. Е (е)=0;

Дисперсия постоянна для всех значений х, т.е. дисперсия 8=сГ;

6. Ошибки независимы.

Если придерживаться этих предположений, то распределение значений у в

генеральной совокупности для данного х является нормальным со средней:

йу/х=а + Эх.

где

.^ обозначает среднее у для данного х при дисперсии, равной а

Линия регрессии, построенная по выборочным данным, является лучшей

оценкой линии генеральной совокупности, с а

—

лучшей оценкой а и b

—

лучшей

оценкой р. Так как существует множество всевозможных выборок, которые могут

бьггь произведены из данной генеральной совокупности, нельзя быть уверенным,

что эта выборка произведена именно из данной генеральной совокупности. Должно

бьггь проведено испытание гипотез по данным выборки для того, чтобы установить

соответствие выборки генеральной совокупности. Прежде всего, насколько уверенно

мы можем говорить о линейной связи в исходной совокупности. Если в совокуп-

ности линейная связь отсутствует, то коэффициент корреляции генеральной сово-

купности р будет равен нулю и Р — показатель наклона линии регрессии также

будет равен нулю. До проверки линейности нам необходимо вычислить довери-

тельные интервалы для показателя наклона р, точки пересечения а, при среднем

значении у для данного х или при индивидуальном значении у для данного х. Как

и в предыдущих главах, будем использовать случайную выборку для расчета

выборочных статистик и для оценки соответствующих параметров совокупности.

258 4.2.

Анализ данных

как

составная часть пршштия решений

8.5.2. Испытание гипотезы для оценки линейности связи

Воспользуемся данными случайной выборки из генеральной совокупности для

измерения линейной связи для совокупности. Мы не знаем, является ли связь в

генеральной совокупности линейной. Случайная выборка может свидетельство-

вать о линейности связи переменных, тогда как в действительности в генеральной

совокупности связь может быть нелинейной. Такого рода возможности показаны

на рис. 8.17 и 8.18.

. о

о *

о о . • .•

. '• • о Выборочный

' о . домны»

. • на софокупностм

. О

Рнс. 8.17. Случайная ммборка Рис. 8.18. Случайная выборка

из генеральной еовокупностн, с нелинейной связью

с линейной связью

Необходимо установить вероятность того, что линейная связь в выборочной

совокупности свидетельствует о линейной связи в генеральной совокупности. В

решении этой задачи нам поможет испытание гипотезы. Как

любой ситуации, где

используются гипотезы, мы не можем без сомнения утверждать, что связь в

генеральной совокупности совместима со связью в выборочной совокупности.

Определим совместимость через испытание нулевой гипотезы. Линейная регрессия

отображается в нескольких статистиках и можно провести проверку гипотезы для

каждой из них, а потом сделать совокупный вывод. Нулевые гипотезы при этом

формируются аналогично вышеуказанным. В данном случае нулевая гипотеза

означает отсутствие линейной связи между зависимой и независимой переменными

в генеральной совокупности.

КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ В ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ р

Вычисление коэффициента корреляции Пирсона зависит от размера выборки.

Если мы интерпретируем величину г с точки зрения выборки, то не принимаем во

внимание ее размер. Вывод о связи

генеральной совокупности зависит от размера

выборочной

совокупности.

Так,

если мы

по/^чили коэффициент корреляции, например

0,90, который рассчитан для выборочной совокупности из шести единиц, и сравнива-

ем его с таким же значением, которое было рассчитано для совокупности из

двадцати единиц, то во втором случае мы более уверены, что связь в генеральной

Гл.

8. Линейная

регрессия

259

совокупности

—

линейная. Шанс получения выборочной совокупности, в которой

связь линейна, из генеральной совокупности, в которой связь не линейна, умень-

шается по мере увеличения размера выборки. Коэффициент корреляции оценива-

ется с помощью t-критерия:

HQ:

Между переменными х и у не существует линейной связи, иначе говоря,

независимая переменная х не помогает в предсказании значений у, т.е. р=0.

Hj:

р * О, т.е. между переменными х и у существует некая линейная связь, х

помогает в прогнозировании у.

Используя эти альтернативные гипотезы, мы получим двусторонний критерий.

Если бы мы решили, что р должна

быть

только положительным, то Н^: р>0 и мы

использовали бы односторонний критерий:

лГ^

(1 - гЪ

Количество степеней свободы равно (п-2), так как мы рассчитали х и у для

нахождения г, используя две степени свободы, п

—

число пар значений выборки.

Если бы нам понадобилось провести испытание при

5%-ном

уровне значимости,

используя двусторонний критерий, полученное значение критерия нужно сравнить

с to_o25,(n-2) ""3 Приложения 2.

Для того чтобы проиллюстрировать наши действия, вернемся к примеру 8.1.

Мы получили значение коэффициента корреляции

1=0,958.

Тогда значение критерия:

,.^1Ж4.лга|-9,45.

(1 -

0,958^)

0,082

Количество степеней свободы: (10-2) = 8

По таблицам Приложения 2 находим: tg

025,8

~ 2,306.

Рассчитанное значение критерия (9,45) оольше, чем 2,306. Поэтому мы отверг-

нем Но на

5%-ном

уровне значимости и выберем гипотезу Hj, т.е. мы в праве

предположить, что коэффициент корреляции в генеральной совокупности не равен

нулю,

и что между временем и расстоянием существует линейная связь. Этот

результат можно было предвидеть, учитывая высокое значение коэффициента

корреляции г.

КРИТЕРИЙ ПРОВЕРКИ ГИПОТЕЗЫ О СВЯЗИ НА ОСНОВЕ ПОКАЗАТЕЛЯ

НАКЛОНА ЛИНИИ РЕГРЕССИИ

В простой линейной регрессии критерий показателя наклона — коэффициента

регрессии, выполняет те же функции, что и критерий коэффициента корреляции.

Поэтому мы проводим либо испытание г, либо Ь, но не оба сразу. В уравнении

множественной регрессии, где имеется коэффициент регрессии для каждой неза-

висимой переменной, необходимы оба критерия, и они выполняют различные

функции.

HQ:

Между переменными нет линейной связи и х не помогает в прогнозе у,

т.е.

р=0.

260 4.2.

Анализ данных

как

составная часть принятия решений

Н^:

«^

О, т.е. существует линейная связь, и х помогает в прогнозе у.

В этом случае используют двусторонний критерий. Однако как и при испыта-

нии г, мы можем заменить этот критерий на односторонний, если предполагаем,

что Р>0 или р<0 — более значимые гипотезы. Формула критерия похожа на ту,

что мы использовали для ц и р в гл.6. Когда дисперсия генеральной совокупности

неизвестна, тестовая статистика для выборочной средней определяется как:

(выборочная статистика - параметр, предполагаемый

гипотезе Нд) ^ - ц)

наилучшая оценка стандартной ошибки статистики s/V

- 1'

Тестовая статистика для коэффициента регрессии Ь:

Ь-0

оцененная стандартная ошибка Ь'

Оцененная стандартная ошибка Ь:

^ь'

Vl(x-x)^

где а^

—

дисперсия распределения остатков вдоль линии регрессии генеральной

совокупности. Предположим, что дисперсия одинакова для всех значений х.

Лучшей оценкой генеральной дисперсии ст^ является:

°= "(11-2)° (п-2) •

Алгебраически это можно выразить как:

dy^-aXy-b^xy)

(п-2)

Чтобы проиллюстрировать наши действия, вернемся к примеру 8.1 о времени

и расстоянии. Используем первое выражение для о^:

2 0,78^

0,71^

... (-0,82)^ 10,01 . ,.

Поэтому

0Ге^=

1,12

мин.

и VS(x-5E)^=V(Sx^-^)

ViI

889 - 3,99,

Гл.

8. Линейная регрессия

Отсюда: 5еь-|^ 0,281.

Значение критерия для Р:

* 0,281 ^•*'-

Если принять допустимые погрешности, то с учетом округления значение 11

же,

как и значение t для коэффициента корреляции: 9,47 по сравнению с 9,4

Чтобы вычислить двусторонний критерий на

5%-ном

уровне, сравним знач

данного критерия со значением из Приложения 2:

to,025.8 ~ 2,306.

Так как 9,47 > 2,306, отвергнем гипотезу Но и принимаем гипотезу Hi

5%-ном

уровне принятия решения с ошибкой доказательство будет непосле;

тельным при наличии только нулевых гипотез. Таким образом, мы приш,

такому же выводу, что и ранее. Мы выбрали предположение, что сущеа

линейная связь между временем и расстоянием, т.е. р * О, х помогает объяс;

варьируемость признака у.

8.5.3. Доверительный интервал в линейном рвфессионном анали

ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ НАКЛОНА ЛИНИИ РЕГРЕССИИ!

Доверительный интервал (1-р) 100% для показателя наклона Р опредг

пределы значений Ь с ошибкой выборки р, в которых с вероягаостью (1-р) • 100 i^

дится р. Другими словами, для (1-р) • 100% выборок истинное значение р t

лежать в данном доверительном интервале. Доверительный интервал имеет тс

вид,

что и т е , которые рассматривались в гл. 5;

+ t (р/2)

(п-2) •

SCb-

Из вышеизложенного мы знаем, что:

set-

VX(x-50^ '

Рассчитаем 95%-ный доверительный интервал для наклона линии регрес»

примере 8.1 о времени и расстоянии поставок:

b ± Ц,_о25.8 scb = 2,66 + 2,31

•

0,281 = 2,66 + 0,65.

С вероятностью 95% мы можем сказать, что значения Р лежат между *_^

3,31 мин на милю; и 5% — вероятность того, что значение Р лежит вне дат

интервала.

262 4.2.

Анализ данных

как

составная часть принятия решений

ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ у ПРИ

ДАННОМ ЗНАЧЕНИИ X

Теперь вернемся к основному предположению о том, что для данного значения х,

обозначим его х^, возможные значения у нормально распределены. Среднее

значение этих нормальных распределений — значение у на линии регрессии

генеральной совокупности. Обозначим среднее значение ц^ Доверительный ин-

тервал для \1,: с вероятностью (1-р) • 100 имеет вид: "^

где у

—

оцененное значение у, вычисленное из выборочной регрессии у = а + Ьх.

Заметим, что доверительный интервал зависит от значения

XQ.

Поэтому шири-

на интервала варьирует по мере изменения х. Интервал является наименьшим,

когда хо = X. В этом случае интервал примет более знакомый нам вид:

Ширина интервала растет по мере того, как увеличивается отличие хо от х в

любом направлении.

В примере 8.1 при вероятности

95%

доверительный интервал

liyj^^

равен:

л . ./1

(Хо

- 2,89)''

где:

у = 5,91 + 2,66 х^.

Значения для этого интервала будут вычислены в следующем разделе.

ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ ИНДИВИДУАЛЬНЫХ ЗНАЧЕНИЙ у

ПРИ ДАННОМ ЗНАЧЕНИЯ х

Остановимся на следующем предположении для данной модели, что значения у

распределены вдоль линии регрессии с вариацией

а^

, которая одинакова для всех

значений х. Так как мы используем выборку, то существуют два элемента изменя-

емости признака у. Один исходит из оцененной позиции математического ожида-

ния (среднего) ц,, а другой — из отклонений индивидуальных значений от

своего среднего значения.

Эти два элемента различны: во-первых, благодаря колебаниям внутри выбор-

ки,

которые могут быть сокращены, если увеличится размер выборки; во-вторых,

благодаря природе переменных эти колебания неизбежны. Поэтому утверждать

доверительный интервал для индивидуальных значений у не похож на другие

доверительные интервалы, которые полностью подвержены эффекту выборочных

колебаний. Некоторые исследователи считают их интервалами 4прогноза», а не

доверительными интервалами. Но как бы их ни называли, важно понять различие

между (1-р) 100%, интервалом для \^у/х и интервалом для индивидуальных

значений у при данном х.